🍤 💥 🏻 3d图形中的样条线，最自动化的选项 ⛷️ 👺 👩🏿‍🎓

大约一个月前，我开始从Dawson的书中学习Python，并在pygame下编写游戏的过程中深深地醒了过来。 TK如此看来，通过将保存的3d样条曲线的表面填充到子图形中来制作具有伪三维图形的游戏似乎是最有前途的。我将写后者。

因此，有一些多边形（最容易使用四边形）要在其上拉伸三次曲面，以使它们非常平滑地配合在一起-这些曲面是样条曲线。

将一个多边形的样条曲线作为函数展示是最方便的

g （ u ， v ） = v c d o t g_{1} （ u ） + （ 1 - v ） c d o t g_{2} （ u ） + u c d o t g_{3} （ v ） + （ 1 - u ） c d o t g_{4} （ v ） （ 1 ）

$g（u，v）= v \ cdot g_1（u）+（1-v）\ cdot g_2（u）+ u \ cdot g_3（v）+（1-u）\ cdot g_4（v）（1）$

在这里

g_{1} ， g_{2} ， g_{3} ， g_{4}

$g_1，g_2，g_3，g_4$

-满足某些边界条件的三次多项式（在下图中-浅绿色和红色曲线，以及导数-初始条件-丁香和蓝色矢量）； u和v从0到1。

在这种解释中，会损失一些度数（参数2度和3度的乘积），但是可以通过仅指定12个初始条件向量（4个多边形点以及每个点相对于u和v的导数向量）来找到多项式的系数。在交界处，如果为相邻的多边形设置了相似的初始条件，则样条线会重合（导数向量必须是共线的，曲面会通过多边形的相同点）。

一个问题-在整个边界上都带有这种问题的陈述的派生词可能不一致-交界处会出现小的伪像。您可以再想出4个条件来更正此问题，然后在公式中仔细添加另一个术语

u c d o t v c d o t （ u - 1 ） c d o t （ v - 1 ） c d o t g_{5} （ u ， v ）

$u \ cdot v \ cdot（u-1）\ cdot（v-1）\ cdot g_5（u，v）$

不会破坏边界，但这是另一篇文章的主题。

一种替代方法是Bezier曲面，但它建议设置16个参数（对我而言）的数学含义是难以理解的，即假定艺术家将用自己的双手工作。这对我来说不太合适，因此带拐杖的自行车随之而来。

通过找到转角处的值和导数矩阵的逆矩阵，然后乘以输入条件（每个坐标三次），可以最容易地计算系数（1）。矩阵可以是这样的：

隐藏文字

[[1，0，0，0，0，0，0，0，0，0，0，0]，#g（0,0）
[1，0，0，0，1，0，0，0，1，0，1，0]，#g（1,0）
[1，1，1，1，0，0，0，0，0，0，0，0]，#g（0,1）
[1，1，1，1，1，1，1，1，1，1，1，1，1]，#g（1,1）
[0，0，0，0，1，0，0，0，0，0，0，0]，＃dg / du（0,0）
[0，0，0，0，1，0，0，0，2，0，3，0]，＃dg / du（1,0）
[0，0，0，0，1，1，1，1，0，0，0，0]，＃dg / du（0,1）
[0，0，0，0，1，1，1，1，2，2，3，3]，＃dg / du（1,1）
[0，1，0，0，0，0，0，0，0，0，0，0]，＃dg / dv（0,0）
[0，1，0，0，0，1，0，0，0，1，0，1]，＃dg / dv（1,0）
[0，1，2，3，0，0，0，0，0，0，0，0]，＃dg / dv（0,1）
[0，1，2，3，0，1，2，3，0，1，0，1]]＃dg / dv（1,1）

NumPy在这方面做得很好。

一个问题仍然存在-在哪里获得导数向量。假定必须基于相邻点（对于多边形）的位置以及出于平滑性的原因以某种方式选择它们。
就我个人而言，如何处理导数向量的长度仍然完全违反直觉。方向是可以理解的，但是长度呢？

结果，诞生了以下算法：

在第一阶段，会发生一些点分类。在图形中（多边形的点及其连接指定了点），搜索并存储了长度为4的循环，此外，还记录了最适合扩展多边形边缘作用的邻居（预先确定哪些边缘对应于参数u的变化，哪些边缘对应于v）。这是一段代码，用于搜索，排序和记住某个循环的第0点的邻居：

隐藏文字

"""   : cykle[5] cykle[7] cykle[4]--cykle[0] --u-- cykle[1]-cykle[6] |v |v cykle[10]-cykle[3] --u-- cykle[2]-cykle[8] cykle[11] cykle[9] """ sosed = [] for i in range(0, N): if self.connects[i][ind] == 1 and i != cykle[0] and i != cykle[1] and i != cykle[3]: sosed += [i] #    ... if(len(sosed) < 2): continue #    else: #      cykle[0] vs0c3 = MinusVecs(self.dots[sosed[0]], self.dots[cykle[3]]) vs1c1 = MinusVecs(self.dots[sosed[1]], self.dots[cykle[1]]) #        vs0c1 = MinusVecs(self.dots[sosed[0]], self.dots[cykle[1]]) vs1c3 = MinusVecs(self.dots[sosed[1]], self.dots[cykle[3]]) Rvsc = [ScalMult(vs0c3,vs0c3),ScalMult(vs1c1,vs1c1),ScalMult(vs0c1,vs0c1),ScalMult(vs1c3,vs1c3) ] n1 = Rvsc.index(max(Rvsc)) if n1 < 2: cykle += [sosed[1],sosed[0]] #  u   v else: cykle += [sosed[0],sosed[1]]

此外，在构建样条线时，将基于边缘的两个点和一个相邻点的位置（例如，点vec1，vec2和vec3;寻找导数的点是第二个点）来选择沿多边形点的边缘（例如，相对于参数u）的导数。

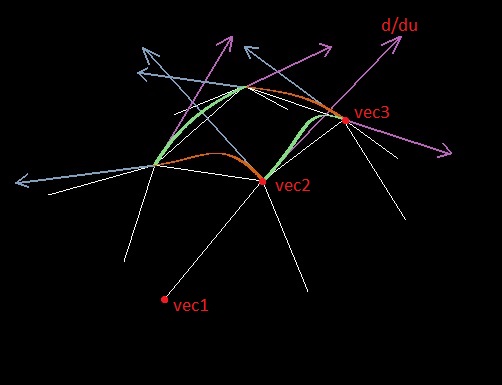
最初，我尝试使用归一化向量vec3-vec1（就像我应用拉格朗日定理一样）来实现这个角色，但是精确地导数向量的长度出现了问题-使它成为常数是一个坏主意。

抒情离题：

为了简要说明参数化版本中的导数向量，我们转向一个简单的二维类比-这是一段圆弧：

g （ u ） = （ R s i n （ u p i / 2 ） ， R c o s （ u p i / 2 ） ）

$g（u）=（Rsin（u \ pi / 2），Rcos（u \ pi / 2））$

g^{'} （ u ） = （ R p i / 2 c d o t c o s （ u p i / 2 ） ， - R p i / 2 c d o t s i n （ u p i / 2 ） ）

$g'（u）=（R \ pi / 2 \ cdot cos（u \ pi / 2），-R \ pi / 2 \ cdot sin（u \ pi / 2））$

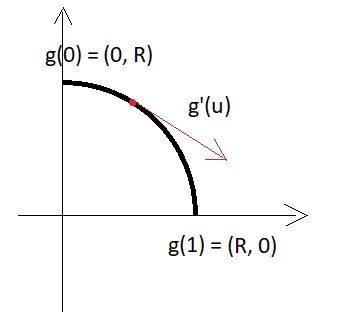
即微分模量= R * pi / 2，通常来说，取决于我们通过参数设置的弧段的大小。

现在该怎么办？列夫·尼古拉耶维奇·托尔斯泰（Leo Nikolaevich Tolstoy）向我们表示，一切都是圆形=良好，因此，如果将导数设置为好像我们要在此处建立圆弧的某个点，则将获得平滑的优美曲线。

离题的结尾。

导数搜索的第二阶段：

2.通过三个点vec1，vec2，vec3，我们构建了一个平面，在该平面中，我们寻找一个穿过所有三个点的圆。所需的导数将在点vec2处沿与圆的切线定向，并且导数的向量的模数应等于圆的半径和扇形角的乘积，后者形成多边形面的两个点（类似于我们从抒情性离题得出的简单平面类比）。

g^{'} = R c d o t p h i

$g'= R \ cdot \ phi$

一切似乎都很简单，例如，下面是功能代码（再次使用NumPy）：

不是代码，而是...

 def create_dd(vec1, vec2, tuda, vec3): """     1-2       3   == 1""" #0.         -         :( vecmult = VecMult(MinusVecs(vec2,vec1),MinusVecs(vec3,vec1)) #  vec2-vec1 x vec3 - vec1 if vecmult[0]*vecmult[0] + vecmult[1]*vecmult[1] + vecmult[2]*vecmult[2] < 0.000001: #  0 if tuda == 1: return NormVec(MinusVecs(vec3,vec2)) else: return NormVec(MinusVecs(vec1,vec2)) #1.   ,     #           2   M = np.zeros((3,3),float) C = np.zeros((3,1),float) M[0][0] = 2*vec2[0] - 2*vec1[0] M[0][1] = 2*vec2[1] - 2*vec1[1] M[0][2] = 2*vec2[2] - 2*vec1[2] C[0] = -vec1[0]*vec1[0] - vec1[1]*vec1[1] - vec1[2]*vec1[2] + vec2[0]*vec2[0] + vec2[1]*vec2[1] + vec2[2]*vec2[2] M[1][0] = 2*vec3[0] - 2*vec2[0] M[1][1] = 2*vec3[1] - 2*vec2[1] M[1][2] = 2*vec3[2] - 2*vec2[2] C[1] = -vec2[0]*vec2[0] - vec2[1]*vec2[1] - vec2[2]*vec2[2] + vec3[0]*vec3[0] + vec3[1]*vec3[1] + vec3[2]*vec3[2] #   ,   4     M[2][0] = vecmult[0] M[2][1] = vecmult[1] M[2][2] = vecmult[2] C[2] = vecmult[0]*vec1[0] + vecmult[1]*vec1[1] + vecmult[2]*vec1[2] # M *    = C Mobr = np.linalg.inv(M) Rvec = np.dot(Mobr,C) res = NormVec(VecMult(MinusVecs(Rvec,vec2), vecmult)) #    ka #R = math.sqrt((Rvec[0]-vec1[0])**2 + (Rvec[1]-vec1[1])**2 + (Rvec[2]-vec1[2])**2) #   = 3.14*2*asin(l/(2*R))/180 * R,      l  ,    l = 1.2*math.sqrt((vec1[0]-vec2[0])**2 + (vec1[1]-vec2[1])**2 + (vec1[2]-vec2[2])**2) if ScalMult(res, MinusVecs(vec2, vec1)) > 0: #     return MultVxC(res, tuda*l) else: return MultVxC(res, -tuda*l)

好吧，总的来说，这一切都可以。为了演示，我采用了一个5x5x5的立方体，并使用随机数发生器更改了点的位置：

GIF，8Mb

3d图形中的样条线，最自动化的选项

More articles: