为什么在简单的破碎机中需要C ++ 20的范围？

最近，已经在C ++ 20标准中讨论了很多范围，包括在Habré上（ 其中有很多示例 ）。 对间隔的批评家很多，他们说

• 它们太抽象了，只需要非常抽象的代码
• 代码对它们的可读性只会恶化
• 间隔减慢代码

让我们看完整 工农 实际任务，以便了解这种批评是否有效 的确是Eric Nibler被Bartosz Milewski咬伤，只在满月时才写range-v3 。

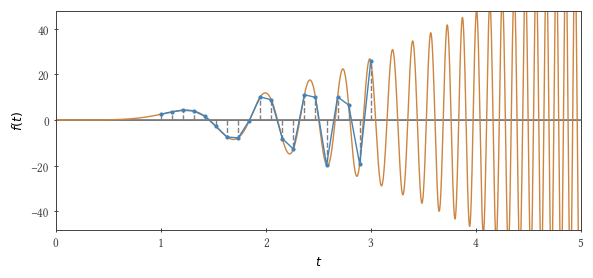
我们将使用梯形方法集成以下函数：$$ $内联$ f（t）= 3 t ^ 2 \ sin t ^ 3 $内联$ 从零到$$ $ inline $ \ tau $ inline $ 。 如果$$ $ inline $ \ tau ^ 3 / \ pi $ inline $ 等于奇数，则积分为2。

因此，问题来了：我们编写了一个函数的原型，该函数通过梯形方法计算积分。 乍看起来，这里不需要抽象，但是速度很重要。 实际上，这并非完全正确。 对于工作，我经常不得不写“数字粉碎机”，其主要用户是我自己。 因此，我还必须支持并处理他们的错误（不幸的是，我的同事们-并非总是我）。 而且还发生了一些代码未使用的情况，例如一年，然后……通常，还需要编写文档和测试。

积分器函数应具有哪些参数？ 可积分函数和网格（点集$$ $ inline $ t_1，t_2，t_3 ... $ inline $ 用于计算积分）。 并且，如果使用集成功能（ std::function就在这里）一切都清楚了，那么应该以哪种形式传输网格？ 让我们看看。

选件

首先-为了比较性能-我们将编写一个具有恒定时间步长的简单for循环：

 // trapezoidal rule of integration with fixed time step; // dt_fixed is the timestep; n_fixed is the number of steps double integrate() { double acc = 0; for(long long i = 1; i < n_fixed - 1; ++i) { double t = dt_fixed * static_cast<double>(i); acc += dt_fixed * f(t); } acc += 0.5 * dt_fixed * f(0); acc += 0.5 * dt_fixed * f(tau); return acc; } 

使用此循环时，可以将积分间隔的开始和结束以及积分本身的点数作为参数传递给函数。 停止-梯形方法也采用可变步长，而我们的可积函数只是要求使用可变步长！ 就是这样，让我们​​再增加一个参数（$$ $内联$ b $内联$ ）以控制“非线性”，并以以下步骤为例：$$ $ inline $ \ Delta t（t）= \ Delta t_0 + bt $ inline $ 。 这种方法（引入一个附加的数值参数）可能在百万个地方使用，尽管它的缺点似乎对每个人都显而易见。 如果我们有其他功能？ 如果我们需要在数值间隔的中间某个地方走一小步？ 但是，如果可集成函数具有几个功能，该怎么办？ 通常，我们必须能够传送任何网格。 （不过，在示例中，直到最后，我们将“忘记”真正的梯形方法，并且为简单起见，我们将以恒定的步长考虑其版本，并牢记网格可以是任意的）。

由于网格可以是任意网格，因此我们传递其值$$ $ inline $ t_1，t_2，... $ inline $ 包装在std::vector 。

 // trapezoidal rule of integration with fixed time step double integrate(vector<double> t_nodes) { double acc = 0; for(auto t: t_nodes) { acc += dt_fixed * f(t); } acc -= 0.5 * dt_fixed * f(0); acc -= 0.5 * dt_fixed * f(tau); return acc; } 

这种方法有足够多的社区，但是绩效呢？ 随着内存消耗？ 如果更早地将所有内容汇总在处理器上，那么现在我们必须先填充内存区域，然后再从中读取。 与内存的通信是一件相当缓慢的事情。 而且内存仍然不是橡胶（ 和有机硅 ）

让我们看一下问题的根源。 一个人需要什么才能快乐？ 更准确地说，我们的循环（基于范围的循环）需要什么？ 任何具有begin()和end()迭代器以及++ ， *和!=迭代器的运算符的容器。 所以我们会写。

 //   ,    ,      template <typename T> double integrate(T t_nodes) { double acc = 0; for(auto t: t_nodes) { acc += dt_fixed * f(t); } acc -= 0.5 * dt_fixed * f(0); acc -= 0.5 * dt_fixed * f(tau); return acc; } // ... //      class lazy_container { public: long long int n_nodes; lazy_container() { n_nodes = n_fixed; } ~lazy_container() {} class iterator { public: long long int i; // index of the current node iterator() { i = 0; } ~iterator() {} iterator& operator++() { i+= 1; return *this; } // ! bool operator!=(const iterator& rhs) const { return i != rhs.i; } double operator* () const { return dt_fixed * static_cast<double>(i); } }; iterator begin() { return iterator(); } iterator end() { iterator it; it.i = n_nodes; return it; } }; // ... //      lazy_container t_nodes; double res = integrate(t_nodes); 

我们在这里计算一个新值。$$ $内联$ t_i $内联$ 随需应变，就像我们在简单的for循环中所做的一样。 没有内存访问，希望现代编译器可以非常有效地简化代码。 同时，积分函数的代码变化不大，并且仍然可以消化std::vector 。

灵活性在哪里？ 实际上，我们现在可以在++运算符中编写任何函数。 即，实际上，该方法允许传递函数而不是单个数值参数。 动态生成的网格可以是任意网格，并且我们（可能）也不会失去性能。 但是，每次都写一个新的lazy_container只是以某种新方式扭曲网格根本感觉不到（这是27行！）。 当然，您可以将负责生成网格的函数作为我们集成函数的参数，并将lazy_container ，也就是说，对不起，将其封装起来。

您问-那么又会出问题了？ 是的 首先，有必要单独传输积分的点数，这可能会导致错误。 其次，所创建的非标准自行车将必须得到某人的支持和开发。 例如，您是否可以立即想象通过这种方法如何为++运算符中的函数组成一个组合器？

C ++已有30多年的历史了。 这个年龄的许多人已经有了孩子，而C ++甚至没有标准的惰性容器/迭代器。 一场噩梦！ 但是一切（从迭代器的角度来看，而不是从子类的角度来看）都将在明年改变-标准（可能是部分）将包括Eric Nibler几年来开发的range-v3库。 我们将使用其成果。 代码本身说明了一切：

 #include <range/v3/view/iota.hpp> #include <range/v3/view/transform.hpp> //... auto t_nodes = ranges::v3::iota_view(0, n_fixed) | ranges::v3::views::transform( [](long long i){ return dt_fixed * static_cast<double>(i); } ); double res = integrate(t_nodes); 

积分功能保持不变。 也就是说，仅3条线即可解决我们的问题！ 在这里， iota_view(0, n)生成一个惰性 间隔 （范围，一个封装了广义的begin和end的对象；惰性范围是一个视图），当在每个步骤中进行迭代时，该间隔将计算范围[0，n）中的下一个数字。 有趣的是，ι（希腊字母iota）这个名字在50年前就指的是 APL语言。 棒| 允许您编写间隔修饰符的管道，并且transform实际上是这样的修饰符，使用简单的lambda函数将整数序列变成一系列$$ $ inline $ t_1，t_2，... $ inline $ 。 一切都很简单，例如 童话 哈斯克尔。

但是如何进行可变步骤？ 一切都一样简单：

 #include <range/v3/view/drop.hpp> #include <range/v3/view/iota.hpp> #include <range/v3/view/transform.hpp> //... // trapezoidal rule of integration; step size is not fixed template <typename T> double integrate(T t_nodes) { double acc = 0; double t_prev = *(t_nodes.begin()); double f_prev = f(t_prev); for (auto t: t_nodes | ranges::v3::views::drop(1)) { double f_curr = f(t); acc += 0.5 * (t - t_prev) * (f_curr + f_prev); t_prev = t; f_prev = f_curr; } return acc; } //... auto step_f = [](long long i) { if (static_cast<double>(i) <= 1 / a) { return pow(2 * M_PI, 1/3.0) * a * static_cast<double>(i); } else { return tau * pow(static_cast<double>(i) / static_cast<double>(n), 1/3.0); } }; auto t_nodes = ranges::v3::iota_view(0, n) | ranges::v3::views::transform(step_f); double res = integrate(t_nodes); 

一位细心的读者注意到，在我们的示例中，可变步长使我们可以将网格点的数量减少三倍，同时，还有显着的计算开销$$ $内联$ t_i $内联$ 。 但是，如果我们采取另一个$$ $内联$ f（t）$内联$ ，积分的数量可能会发生更大的变化...（但是作者已经变得懒惰了）。

所以时机

我们有以下选择：

• v1-简单循环
• 第2版​​-$$ $内联$ t_i $内联$ 躺在std::vector
• lazy_container具有临时迭代器的临时lazy_container
• v4-C ++ 20的间隔（范围）
• v5-范围再次出现，但仅在此处使用可变音高编写梯形方法

这是结果（以秒为单位）$$ $ inline $ \ tau =（10 \，000 \，001 \ times \ pi）^ {1/3} $ inline $ ，适用于Intel®Xeon®CPU®X5550上的g ++ 8.3.0和clang ++ 8.0.0（步骤数约为$$ $内联$ 1.5 \乘以10 ^ 8 $内联$ ，但v5的步数减少了三倍（所有方法的计算结果与两者的相差不超过0.07）：

一般来说，苍蝇飞越田野，苍蝇找到了硬币！

总结

即使在一个非常简单的任务中，范围也被证明是非常有用的：我们编写了3行代码，而不是在20行以上带有自制迭代器的代码，而对代码的可读性或其性能没有任何问题。

当然，如果我们需要这些测试的最终性能，则必须通过编写并行代码（或在OpenCL下编写版本）来充分利用处理器和内存的资源。此外，我也不知道如果我编写很长的修饰符链。 在复杂项目中使用范围时，调试和读取编译器消息是否容易？ 会增加编译时间。 我希望有人写过这篇文章。

当我编写这些测试时，我本人不知道会发生什么。 现在我知道-在您打算使用它们的条件下，绝对值得在真实的项目中进行测试。

我去集市买了一个茶炊。

有用的链接

范围-v3主页

文档和案例研究v3

来自github上这篇文章的代码

haskell中的列表，以进行比较

致谢

感谢floydy帮助编写了所有这些内容！

聚苯乙烯

我希望有人对这种奇怪情况发表评论：i）如果您使积分间隔小10倍，那么在我的至强上，示例v2比v1快10％，而v4比v1快三倍。 ii）在这些示例中，有时英特尔编译器（icc 2019）生成的代码的速度是已编译g ++的两倍。 是归咎于矢量化吗？ g ++可以被迫做同样的事情吗？