功能依赖简介

在本文中，我们将讨论数据库中的功能依赖关系-它的含义，应用的位置以及用于搜索的算法。

我们将在关系数据库的上下文中考虑功能依赖性。 说得很不礼貌，在这样的数据库中信息是以表格的形式存储的。 此外，我们使用近似概念，在严格的关系理论中，这些近似概念是不可互换的：我们将表本身称为关系，列-属性（其集合-关系图）以及属性子集上的一组行值-元组。



例如，在上表中， （Benson，M，M organ ）是属性（Patient，Gender，Doctor）的元组。
更正式地说，其编写如下： $$$t_ {1}$[ 患者，保罗，医生 ] = （本森，男，男） 。
现在我们可以介绍功能依赖（FZ）的概念：

定义1. 关系R满足且仅当对于任何元组满足联邦法律X→Y（其中X，Y⊆R） $$$t_ {1}$， $$$t_ {2}$∈R成立：如果 $$$t_ {1}$[X] = $$$t_ {2}$[X]然后 $$$t_ {1}$[Y] = $$$t_ {2}$[Y]。 在这种情况下，可以说X（行列式或属性的定义集）在功能上定义了Y（从属集）。

换句话说，联邦法X→Y的存在意味着如果R中有两个元组并且它们在X的属性中重合，那么它们在Y的属性中也将重合。
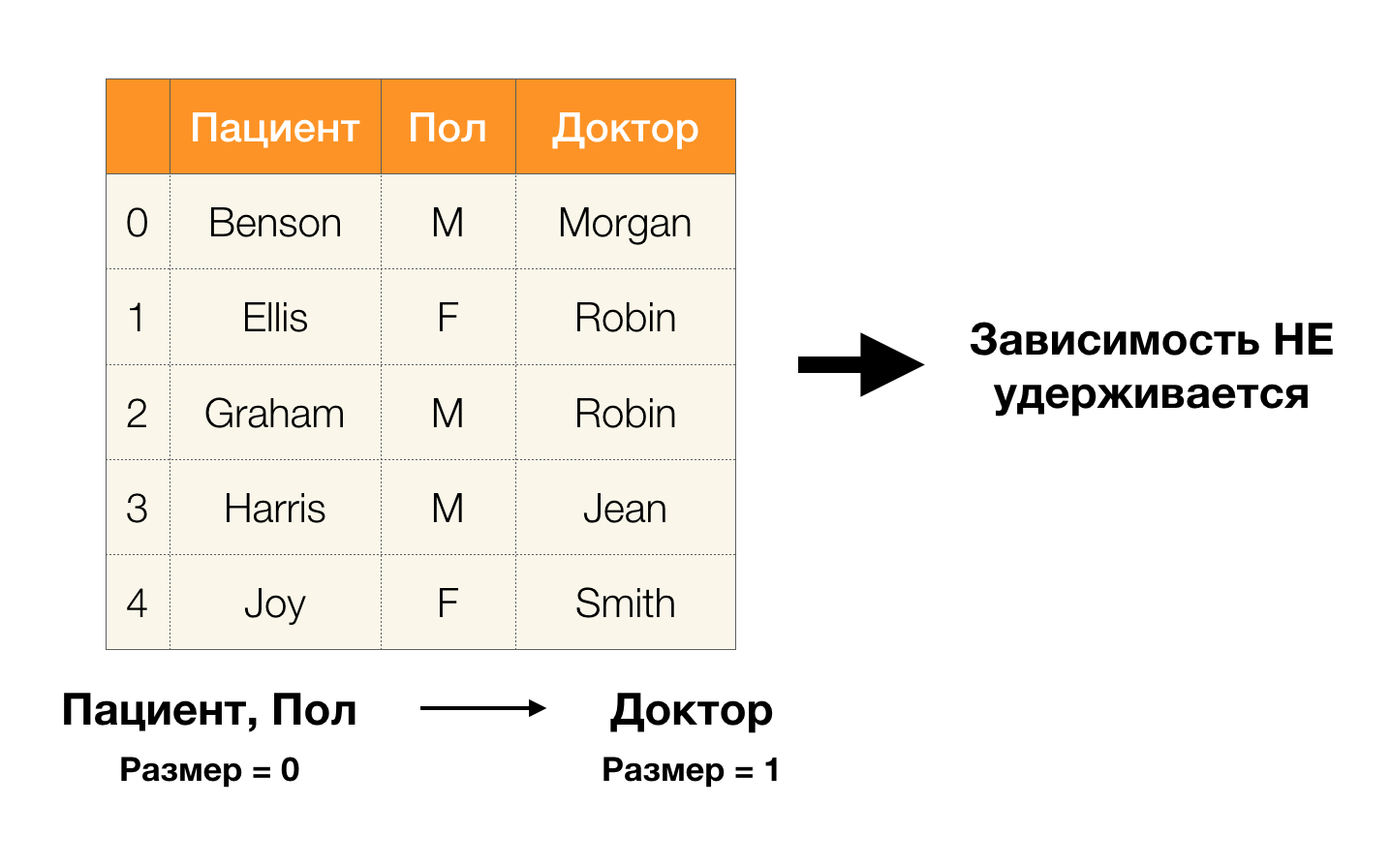
现在按顺序。 考虑一下我们想要查找其之间是否存在依赖关系的Patient和Gender属性。 对于这么多的属性，可能存在以下依赖关系：

1. 病人→性别
2. 性别→病人

根据上面的定义，为了保持第一依赖性，“ 性别”列中只有一个值必须与“ 患者”列中的每个唯一值相对应。 对于样本表，这是正确的。 但是，这在相反的方向上是行不通的，也就是说，不能满足第二个依赖性，并且Paul属性不是Patient的决定因素。 同样，如果您使用依赖关系Doctor→Patient ，则可以看到它被违反，因为此属性的Robin值具有几个不同的值-Ellis和Graham 。

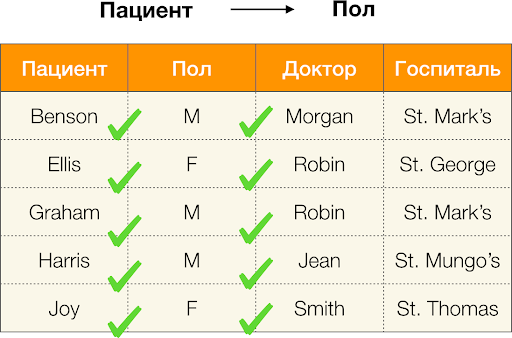
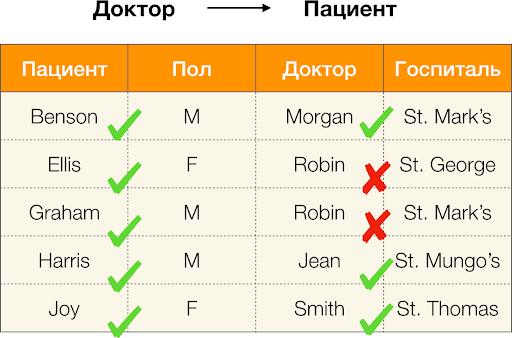
因此，功能依赖性使得确定表属性集合之间的现有关系成为可能。 从今以后，我们将考虑最有趣的关系，或者说X→Y使得它们是：

• 不平凡的，也就是说，依赖关系的右侧不是左侧的子集（Y̸⊆X） ；
• 极小，即没有Z→Y这样的依赖关系，使得Z Z X.

到目前为止，所考虑的依赖项是严格的，也就是说，它们在表上没有包含任何违规，但是除了它们之外，还存在那些允许元组的值之间存在一些不一致的行为。 这样的依赖关系放在一个单独的类中，称为“近似”，并允许在一定数量的元组上违反。 该数量由最大emax误差指示器调节。 例如比例误差 $$$e_ {max}$= 0.01可能意味着在所考虑的属性集上，可用元组的1％可能违反了依赖性。 也就是说，对于1000条记录，最多10个元组可能违反联邦法律。 我们将基于比较元组的成对差异值来考虑略有不同的指标。 对于X→Y对关系r的依赖性，认为如下：

$$

$$e（X \ rightarrow Y，r）= \ frac {| \ {（t_1，t_2）\ in r ^ 2 \ | | \ t_1 [X] = t_2 [X] \楔形t_1 [Y] \ neq t_2 [Y] \} |} {| r ^ 2 | -| r |}$$

我们根据上面的示例计算Doctor→Patient的错误。 我们有两个元组，其值在Patient属性上不同，但在Doctor上重合： $$$t_ {1}$[ 医生，病人 ] =（ 罗宾·埃利斯 ）和 $$$t_ {2}$[ 医生，病人 ] =（ 罗宾，格雷厄姆 ）。 按照错误的定义，我们必须考虑所有冲突对，这意味着将有两个： $$$t_ {1}$， $$$t_ {2}$）及其反演（ $$$t_ {2}$， $$$t_ {1}$） 代入公式并获得：

$$

$$\ frac {2} {5 ^ 2-5} = 0.1$$

现在，让我们尝试回答以下问题：“为什么要这么做？”。 实际上，联邦法律是不同的。 第一类是管理员在数据库设计阶段确定的依赖项。 通常它们很少，很严格，主要应用是数据规范化和关系方案的设计。

第二种类型是表示“隐藏”数据和属性之间先前未知关系的依赖关系。 也就是说，这种依赖性在设计时并未考虑，并且已经在现有数据集中找到，因此，基于已确定的联邦法律，可以得出有关存储信息的任何结论。 我们正在依靠这种依赖性。 他们使用基于其的各种搜索技术和算法来从事整个数据挖掘领域。 让我们了解在任何数据中找到的功能依赖性（精确或近似）如何有用。



如今，数据清理已成为依赖使用的主要领域之一。 它涉及识别“脏数据”及其后续纠正的过程的开发。 “脏数据”的鲜明代表是重复项，数据错误或错别字，缺失值，过时的数据，多余的空格等。

示例数据错误：



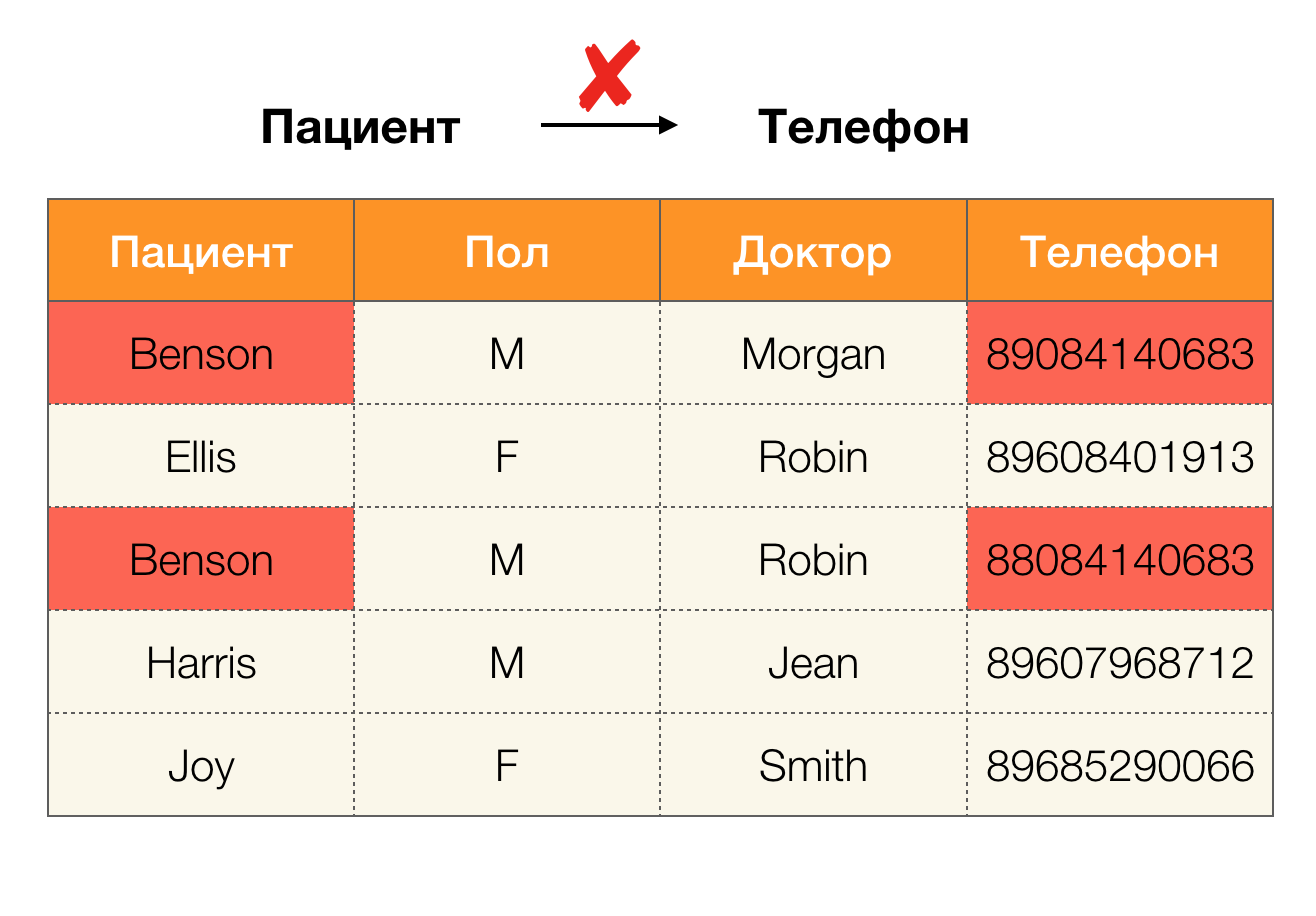
数据中的示例重复项：



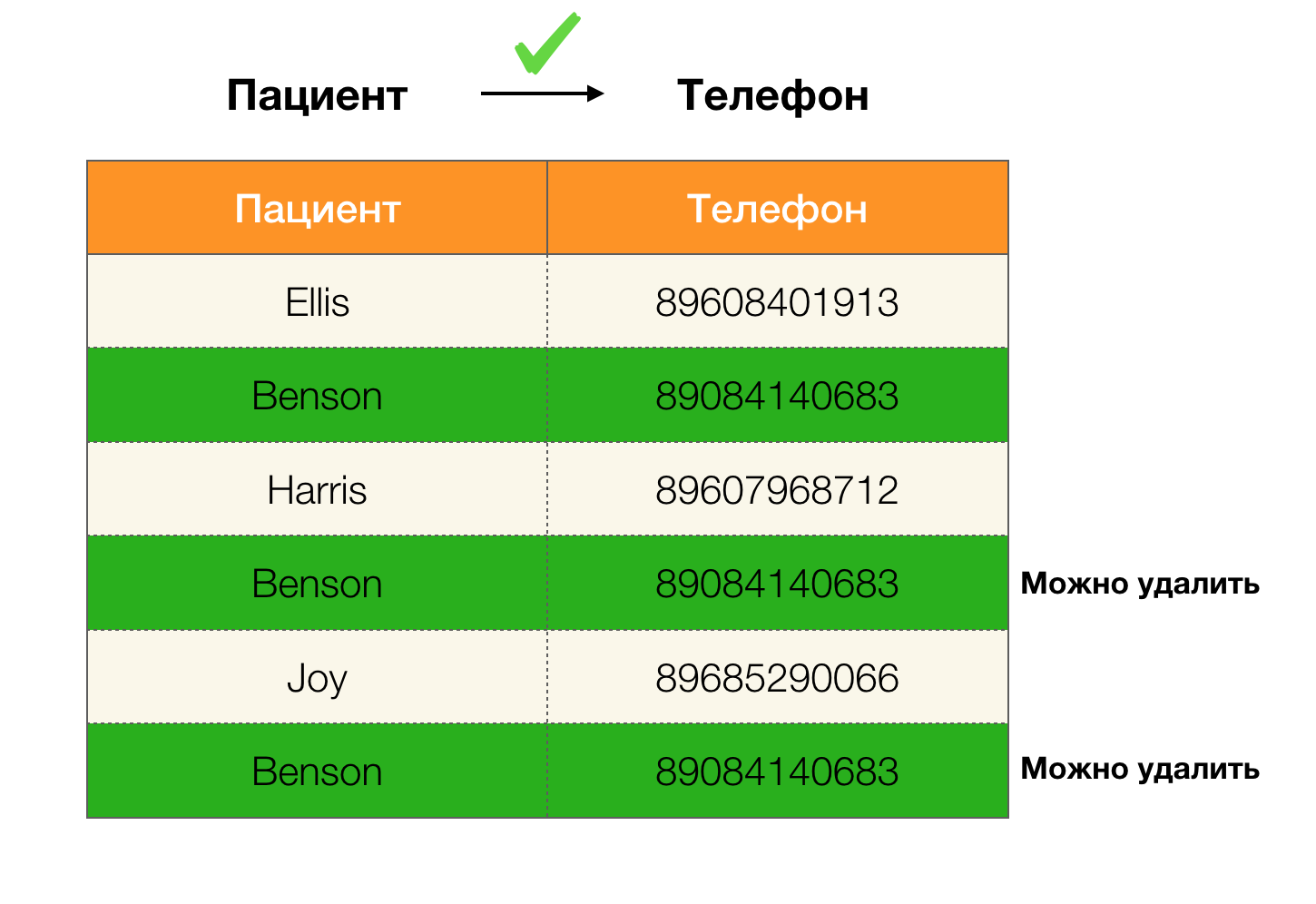
例如，我们有一个表和一组必须执行的联邦法律。 在这种情况下，数据清理涉及更改数据，以使联邦法律正确无误。 同时，修改的数量应该最少（对于此过程，本文中将不讨论某些算法）。 以下是这种数据转换的示例。 左边是初始关系，很显然，其中没有满足必要的联邦法律（用红色突出显示了违反其中一项联邦法律的示例）。 右侧是更新的关系，其中绿色单元格显示更改的值。 经过这样的过程，必要的依赖关系开始成立。



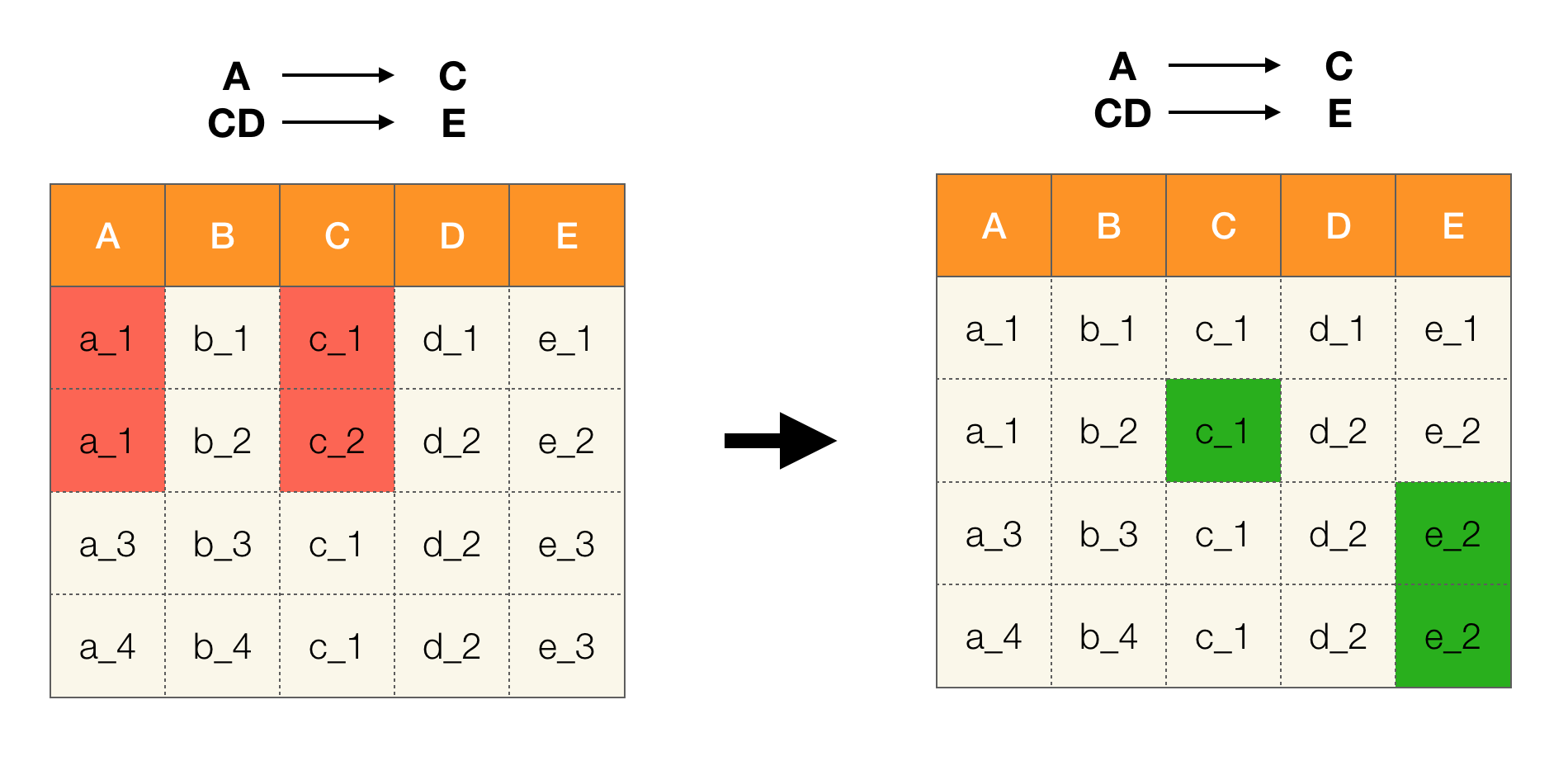
另一个流行的应用程序是数据库设计。 这里值得回顾一下范式和规范化。 规范化是使关系与一组特定要求保持一致的过程，每个要求均以自己的方式由范式确定。 我们不会写下各种标准格式的要求（这是数据库课程中任何针对初学者的书中所写的内容），但是我们仅注意到它们中的每一个都以自己的方式使用功能依赖的概念。 确实，联邦法律本质上是完整性约束，在设计数据库时会考虑到这些限制（在此任务的上下文中，有时将联邦法律称为超级密钥）。

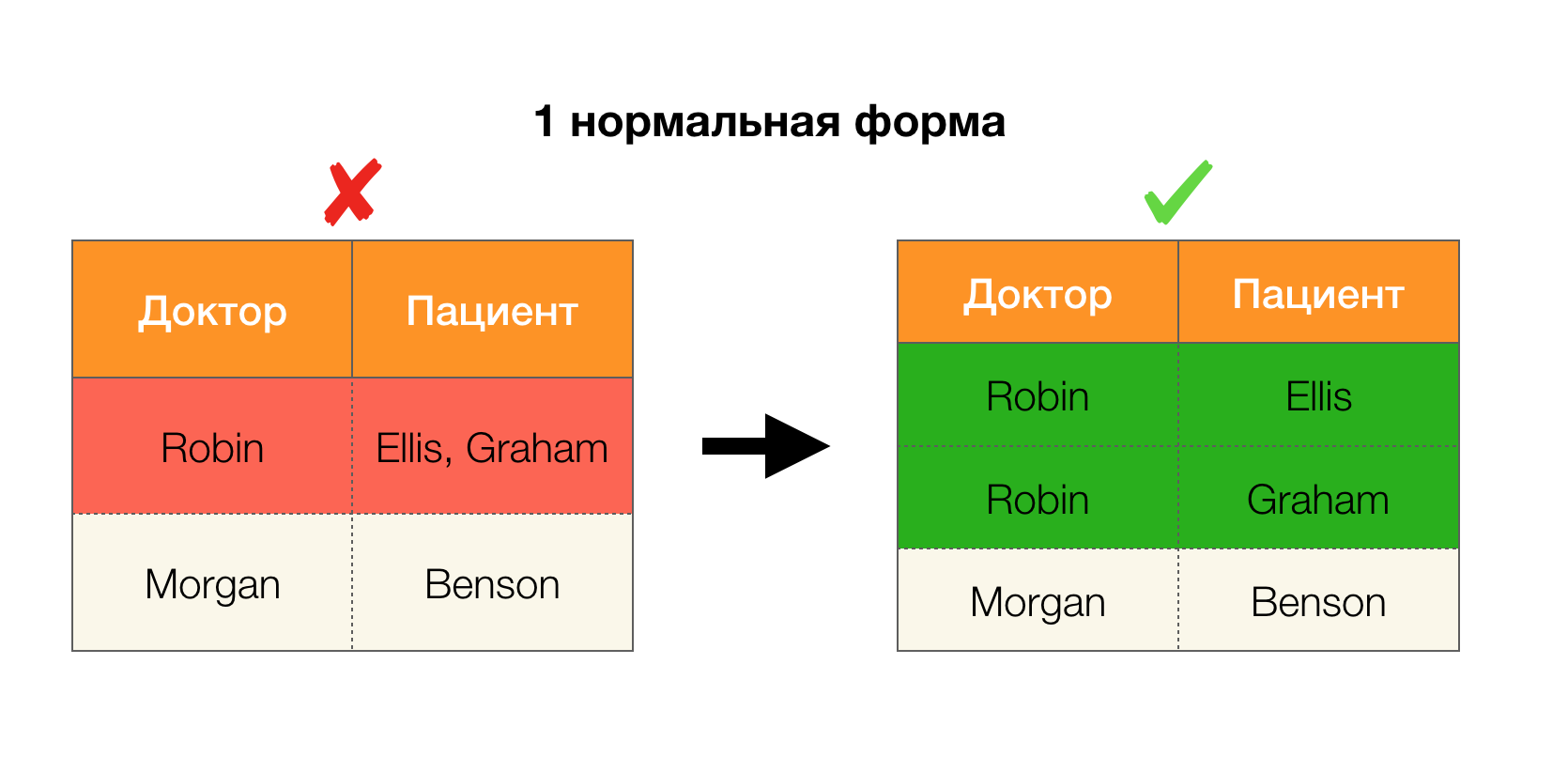
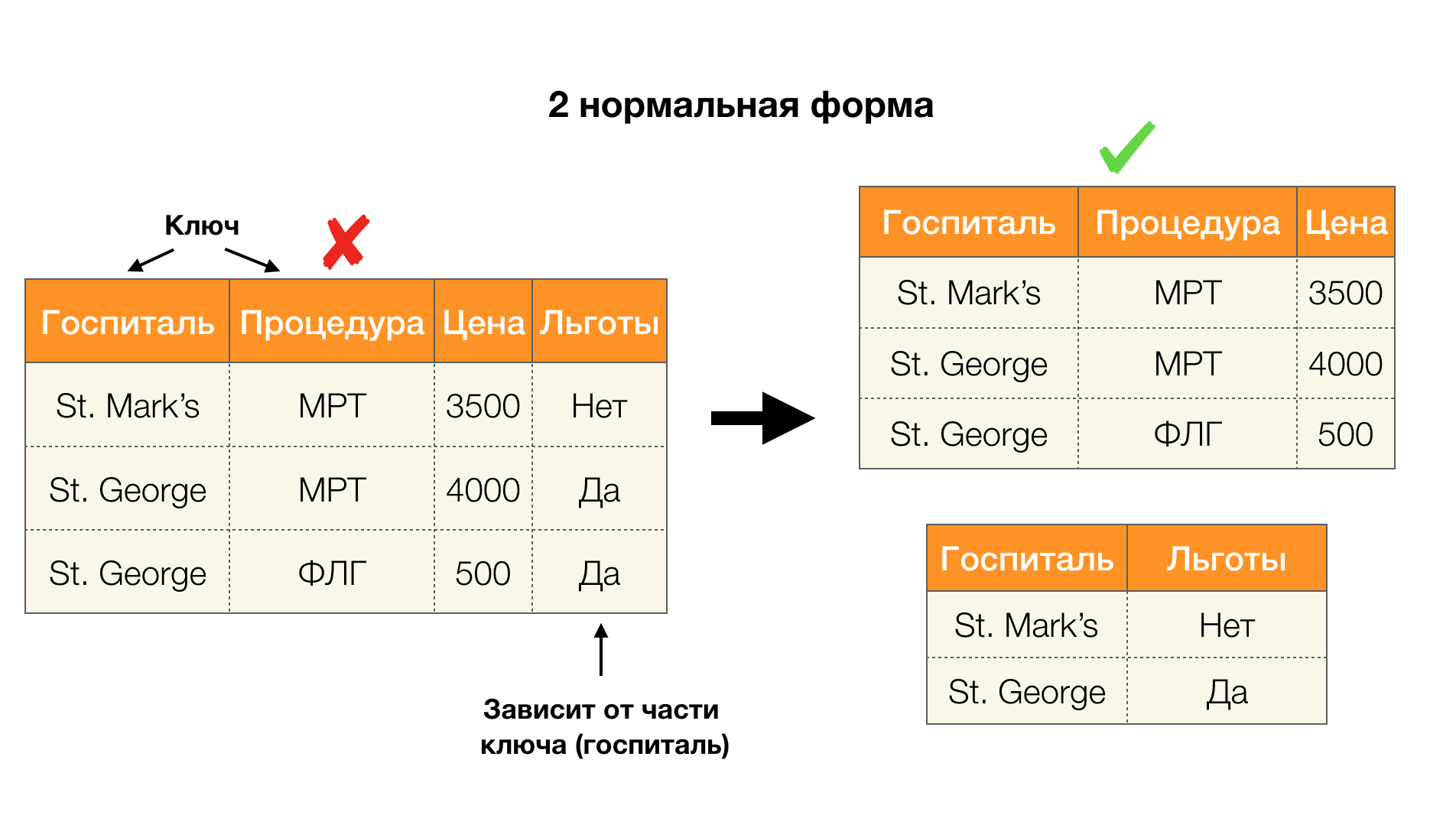
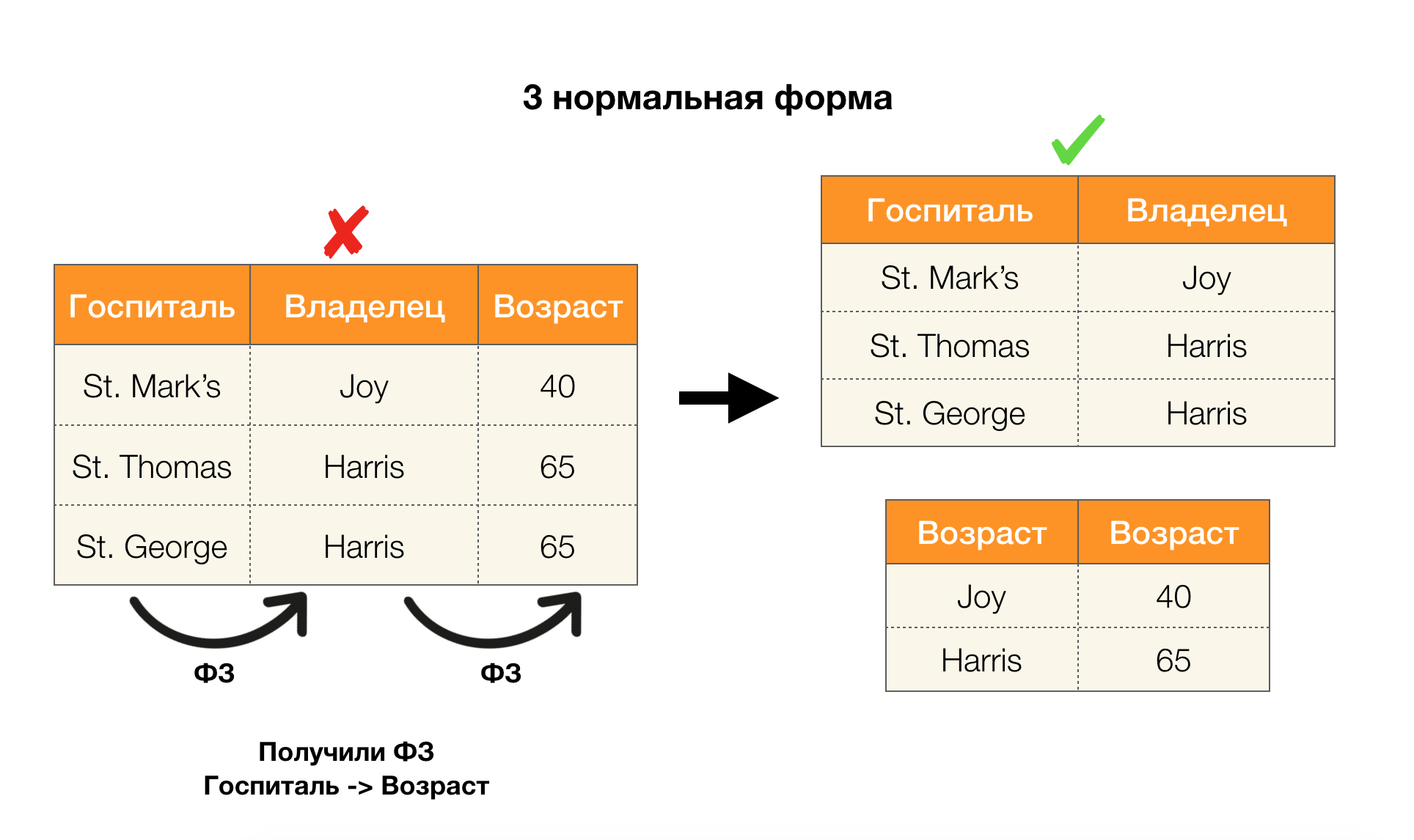
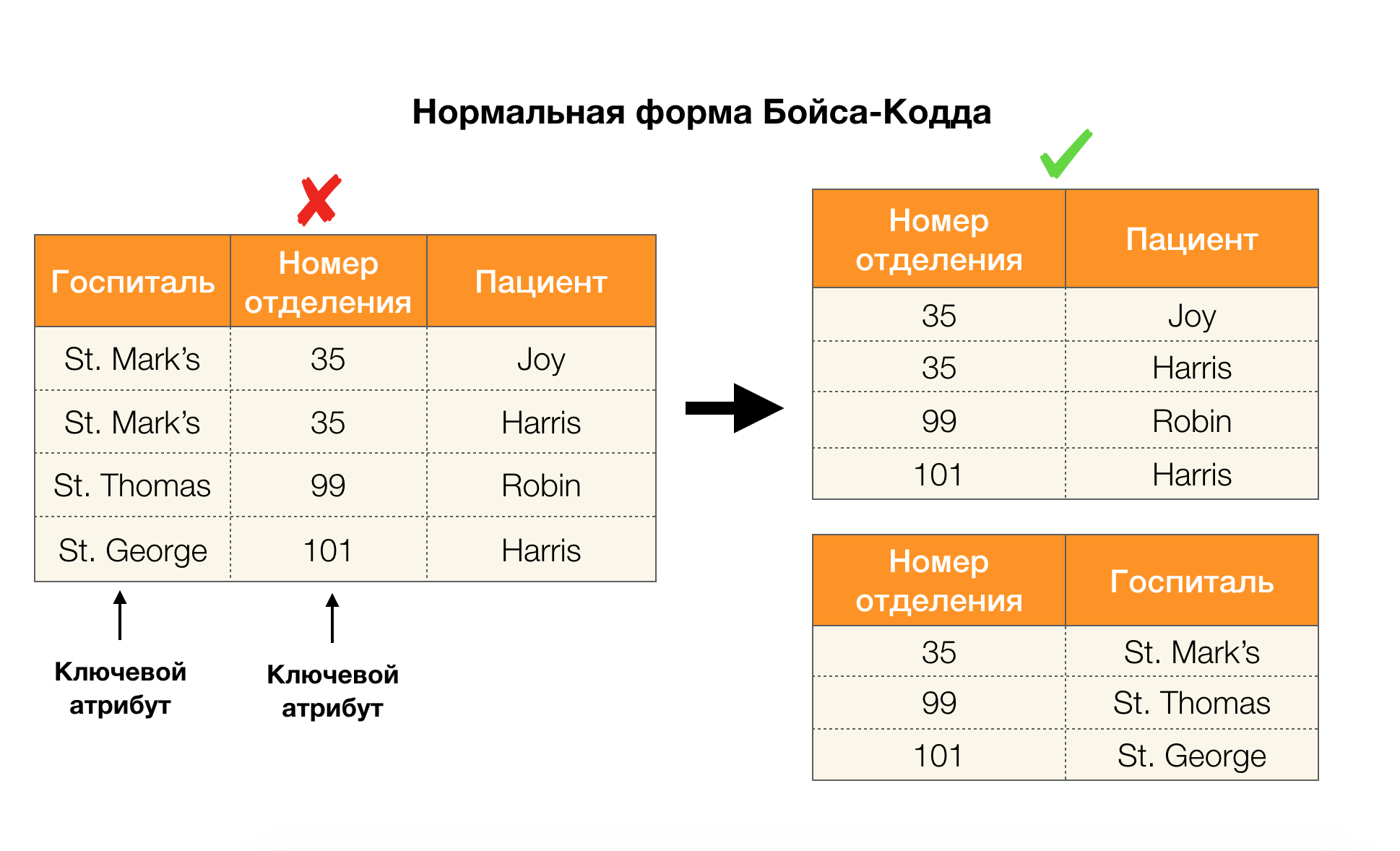
在下图中考虑它们对四种普通形式的应用。 回想一下，正常的Boyce-Codd形式比第三个形式更严格，但比第四个形式更不严格。 我们尚未考虑后者，因为它的表述需要了解多值依赖关系，本文对我们不感兴趣。






依赖关系已发现其应用的另一个领域是在诸如朴素贝叶斯分类器的构造，重要特征的标识以及回归模型的重新参数化等任务中，特征空间的尺寸减小。 在原始文章中，此问题称为冗余特征和特征相关性的确定[5，6]，并通过积极使用数据库概念来解决。 随着此类工作的到来，我们可以说今天需要一种解决方案，该解决方案允许将上述优化问题的数据库，分析和实现组合到一个工具中[7、8、9]。

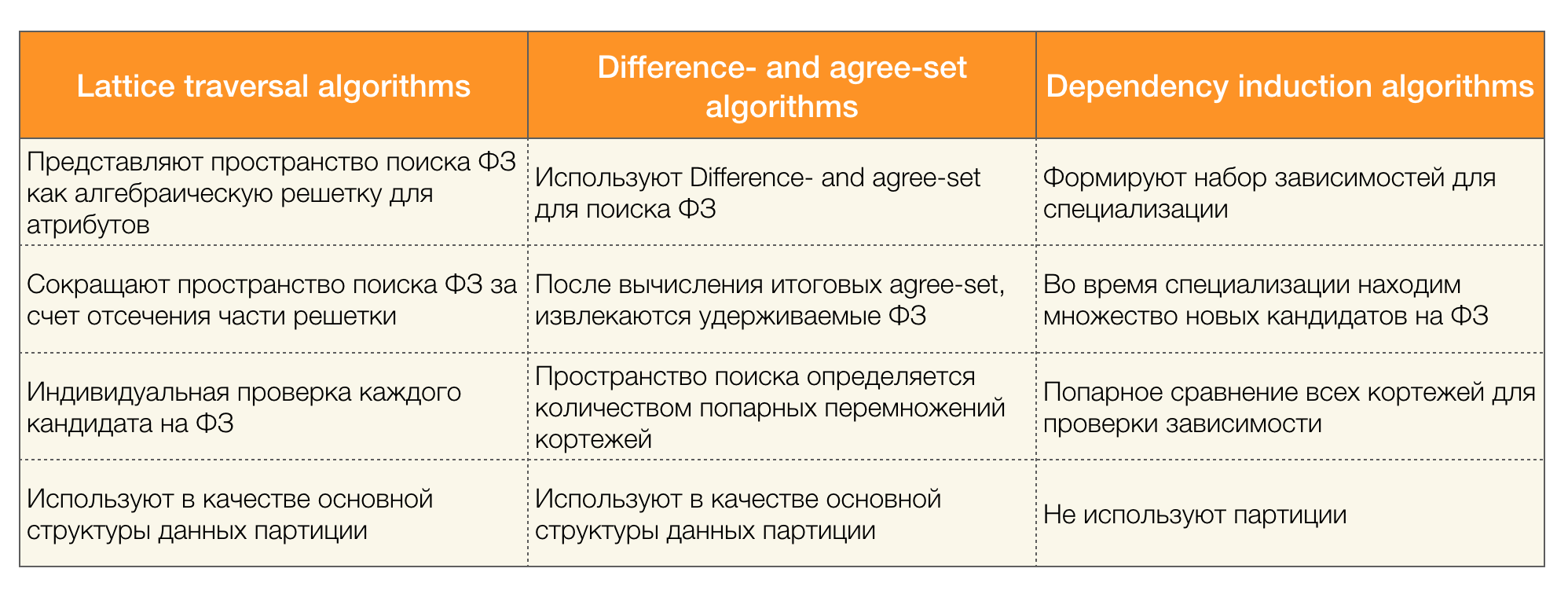
在数据集中搜索联邦法的算法有很多（现代的和不是很多种），这些算法可以分为三类：

• 使用代数格遍历的算法（格遍历算法）
• 基于搜索一致值的算法（差值和同意集算法）
• 成对比较算法（相关性归纳算法）
  

下表中简要介绍了每种算法：


关于这种分类的更多细节可以阅读[4]。 以下是每种类型的算法示例：





当前，出现了一种新算法，该算法结合了多种方法来一次搜索功能依赖性。 此类算法的示例为Pyro [2]和HyFD [3]。 在本系列的以下文章中，将对他们的工作进行分析。 在本文中，我们将仅分析了解理解依赖项检测技术所必需的基本概念和引理。

让我们从第二种算法中使用的简单的“差异和同意集”开始。 差异集是一组值不匹配的元组，相反，同意集是值匹配的元组。 应当指出，在这种情况下，我们仅考虑依赖关系的左侧。

上面遇到的另一个重要概念是代数格。 由于许多现代算法都在此概念上运行，因此我们需要对其概念有所了解。

为了介绍晶格的概念，有必要定义一个部分排序的集合（或简称为“ poset”的部分排序的集合）。

定义2。如果对于任何a，b，c∈S满足以下属性，则说集合S由二进制关系⩽部分排序：

1. 自反性，即a⩽a
2. 反对称，即如果a⩽b和b⩽a，则a = b
3. 传递性，即对于a b和b c，得出a c
   

这种关系称为（非严格）偏序关系，集合本身称为偏序集。 正式符号：⟨S，⩽⟩。

作为部分有序集的最简单示例，我们可以采用具有顺序usual的通常关系的所有自然数N的集合。 容易验证是否满足所有必需的公理。

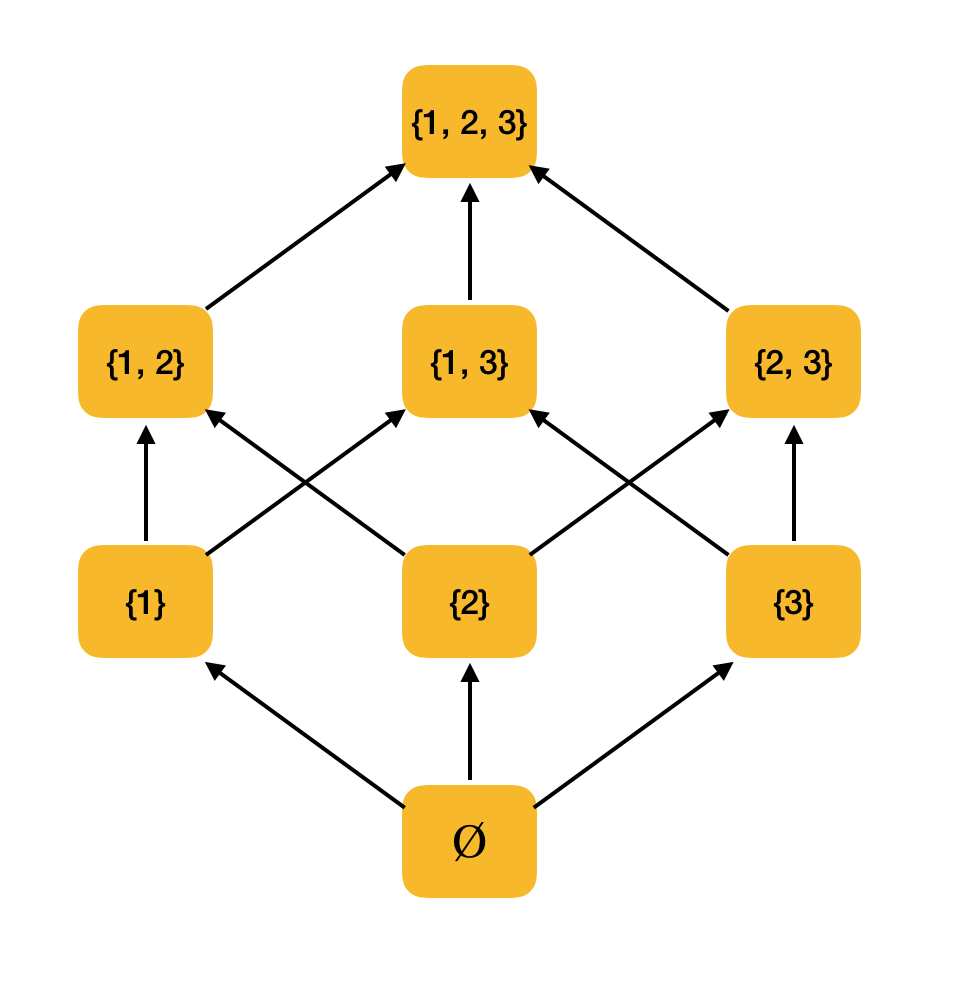
更有意义的例子。 考虑由包含关系ordered排序的所有子集{1、2、3}的集合。 实际上，该关系满足所有偏序条件；因此，; P（{1，2，3}），，是偏序集。 下图显示了此集合的结构：如果您可以从一个元素沿箭头移动到另一个元素，则它们与顺序有关。



我们将需要数学领域中的两个更简单的定义-最高和最低。

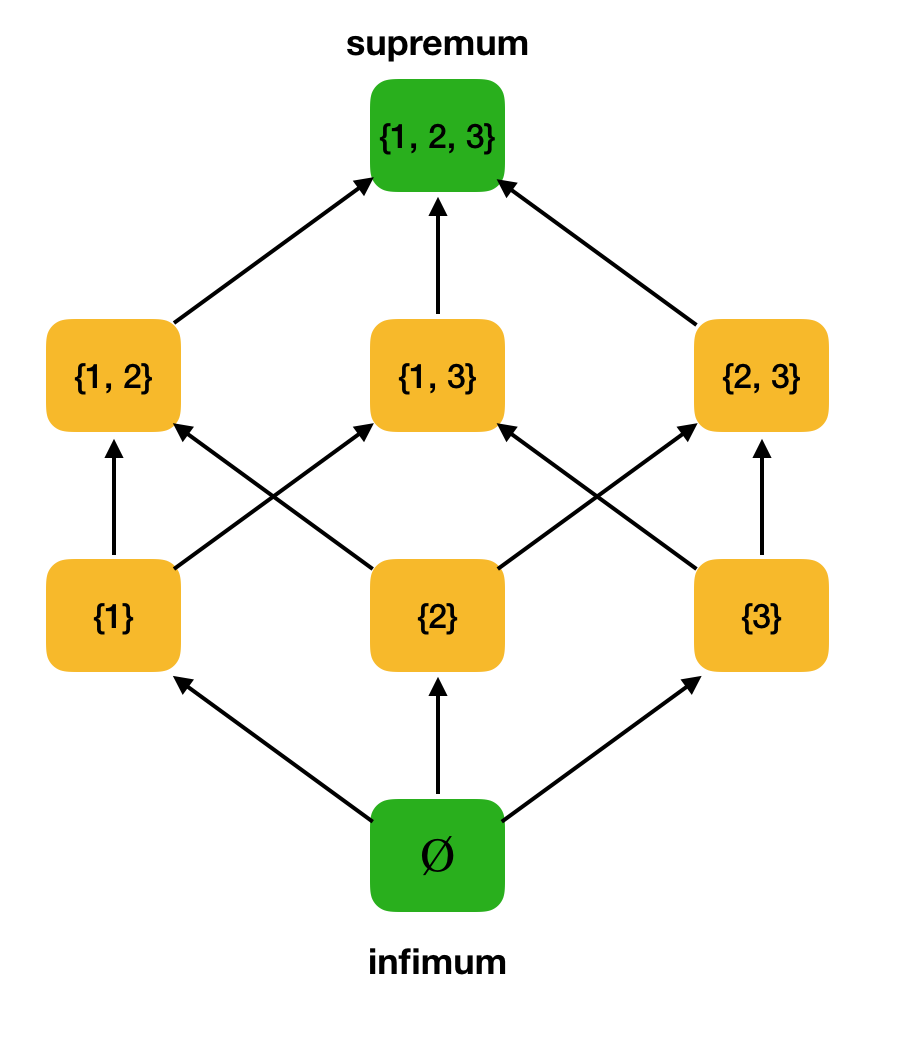
定义3.令⟨S，⩽⟩是部分有序集，⊆⊆S。A的上边界是元素u∈S，因此∀x∈A：x⩽u。 令U为A的所有上限的集合。如果U具有最小的元素，则称其为supremum并由sup A表示。

类似地，引入了精确下限的概念。

定义4.令⟨S，⩽⟩为部分有序集A⊆S。A的下边界是元素l∈S，使得∀x∈A：l⩽x。 令L为A的所有下界的集合。如果L具有最大的元素，则称其为无穷大，并由inf A表示。

作为示例，考虑上述部分有序集⟨P（{1，2，3}），，并在其中找到最高和最低值：



现在我们可以公式化代数格的定义。

定义5.令⟨P，⩽⟩为部分有序集，以使每个两个元素的子集都有确切的上下限。 P称为代数格。 此外，sup {x，y}写为x y，而inf {x，y}-写为x y。

我们验证我们的工作示例⟨P（{1，2，3}），⊆⟩是一个网格。 实际上，对于任何a，b∈P（{1，2，3}），a∨b=a∪b和a∧b=a∩b。 例如，考虑集合{1，2​​}和{1，3}并找到它们的最小和最大。 如果我们越过它们，我们将得到集合{1}，这将是无足轻重的。 我们通过他们的联合获得最高权力-{1,2,3}。

在FD检测算法中，搜索空间通常以格子的形式表示，其中一个元素的集合（读取搜索格子的第一层，其中依赖项的左侧部分由一个属性组成）是原始关系的每个属性。
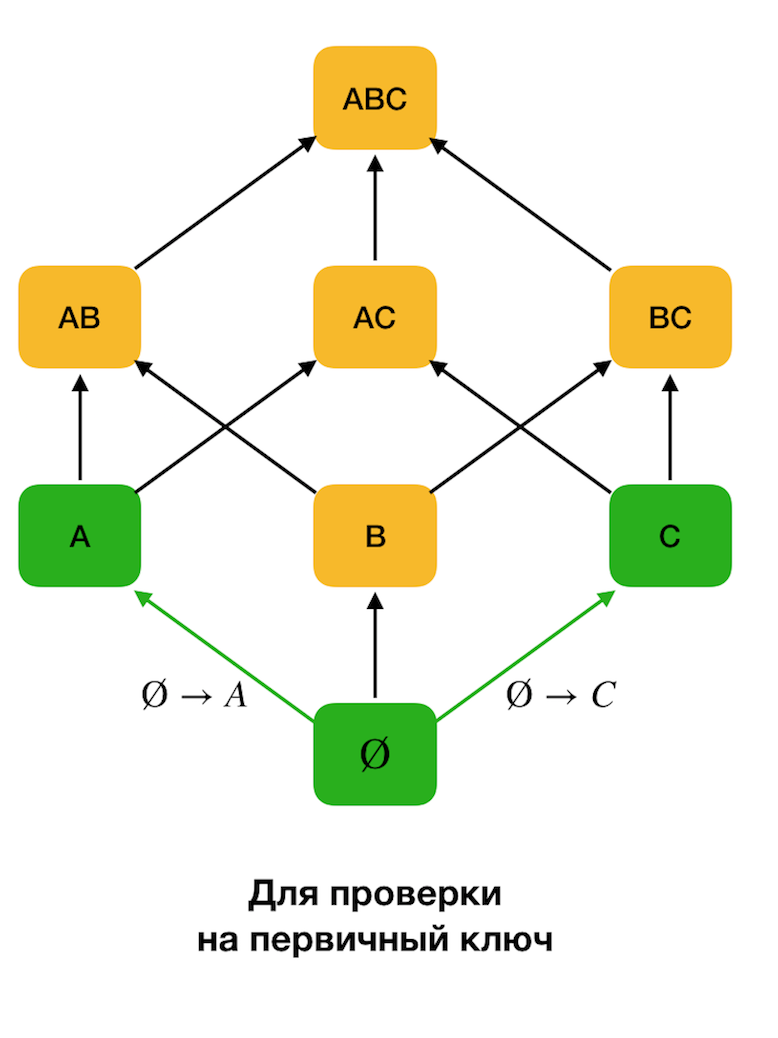
首先， 考虑形式∅→ 单个属性的依赖性。 此步骤使您可以确定哪些属性是主键（此类属性没有行列式，因此左侧为空）。 此外，这种算法使晶格向上移动。 值得注意的是，不能完全绕开晶格，也就是说，如果将所需的左侧部分的最大尺寸传输到输入，则算法将不会超出该尺寸的级别。

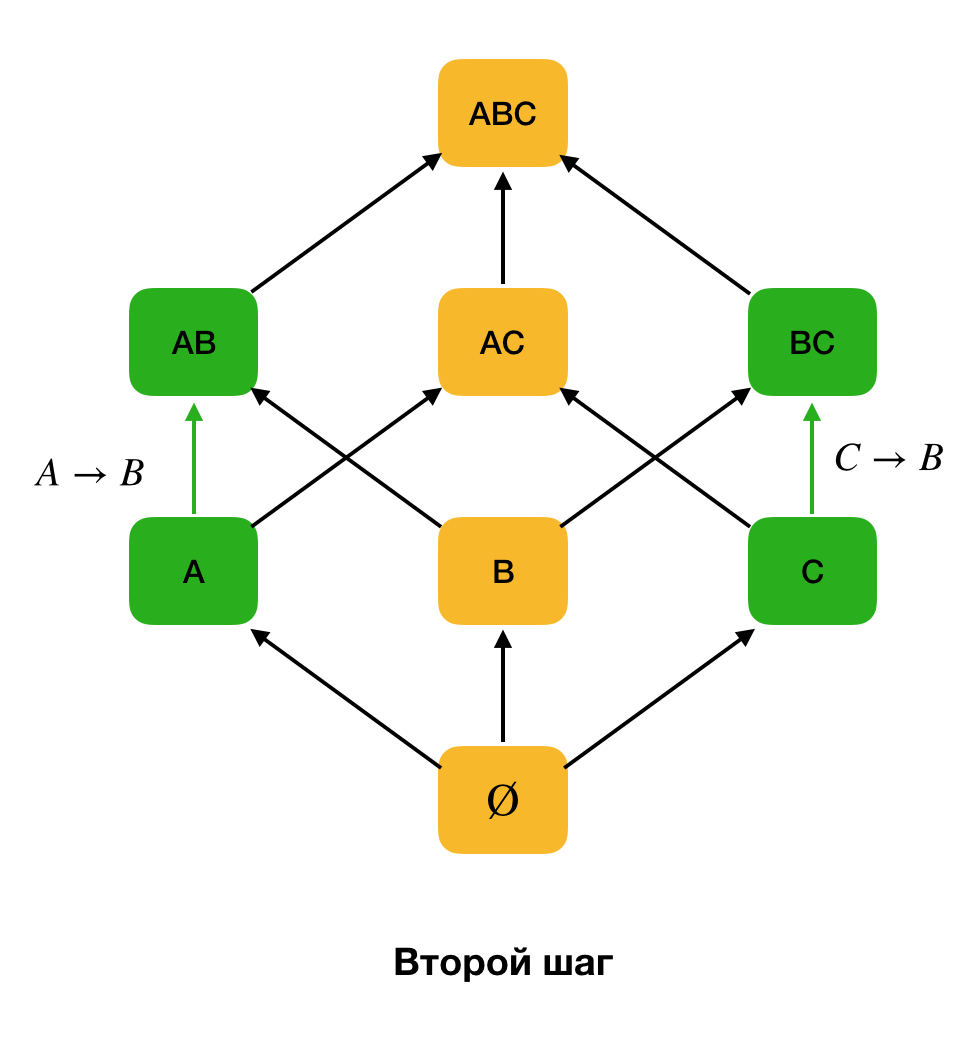
下图显示了如何在联邦法律的搜索问题中使用代数格。 在此，每个边缘（ X，XY ）表示依存关系X→Y。 例如，我们经历了第一级，我们知道保持了依存关系A→B （我们将通过顶点A和B之间的绿色连接来显示此依存关系）。 因此，当我们向上移动晶格时，我们将无法检查依赖性A，C→B ，因为它将不再是最小的。 同样，如果保持依赖关系C→B ，我们将不会对其进行测试。




另外，通常，所有现代FZ搜索算法都使用这样的数据结构作为分区（原始源中的分割分区[1]）。 分区的正式定义如下：

定义6.令X⊆R是关系r的属性集。 集群是r中具有相同X值的元组索引集合，即c（t）= {i | ti [X] = t [X]}。 分区是一组群集，不包括单位长度的群集：

$$

$$\ pi（X）：= \ {c（t）| | t \ in r \楔| c（t）| > 1 \}$$

简而言之，属性X的分区是一组列表，其中每个列表都包含具有与X相同值的行号。 在现代文献中，表示分区的结构称为位置列表索引（PLI）。 PLI压缩不包括单位长度簇，因为它们是仅包含具有唯一值的记录号的簇，该值总是易于设置的。

考虑一个例子。 让我们回到与患者相同的表，并为“ 患者”和“ 保罗”列构建分区（左侧出现一个新列，其中标记了该表的行号）：





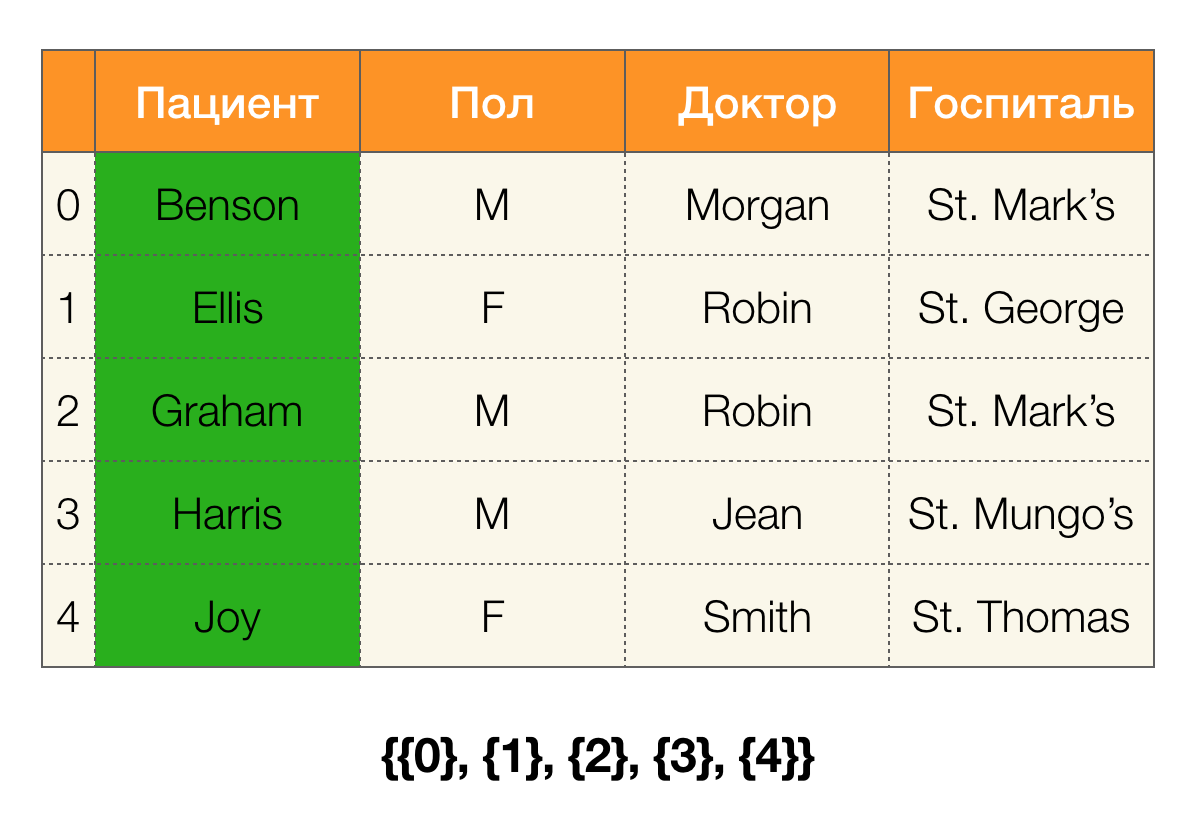
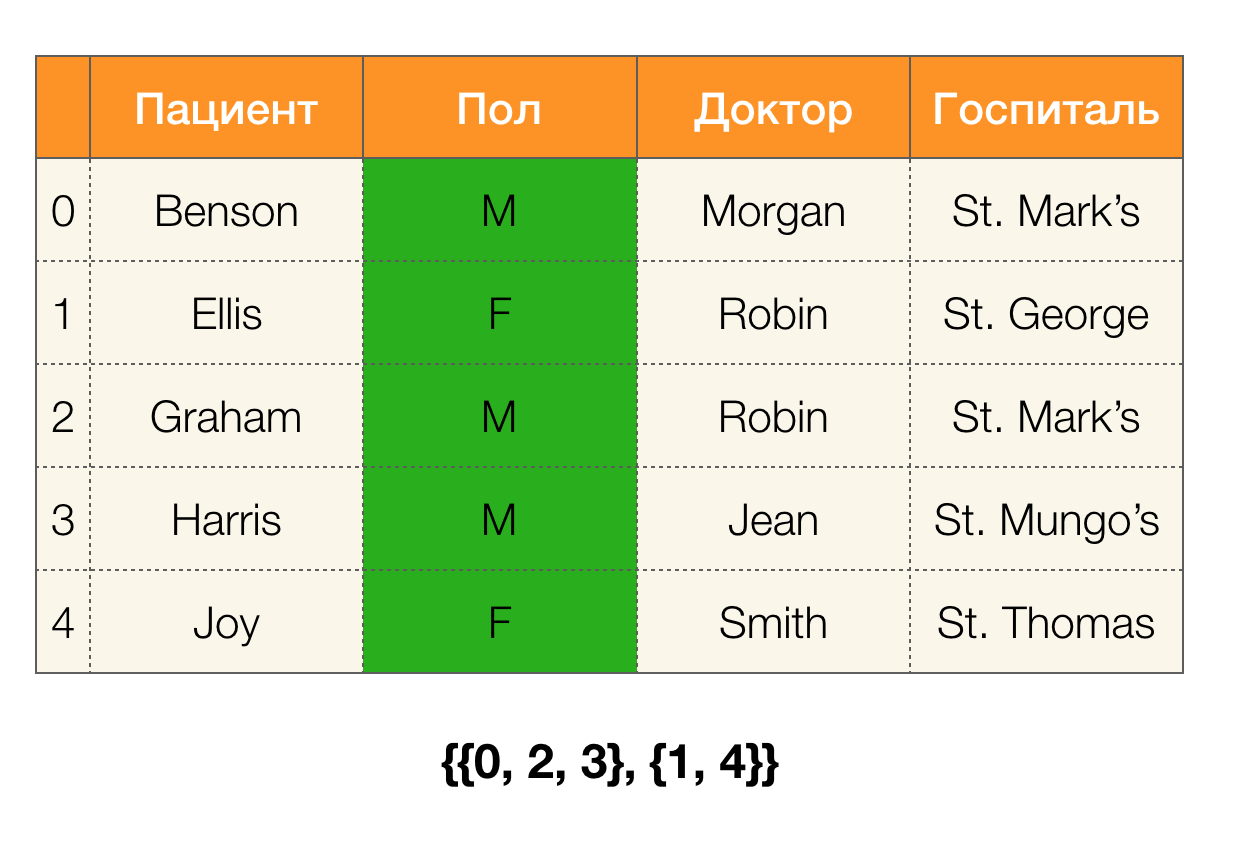
此外，根据定义，“ 患者”列的分区实际上将为空，因为单个群集已从该分区中排除。

可以通过几个属性获得分区。 为此，有两种方法：遍历表，根据所有必要属性立即构建分区，或使用沿属性子集交叉分区的操作来构建分区。 FZ搜索算法使用第二个选项。

简单来说，例如， 要按ABC列进行分区，可以对AC和B （或任何其他不交集的子集）进行分区，并使它们彼此相交。 两个分区的交集操作确定了两个分区共有的最大长度的群集。

让我们看一个例子：





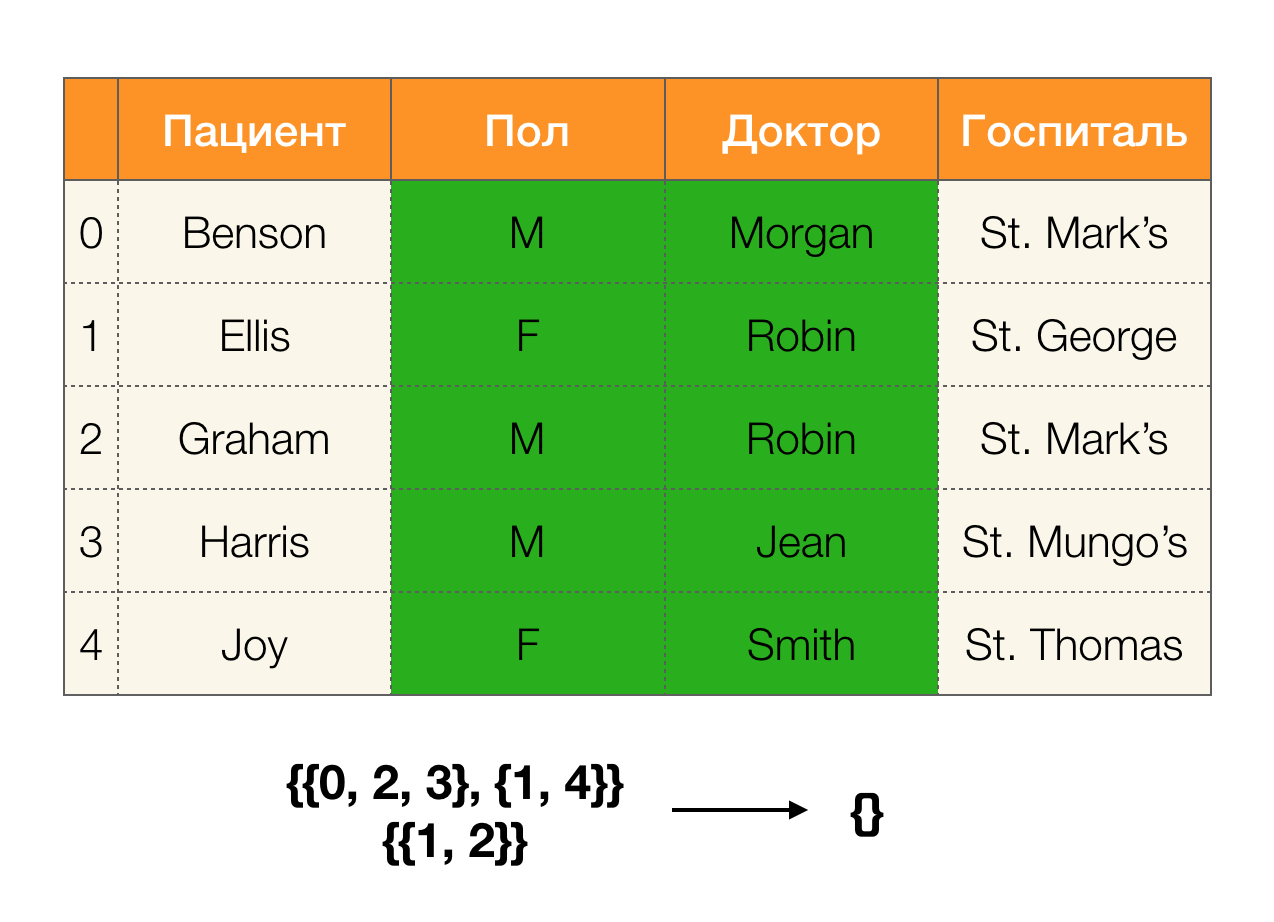
在第一种情况下，我们收到了一个空分区。 如果仔细查看该表，则实际上两个属性的值并不相同。 如果我们稍微修改表格（右边的情况），那么我们已经得到了一个非空的交集。 同时，第1行和第2行实际上包含属性Paul和Doctor的相同值。

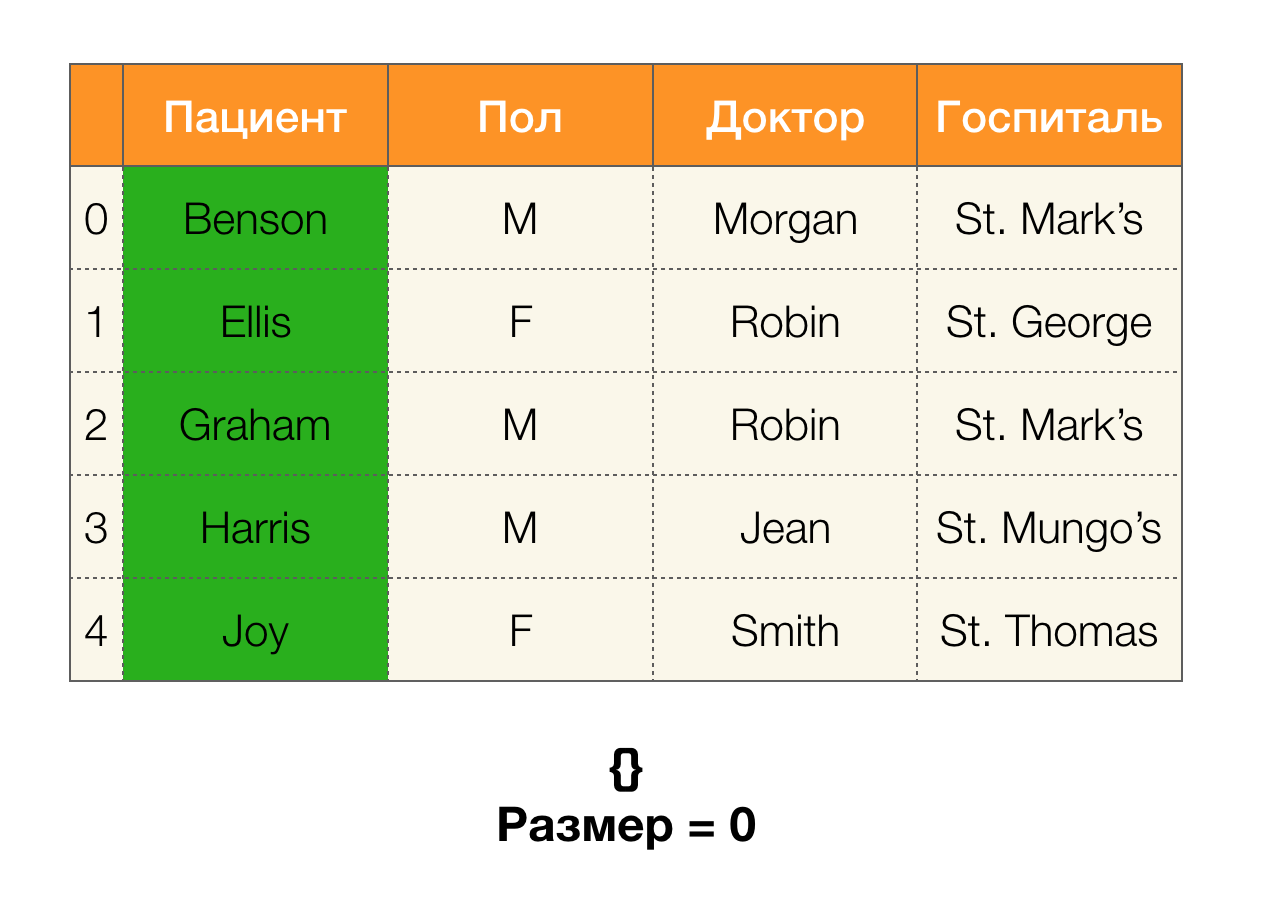
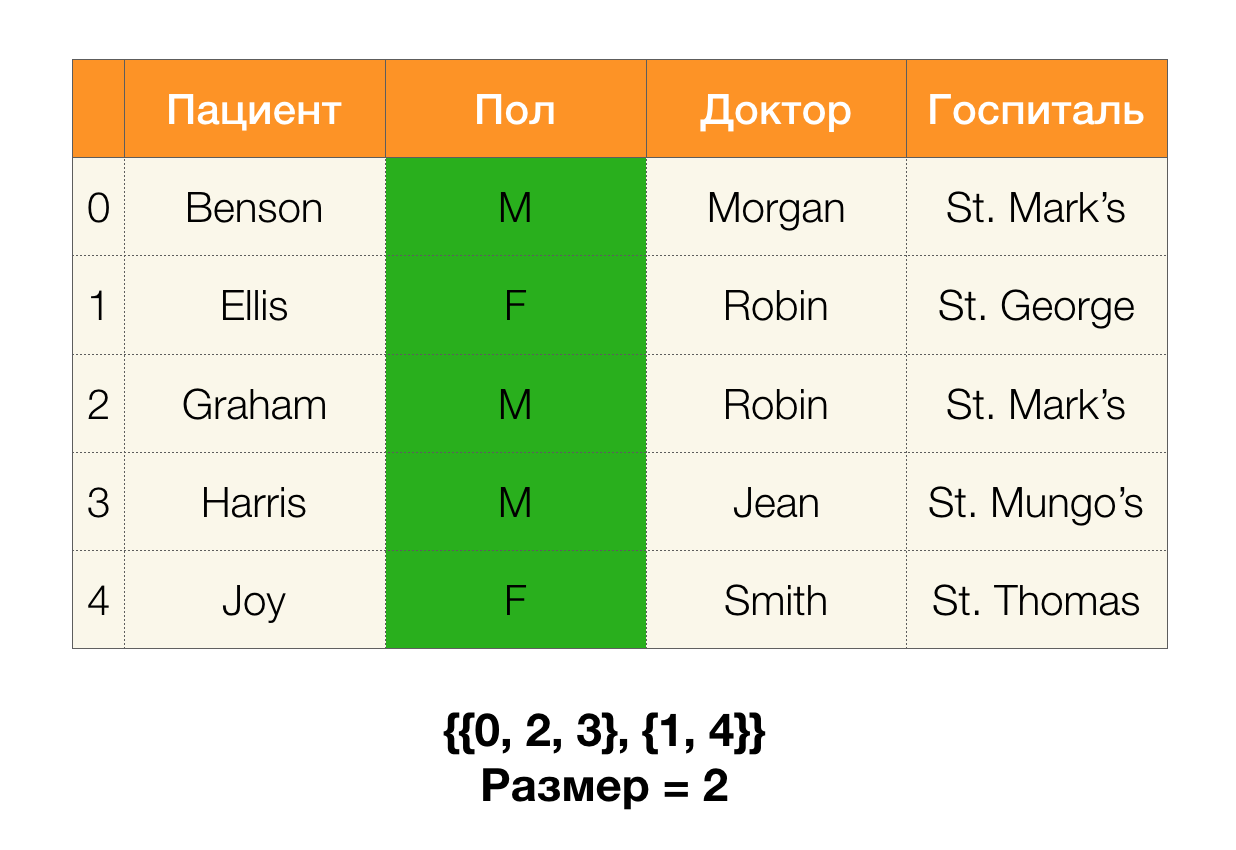
接下来，我们需要诸如分区大小的概念。 正式地：

$$

$$| \ pi（X）| = | \ {c \ in \ pi（X）：| c | > 1 \} |$$

简而言之，分区大小是分区中包含的群集数（请记住，分区中不包含单个群集！）：





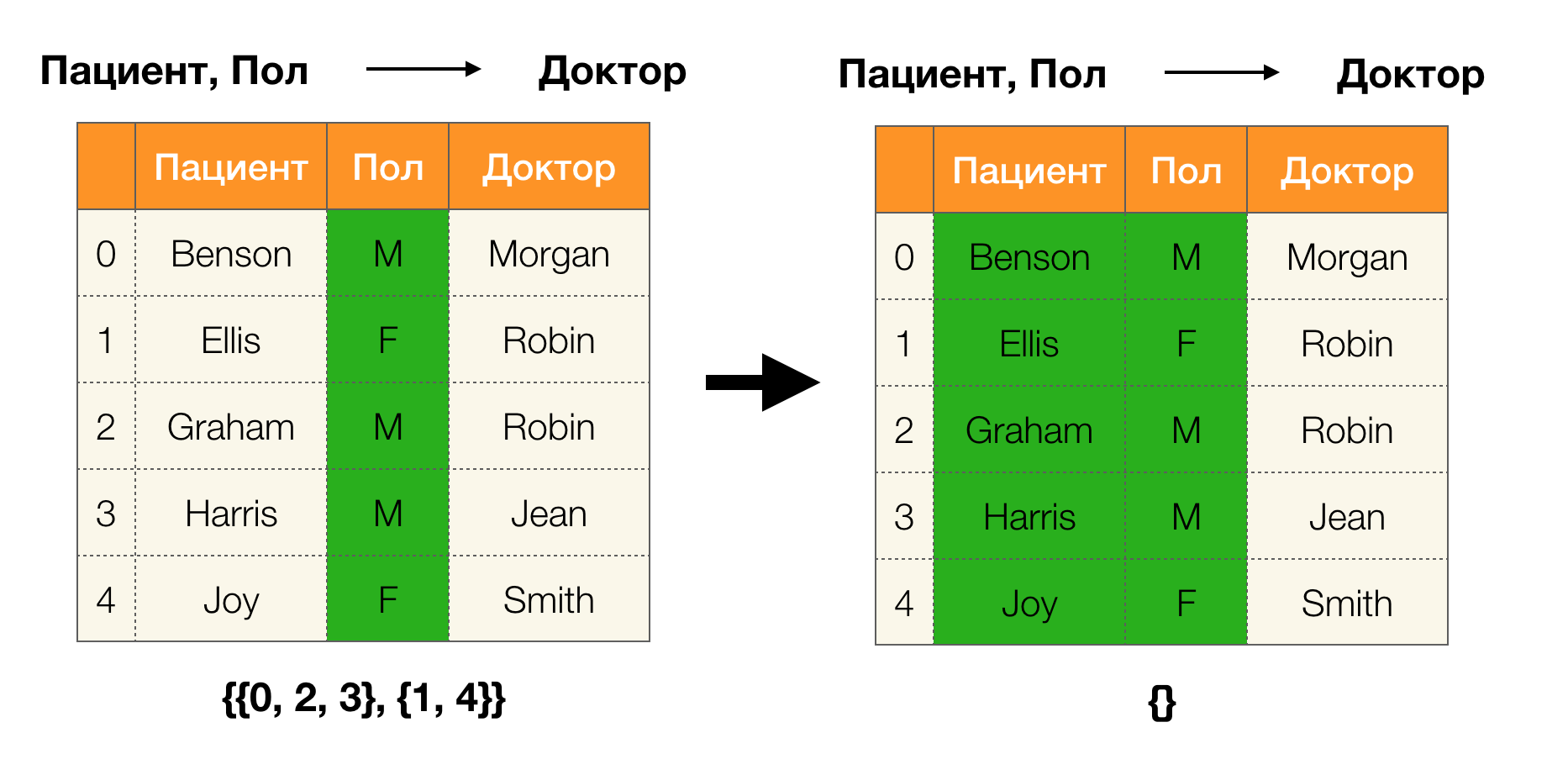
现在，我们可以定义一个关键引理，对于给定的分区，它可以让我们确定是否保持依赖关系：

引理1 。 仅当且仅当满足依存关系A，B→C

$$

$$| \ pi（AB）| = | \ pi（AB \ cup \ {C \}）|$$

根据引理，为了确定是否保留依赖项，必须执行四个步骤：

1. 计算依赖项左侧的分区
2. 计算依赖关系右侧的分区
3. 计算第一步和第二步的乘积
   
4. 比较第一步和第三步获得的分区大小
   

以下是检查此引理是否保持依赖性的示例：






在本文中，我们研究了功能依赖，近似功能依赖等概念，研究了它们的使用位置以及存在哪些联邦法律搜索算法。 我们还详细研究了在现代算法中积极使用的基本但重要的概念，以寻求联邦法律。

参考文献：

1. Huhtala Y.等。 TANE：一种发现功能和近似依赖关系的有效算法//计算机日记。 -1999.-T. 42.-No. 2.-S.100-111。
2. Kruse S.，Naumann F.近似依存关系的有效发现// VLDB Endowment的会议记录。 -2018.-T.11。-No. 7.-S.759-772。
3. Papenbrock T.，Naumann F.一种功能依赖发现的混合方法// // 2016年国际数据管理大会会议录。 -ACM，2016年。-S. 821-833。
4. Papenbrock T.等。 功能依赖发现：七个算法的实验评估// VLDB Endowment的论文集。 -2015.-T. 8.-否。 10.-S.1082-1​​093。
5. Kumar A.等。 要加入还是不加入？：在功能选择之前三思而行/// 2016年国际数据管理大会会议录。 -ACM，2016年。-S. 19-34。
6. Abo Khamis M.等。 张量稀疏的数据库内学习//第37届ACM SIGMOD-SIGACT-SIGAI数据库系统原理研讨会论文集。 -ACM，2018年。-S.325-340。
7. 海勒斯坦JM等。 MADlib分析库：或MAD技能，即VLDB Endowment的SQL //录。 -2012.-T. 5.-否。 12.-S.1700-1711。
8. Qin C.，Rusu F.万亿级分布式梯度下降优化的推测近似//第四次云中数据分析研讨会的论文集。 -ACM，2015年。-S. 1。
9. Meng X.等。 Mllib：Apache Spark中的机器学习//机器学习研究杂志。 -2016.-T. 17.-不。 1 .-- S.1235-1241。

: , JetBrains Research , CS , JetBrains Research