序言
最近,需要从头创建一个实现单纯形方法算法的程序。 但是在解决方案的过程中,我遇到了一个问题:互联网上没有那么多资源,您可以查看该算法的详细理论分析(其原理:为什么要采取这些步骤或那些步骤)以及实用的实现技巧-直接是该算法。 然后,我向自己许下了诺言-完成任务后,我将就该主题写我的帖子。 实际上,我们将讨论这一点。
备注。 该帖子将以相当正式的语言撰写,但会提供评论,这应该使内容更加清晰。 这种格式将保留科学方法,同时也可能有助于研究该问题。
§1。 线性规划问题的陈述
定义:线性规划是一门数学学科,致力于解决由线性方程和不等式系统定义的n维空间集上的极值问题的理论和方法。
线性规划的一般任务(以下简称LP)的形式为:
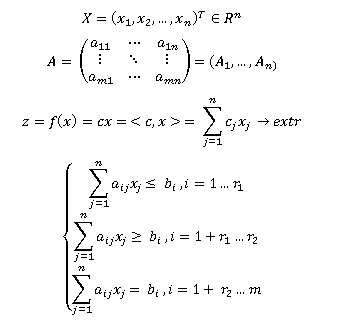
§2。 LP问题的规范形式
LP问题的规范形式:
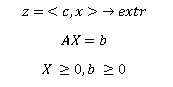 注意:
注意:任何LP问题都归结为规范。
从任意LP问题转换为规范形式的算法:
- 负数不等式 $内联$ b_i $内联$ 乘以(-1)。
- 如果不等式形式为(≤),则将其添加到左侧 $内联$ s_i $内联$ 是一个附加变量,我们获得相等性。
- 如果形式不等式(≥),则从左侧减去 $内联$ s_i $内联$ ,我们得到平等。
- 我们进行变量的替换:
- 如果 $内联$ x_i≤0 $内联$ 然后 $内联$ x_i'= -x_i≥0 $内联$
- 如果 $内联$ x_i $内联$ -任何 $ inline $ x_i = x_i'-x_i''$ inline $ 在哪里 $内联$ x_i',x_i''≥0 $内联$
注意:我们会编号
$内联$ s_i $内联$ 根据我们添加的不平等数。
注意事项: $内联$ s_i $内联$ ≥0。
§3。 角点。 基本/免费变量。 基本解决方案
定义:点
$内联$ X∈D $内联$ 如果表示形式称为角点
$ inline $ X =αX^ 1 +(1-α)X ^ 2,其中X ^ 1,X ^ 2∈D; 0 <α<1 $ inline $ 只能与
$ inline $ X ^ 1 = X ^ 2 $ inline $ 。
换句话说,不可能在该区域中找到两个点,通过该点的间隔包含
$内联$ X $内联$ (即
$内联$ X $内联$ 不是内部观点)。
解决LP问题的图形方法表明,找到最佳解与角点有关。 这是开发单纯形方法时的基本概念。
定义:假设有一个包含m个方程和n个未知数的系统(m <n)。 我们将变量分为两组:(nm)我们将变量设置为零,剩下的m个变量是通过求解初始方程组确定的。 如果此解决方案是唯一的,则非零的m变量称为基本变量; 零(nm)变量-自由(非基本)变量的相应结果值称为基本解决方案。
§4。 单纯形法
单纯形法可让您有效地找到最佳解决方案,而无需简单列举所有可能的拐角点。 该方法的主要原理:计算从某种“开始”基本解开始,然后搜索“改善”目标函数值的解。 这仅在某些变量的增加导致功能值增加的情况下才是可能的。
应用单纯形方法的先决条件:
- 任务必须具有规范形式。
- 该任务应有明确的基础。
定义:明确选择的基础是以下形式的向量:
$ inline $(..0100 ..)^ T,(..010 ..)^ T,(.. 0010 ..)^ T ... $ inline $ ,即 向量中只有一个坐标为非零且等于1。
注意:基本向量的维数为(m * 1),其中m是约束系统中的方程数。
为了方便计算和可视化,通常使用单纯形表:
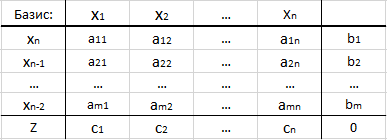
- 第一行表示所有变量的“名称”。
- 在第一列中,指示基本变量的数字,在最后一个单元格中,指示字母Z(这是功能行)。
- 在“表格中间”中,指出约束矩阵的系数-aij。
- 最后一列是约束系统相应方程式右侧的向量。
- 最右边的单元格是目标函数的值。 在第一次迭代时,假定为0。
注意:基础是变量,即约束矩阵中的系数,在这些矩阵处形成基矢量。
注意:如果原始问题中的约束条件由形式≤的不等式表示,则当问题简化为规范形式时,引入的其他变量将构成初始基本解。
注意:功能行中的系数以“-”号表示。
单纯形法算法:1.选择一个将在基础中引入的变量。 这是根据前面指出的原理完成的:我们必须选择一个变量,该变量的增加将导致功能的增加。 根据以下规则进行选择:
- 如果任务最少,请在最后一行中选择最大的正数元素。
- 如果任务最多,请选择最小负数。
实际上,这种选择与上述原理相对应:如果任务最少,那么我们减去的数字越大,功能的降低就越快; 相反,最大数量-添加的数量越大,功能增长越快。
注意:尽管我们将问题中的最小负数设为最大,但该系数表示函数的增长方向,因为 单纯形表中的功能行以“-”号表示。 最小化时的类似情况。
定义:单纯形表中与所选系数相对应的
列称为
前导列 。
2.选择一个我们将在基础中引入的变量。 为此,您需要确定在新的基本变量增长时最有可能消失的基本变量。 从代数上讲,此操作如下:
- 右手部分的向量除以终止列
- 在获得的值中,选择最小的正值(不考虑负值和零答案)
定义:这种线称为
引导线 ,对应于要从基准派生的变量。
注意:实际上,我们从约束系统的每个方程式到其余变量表示旧的基础变量,并查看在哪个方程式中新基础变量的增加极有可能为0。进入这种情况意味着我们“绊倒”了一个新的顶点。 这就是为什么不考虑零和负元素的原因,因为 获得这样的结果意味着选择这样一个新的基本变量将使我们远离没有解决方案的领域。
3.我们正在寻找一个位于行首与列相交处的元素。
定义:这样的元素称为
前导元素 。
4.在第一列(带有基本变量的名称)中,而不是要排除的变量中,写下我们输入到基础中的变量的名称。
5.接下来,开始计算新的基本解的过程。 它使用
Jordan-Gauss方法发生 。
- 新引线=旧引线/引线
- 新行=新行-首列中的行因子*新首行
注意:这种转换的目的是将所选变量引入基础,即 前导列作为基本向量的表示形式。
6.之后,我们检查最优条件。 如果生成的解决方案不是最佳解决方案,请再次重复整个过程。
§5。 单纯形法结果的解释
1.最优性所得解决方案的最优条件:
- 如果任务最多,则功能行中不存在负系数(即,如果变量有任何变化,则所得功能的值将不会增长)。
- 如果任务最少,则功能行中没有正系数(即,如果变量有任何变化,则所得功能的值不会减少)。
2.无限功能但是,值得注意的是,给定功能可能无法在给定区域内达到最大值/最小值。 它的代数属性可以表示为:
选择前导行(可变变量除外)时,右侧矢量除以前导列的按词除法的结果仅包含零和负值。
实际上,这意味着无论我们设置新的基本变量有多大的增长,我们都将永远找不到新的顶点。 因此,我们的功能不仅限于可行的解决方案。
3.替代解决方案当找到最佳解决方案时,另一种选择是可能的-存在替代解决方案(另一个拐角给出相同的功能值)。
存在替代的代数符号:
达到最佳解后,功能行中的自由变量系数为零。
这意味着随着系数为零的相应变量的增长,该函数的值将不会改变,并且新的基本解也将给出该函数的最佳值。
结语
本文旨在对理论部分有更深入的了解。 在这里的评论和解释中,您可以获得对问题的答案,这些问题通常是在研究此方法时先验省略的。 但是,必须理解,数值优化的许多方法都是基于单纯形法(例如
Gomori方法 ,
M方法 ),如果没有基本了解,那么在进一步研究和应用此类的所有算法中不太可能取得很大进展。
稍后,我将写一篇有关单纯形方法实际实现的文章,以及几篇有关人工变量方法(M方法),Gomori方法以及分支和边界方法的文章。
感谢您的关注!
聚苯乙烯如果您已经对单纯形方法的实施感到烦恼,我建议您阅读A. Taha所著
的《运筹学概论》 ,无论是在理论上还是在实例上,都对它进行了详尽的分析。 并查看解决matburo.ru问题的示例-这将有助于代码实现。