 我博客中的原始翻译
我博客中的原始翻译这本书是怎么给我的?
2017年5月,我收到了我的中学老师乔治·鲁特(George Rutter)的一封电子邮件,他在信中写道:“
我有一本德国的狄拉克大书(Die Prinzipien der Quantenmechanik)的副本,该书属于艾伦·图灵,其后当我读你的书“ 创意者”时 ,在我看来,你是需要它的人 。“ 他向我解释说,他从另一本(当时已故)我的学校老师
诺曼·鲁特里奇 (
Norman Rutledge )那里收到了一本书,我知道他是艾伦·图灵(Alan Turing)的朋友。 乔治在信中写道:“
如果您需要这本书,下次您来英格兰时,我可以把它交给您 。”
在2019年3月过了几年之后,我真的到达了英格兰,之后我同意乔治在牛津的一家小旅馆里吃早餐。 我们吃了饭,聊天,等着食物定下来。 然后是时候讨论这本书了。 乔治把手放在公文包中,拿出设计合理的典型1900年代中期学术量。

我打开封面,想知道它是否可以在铭文的背面:“
Alan Turing的
财产”之类。 但是,不幸的是,事实并非如此。 尽管如此,它仍然附有一张充分表达力的注释,该注释写于2002年,从Norman Rutledge到George Rutter,共四页。
1970年代初,我还是
伊顿 高中生时就认识诺曼·鲁特里奇(Norman Rutledge)。 他是一位数学老师,绰号The Nutty Norman。 他在各个方面都是一位令人愉快的老师,并讲述了无数关于数学和其他有趣事物的故事。 他负责确保学校收到一台计算机(用打孔的胶带编程,宽达书桌的宽度),这是
我使用过的第一台计算机 。
在那些日子里,我对诺曼的过去一无所知(请记住,那是在互联网出现之前很久了)。 我只知道他是“鲁特利奇博士”。 他经常讲关于剑桥人的故事,但在他的故事中他从未提到艾伦·图灵。 当然,图灵当时还不够出名(尽管事实证明,我已经在
Bletchley Park (第二次世界大战期间加密中心所在的豪宅)认识一位认识他的人听说过他)。
艾伦·图灵(Alan Turing)直到1981年
才开始出名,那时我
才开始研究简单的程序 ,尽管那时是在细胞自动机的背景下,而不是
图灵机 。
突然有一天,我在
加利福尼亚理工学院的图书馆里浏览卡片目录,偶然发现了他的母亲莎拉·图灵(Sarah Turing)写的《
艾伦 ·图灵》。 这本书有很多信息,包括图灵未出版的生物学科学著作。 但是,由于这本书没有提及任何关于他与诺曼·鲁特里奇(Norman Rutledge)的关系,所以我没有学到任何东西(尽管据我发现,莎拉·图灵(Sarah Turing)
就这本书与诺曼进行了往来往来,甚至诺曼甚至
对它进行了
评论 )。

十年后,由于对Turing及其他(当时未发表的)
生物学工作非常好奇,我参观了位于
剑桥国王学院的
Turing档案 。 很快,我熟悉了他们从图灵的作品中获得的收益,并花了一些时间在上面,所以我想同时我也可以请他查看他的私人信件。 翻阅它,我发现
了艾伦·图灵给诺曼·鲁特里奇(Norman Rutledge)的
几封信 。
到那时,安德鲁·霍奇斯
( Andrew Hodges)的
传记出版了,以至于图灵终于成名,这证实了艾伦·图灵和诺曼·鲁特里奇是真正的朋友,而且图灵是诺曼的科学顾问。 我想问鲁特里奇有关图灵的事,但那时诺曼已经退休,过着僻静的生活。 但是,当我在2002年(十年退修后)完成《
新类型的科学 》一书的工作时,我对其进行了追踪并寄给他一本书的标题为“致我的最后一位数学老师”。 然后我们
联系了一下,2005年,我再次来到英格兰,同意与诺曼见面,在伦敦市中心的一家豪华酒店喝杯茶。
我们对很多事情进行了精彩的演讲,包括艾伦·图灵。 诺曼(Norman)的故事始于50年前,当时他对图灵(Turing)确实很了解,从而开始了我们的对话。 但是尽管如此,他个人
还是有话要说 :“
他不善交际 。” “
他咯咯笑了 。” “
他不能真正与非数学家交谈 。” “
他总是害怕让母亲难过 。” “
他白天离开并参加了马拉松比赛 。” “
他不太有野心 。” 然后谈话恢复了诺曼的身份。 他说,尽管事实上他已经退休了16年,但他仍然为“
数学报纸 ”撰写文章,以他的话说,“
在去另一个世界之前完成所有的科学工作 ”在他的脸上露出几乎无法察觉的笑容时,“
所有数学真理肯定都会被揭露 。” 茶话会结束后,诺曼(Norman)穿上皮夹克前往轻便摩托车,完全忽略了当天
爆炸所造成的伦敦交通中断 。
这是我最后一次见到诺曼,他于2013年去世。
六年后,我和George Rutter一起吃早餐。 与我一起是Rutledge在2002年以他独特的笔迹写的便条:

起初,我流利地读了笔记。 她像往常一样富有表现力:
我从他的朋友兼执行者罗宾·甘迪 ( Robin Gandy)那里收到了一本阿兰·图灵(Alan Turing)的书(在国王学院,从死者同志的藏书中分发书籍是正常的,我从艾佛·拉姆西 ( Ivor Ramsey )的书中选择A.E. Houseman的诗集作为合适的礼物(他是院长和[在1956年]从教堂跳下)...
后来他在简短的笔记中写道:
您会问,这本书到底应该去哪儿?我认为,这本书应该寄给那些欣赏与图灵作品有关的一切的人,所以它的命运取决于您。
斯蒂芬·沃尔夫拉姆(Stephen Wolfram)给我寄来了他印象深刻的书,但我没有深入研究……
最后,他祝贺乔治·鲁特(George Rutter)勇于退休后勇往直前搬到澳大利亚(表示结果是暂时的),并说他本人将“
搬迁到斯里兰卡,作为廉价和类似莲花的存在的例子, ”但补充说:“
那里发生的
事件表明他不应该这样做 ”(显然是指斯里兰卡的
内战 )。
那么这本书的肠子里隐藏着什么?
因此,我如何处理一本保罗·狄拉克(Paul Dirac)曾经属于艾伦·图灵(Alan Turing)的德语书籍的副本。 我没有读德语,但我
有 1970年代版
的同一本书的英文
副本 (这是其原文)。 不过,在早餐后,我认为应该逐页仔细阅读本书,这是对的。 最后,这是处理古董书籍时的常见做法。
应该指出的是,狄拉克(Dirac)演讲的优雅让我震惊。 该书于1931年出版,但其纯粹的形式主义(是的,尽管存在语言障碍,我仍然可以阅读书中描述的数学)与今天所写的几乎相同。 (我不想在这里过多地关注Dirac,但我的朋友
Richard Feynman告诉我,至少在他看来,Dirac的演讲是单音节的。NormanRutledge告诉我,他是
Dirac的养子在剑桥的朋友,他
的儿子是Dirac的理论家。诺曼经常在狄拉克家中,他说“伟人”有时会逐渐淡出背景,而前景总是有很多数学难题。不幸的是,我本人从未见过保罗·狄拉克,尽管有人告诉我 哇,他终于离开剑桥,去了佛罗里达,他失去了以前的大部分精力,成为了一个很友善的人。
但是回到狄拉克的书,那是图灵的书。 在第9页上,我注意到用简单铅笔书写的下划线和小边距注释。 我继续翻页。 经过几章,笔记消失了。 但是,突然之间,我在第127页中发现了一个注释,内容如下:
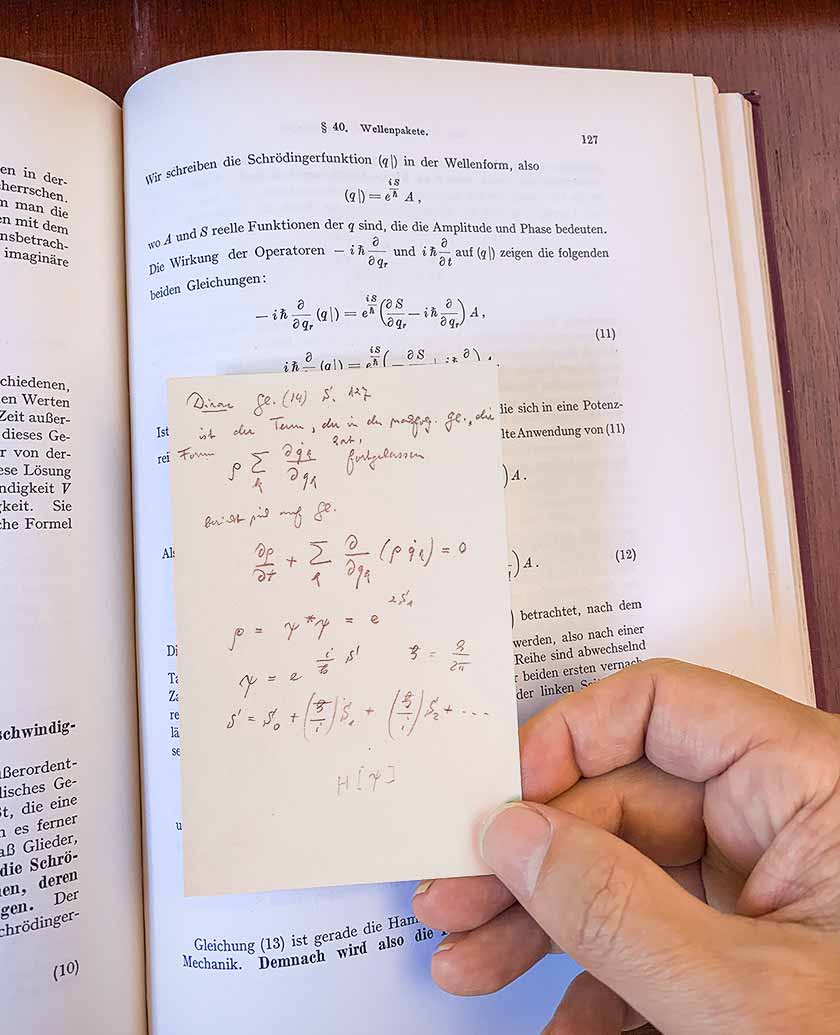
它是用标准的德语手写体以德语编写的。 看来它可以以某种方式与
拉格朗日力学联系起来 。 我认为可能是在图灵之前有人拥有这本书的,这一定是这个人写的笔记。
我继续翻阅这本书。 没有笔记。 我以为我找不到任何东西。 但是,在第231页上,我发现了公司书签-带有印刷文本:

我最终会找到其他东西吗? 我继续翻阅这本书。 然后,在书的最后,第259页,关于电子的相对论的这一部分,我发现了以下内容:

我展开了这张纸:
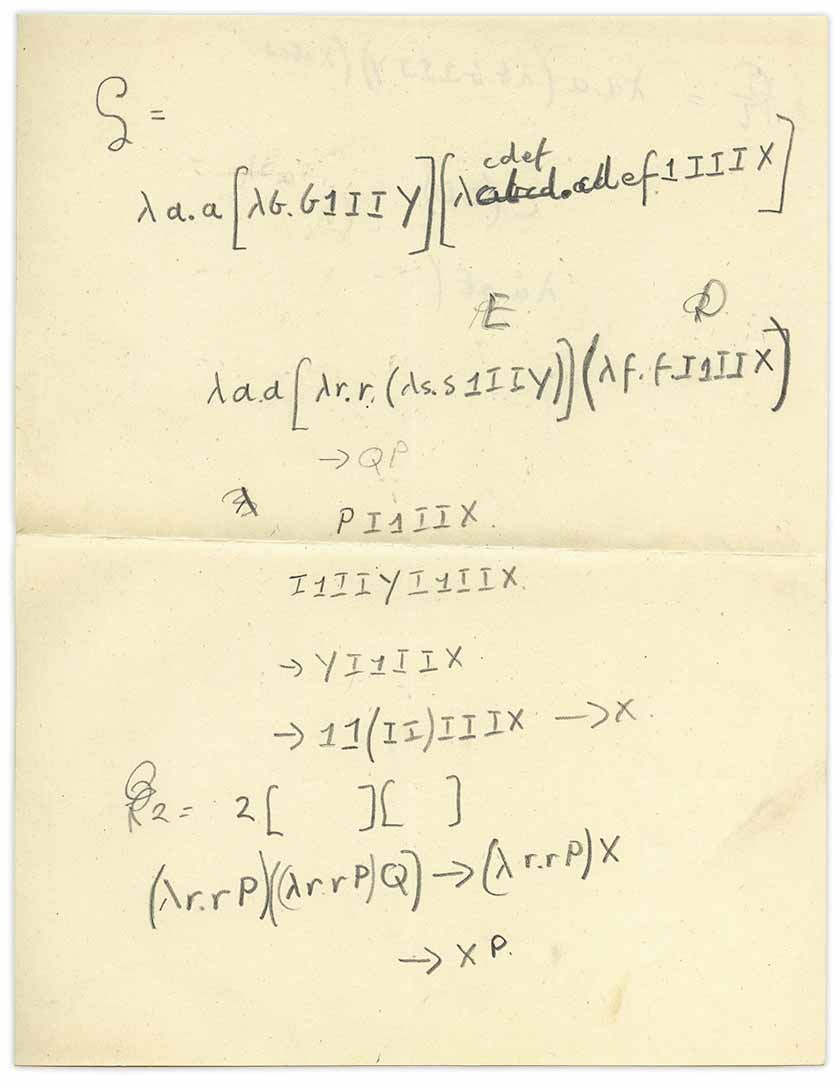
我立刻意识到这是一个混合了
混合器的lambda演算 ,但是这张表是怎么出现的呢? 回想一下,这本书是一本有关量子力学的书,但是所附的表格处理的是数学逻辑,即现在所说的计算理论。 这是图灵作品的典型代表。 我想知道图灵是否亲自写过这张纸条。
即使在早餐时,我也在互联网上搜索图灵的笔迹样本,但没有找到计算形式的例子,因此我无法得出有关笔迹确切身份的结论。 很快我不得不走了。 我仔细包装了这本书,准备揭开该页的内容和作者的秘密,然后随身携带。
关于这本书
首先,让我们讨论这本书本身。 保罗·狄拉克(Paul Dirac)撰写的
《量子力学原理》于1930年以英文出版,并很快被翻译成德文。 (狄拉克的序言日期为1930年5月29日;该译者的译名是
维尔纳·布洛赫 (
Werner Bloch) ,于1930年8月15日。)这本书成为量子力学发展的里程碑,系统地建立了清晰的形式主义以进行计算,并在其他方面解释了狄拉克对
正电子的预测,这将成为于1932年开业。
为什么艾伦·图灵(Alan Turing)有一本书是德语的,而不是英语的? 我不确定这一点,但是在那些日子里,德语是科学的主要语言,我们知道艾伦·图灵能够阅读。 (毕竟,在他著名的
图灵 机作品的标题中,“
关于可计算数字及其解决方案的附录 (Entscheidungsproblem),它是一个很长的德语单词-在本文的主要部分中,他使用“德语字母”形式的晦涩哥特式字符,他使用了该字符,而不是例如希腊字符。
艾伦·图灵(Alan Turing)自己买了书还是递给他? 我不知道 在图灵的书的封面内侧,有一个铅笔符号“ 20 /-”,这是标准符号“ 20先令”,类似于1英镑。 右页上有一个被删去的“ 26.9.30”,据说是1930年9月26日-也许是这本书首次购买的日期。 然后,在最右角,删除的数字为“ 20”。 也许这又是价格。 (如果假设这本书是在德国出售的,这可能是德国马克的价格吗?当时,1马克的价值约等于1先令,德国的价格可能会写成“ 20 RM”。)最后,在封底的内部是“ c 5 /-”-也许是(以很大的折扣)二手书的价格。
让我们看一下艾伦·图灵(Alan Turing)生平的主要日期。 艾伦·图灵
( Alan Turing
)生于1912年6月23日 (巧合的是,正好比
Mathematica 1.0早76年)。 在1931年秋天,他进入了剑桥国王学院。 在1934年经过标准的三年学习后,他获得了学士学位。
在1920年代和1930年代初期,量子力学是一个热门话题,艾伦·图灵当然对此很感兴趣。 从他的档案中我们知道,在1932年,这本书出版后,他就获得了约翰·冯·诺伊曼(John von Neumann)(
德语 )的“
量子力学的数学基础 ”。 我们还知道,图灵在1935年接受了剑桥物理学家
拉尔夫·福勒 (
Ralph Fowler)的一项有关量子力学研究的任务。 (福勒提出计算
水的
介电常数 ,这实际上是一个非常困难的任务,需要使用相互作用的量子场理论进行全面分析,但仍不能完全解决)。
然而,图灵何时,如何获得他的狄拉克著作的副本? 考虑到这本书的价格很低,图灵据称购买了已经使用过的书。 谁是这本书的第一任所有者? 书中的注释似乎主要与逻辑结构有关,应注意某些逻辑关系应被视为公理。 那么第127页上的注释又如何呢?
好吧,这可能是一个巧合,但仅在第127页上-狄拉克(Dirac)讨论
了最小作用的量子
原理,并为
费曼路径上的
积分奠定了基础-这是所有现代量子形式主义的基础。 笔记包含什么? 它包含方程式14的扩展,方程式14是量子幅度随时间变化的方程式。 注释的作者用ρ代替了Dirac A的振幅,可能反映了更早的德国(液体密度分析)德国记录。 然后,作者尝试以power(
普朗克常数除以2π的幂,有时也称为
狄拉克常数 )的幂展开作用。
但是从页面上所包含的内容来看,似乎几乎没有什么有用的知识。 如果您将页面保持在明亮状态,它会带来一个小惊喜-标有“ Z f。 理疗。 化学 B”:

这是
德国物理化学杂志ZeitschriftfürPhyskalische Chemie,Abteilung B的删节版本,自1928年以来已出版。 也许这条注释是由期刊编辑写的? 这是1933年的杂志名称。 方便地列出了编辑器及其位置,其中一位脱颖而出:“ Born·Cambridge”。

这是
马克斯·伯恩 (
Max Bourne) ,他是
伯恩规则的作者,更是量子力学理论(以及歌手
奥利维亚·牛顿·约翰 (
Olivia Newton-John )的祖父)的作者。 那么,此注释可能是由Max Born写的吗? 但是,不幸的是,事实并非如此,因为笔迹不匹配。
那第231页的书签呢? 这是从两个方面来看的:

书签很奇怪而且很漂亮。 但是它是什么时候制成的?
剑桥有
一家Heffers书店 ,尽管它现在是Blackwell的一部分。 书签显示,在过去的70多年中(直到1970年),Heffers一直位于该地址,即
Petty Cury的 3和
4 。
此选项卡包含一个重要键-这是电话号码“ Tel。 862。” 事实证明,在1939年,剑桥的大多数地区(包括Heffers)都改用四位数的号码,当然,到1940年,书签上都印有“现代”电话号码。 (英语电话号码逐渐变长;当我在1960年代在英国长大时,我们的电话号码是Oxford 56186和Kidmore End2378。在某种程度上,我记得这些数字是因为,奇怪的是,现在看起来没什么,我在接听电话时总是打我的电话)。
这种形式的书签一直印刷到1939年。 但是在那之前多长时间? 至少自1912年以来,您就可以在Internet上找到很多旧的Heffers广告扫描(以及“我们要求您满足您的要求...”),它们添加了“ Phone 862”,并添加了“(2行)”。 自1904年以来,在书本中还可以找到一些具有类似设计的书签(尽管目前尚不清楚它们是否是这些书的原始书(即同时印刷)。就我们的调查而言,似乎可以得出结论:这本书来自Heffers商店(顺便说一下,这是剑桥的主要书店)在1930年至1939年之间的某个时候。
具有lambda演算的页面
因此,现在我们对这本书的购买时间有所了解。 但是“ lambda演算页面”呢? 这是什么时候写的? 好吧,当然,到那时,λ演算应该已经发明了。 这是由
普林斯顿大学的数学家
阿隆佐·丘奇 (
Alonzo Church )完成的,其最初形式是1932年,最终形式是1935年。 (他们的前任科学家有一些作品,但是他们没有使用符号λ)。
艾伦·图灵与lambda演算之间存在复杂的关系。 1935年,图灵对数学运算的“机械化”产生了兴趣,并发明了使用图灵机解决数学基础问题的想法。 图灵向法国杂志(
Comptes rendus )发送了有关此主题的文章,但在邮件中丢失了。 结果证明,他寄给她的收件人仍然不在,因为他已经搬到了中国。
但是在1936年5月,甚至在图灵可以将他的文章发送到其他地方之前,
阿隆佐·丘奇的
工作都来自美国 。 , 1934
, , ,
1922 .
, - , (
- ). (
) , , . 1936 ( )
« …» .
: 1936 1938 ( 1937 ) , , . , -, —
, - , — , , .
1938 ,
, -, , . 1945 ,
. 1947–8 , ,
.
1951
. ( , , , , - , ). , 1954
, : «
» ( : «
, »). , , 7 1954 , . ( , , .)
, -. , :

, , , . ? ,
, , Spalding&Hodge, Papermakers, « », - , -, . , , , Excelsior, , 1890- 1954 .
?

因此,让我们仔细看一下叶子两边的内容。 让我们从lambdas开始。
这是定义
“纯”或“匿名”函数的一种方法,它们是数学逻辑以及函数编程中的基本概念。 这些功能在
Wolfram语言中非常常见,它们的工作也很容易解释。 例如,有人写
f [
x ]表示应用于参数x的函数
f 。 并且有许多名为
f的函数,例如
Abs或
Sin或
Blur 。 但是,如果有人希望
f [
x ]为
2x +1怎么办? 此功能没有即时名称。 但是还有另一种赋值形式
f [
x ]吗?
答案是肯定的:不是
f而是我们编写
Function[a,2a+1] 。 在Wolfram
Function [a,2a+1][x]语言
Function [a,2a+1][x]将函数应用于自变量x,结果是
2x+1 。
Function[a,2a+1]是“纯”或“匿名”函数,它是2乘以1的纯运算。
因此,λ演算中的λ是Wolfram语言中
Function的精确类似物-因此,例如λa
。(2 a +1)等于
Function[a, 2a + 1] 。 (值得注意的是,该函数,例如
Function[b,2b+1]等效的;“相关变量”
a或
b只是替换该函数的参数的位置-在Wolfram语言中,可以通过使用替代选项来定义纯函数来避免它们
(2# +1)& )。
在传统数学中,函数通常被视为显示输入数据(例如,整数)和输出数据(例如,也是整数)的对象。 但是这个
功能对象(或λ)是什么? 本质上,这是一个结构运算符,它接受表达式并将其转换为函数。 就传统的数学和数学写作形式而言,这似乎有些奇怪,但是如果有人需要操纵任意字符,这会自然得多,即使起初看起来有点抽象。 (应该指出的是,当用户学习Wolfram语言时,我总是可以说,他们在了解
功能时已经克服了抽象思维的一定门槛)。
Lambda只是页面内容的一部分。 还有另一个甚至更抽象的概念-它们是
组合器 。 考虑模糊的
PI1IIx系列吗? 那是什么意思 实际上,这是组合器的序列,或者是符号函数的抽象组成。
Wolfram语言中在数学上非常熟悉的通常的函数叠加形式可以写成:
f[g[x]] -表示“将
f应用于将
g应用于
x的结果”。 但是真的需要括号吗? 在Wolfram中,
f@g@ x是表示法的另一种形式。 在本文中,我们依靠Wolfram语言定义:@运算符与右侧相关联,因此
f@g@x等效于
f@(g@x) 。
但是
(f@g)@x含义是什么? 这等效于
f[g][x] 。 而且,如果
f和
g是数学上的普通函数,那将毫无意义,但是如果
f是
一个高阶函数 ,则
f[g]本身可以是一个很好地应用于
x的函数 。
请注意,这里仍然有些复杂。 在
f[] -f是一个参数的函数。
f[]等效于编写
Function[a, f[a]][x] 。 但是两个参数
f[x,y]的函数呢? 这可以写成
Function[{a,b},f[a, b]][x, y] 。 但是
Function[{a},f[a,b]]呢? 这是什么 有一个“自由变量”
b ,它简单地传递给函数。
Function[{b},Function[{a},f[a,b]]]将绑定此变量,然后绑定
Function[{b},Function[{a},f [a, b]]][y][x] f[x,y]再次给出
f[x,y] 。 (设置该函数使其具有一个自变量被称为“ currying”,以纪念名为
Haskell Curry的科学家逻辑学家)。
如果存在自由变量,即在如何定义函数方面存在许多不同的困难,但是如果我们将自己限制在不具有自由变量的
Function或λ对象上,则基本上可以自由设置它们。 这样的对象称为组合器。
组合器历史悠久。 众所周知,它们最初是由
David Gilbert的门徒
Moses Schoenfinkel于1920年提出
的 。
当时,直到最近才发现您不需要使用
And ,
Or和
Not表达式来表示标准命题逻辑中的表达式:使用唯一的运算符就足够了,我们现在将其称为
Nand (例如,如果我们将
Nand编写为·,然后
Or[a,b]的形式为
(a·a)·(b·b) )。 Schönfinkel希望找到谓词逻辑或本质上包括功能的逻辑的最小表示形式。
他提出了两个“组合符” S和K。在Wolfram语言中,其写为
K [x _] [y_]→x和S [x _] [y _] [z_]→x [z] [y [z]]。
值得注意的是,可以使用这两个组合器来执行任何计算。 所以举个例子
S [K [S]] [S [K [S [K [S]]]] [S [K [K]]]]
可以用作将两个整数相加的函数。
坦率地说,所有这些都是相当抽象的对象,但是现在我们了解了图灵机和lambda微积分,我们可以看到Schoenfinkel组合器实际上预见了通用计算的概念。 (甚至更值得注意的是,1920年的S和K的定义
非常简单 ,类似于我在1990年代提出的
非常简单的通用图灵机 ,其通用性
在2007年得到了
证明 )。
回到我们的传单和
PI1IIx行。 此处记录的字符是组合器,它们都旨在定义功能。 这里的定义是,函数的叠加应该是左联想的,因此
fgx不应解释为f @ g @ x或f @(g @ x)或f [g [x]],而应解释为(f @ g )@x或f [g] [x]。 我们将把该条目转换为Wolfram语言方便使用的格式:
PI1IIx将采用
p [i] [one] [i] [i] [x]的形式 。
为什么要写这样的东西? 为了对此进行解释,我们需要讨论教堂编号(以阿隆佐教堂的名字命名)的概念。 假设我们只使用符号,lambda或组合器。 有没有办法使用它们来指定整数?
只说数字
n对应于
Function[x, Nest[f,x,n]]怎么样? 或者,换句话说,(用简写):
1是
f[#]&2是
f[f[#]]&3是
f[f[f[#]]]&等。
所有这些看起来似乎都比较晦涩,但是之所以引起人们的兴趣是因为它使我们能够完全用符号和抽象来做所有事情,而不必明确地谈论整数。
使用这种指定数字的方法,例如,设想将两个数字相加:3可以表示为
f[f[f[#]]]&而2是
f[f[#]]& 。 您可以简单地通过将其中一个应用到另一个来添加它们:
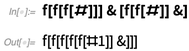
但是
f是什么
样的 ? 可能是任何东西! 在某种意义上,“转到lambda”结尾,并使用以
f作为参数的函数表示数字。 换句话说,将3想象为
Function[f,f[f[f[#]]] &]或
Function[f,Function[x,f[f[f[x]]]] 。 (何时以及如何命名变量是lambda演算中的难题)。
考虑一下图灵在1937年发表的论文《
可计算性和λ-扩散性》中的一个片段,该片段按照我们刚刚讨论的那样设置对象:

在这里,录制可能会有些混乱。 图灵的
x是我们的
f ,而他的
x' (合成器由于插入空格而出错)是我们的
x 。 但是这里使用了完全相同的方法。
因此,让我们看一下叶子前折后的那条线。 这是
I1IIYI1IIx 。 根据Wolfram语言的形式,这将是
i[one][i][i][y][i][one][i][i][x] 。 但是这里我是一个相同的函数,因此
i[one]仅返回
一个 。 同时,
一个是Church对1或
Function[f,f[#]&]的数字表示。 但是使用此定义,
one[]成为
a[#]& ,
one[a][b]成为
a[b] 。 (顺便说一下,
i[][b]或
Identity[][b]也是
[b] )。
如果我们写下
i和
one的替换规则,而不是直接使用lambda微积分,将会更加清楚。 结果将是相同的。 明确应用这些规则,我们得到:

这与第一个缩写记录中呈现的内容完全相同:
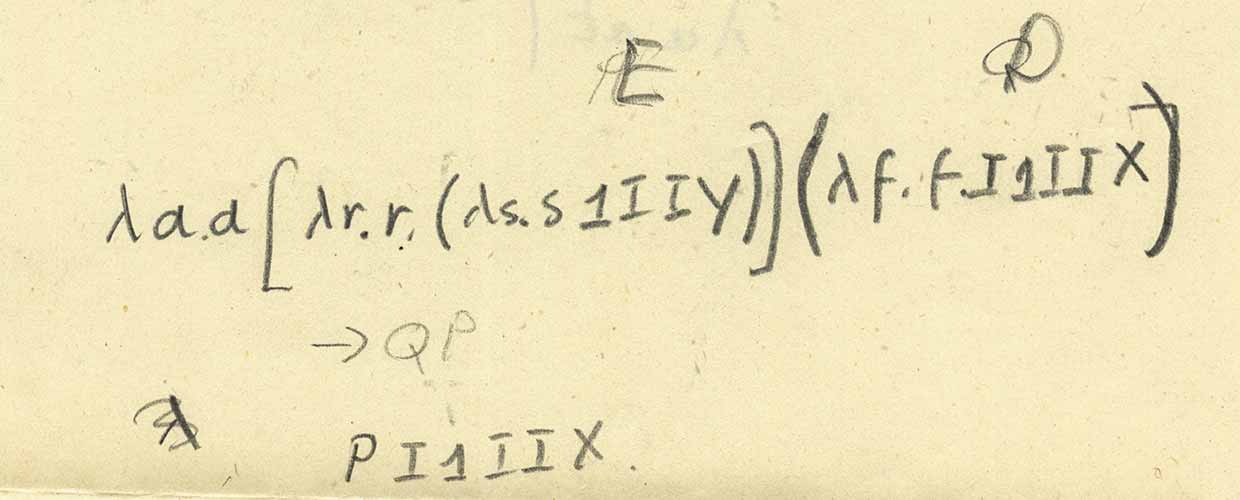
现在,让我们在叶的顶部再次查看:
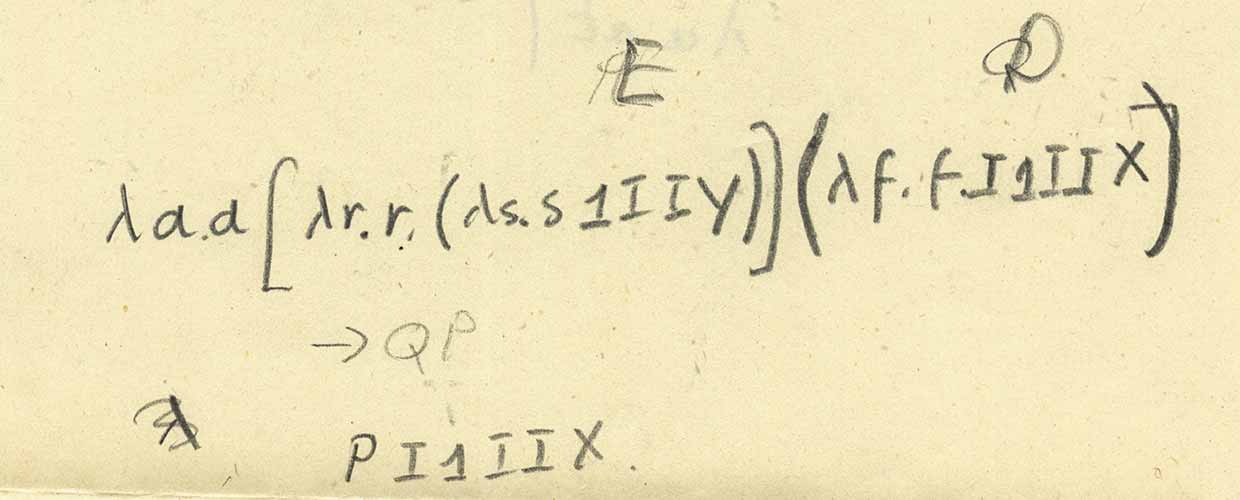
这里有相当混乱和难以理解的对象“ E”和“ D”,但它们的意思是“ P”和“ Q”,因此我们可以写出表达式并计算它(请注意,这里-与最后一个混淆符号-“神秘科学家”用[...]和(...)代表应用程序功能):

因此,这是显示的第一个缩写。 要了解更多,让我们用定义代替Q:

我们得到以下确切的缩写。 如果用表达式代替P会发生什么?
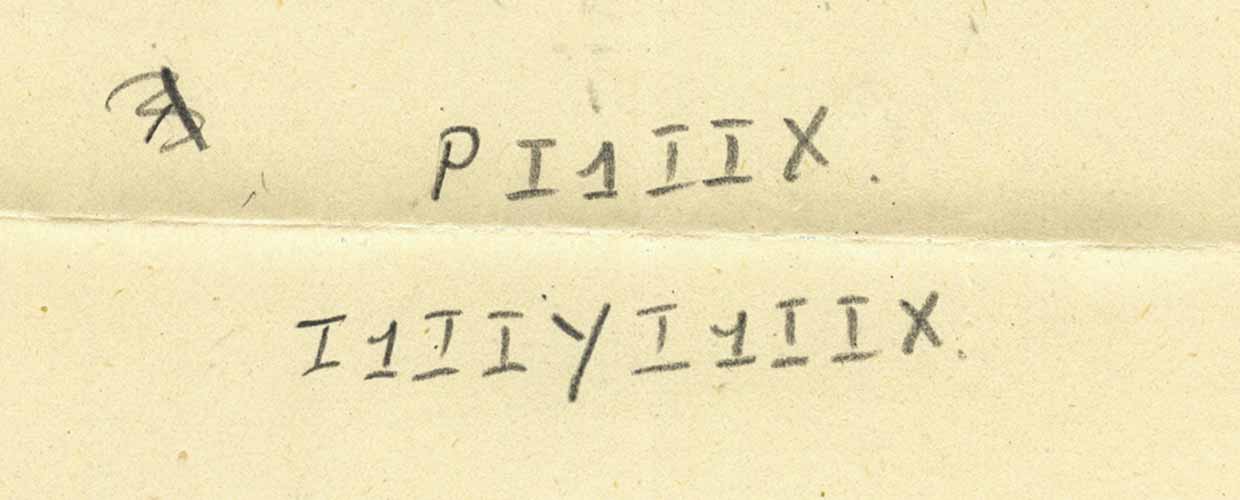
结果如下:

现在,利用i是输出参数本身的函数这一事实,我们得到:

哎呀! 但这不是下一个记录的行。 这里有错吗? 不清楚。 因为,最后,与大多数其他情况不同,没有箭头指示下一行从上一行开始。
这是一个谜,但让我们继续到传单的底部:

这里的2是教堂号码,例如由模式
two[a_] [b_] → a[a[b]] 。 请注意,如果将a视为
Function[r,r[]] ,将
b视为
q ,则实际上这是第二行的形式。 因此,我们希望计算结果如下:

不过,位于内部的表达式
[b]可以写为x(可能与以前写在工作表上的x不同)-结果,我们得到了最终结果:

因此,我们可以破译这片叶子上发生的一些事情,但是至少剩下的一个谜语就是Y应该是什么。
实际上,组合逻辑具有标准的Y组合器:所谓
的定点组合器 。 形式上,它是由以下事实定义的:Y [
f ]必须等于
f [Y [
f ]],或者换句话说,当应用f时Y [
f ]不会改变,因此这是
f的固定点。 (Y组合器与Wolfram语言中的
#0关联。)
当前,由于
启动加速器Y-Combinator ,即所谓的
Paul Graham (长期以来一直是
函数式编程和
LISP编程语言的拥护者,并基于该语言实现了第一个网络商店),Y-combinator变得著名。 他曾经亲自告诉我:“
没人知道Y是一个组合器 。” (应注意,Y Combinator正是使公司避免定点操作的原因...)
Y组合器(像定点组合器)被发明了好几次。 Turing确实在1937年提出了它的实现,他称之为Θ。 但是,我们页面上的字母“ Y”是著名的定点组合器吗? 也许不是。 那么我们的“ Y”是什么? 考虑这种减少:
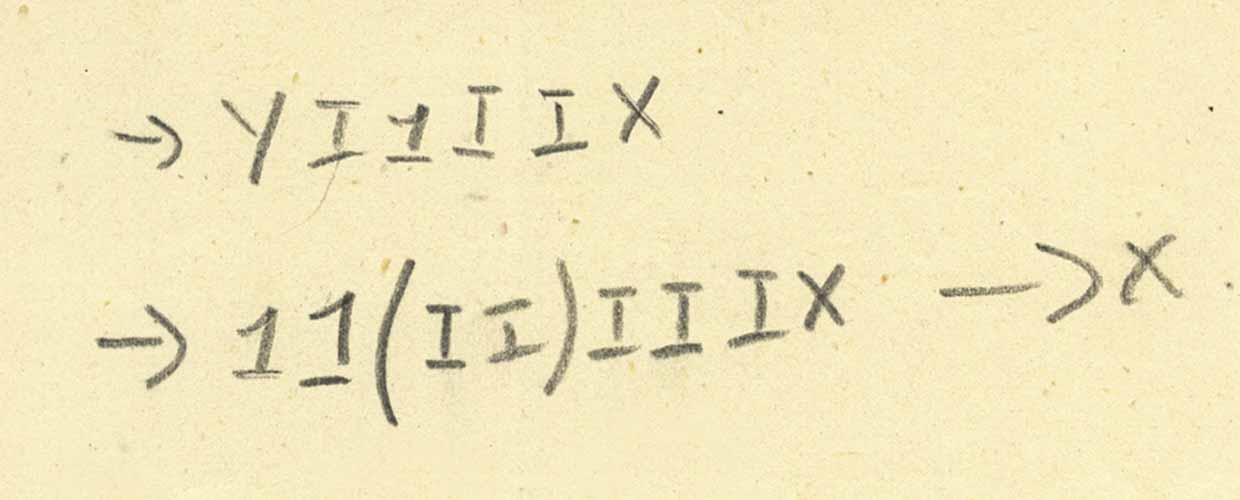
但是,这些信息显然不足以明确确定Y是什么。 看来问题至少是两个论点,但(至少对我来说)尚不清楚要输入多少个论据以及它要做什么。
最后,尽管我们可以理解传单的许多部分,但我们必须说,在全球范围内尚不清楚该传单的内容。 即使需要对工作表中的内容进行很多解释,它在lambda微积分和使用组合器中还是很基本的。
大概是在尝试创建一个简单的“程序”-使用lambda微积分和组合器来做某事。 但是,就逆向工程的典型情况而言,我们很难说出这个“东西”应该是什么以及一个共同的“可解释的”目标是什么。
工作表上还有另一个功能,在这里值得一提-使用各种类型的括号。 在传统数学中,括号主要用于所有内容-函数的应用(如
f(x) )和成员分组(如
(1 + x)(1-x) ,或者不太明显的是
a(1- x) )。 (在Wolfram语言中,我们将方括号的各种用法分开使用-在方括号中定义
f [x]函数-括号仅用于分组)。
当lambda演算第一次出现时,关于方括号的使用存在很多问题。 后来,艾伦·图灵(Alan Turing)撰写了整本书(未出版),标题为“
转变符号和词组的数学形式 ”,但早在1937年,他就已经意识到他需要描述lambda微积分的现代(确切地说是黑客)定义(顺便说一句,为教会)。
他说适用于
g的 f应该写为
{f}(g) ,除非
f是唯一字符,在这种情况下可能是
f(g) 。 然后,他说lambda(如
Function[a, b] )应写为λa [
b ]或替代地写为λa。
b 。
但是,也许到1940年,使用{...}和[...]来表示不同对象的整个想法被废弃了,主要是赞成使用标准数学样式的方括号。
看一下页面顶部:

以这种形式,很难理解。 在教会的定义中,方括号用于分组,用方括号代替句点。 使用此定义,可以很清楚地看到,Q(最终标记为D)最后加上括号,是整个初始lambda所适用的。
实际上,此处的方括号并不限制lambda的主体; 相反,它实际上表示该函数的另一个应用程序,并且没有明确表示lambda主体在何处结束。 最后,可以看出,“神秘科学家”将右方括号更改为一个圆括号,从而有效地应用了Church的定义-并迫使他计算表达式,如表所示。
那么,这小块到底意味着什么? 我认为这表明该页面是在1930年代写的,或者此后不久就写了,因为括号的传说还没有定下来。
那是谁的笔迹呢?
因此,在此之前,我们讨论了页面上写的内容。 但是写那封信的人又如何呢?
最明显的候选人是艾伦·图灵(Alan Turing)本人,因为毕竟该页面在他的书中。 就内容而言,似乎没有什么与阿兰·图灵可以写这篇文章的事实相矛盾的,即使是在他于1936年初收到丘奇的文章后首次开始处理λ演算的那一刻。
手写呢? 它属于艾伦·图灵吗? 考虑几个尚存的样本,正如我们确定的那样,这些样本是由Alan Turing编写的:
所呈现的文本看上去很不相同,但是文本中使用的符号又如何呢? 至少在我看来,这看起来并不那么明显-可以假设任何差异都可以由以下事实造成:写在档案库中的现有样本(可以说“完成”),而我们的样本一页是思想工作的反映。
事实证明,对于我们的调查来说很方便,在Turing档案中有一个页面,他在页面上写下了表示法所需
的字符表 。 当逐个字母地比较这些字符时,它们看起来与我非常相似(这些记录是在图灵当时
研究植物生长的
时候记录
下来的 ,因此出现了“叶子区域”字样):

我想对此进行更深入的研究,所以我将样本发送给了专业的笔迹专家(兼笔迹作者)
希拉·洛 (
Sheila Lowe ),我见过一次面-只是将我们的图纸作为“样本A”出示,而将现有的图灵笔迹作为“样品”“ B”。 她的回答是最终的和否定的:“
写作风格完全不同。 至于人格,样本“ B”的作者比样本“ A ”
的作者具有更快,更直观的思维方式 。”
我还没有完全相信这一点,但决定是时候寻找其他选择了。
因此,如果事实证明图灵没有写这个,那是谁做的? 诺曼·鲁特里奇(Norman Rutledge)告诉我,他从图灵的执行者罗宾·甘地(Robin Gandhi)那里收到了这本书。 因此,我从甘地寄出了“样品” C“”:

但是希拉的初步结论是,这三个样本可能是由三个不同的人撰写的,再次指出样本“ B”是从“
最快的思想家-最有可能最愿意寻找问题的非常规解决方案的人 ”获得的。 。 (考虑到图灵在1920年代的学校作业中的每个人都非常积极地抱怨他的笔迹,我很高兴现代的笔迹专家会对图灵的笔迹进行这样的评估)。
好吧,那一刻,图灵和甘地似乎都被排除在“嫌疑犯”名单之外。 那么谁能写这个? 我开始想到图灵可以借给他的书的人。 当然,同时,他们应该能够使用Lambda微积分进行计算。
考虑到纸上的水印,我建议该人应该是剑桥人,或者至少是英国人。 我误以为是在1936年左右才是写这篇文章的正确时机。 那么他当时认识谁?图灵与谁进行了交流? . ( 13 , 1930 1936 .)
. , , , — 1933 ,
(«» ) : 0.12345678910111213… (
1, 2, 3, 4 ,…, 8, 9, 10, 11, 12,…, ,
«» , ).
1937 - , ,
. ( , - ).
,
( ) , . ( , 1948
Turbochamp — , , ).
? LinkedIn, , , Microsoft. , , . ( ):

, ( f . .)
?
, . «
», , . ( , , , , ,
).
— , .
«»
, . , , , , , .
, -, ? 1946 (, ). 1949 , . 1954 , . , 1957 . , (, , , , . .). 1960 , ( ) ( ), , .
? - (, , , 2005 , «»). , « ».
- , , , ? . , - - - . , 1955 « » ( ,
BooleanMinimize ). , ( «NAR», «NAR…», , «NARLAB» — «» ). .
. , , , «
». , , , , 1954 , . , , .
, «
( , ) » «
, , , , [ ] ». , ?
. ( , , , 1902 , « » : «
»).
, , , ,
, 12 , -, , , 21 ).
, , - . ,
- . , , , 1938 . 2000 -
( ) — , , 2002 , .
, , ? , , . :

, . , , , , , .
:
? , , , .
- , — 1940 — . , 1944 , , . , , .
, , , , 1952 ,
« » . , , , , — , , .
, . , , , , . ,
1980- , “ » — , , , . ( , , , , «
, »). , «
, , , — … », , «
».)
, , . . , «
» (. . -), -.
. 1969 , , , , , .
, , . . — — .
. - , , .
1995 , .
—
. . , , — , , , . , , ,
, , 24 . (
2001 — 45 ).
, ? , , , , ,
( , ,
, c ). (
) « » ( ), , -, , . , .
, . , 30 , . , , , - — , , , (, , ,
Mathematica ). , , , , , , , . , , , .
? , , () , . ( , .) , 1 . , .
, , . : «
! » , . . , -, , , .
, , , , , . , :
. ; .
, . , ? - , 1930- . , , , - 1940- . , . , , , , , -.
, - , , , . , , , , , , .
, , — , , …: ( ), ( ) ( ).
Wolfram Language?
.
新课程注册 。 准备在线课程 。
Wolfram Language.