🤯 🀄️ 📊 求解简单线性回归方程 🙏🏻 🙋🏻 🤾🏼

本文讨论了确定简单（成对）回归线数学方程的几种方法。

此处讨论的所有方程求解方法均基于最小二乘法。我们将这些方法表示如下：

分析溶液
梯度下降
随机梯度下降

对于解决直线方程的每种方法，本文介绍了各种函数，这些函数主要分为不使用NumPy库编写的函数和使用NumPy进行计算的函数。 NumPy的熟练使用被认为可以减少计算成本。

本文中的所有代码都是使用Jupyter Notebook用python 2.7编写的。源代码和示例数据文件发布在github上

本文主要针对初学者和已经开始精通人工智能（机器学习）非常广泛的部分研究的人们。

为了说明材料，我们使用一个非常简单的示例。

示例条件

我们有五个值来表征Y对X的依赖性（表1）：

表1“示例的条件”

我们假设值

$x_i$ 是一年中的月份，并且

$y_i$ -本月收入。换句话说，收入取决于一年中的月份，并且

$x_i$ -收入依赖的唯一标志。就收入在一年中月份的条件依赖性以及价值的数量而言，都是这样的一个例子。它们很少。但是，这种简化将使手指所指的东西（并非总是如此）能够轻松地解释初学者所吸收的材料。而且，数字的简单性将使那些希望在纸上解决该示例的人员无需花费大量的人工成本。假设示例中显示的依赖关系可以通过以下形式的简单（成对）回归线的数学方程很好地近似：

$Y = a + bx$ 在哪里

$x$ -这是收到收入的月份，

$Y$ -相应月份的收入，

一

$一$ 和

$b$ -估计线的回归系数。注意系数

$b$ 通常称为估算线的斜率或坡度；代表改变的数量

$Y$ 改变时

$x$ 。显然，我们在示例中的任务是在方程式中选择此类系数

一

$一$ 和

$b$ 为此，我们估算的每月收入与真实答案之间的偏差，即样本中显示的值将是最小的。

最小二乘法

根据最小二乘法，应通过平方平方来计算偏差。如果偏差具有相反的符号，则这种技术避免了偏差的相互补偿。例如，如果在一种情况下，偏差为+5 （加5），而在另一种情况下，偏差为-5 （负5），则偏差的总和将相互补偿并为0（零）。您不能浪费偏差，但可以使用模块属性，然后所有偏差将为正并累积在我们内部。我们将不详细讨论这一点，而只是指出为了方便计算，通常对偏差进行平方。这是公式的外观，我们可以借助该公式确定最小的平方偏差（误差）之和：

$ERR（x）= \ sum \ limit_ {i = 1} ^ n（a + bx_i-y_i）^ 2 = \ sum \ limits_ {i = 1} ^ n（f（x（i）-y_i）^ 2 \ rightarrow分钟$ 在哪里

$f（x_i）= a + bx_i$ 是近似真实答案（即我们计算的收入）的函数，

$y_i$ -这些是正确答案（示例中提供的收入），

$我$ 是样本索引（确定偏差的月份数）我们对函数进行微分，定义偏微分方程，并准备进行解析。但首先，让我们简短地讨论一下微分是什么，并回顾一下导数的几何含义。

差异化

微分是找到一个函数的导数的操作。导数是什么？函数的导数表征函数的变化率并指示其方向。如果给定点的导数为正，则函数增加，否则，函数减小。导数模的值越大，函数值的变化率就越高，并且函数图的角度越陡。例如，在笛卡尔坐标系的条件下，在点M（0,0）等于+25的导数的值表示在给定点将值移动

$x$ 任意单位的权利，价值

$y$ 增加25个常规单位。在图中，它看起来像一个相当陡峭的仰角

$y$ 从给定的角度来看。另一个例子。微分值-0.1表示偏移时

$x$ 每常规单位价值

$y$ 仅减少0.1常规单位。同时，在功能图上，我们可以看到几乎没有明显的向下倾斜。与山脉相似，我们似乎是缓慢地从山脉缓缓下坡，与前面的示例不同，我们必须经过非常陡峭的山峰:)因此，在区分功能之后

$ERR（x）= \ sum \ limits_ {i = 1} ^ n（a + bx_i-y_i）^ 2$ 按系数

$一$ 和

$b$ ，我们定义了一阶偏导数的方程。在定义方程式之后，我们得到一个由两个方程式组成的系统，决定我们可以选择这样的系数值

$一$ 和

$b$ 在给定点上，相应的导数的值会改变非常小的值，而对于解析解，它们根本不会改变。换句话说，在找到的系数处的误差函数达到最小值，因为在这些点处的偏导数的值为零。因此，根据微分规则，关于系数的一阶偏导数方程

$一$ 将采用以下形式：

$2na + 2b \ sum \ limits_ {i = 1} ^ nx_i-2 \ sum \ limits_ {i = 1} ^ ny_i = 2（na + b \ sum \ limits_ {i = 1} ^ nx_i-\ sum \ limits_ {i = 1} ^ ny_i）$ 关于的一阶偏微分方程

$b$ 将采用以下形式：

$2a \ sum \ limits_ {i = 1} ^ nx_i + 2b \ sum \ limits_ {i = 1} ^ nx ^ 2_i-2 \ sum \ limits_ {i = 1} ^ nx_iy_i = 2 \ sum \ limits_ {i = 1} ^ nx_i（a + b \ sum \ limits_ {i = 1} ^ nx_i-\ sum \ limits_ {i = 1} ^ ny_i）$ 结果，我们得到了一个具有相当简单的解析解的方程组：\开始{equation *}\开始{cases}na + b \ sum \ limits_ {i = 1} ^ nx_i-\ sum \ limits_ {i = 1} ^ ny_i = 0\\\ sum \ limits_ {i = 1} ^ nx_i（a + b \ sum \ limits_ {i = 1} ^ nx_i-\ sum \ limits_ {i = 1} ^ ny_i）= 0\结尾{cases}\ end {equation *}在求解方程式之前，请预加载，检查正确的加载并格式化数据。

下载并格式化数据

应该注意的是，由于对于解析解决方案以及后来的梯度下降和随机梯度下降，我们将使用两种形式的代码：使用NumPy库和不使用它，我们将需要相应地格式化数据（请参见代码）。

下载和数据处理代码

#      import pandas as pd import numpy as np import matplotlib.pyplot as plt import math import pylab as pl import random #    Jupyter %matplotlib inline #    from pylab import rcParams rcParams['figure.figsize'] = 12, 6 #   Anaconda import warnings warnings.simplefilter('ignore') #   table_zero = pd.read_csv('data_example.txt', header=0, sep='\t') #         print table_zero.info() print '********************************************' print table_zero print '********************************************' #     NumPy x_us = [] [x_us.append(float(i)) for i in table_zero['x']] print x_us print type(x_us) print '********************************************' y_us = [] [y_us.append(float(i)) for i in table_zero['y']] print y_us print type(y_us) print '********************************************' #     NumPy x_np = table_zero[['x']].values print x_np print type(x_np) print x_np.shape print '********************************************' y_np = table_zero[['y']].values print y_np print type(y_np) print y_np.shape print '********************************************'

可视化

现在，首先下载数据，然后检查正确的加载并最终格式化数据，然后进行第一次可视化。通常，使用Seaborn库的pairplot方法。在我们的示例中，由于数量有限，因此使用Seaborn库没有任何意义。我们将使用常规的Matplotlib库 ，仅查看散点图。

散点图代码

 print ' №1 "    "' plt.plot(x_us,y_us,'o',color='green',markersize=16) plt.xlabel('$Months$', size=16) plt.ylabel('$Sales$', size=16) plt.show()

附表1“收入在一年中的依赖情况”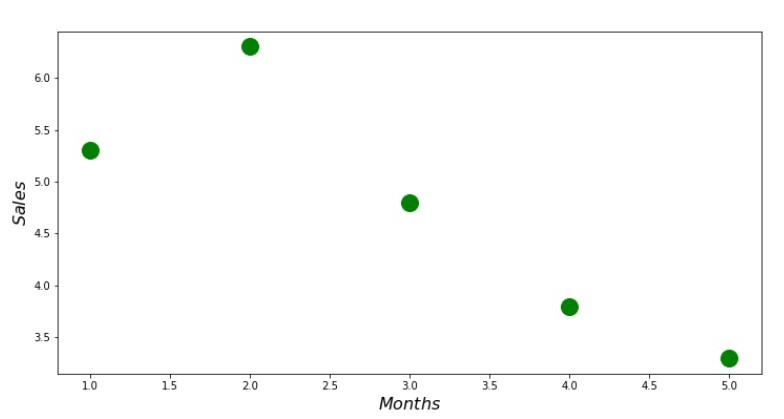

分析溶液

我们将使用python中最常用的工具并求解方程组：\开始{equation *}\开始{cases}na + b \ sum \ limits_ {i = 1} ^ nx_i-\ sum \ limits_ {i = 1} ^ ny_i = 0\\\ sum \ limits_ {i = 1} ^ nx_i（a + b \ sum \ limits_ {i = 1} ^ nx_i-\ sum \ limits_ {i = 1} ^ ny_i）= 0\结尾{cases}\ end {equation *}根据Cramer的规则，我们可以找到一个共同的行列式和行列式

$一$ 和

$b$ ，然后将行列式除以

$一$ 在共同的行列式上-我们找到系数

$一$ ，类似地，找到系数

$b$ 。

分析解决方案代码

 #      a  b    def Kramer_method (x,y): #   ( ) sx = sum(x) #    (   ) sy = sum(y) #       list_xy = [] [list_xy.append(x[i]*y[i]) for i in range(len(x))] sxy = sum(list_xy) #    list_x_sq = [] [list_x_sq.append(x[i]**2) for i in range(len(x))] sx_sq = sum(list_x_sq) #   n = len(x) #   det = sx_sq*n - sx*sx #   a det_a = sx_sq*sy - sx*sxy #   a a = (det_a / det) #   b det_b = sxy*n - sy*sx #   b b = (det_b / det) #   () check1 = (n*b + a*sx - sy) check2 = (b*sx + a*sx_sq - sxy) return [round(a,4), round(b,4)] #       ab_us = Kramer_method(x_us,y_us) a_us = ab_us[0] b_us = ab_us[1] print '\033[1m' + '\033[4m' + "   a  b:" + '\033[0m' print 'a =', a_us print 'b =', b_us print #        def errors_sq_Kramer_method(answers,x,y): list_errors_sq = [] for i in range(len(x)): err = (answers[0] + answers[1]*x[i] - y[i])**2 list_errors_sq.append(err) return sum(list_errors_sq) #       error_sq = errors_sq_Kramer_method(ab_us,x_us,y_us) print '\033[1m' + '\033[4m' + "  " + '\033[0m' print error_sq print #    # print '\033[1m' + '\033[4m' + "     :" + '\033[0m' # % timeit error_sq = errors_sq_Kramer_method(ab,x_us,y_us)

这是我们得到的：

因此，找到系数值，设置偏差平方和。根据找到的系数，我们在散射直方图中绘制一条直线。

回归行代码

 #         def sales_count(ab,x,y): line_answers = [] [line_answers.append(ab[0]+ab[1]*x[i]) for i in range(len(x))] return line_answers #   print '№2 "   "' plt.plot(x_us,y_us,'o',color='green',markersize=16, label = '$True$ $answers$') plt.plot(x_us, sales_count(ab_us,x_us,y_us), color='red',lw=4, label='$Function: a + bx,$ $where$ $a='+str(round(ab_us[0],2))+',$ $b='+str(round(ab_us[1],2))+'$') plt.xlabel('$Months$', size=16) plt.ylabel('$Sales$', size=16) plt.legend(loc=1, prop={'size': 16}) plt.show()

附表2“正确和估计的答案”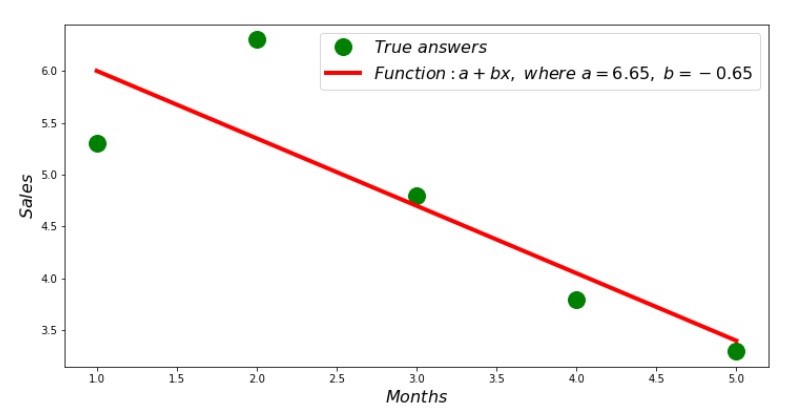

您可以查看每个月的偏差时间表。在我们的案例中，我们不能从中获得任何重大的实际价值，但我们会满足以下好奇心：简单的线性回归方程可以很好地描述当年收入对收入的依赖性。

偏差时间表代码

 #         def error_per_month(ab,x,y): sales_c = sales_count(ab,x,y) errors_percent = [] for i in range(len(x)): errors_percent.append(100*(sales_c[i]-y[i])/y[i]) return errors_percent #   print '№3 " -, %"' plt.gca().bar(x_us, error_per_month(ab_us,x_us,y_us), color='brown') plt.xlabel('Months', size=16) plt.ylabel('Calculation error, %', size=16) plt.show()

附表3“偏差，％”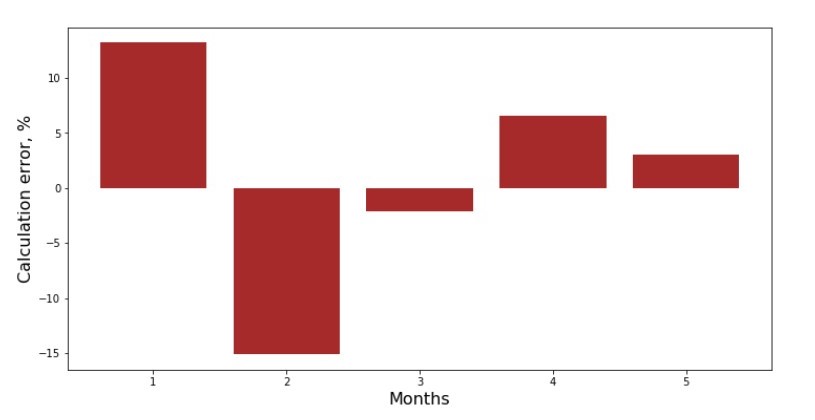

并不完美，但是我们完成了任务。我们编写了一个函数，用于确定系数

$一$ 和

$b$ 使用NumPy库，更准确地说，我们将编写两个函数：一个使用伪逆矩阵（由于过程复杂且不稳定，因此不建议在实践中使用），另一个使用矩阵方程式。

分析解决方案代码（NumPy）

 #          1. #     ,      a vector_1 = np.ones((x_np.shape[0],1)) x_np = table_zero[['x']].values #         x_np x_np = np.hstack((vector_1,x_np)) #  ,     print vector_1[0:3] print x_np[0:3] print '***************************************' print #  ,     a  b     def pseudoinverse_matrix(X, y): #      X = np.matrix(X) #    XT = XT #    XTX = XT*X #    inv = np.linalg.pinv(XTX) #      y = np.matrix(y) #    return (inv*XT)*y #   ab_np = pseudoinverse_matrix(x_np, y_np) print ab_np print '***************************************' print #  ,       def matrix_equation(X,y): a = np.dot(XT, X) b = np.dot(XT, y) return np.linalg.solve(a, b) #   ab_np = matrix_equation(x_np,y_np) print ab_np

比较确定系数所需的时间

$一$ 和

$b$ ，按照提出的3种方法进行。

计算时间代码

 print '\033[1m' + '\033[4m' + "       NumPy:" + '\033[0m' % timeit ab_us = Kramer_method(x_us,y_us) print '***************************************' print print '\033[1m' + '\033[4m' + "       :" + '\033[0m' %timeit ab_np = pseudoinverse_matrix(x_np, y_np) print '***************************************' print print '\033[1m' + '\033[4m' + "       :" + '\033[0m' %timeit ab_np = matrix_equation(x_np, y_np)

在少量数据上，出现了一种“自写”功能，该功能使用Cramer方法查找系数。现在您可以继续寻找系数的其他方法

$一$ 和

$b$ 。

梯度下降

首先，让我们定义什么是渐变。以简单的方式，渐变是指示函数最大增长方向的片段。用与上坡类似的爬升类推，是到达山顶的最陡峭的爬升。以山区为例，我们记得实际上我们需要最陡峭的下降以便尽快到达低地，即最小值-函数不增加或减少的地方。此时，导数将为零。因此，我们不需要渐变，而是反渐变。要找到反梯度，您只需要将梯度乘以-1 （减一）即可。我们提请注意以下事实：一个函数可以有多个最小值，并且根据下面提出的算法归入其中一个最小值，我们将无法找到另一个最小值，该最小值可能低于找到的最小值。放松，我们没有危险！就我们而言，由于我们的职能是

$\ sum \ limits_ {i = 1} ^ n（a + bx_i-y_i）^ 2$ 图上是一个普通的抛物线。众所周知，从数学学校课程中我们可以看到，抛物线只有一个最小值。在我们找到了为什么需要渐变之后，并且渐变是一个片段，即具有给定坐标的向量，它们的系数完全相同

$一$ 和

$b$ 我们可以实现梯度下降。在开始之前，我建议您仅阅读有关下降算法的几句话：

我们以伪随机方式确定系数的坐标 $一$ 和 $b$ 。在我们的示例中，我们将确定系数接近零。这是一种常见的做法，但是每种做法可能都有自己的做法。
从坐标 $一$ 在该点减去一阶偏导数的值 $一$ 。因此，如果导数为正，则函数增加。因此，除去导数的值，我们将朝相反的增长方向移动，即朝下降方向移动。如果导数为负，则此点的函数会减小，并减去导数的值，我们朝着下降方向移动。
我们对坐标进行类似的操作 $b$ ：减去该点的偏导数的值 $b$ 。
为了不跳下最小值并且不飞入较远的空间，必须将步长设置为朝下降方向。通常，您可以撰写整篇文章，内容涉及如何正确设置步长以及如何在下降期间更改步长以减少计算成本。但是现在我们的任务略有不同，我们将通过科学的“戳戳”方法来确定步长，或者，正如他们在普通人中所说的那样，根据经验确定步长。
从给定坐标开始 $一$ 和 $b$ 减去导数的值，我们得到新的坐标 $一$ 和 $b$ 。我们已经从计算出的坐标开始进行下一步（减法）。因此，该循环一次又一次地开始，直到实现所需的收敛为止。

仅此而已！现在，我们准备去寻找马里亚纳海沟最深的峡谷。下来

梯度下降码

 #        NumPy. #       x,y,   ( =0,1),  (tolerance) def gradient_descent_usual(x_us,y_us,l=0.1,tolerance=0.000000000001): #   ( ) sx = sum(x_us) #    (   ) sy = sum(y_us) #       list_xy = [] [list_xy.append(x_us[i]*y_us[i]) for i in range(len(x_us))] sxy = sum(list_xy) #    list_x_sq = [] [list_x_sq.append(x_us[i]**2) for i in range(len(x_us))] sx_sq = sum(list_x_sq) #   num = len(x_us) #   ,    a = float(random.uniform(-0.5, 0.5)) b = float(random.uniform(-0.5, 0.5)) #    ,     1  0 #       errors = [1,0] #    #     ,        ,    tolerance while abs(errors[-1]-errors[-2]) > tolerance: a_step = a - l*(num*a + b*sx - sy)/num b_step = b - l*(a*sx + b*sx_sq - sxy)/num a = a_step b = b_step ab = [a,b] errors.append(errors_sq_Kramer_method(ab,x_us,y_us)) return (ab),(errors[2:]) #    list_parametres_gradient_descence = gradient_descent_usual(x_us,y_us,l=0.1,tolerance=0.000000000001) print '\033[1m' + '\033[4m' + "  a  b:" + '\033[0m' print 'a =', round(list_parametres_gradient_descence[0][0],3) print 'b =', round(list_parametres_gradient_descence[0][1],3) print print '\033[1m' + '\033[4m' + "  :" + '\033[0m' print round(list_parametres_gradient_descence[1][-1],3) print print '\033[1m' + '\033[4m' + "    :" + '\033[0m' print len(list_parametres_gradient_descence[1]) print

我们跌至马里亚纳海沟的最底端，在那里我们发现所有相同的系数值

$一$ 和

$b$ ，实际上是可以预期的。让我们再潜水一次，只是这次，我们的深海飞行器的填充将是其他技术，即NumPy库。

梯度下降码（NumPy）

 #           NumPy, #          NumPy def error_square_numpy(ab,x_np,y_np): y_pred = np.dot(x_np,ab) error = y_pred - y_np return sum((error)**2) #        NumPy. #       x,y,   ( =0,1),  (tolerance) def gradient_descent_numpy(x_np,y_np,l=0.1,tolerance=0.000000000001): #   ( ) sx = float(sum(x_np[:,1])) #    (   ) sy = float(sum(y_np)) #       sxy = x_np*y_np sxy = float(sum(sxy[:,1])) #    sx_sq = float(sum(x_np[:,1]**2)) #   num = float(x_np.shape[0]) #   ,    a = float(random.uniform(-0.5, 0.5)) b = float(random.uniform(-0.5, 0.5)) #    ,     1  0 #       errors = [1,0] #    #     ,        ,    tolerance while abs(errors[-1]-errors[-2]) > tolerance: a_step = a - l*(num*a + b*sx - sy)/num b_step = b - l*(a*sx + b*sx_sq - sxy)/num a = a_step b = b_step ab = np.array([[a],[b]]) errors.append(error_square_numpy(ab,x_np,y_np)) return (ab),(errors[2:]) #    list_parametres_gradient_descence = gradient_descent_numpy(x_np,y_np,l=0.1,tolerance=0.000000000001) print '\033[1m' + '\033[4m' + "  a  b:" + '\033[0m' print 'a =', round(list_parametres_gradient_descence[0][0],3) print 'b =', round(list_parametres_gradient_descence[0][1],3) print print '\033[1m' + '\033[4m' + "  :" + '\033[0m' print round(list_parametres_gradient_descence[1][-1],3) print print '\033[1m' + '\033[4m' + "    :" + '\033[0m' print len(list_parametres_gradient_descence[1]) print

系数值

$一$ 和

$b$ 不变。让我们看看误差在梯度下降过程中是如何变化的，即，平方差的总和随每一步如何变化。

平方偏差总和图的代码

 print '№4 "   -"' plt.plot(range(len(list_parametres_gradient_descence[1])), list_parametres_gradient_descence[1], color='red', lw=3) plt.xlabel('Steps (Iteration)', size=16) plt.ylabel('Sum of squared deviations', size=16) plt.show()

图№4“梯度下降的偏差平方和”

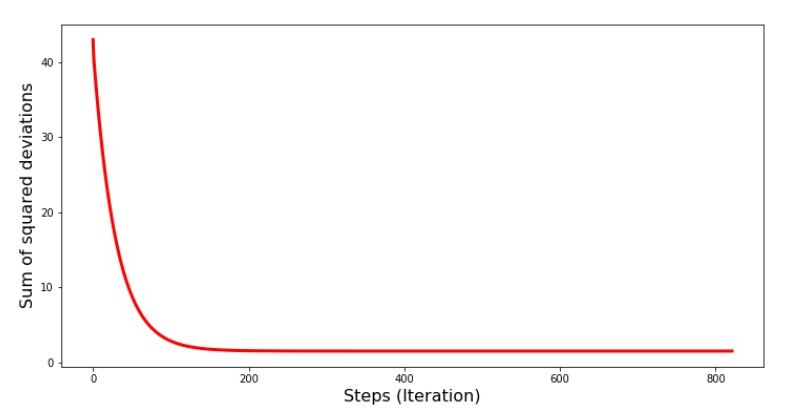
在图上我们看到，每一步的误差都减小了，经过一定数量的迭代，我们观察到了一条实际上的水平线。最后，我们估算代码执行时间的差异：

确定梯度下降计算时间的代码

 print '\033[1m' + '\033[4m' + "       NumPy:" + '\033[0m' %timeit list_parametres_gradient_descence = gradient_descent_usual(x_us,y_us,l=0.1,tolerance=0.000000000001) print '***************************************' print print '\033[1m' + '\033[4m' + "       NumPy:" + '\033[0m' %timeit list_parametres_gradient_descence = gradient_descent_numpy(x_np,y_np,l=0.1,tolerance=0.000000000001)

也许我们做错了，但是同样，一个不使用NumPy库的简单“自写”函数比使用NumPy库的函数提前了。但是，我们不会停滞不前，而是转向研究另一种令人兴奋的方法来求解简单线性回归方程。认识我！

随机梯度下降

为了快速了解随机梯度下降的工作原理，最好确定其与普通梯度下降的区别。在梯度下降的情况下，我们的导数方程为

$一$ 和

$一$ 使用了所有属性的值之和以及样本中可用的真实答案（即所有

$x_i$ 和

$y_i$ ）在随机梯度下降中，我们将不使用样本中所有可用的值，而是以伪随机方式选择所谓的样本索引并使用其值。例如，如果索引是由数字3（三）确定的，那么我们取值

$x_3 = 3$ 和

$y_3 = $ 4.$ ，然后将值代入微分方程式并确定新坐标。然后，在确定坐标之后，我们再次伪随机地确定样本的索引，用偏微分方程替换与索引对应的值，并以新的方式确定坐标

$一$ 和

$一$ 等在绿化收敛之前。乍一看，这似乎可以解决，但确实可以。的确，值得注意的是，误差不会随着每一步的减少而减小，但是趋势肯定存在。随机梯度下降比平时有什么优势？如果我们的样本量非常大并且以成千上万的值进行度量，则处理起来要容易得多，例如，随机抽样一千个样本即可。在这种情况下，将启动随机梯度下降。当然，就我们而言，我们不会注意到很大的不同。我们看一下代码。

随机梯度下降代码

 #   .. def stoch_grad_step_usual(vector_init, x_us, ind, y_us, l): #   ,      ind # (.- stoch_grad_descent_usual) x = x_us[ind] #   y (),     x y_pred = vector_init[0] + vector_init[1]*x_us[ind] #         error = y_pred - y_us[ind] #     ab grad_a = error #    ab grad_b = x_us[ind]*error #     vector_new = [vector_init[0]-l*grad_a, vector_init[1]-l*grad_b] return vector_new #   .. def stoch_grad_descent_usual(x_us, y_us, l=0.1, steps = 800): #          vector_init = [float(random.uniform(-0.5, 0.5)), float(random.uniform(-0.5, 0.5))] errors = [] #    #       (steps) for i in range(steps): ind = random.choice(range(len(x_us))) new_vector = stoch_grad_step_usual(vector_init, x_us, ind, y_us, l) vector_init = new_vector errors.append(errors_sq_Kramer_method(vector_init,x_us,y_us)) return (vector_init),(errors) #    list_parametres_stoch_gradient_descence = stoch_grad_descent_usual(x_us, y_us, l=0.1, steps = 800) print '\033[1m' + '\033[4m' + "  a  b:" + '\033[0m' print 'a =', round(list_parametres_stoch_gradient_descence[0][0],3) print 'b =', round(list_parametres_stoch_gradient_descence[0][1],3) print print '\033[1m' + '\033[4m' + "  :" + '\033[0m' print round(list_parametres_stoch_gradient_descence[1][-1],3) print print '\033[1m' + '\033[4m' + "     :" + '\033[0m' print len(list_parametres_stoch_gradient_descence[1])

我们仔细查看系数，并陷入“如何？”这一问题。我们得到了系数的其他值

$一$ 和

$b$ 。也许随机梯度下降找到了方程的更多最佳参数？ las，不。查看平方偏差的总和就足够了，并且看到有了新的系数值，误差就更大了。不要急于绝望。我们绘制误差变化。

随机梯度下降的平方偏差总和图的代码

 print ' №5 "   -"' plt.plot(range(len(list_parametres_stoch_gradient_descence[1])), list_parametres_stoch_gradient_descence[1], color='red', lw=2) plt.xlabel('Steps (Iteration)', size=16) plt.ylabel('Sum of squared deviations', size=16) plt.show()

图表№5“随机梯度下降中的偏差平方和”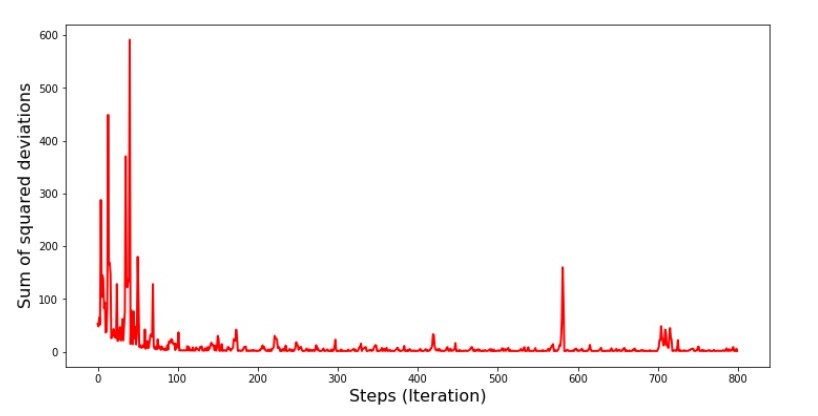

查看时间表后，一切准备就绪，现在我们将修复所有问题。那怎么了以下发生了。当我们随机选择一个月时，我们的算法会针对选定的月份来减少计算收入时的误差。然后我们选择另一个月份并重复计算，但是我们已经减少了所选第二个月的误差。现在让我们回想一下，在最初的两个月中，我们已经大大偏离了简单线性回归方程的直线。这意味着当选择这两个月中的任何一个，然后减少每个月的误差时，我们的算法会严重增加整个样本的误差。那该怎么办呢？答案很简单：您需要减少下降步骤。毕竟，通过减少下降步骤，错误也将停止“跳”上跳下。而是，错误“跳过”不会停止，但不会那么快就完成：)我们将进行检查。

以更少的步骤运行SGD的代码

 #  ,    100       list_parametres_stoch_gradient_descence = stoch_grad_descent_usual(x_us, y_us, l=0.001, steps = 80000) print '\033[1m' + '\033[4m' + "  a  b:" + '\033[0m' print 'a =', round(list_parametres_stoch_gradient_descence[0][0],3) print 'b =', round(list_parametres_stoch_gradient_descence[0][1],3) print print '\033[1m' + '\033[4m' + "  :" + '\033[0m' print round(list_parametres_stoch_gradient_descence[1][-1],3) print print '\033[1m' + '\033[4m' + "     :" + '\033[0m' print len(list_parametres_stoch_gradient_descence[1]) print ' №6 "   -"' plt.plot(range(len(list_parametres_stoch_gradient_descence[1])), list_parametres_stoch_gradient_descence[1], color='red', lw=2) plt.xlabel('Steps (Iteration)', size=16) plt.ylabel('Sum of squared deviations', size=16) plt.show()

图6“随机梯度下降的偏差平方和（8万步）”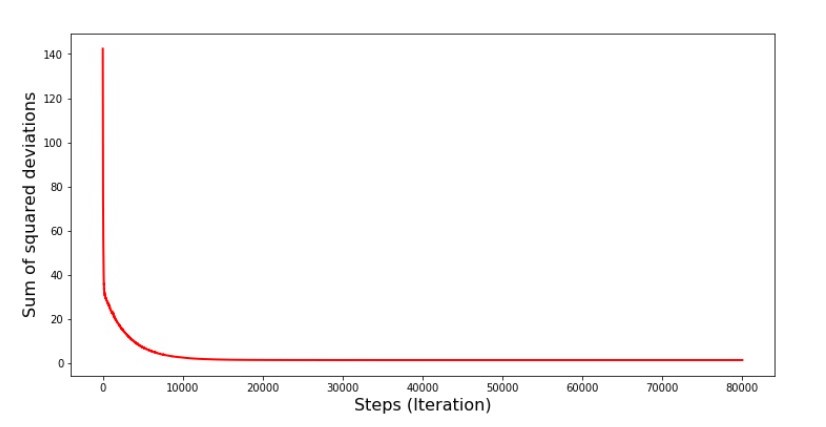

系数的值有所改善，但仍不理想。假设地，可以用这种方式纠正。例如，在最近的1000次迭代中，我们选择产生最小误差的系数值。没错，为此，我们将不得不自己写下系数值。我们不会这样做，而是要注意时间表。看起来很平滑，并且误差似乎均匀减小。实际上并非如此。让我们看一下前1000次迭代，并将其与最后一次进行比较。

SGD图表代码（前1000个步骤）

 print ' №7 "   -.  1000 "' plt.plot(range(len(list_parametres_stoch_gradient_descence[1][:1000])), list_parametres_stoch_gradient_descence[1][:1000], color='red', lw=2) plt.xlabel('Steps (Iteration)', size=16) plt.ylabel('Sum of squared deviations', size=16) plt.show() print ' №7 "   -.  1000 "' plt.plot(range(len(list_parametres_stoch_gradient_descence[1][-1000:])), list_parametres_stoch_gradient_descence[1][-1000:], color='red', lw=2) plt.xlabel('Steps (Iteration)', size=16) plt.ylabel('Sum of squared deviations', size=16) plt.show()

附表7“ SGD偏差的平方和（前1000步）”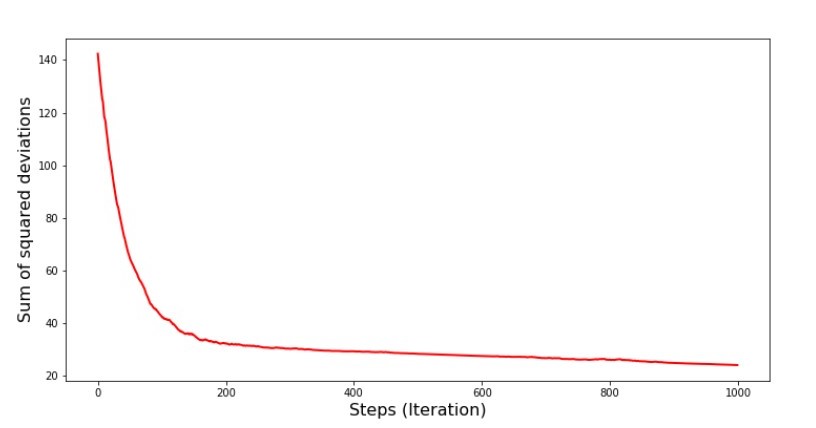

图8“ SGD偏差的平方和（后1000个步）”

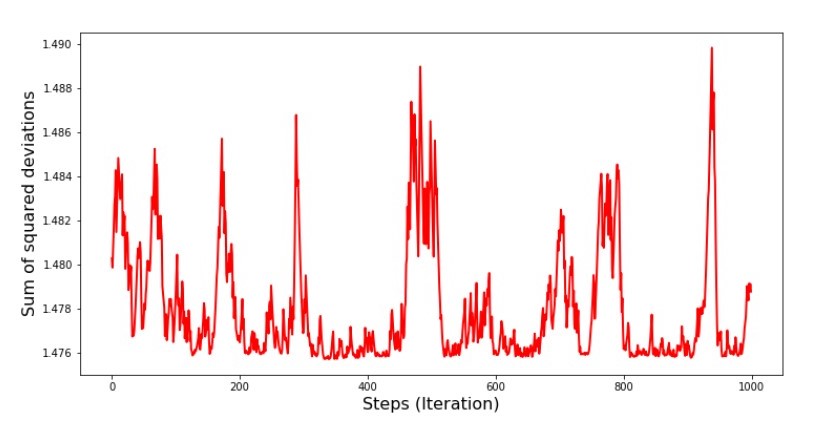在下降开始时，我们观察到误差相当均匀且急剧下降。在最后一次迭代中，我们看到误差在1.475左右变化，在某些点上甚至等于该最佳值，但无论如何它都会上升...同样，我可以写下系数的值

$一$ 和

，然后选择误差最小的那些。但是，我们有一个更严重的问题：我们必须采取8万步（请参见代码）才能使值接近最佳值。这已经与节省计算时间和相对于梯度的随机梯度下降相矛盾。有什么可以纠正和改进的？不难看出，在第一次迭代中，我们自信地下降了，因此，我们应该在第一次迭代中留下很大的一步，并随着前进而减少步伐。我们不会在本文中进行此操作-它已经被拖了。那些愿意的人可以自己思考如何做，这并不困难：)现在，我们将使用NumPy库执行随机梯度下降

$b$ （我们不会偶然发现我们之前确定的石头）

随机梯度下降代码（NumPy）

 #       def stoch_grad_step_numpy(vector_init, X, ind, y, l): x = X[ind] y_pred = np.dot(x,vector_init) err = y_pred - y[ind] grad_a = err grad_b = x[1]*err return vector_init - l*np.array([grad_a, grad_b]) #      def stoch_grad_descent_numpy(X, y, l=0.1, steps = 800): vector_init = np.array([[np.random.randint(X.shape[0])], [np.random.randint(X.shape[0])]]) errors = [] for i in range(steps): ind = np.random.randint(X.shape[0]) new_vector = stoch_grad_step_numpy(vector_init, X, ind, y, l) vector_init = new_vector errors.append(error_square_numpy(vector_init,X,y)) return (vector_init), (errors) #    list_parametres_stoch_gradient_descence = stoch_grad_descent_numpy(x_np, y_np, l=0.001, steps = 80000) print '\033[1m' + '\033[4m' + "  a  b:" + '\033[0m' print 'a =', round(list_parametres_stoch_gradient_descence[0][0],3) print 'b =', round(list_parametres_stoch_gradient_descence[0][1],3) print print '\033[1m' + '\033[4m' + "  :" + '\033[0m' print round(list_parametres_stoch_gradient_descence[1][-1],3) print print '\033[1m' + '\033[4m' + "     :" + '\033[0m' print len(list_parametres_stoch_gradient_descence[1]) print

结果表明，在不使用NumPy的情况下，该值与下降期间的值几乎相同。但是，这是合乎逻辑的。我们将发现随机梯度下降花了我们多少时间。

确定SGD计算时间的代码（八万步）

 print '\033[1m' + '\033[4m' +\ "        NumPy:"\ + '\033[0m' %timeit list_parametres_stoch_gradient_descence = stoch_grad_descent_usual(x_us, y_us, l=0.001, steps = 80000) print '***************************************' print print '\033[1m' + '\033[4m' +\ "        NumPy:"\ + '\033[0m' %timeit list_parametres_stoch_gradient_descence = stoch_grad_descent_numpy(x_np, y_np, l=0.001, steps = 80000)

进入森林越远，云层越深：“自写”公式再次显示出最佳效果。所有这些表明，应该有更多微妙的方法来使用NumPy库，这实际上可以加快计算的速度。在本文中，我们将不会发现它们。您闲暇时会考虑一些事情：)

总结一下

在总结之前，我想回答最有可能来自亲爱的读者的问题。实际上，为什么会有这样的“折磨”与下降，如果我们手中有如此强大而简单的设备，并且以分析解决方案的形式，我们为什么要走上山下（主要是下山）来找到珍贵的低地，为什么要立即将其传送到正确的地方？这个问题的答案在表面上。现在，我们研究了一个非常简单的示例，其中

取决于一个属性

$y_i$

$x_i$ 。在生活中，这种情况并不常见，因此请想象我们有2、30、50或更多的迹象。为每个属性添加成千上万个值。在这种情况下，分析溶液可能无法通过测试并失败。反过来，梯度下降及其变化将缓慢但确实使我们更接近目标-函数的最小值。不用担心速度-我们可能还会分析允许我们设置和调整步长（即速度）的方法。现在实际上是一个简短的摘要。首先，我希望本文中介绍的材料将帮助初学者“约会科学家”了解如何求解简单（且不仅限于）线性回归方程。其次，我们研究了几种求解方程的方法。现在，根据情况，我们可以选择最适合解决问题的解决方案。第三，我们看到了附加设置的功能，即梯度下降的步长。此参数不可忽略。如上所述，为了减少计算成本，应沿下降方向更改步长。第四，在我们的案例中，“自写”功能显示了最佳的时间计算结果。这可能是由于不是最专业地使用NumPy库的功能。但是，尽管如此，结论如下。一方面，有时值得质疑已建立的观点，另一方面，并不总是值得使事情复杂化；相反，有时，更简单的方法来解决问题更有效。并且由于我们的目标是分析三种方法来求解简单线性回归方程，因此使用“自写”函数对我们来说已经足够。

作者的先前工作-“我们使用指数分布研究中心极限定理的陈述”

$\leftarrow$

作者的下一个工作-“我们将线性回归方程式转化为矩阵形式”

$\rightarrow$

文学（或类似的东西）

1.线性回归

http://statistica.ru/theory/osnovy-lineynoy-regressii/

2.最小二乘方法

mathprofi.ru/metod_naimenshih_kvadratov.html

3.导数

www.mathprofi.ru/chastnye_proizvodnye_primery.html

4.梯度

数学/proizvodnaja_po_napravleniju_i_gradient.html

5.梯度下降

habr.com/en/post/471458

habr.com/en/post/307312

artemarakcheev.com//2017-12-31/linear_regression

6. NumPy库

docs.scipy.org/doc/ numpy-1.10.1 /参考/生成/ numpy.linalg.solve.html

docs.scipy.org/doc/numpy-1.10.0/reference/generated/numpy.linalg.pinv.html

pythonworld.ru/numpy/2。 html

求解简单线性回归方程

示例条件

最小二乘法

差异化

下载并格式化数据

可视化

分析溶液

梯度下降

随机梯度下降

总结一下

文学（或类似的东西）

More articles: