我们研究了蒙特卡洛方法 ,今天我们将看到使用旧的具有alpha-beta剪切功能的minimax在2048年如何发挥计算机思维。

本文是在EDISON(一家开发移动应用程序并提供软件测试服务的公司)的支持下撰写的。
用户堆栈溢出发现的解决方案
 ovolve
ovolve ,他在讨论中提到了
如何教AI 2048游戏 。
来自ovolve的评论翻译我是该线程中提到的程序的作者。 您可以查看正在运行的AI或
代码 。
目前,通过在笔记本电脑上的浏览器中执行Java脚本,花费100毫秒的时间来考虑该过程,该程序在大约90%的情况下都可以胜任,尽管效果并不理想,但效果很好。
由于该游戏是一个具有完整信息的离散状态空间,实际上是象棋和跳棋之类的基于回合的游戏,因此我使用了在这些游戏中显示其性能的相同方法,即带有
alpha-beta剪切的 minimax搜索 。 由于这些链接提供了有关此算法的大量信息,因此,我将仅讨论在
静态估计函数中使用的两种主要启发式方法,并在这里对其他人所做的许多直观假设进行形式化。

单调
这种试探法试图确保所有图块值在左/右和上/下都增加或减少。 光是这种启发式方法就反映了许多其他人已经提到的更多猜想,即应该将更多有价值的磁贴分组在一个角落。 通常,这可以防止价值较低的瓷砖积聚,并使板块井井有条,因为较小的瓷砖会层叠成较大的瓷砖。
这是一个完全单调的网格的屏幕截图。 我通过运行带有已安装的eval函数的算法来解决这种情况,以便忽略其他启发式方法,并且仅考虑单调性。

平滑度(平滑度,均匀度)
上述启发式方法本身倾向于创建其中相邻单元的值减小的结构,但是,当然,邻居应该具有相同的含义来组合。 因此,平滑的启发式方法只是测量相邻图块之间的值差,以尽量减少它们的数量。
Hacker News的评论员从图论的角度对该思想进行了
有趣的形式化 。
黑客新闻的形式化翻译昨天我向喜欢图形理论的同事展示了这款游戏,我们还决定考虑如何使用AI解决这款游戏。
最简单的解决方案是minimax,如我所见,它实现得很好。 如果这里的人对minimax不熟悉,OP会编写非常优雅且受好评的代码,这将是一个很好的教程。
我们提出的计算强度较小的方法是以图形G(V,E)的形式模拟游戏状态,其中V是一组活动图块, E是一组连接相邻图块的边,这些图块的权重为c (v1,v2) ,它返回两个图块之间的差的绝对值。 对于每种解决方案,AI都会选择一个使新游戏状态下所有边的权重之和最小的动作。
原因是在游戏中取得进展的唯一方法是让彼此相邻的图块具有相同的值,对于这些图块, G中的权重为0。因此,AI应该尝试使总权重最小。 最后,在板上有大量的相邻边砖,这些边的权重很大,因此AI将尝试将这些砖与其他大砖保持相邻,以最大程度地减少差异。
由于游戏是随机的,因此我描述的方法在最坏的情况下可能不起作用,但它也可以作为树中每个节点的权重函数应用于现有的minimax解决方案。
这是一个完美光滑的网格的屏幕截图,由这个出色的
模拟叉提供 。
(链接到Web存档,而页面上的Java脚本有效,您可以使用键盘向任何方向移动-译者注意)。松散的瓷砖
最后,由于可用空间太少会受到惩罚,因为当比赛场地变得狭窄时,选项可能很快结束。
仅此而已! 在优化这些条件的同时搜索游戏空间会产生令人惊讶的良好性能。 使用这种通用方法而不是显式编码的移动策略的好处之一是该算法通常可以找到有趣且出乎意料的解决方案。 如果您观察他的进步,他通常会做出惊人而有效的动作,例如墙壁或角落的突然变化,在此附近他可以建立自己的游戏。

零钱
屏幕截图展示了这种方法的强大功能。 我取消了图块限制(以便它们在达到2048后继续增长),这是八次测试后的最佳结果。
是的,这是4096和2048。=)这意味着他已经在一块板上达到了难以捉摸的2048磁贴。
本文下面给出了带有alpha-beta剪切和来自stackoverflow用户的静态评估功能的minimax的Java脚本代码。
minimax方法专用于一些优秀的habr文章,因此我们省略了对其组成的学术详细解释。 对于那些
加入IT社区的人来说,我最近听到了漂亮的术语“ minimax”和“ alpha-beta裁剪”,但不知道这意味着什么,让我们尝试在几个段落中按字面意思解释最笼统的含义。
极小值
在某些游戏中,两个玩家(依次行动)之间的游戏过程可以表示为所谓的选择树。 在每个特定位置,每个玩家通常在其移动的不同选项之间进行选择。 并且,针对这些选项中的每一个,对手也可以在许多方面像对手。
选项树的片段由于在游戏的任何时刻,都有有关比赛场地状态的完整信息,因此始终可以准确估算位置的当前状态。 这种功能称为
静态评估功能或缩写
SFO 。 而且,此功能在评估特定位置时越重要,一个玩家的位置就越有利(我们称其为
最大化玩家 )。 评估位置时此函数的数值越小,第二个玩家的位置就越有利(我们称其为“
最小化玩家” )。
每次移动后,位置都会改变,因此其得分也会改变。 考虑选项树时,每个玩家不仅需要选择评分最适合他的那些分支。 您还应该避免那些位置评价对对手有利的分支。
假定对手也受到理性主义的引导,并且避免了可能导致他失败的选择。 就是说,每个玩家在选择一个选项时,都会从最大化自己的利益而同时最小化对手的利润中获得收益。
这是极小值。
Alpha Beta裁剪
显而易见:从给定位置计算树到更大深度的人,他有更多获胜的机会。 但是有一个麻烦:游戏中的选择树有一个令人讨厌的习惯,即在每个嵌套级别上分支并呈指数增长。 程序的计数能力,甚至更多的人受到限制,计数“恰到好处”远非总是可能。 可以很容易地证明,玩家已经计数到一个可以对比赛场地进行良好评估的位置,但是从字面上看,在下一级别(不可读)上,对手有机会做出这样的举动,从而将位置估计值从根本上改变为相反方向。
谁该怪谁该怎么办? 复杂的树遍历应归咎于计算复杂性;建议通过切断不必要的分支来解决。 如果评估位置的玩家看到选项树的某个分支:
或比已经分析过的其他分支机构少赚钱,
或比已经分析过的其他分支机构更有利于对手,
玩家就放弃了这个分支,不浪费时间和资源去考虑这个明显更差的分支的子选项。
这使您可以分配更多计算资源,以便在选项树中分配更大的渲染深度来计算更有利的分支。 在评估选项树不同级别上的公平竞争环境的过程中,玩家使用两个动态变化的系数进行操作
-alpha (分支中最少遇到的SFD值-即更有利于最小化玩家)和
beta (分支中最多遇到的SFO值-更有利于玩家最大化)。 在每个级别上,将当前位置的SFD与
alpha和
beta系数进行比较,就可以扫描(而不是完全计算出它们)
不利于评估位置和/或
对对手
更有利的玩家的分支。
这是alpha beta裁剪。
具有alpha beta裁剪的递归minimax函数
带有AI的2048是作为带有VBA宏的Excel应用程序实现的,这就是带有alpha beta剪切的minimax算法如何看起来像卑鄙的视觉基础。 用Java脚本编写Ovolve代码 function AI(grid) { this.grid = grid; }
静态评估功能
由于在选项树的每个级别上您都必须评估比赛环境(为了确定对哪个球员而言,估计的位置实际上更有利),因此您需要确定哪种标准将好位置与坏位置区分开。
我们假设最大化玩家是决定要移动所有图块的4个方向(上,左,右,下)中的哪个(或AI)的人。 一个最小化的参与者是在最不合适的地方随机生成2或4的那个阴险的子例程。
SFO是从最大化参与者的角度进行编译的。 比赛场地的SFD评分越高,“极简主义者”的位置就越好。 越低-“极简主义者”在董事会上的职位越愉快。
在2048的情况下-移动瓷砖的人认为哪些因素有利?
单调
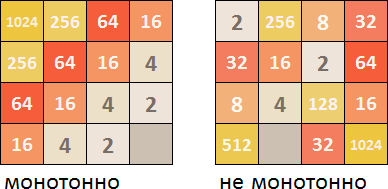
首先,期望在一些方向上以升/降顺序布置瓦片。 如果不这样做,那么当生成新的图块时,运动场将很快被不同大小的随机排列的图块阻塞,这些图块无法立即正常地相互连接。
在西伯利亚联邦区,您需要在所有四个方向上(从上至下,从左至右,从右至左,自下而上)进行查看,并计算图块在哪里递减或递增。 如果在进行中存在不适合一般序列的图块,则这会降低单调的数值系数。 然后,从所有方向的4个系数中,选择最佳的一个,并考虑到西伯利亚联邦区的总价值。
光滑度

此外,更理想的是,从排成一排的瓷砖开始的进度不仅增加,而且不减少(或者最好减少而不是减少排的数量,而不是不增加),也就是说,当同一块瓷砖在附近时,允许它们塌陷成一个块,获得点数并增加增加运动场上的可用空间。
因此,西伯利亚联邦区正在运动场上寻找相同的相邻砖块,并以特殊系数考虑了此类对的数量。
空单元格

显然,自由空间越多,机动性就越大,快速失去的可能性就越小。
SFO会考虑场地上的空单元,而其中的空单元越多,该位置对于最大化玩家来说就越有利可图。
最大瓦数
由于此游戏的主要目的是在场地上获得较大的磁贴,所以越好-2048、4096、8192(或您有实力和耐心的任何东西),因此应将最大磁贴值越大的选项视为最赚钱的SFD。
西伯利亚联邦区2048
用Java脚本编写Ovolve代码 function Grid(size) { this.size = size; this.startTiles = 2; this.cells = []; this.build(); this.playerTurn = true; }
2048.xlsm
Excel应用程序本身
可以从Google下载 。
在上一篇文章中描述了该应用程序的功能
,其中AI使用Monte Carlo方法播放 。 今天的解决方案已添加到现有的蒙特卡洛中。
AI和2048系列的所有文章
- 蒙特卡洛
- Minimax + Alpha Beta裁剪
- 等待最大
- 神经网络