TextRadar模糊搜索算法-基本方法

TextRadar模糊搜索算法-基本方法

与模糊字符串比较不同，当两个比较字符串相等时，在模糊搜索任务中突出显示搜索字符串和数据字符串，因此有必要确定两个字符串之间的相似度，而不是两个字符串的相似度。

问题陈述

数据字符串和搜索字符串是由单词组成的任意字符集-由空格分隔的字符组。

需要在数据行中通过字符的组成和相对位置找到最接近搜索行的片段集。

为了评估搜索结果的质量，请计算相关系数，其相关系数的值应在0到1的范围内，其中0对应于数据字符串中搜索字符串完全不存在字符，而1则对应于数据字符串中搜索字符串以不失真形式存在。

搜索应通过对源代码行进行逐字符分析，同时考虑到行中字符和单词的相互排列，但不应考虑语言的语法和词法。

算法说明

搜索分几个阶段进行。

巧合矩阵的构造

匹配矩阵（M）是二维矩阵，其列数对应于数据字符串的长度，行数对应于搜索字符串的长度。 符合矩阵的元素取值0或1取决于行的相应字符是否符合（空格（单词定界符）除外）。
数据字符串“ ABCD EF”和搜索字符串“ ABC”的匹配矩阵具有以下形式：



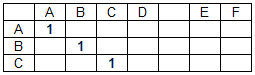
如果d（i）= s（j），则匹配矩阵元素m（i，j）= 1，其中D是数据字符串字符数组，S是搜索字符串字符数组，i是匹配矩阵M的列号M（数据字符串的字符号） ），j是匹配矩阵的行号（搜索字符串中字符的编号）。 在其他情况下，m（i，j）=0。不考虑单词分隔符（在我们的情况下为空格）的匹配，即：如果d（i）= s（j）=，则m（i，j）= 0 。

匹配矩阵对角线

重合矩阵M的元素形成对角线。 如果矩阵的元素的索引i和j同时相差+1或-1，则它们在同一对角线上。



对角线对应于搜索字符串在沿数据字符串的偏移序列中的位置。



上图中对角线之一的元素和相应的偏移以蓝色突出显示。

在模糊搜索问题中使用相对于彼此的一系列线位移的想法可以追溯到用于在干扰背景下检测雷达信号的众所周知的技术，该技术涉及无线电信号互相关函数的计算。 互相关函数确定两个不同信号v（t）和u（t）的副本的相似度，相对于彼此偏移时间τ，并定义为积分：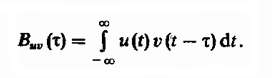



对角线总数由以下公式计算：



对角线的长度等于搜索字符串的长度。

比赛组

在重合矩阵的对角线上连续跟随的单位形成匹配组。 以下是数据字符串“ ABCD DEF JH”和搜索字符串“ ABC DE J”的匹配组-位于不同对角线上的4个组。

投影矩阵

匹配矩阵的对角线和其中包含的匹配组映射到搜索字符串和数据字符串的相应部分，分别形成两个投影矩阵-搜索字符串和数据字符串。 对于我们的示例，投影矩阵如下所示：



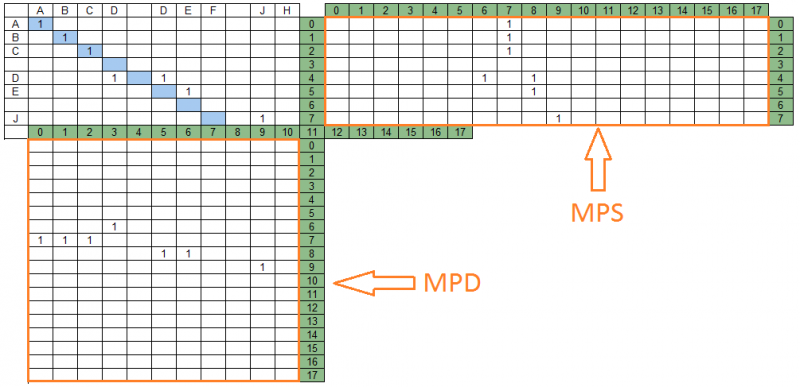
在上图中，匹配矩阵的右侧是在搜索字符串上的投影矩阵-MPS，在下面-是在MPD数据字符串上的投影矩阵。 MPS列的数量等于MPD行的数量，并且等于匹配矩阵的对角线数量-在我们的示例中，为18。

搜索一组结果

为了解决该问题，有必要找到这样的一组组，即它们最大程度地“覆盖”了搜索字符串，且碎片最少（尽可能大），并且投影矩阵中没有相互交集，并且它们到数据字符串的映射将最接近“原始”搜索字符串。 。

投影矩阵中的组的交集

在我们的示例中，MPS矩阵中有相交的组-在下图中，它们以红色突出显示。 此外，在MPD矩阵中，这些相同的组不相交，在图中以绿色突出显示。



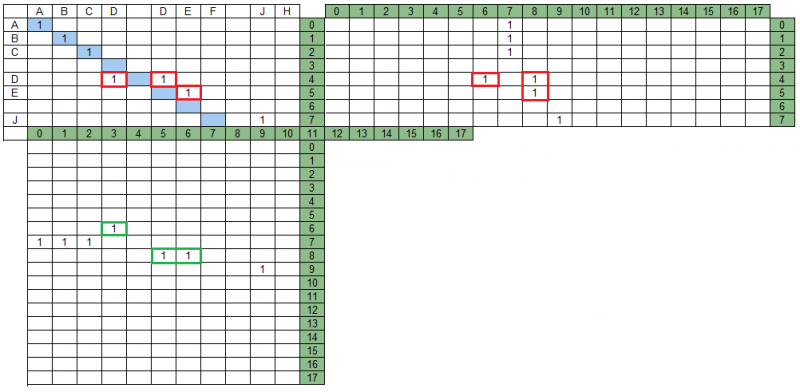
对组的结果集的搜索意味着并非所有组都将包括在其中，并且在分析投影中的组的相互交集时可以修改（截断）其余的一些组。

可以通过遍历所有组表的“无限”循环（循环的迭代数不超过组数）来搜索结果集，首先将匹配矩阵的组放入其中，并在每次迭代时执行以下操作：

1. 根据某些参数（取决于要解决的问题的上下文）选择最佳的参数-在最简单的情况下，这可能是遇到的最大尺寸的第一组参数的选择；
2. 将最好的组放置在结果组表中，并将其从所有组的表中删除（已爬网的行）；
3. 从与组投影矩阵中选定的最佳组相交的组表中删除（或截断）。

下图显示了本示例的最佳组组-组组以橙色突出显示。



在相交处理期间删除的组（在MPS矩阵中与第二次迭代的最佳组相交）以红色突出显示。

数据行中的搜索结果将如下所示：

相关系数的计算

为了量化搜索结果，将找到的组的长度与搜索字符串的单词长度进行比较（组组成评估），并将搜索字符串的总长度与数据字符串中找到的组的长度进行比较。 假设评估所发现组的组成的重要性高于数据行中范围估计的重要性，这在计算相关系数的公式的加权系数中已得到考虑：



其中组组成系数计算为找到的组的平方长度的总和与搜索字符串中单词的平方长度的总和之比：



长度因子是搜索字符串的长度与数据字符串上找到的组的总长度之比。 如果以此方式获得的值大于1，则取其反值：



对于我们的示例：

估计计算范围

最耗费资源的操作是：

• 确定匹配矩阵M-将矩阵元素的数量定义为搜索字符串的长度与数据字符串的长度的乘积：
• 在数据和搜索字符串上定义投影矩阵-矩阵元素的数量用于MPS：（L+L-1）*L，用于MPD：（L+L-1）*；
• 所有组表的形成-组数将不超过值L*L/ 2;
• 搜索结果的组集合-循环的迭代次数不超过组的初始数目，即L*L/ 2。

因此，计算总量将是搜索字符串的长度乘以数据字符串的长度的乘积：



计算量相对于源数据大小的线性是一个重要的论点，有利于算法的实际应用。

非线性度

值得注意的是，线性是由于简化了查找结果组集的过程。 在一般情况下，如果我们考虑将所有组放置在数据行上的所有可能选项，并考虑可能的相交处理选项，并从可能的组中选择最佳的组 ，而不是在循环的每次迭代中选择一个组 ，则计算量将相对于大小不再线性源数据。 计算量对源数据大小的非线性依赖性极大地限制了实际应用的可能性。

找到余额

为了确保搜索质量和对资源的需求之间达到最佳平衡，重要的是为所得的组选择正确的搜索方法，通常，这可以使用要解决的问题的上下文特征来完成。

已在textradar.ru网站上部署了演示台，您可以在其中测试算法的操作。

与类似物的比较：TextRadar模糊搜索算法与类似物的比较：Lucene，Sphinx，Yandex，1C