在对复杂形状的对象进行建模时， 圆角化是计算机辅助设计系统中最困难的任务之一。 对于圆角的构造以及CAD中的所有几何图形，几何图形核心负责。

从内核开发人员的角度来看，由于它们的无限多样性，不可能涵盖所有取整选项。 我们的数学家一直在向C3D核心添加新的特殊情况，并且最近对三张面孔进行了四舍五入（或完全四舍五入）。

C3D Labs的数学家兼程序员Anna Ladilova说，它的复杂性以及算法的工作原理。

什么是四舍五入？

假设我们有一个包含三个面链的主体-中央（上）和侧面（右和左）。 需要用圆角表面替换中心面，该圆角表面应能平滑地插入相邻的侧面。 这个新的表面将是完整的四舍五入。 通常，它具有自动检测到的可变半径。



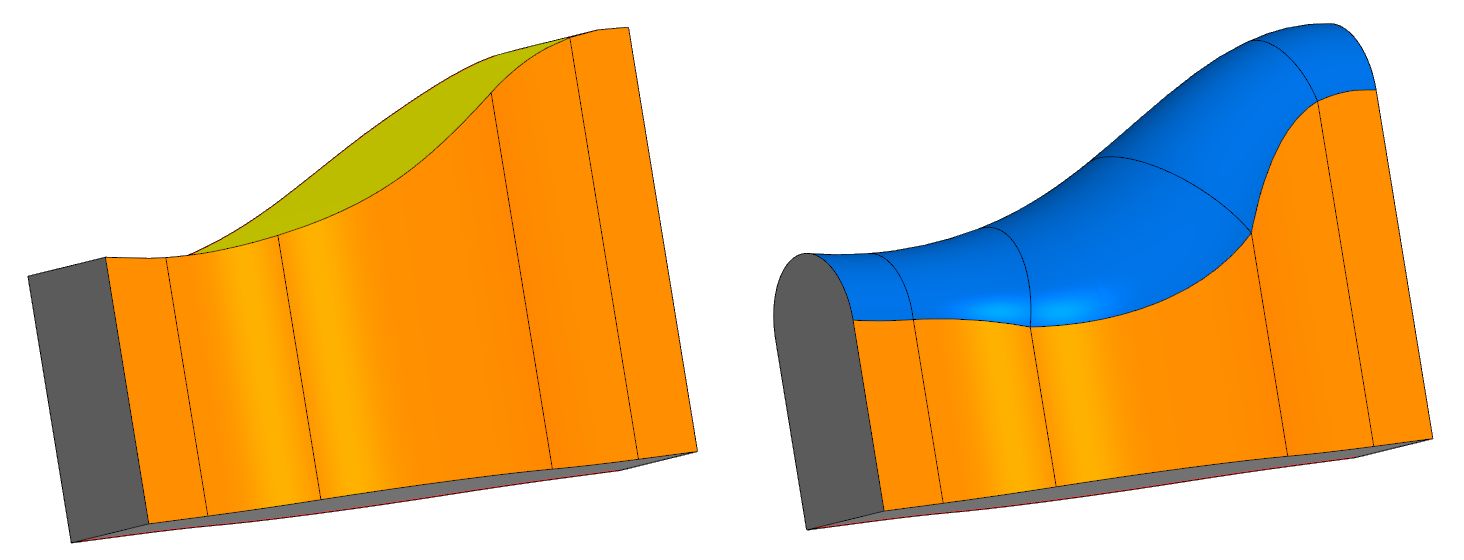
在许多众所周知的CAD系统中，都执行了全圆角操作，但是没有公开其数学运算。


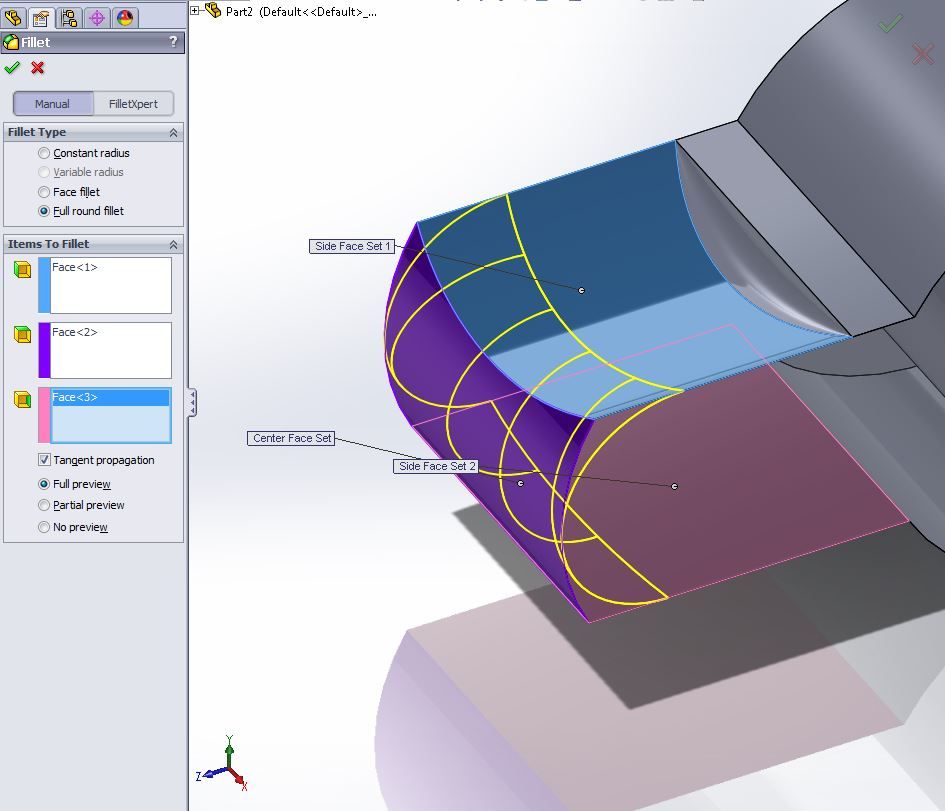Solidworks全圆角加工

因此，我们开发了自己的算法。 而且它与其他开发人员的算法不同。

操作虽然被称为相同，但导致的结果略有不同。 这表明SolidWorks为三面倒圆给出了不同的定义。


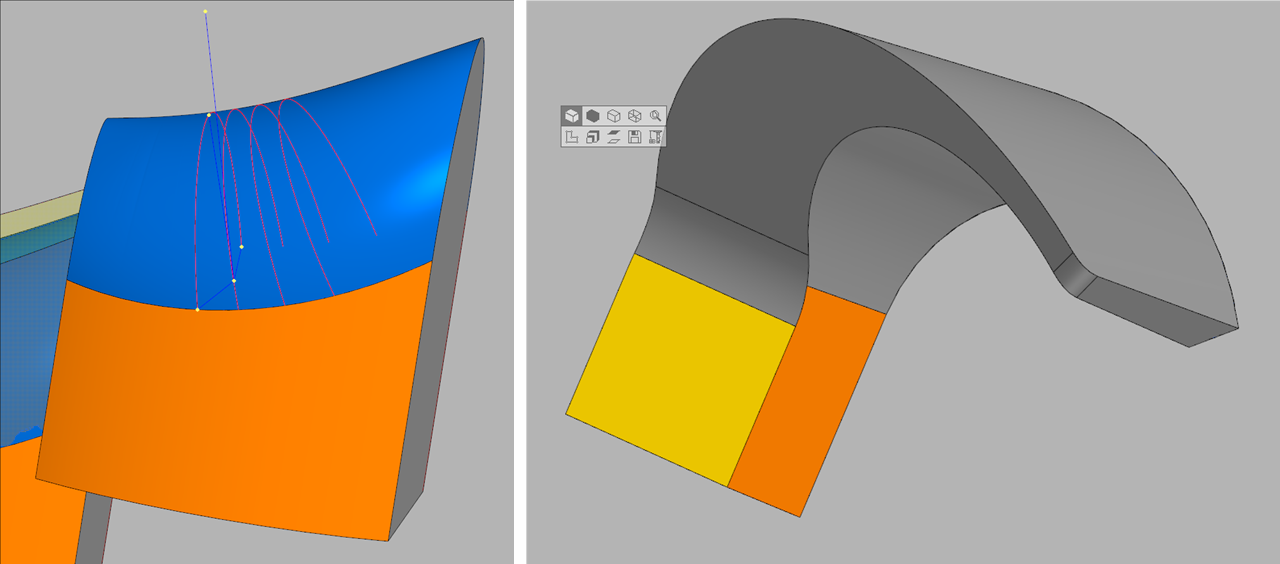
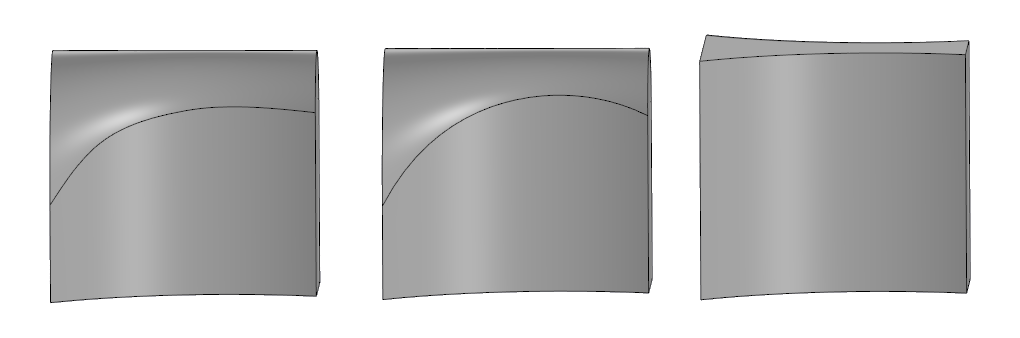右边是原始模型，中间是SolidWorks中的完整取整，左边是C3D。

全舍入算法

构造任何类型的圆角的任务包括以下几个阶段：

1. 将给定的链分解为基本成分（要对三个面四舍五入，正好是三个面：左，右和中心）。
2. 始终安排基本组件。
3. 为每个基本组件构建一个圆角曲面。
4. 用肋缝缝制相邻的圆角表面。
5. 要处理圆角链的端部，即正确地将它们连接到修改后的主体。

此过程的关键是第三步：为三个给定的面构建圆角曲面。

为了构造所需的表面，首先必须确定圆角接触三个面中每个面的曲线。 在一般情况下，这些曲线只能构造为穿过预先计算的已知点的样条曲线。

考虑如何计算三重点-每个样条线一个。


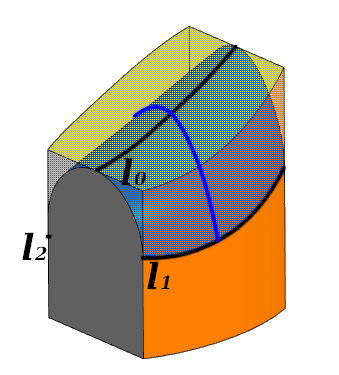元素处理。 圆角沿曲线l ₀接触三个面中的每一个； _{1 2} 。 蓝线显示横截面

在每个横截面中 $$$ABC$：

• $$$OA = OB = OC$-自动计算
• $$$OA，OB，OC$垂直于相应点处的曲面的切平面
• $$$p$_0-锚点，位于平面中 $$$ABC$。

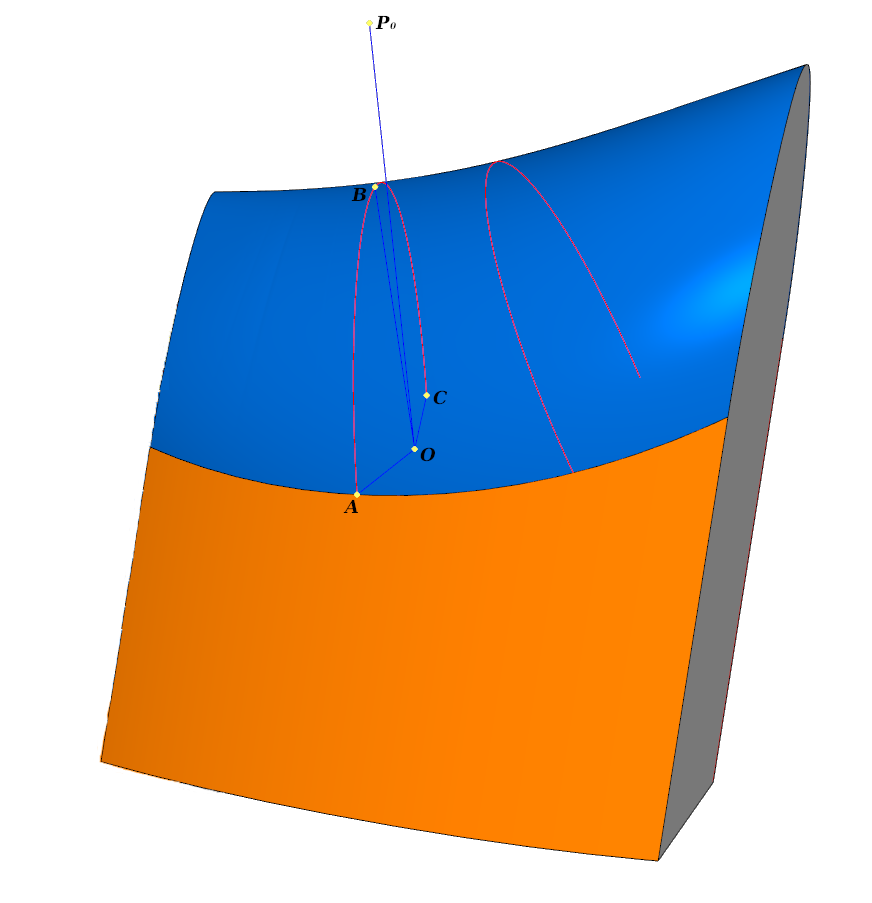
我们通过一定定义范围内的半径矢量定义中心，左侧和右侧面的初始表面。 让侧面由半径向量定义 $$_1个 $$$（u，v）$和 $$₂ $$$（z，w）$和中央一 $$₀ $$$（x，y）$。 我们引入一个正数值参数 $$$d$。

表示为 $$$n$₀ $$$（x，y）$， $$$n$_1个 $$$（u，v）$， $$$n$₂ $$$（z，w）$指向相应表面的单个法线，指向“向内”。


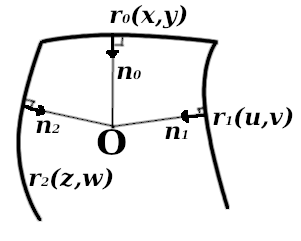制作圆角时的横断面

我们要求这些法线的末端伸入 $$$d$次，命中一分 $$$O$。

在微分几何方面，我们的要求可以由具有七个参数的七个方程式的系统来表述：

$$$dn$₀ $$$（x，y）$= $$$dn$_1个 $$$（u，v）$，
$$$dn$₀ $$$（x，y）$= $$$dn$₂ $$$（z，w）$，
（ $$₀ $$$（x，y）$-- $$$p$₀ $$_1个 $$$（u，v）$-- $$$p$₀ $$₂ $$$（z，w）$-- $$$p$₀ ）= $$$0$，

在哪里

• $$$d$-可变半径
• $$$p$_0-锚点
• $$$x，y，u，v，z，w$-来自参数定义区域的变量。

使用数值方法的算法（例如，牛顿法），我们找到了该系统的解决方案： $$$x$₀ $$$y$₀ $$$u$₀ $$$v$₀ $$$z$₀ $$$w$₀ $$$d$₀ 。

该解决方案使用表面定义了接触点：

• $$₀ （ $$$x$₀ $$$y$₀ ）
• $$₁ （ $$$u$₀ $$$v$₀ ）
• $$₂ （ $$$z$₀ $$$w$₀ ）

以及半径 $$$d$₀ 。

通过一系列要点 $$$p$₀ ，我们得到带有曲面的切线三元组，从中可以恢复“接触曲线” $$$l$₀ $$$l$_1个 $$$l$_2，因为Hermite样条线穿过计算的点。

范围[ $$$t$_分钟， $$$t$_max ]所有曲线都相同，参数 $$$t$_我对应一个点 $$_0i $$_1i $$_2i 。 此外，这些曲线用于计算所需的圆角横截面。

我们修复了一些参数 $$$t$并为其计算积分：

• $$₀ $$$（x（t），y（t）），$
• $$_1个 $$$（u（t），v（t）），$
• $$₂ $$$（z（t），w（t））$。

我们构造一条通过这些点和正交于它们的法线向量的样条曲线 $$$n$₀ $$$（x（t），y（t））$， $$$n$_1个 $$$（u（t），v（t））$， $$$n$₂ $$$（z（t），w（t））$相应地。

如果问题陈述稍有变化，并在给定点处搜索曲线，并在这些点处搜索切线向量，那么可以在例如Nikolai Golovanov的《几何模型》一书中找到实现样条曲线的方法。

该书详细描述了使身体边缘变圆的方法，特别是表明，变圆的横截面可以实现为由三个点定义的NURBS曲线。 如果将三个面倒圆，则将由五个点确定类似的曲线。

因此，对于每个参数 $$$t$我们可以定义一组用于构造NURBS的点，因此可以定义圆角曲面横截面的每个点。 因此，完全解决了表面构造的问题。

在算法这一部分的描述中，还有一个小问题-如何“选择”一组要点 $$$p$₀对应于横截面，通过该横截面可以轻松恢复“触摸曲线” $$$l$₀ $$$l$_1个 $$$l$₂ ？

采取一些预先选择的曲线似乎很合理。 我们将不讨论构建此曲线的细节；我们仅注意它应该是平滑的，没有自相交，并且“平均”限制左右中心面的边链。


左，横截面，点相关 $$$p$₀ 。
在右侧，图形可能非常复杂，因此正确选择“辅助”曲线是一项单独的任务。

现在，我们能够为最简单的基本情况构建圆角曲面，我们可以继续处理一个更复杂的问题：为一连串的面构建曲面。
这里的主要问题是以平滑的方式“缝制”相邻的表面。 这是算法的第四步。

困难恰恰在于交联的平滑度，因为表面是用不同的初始数据构建的。 为了确保平滑，必须采取各种技巧：在距边界一定距离的位置上更改纵向矢量的方向和长度，在边界上更改权重函数的导数的值，等等。 结果在图中可见：更平滑的斑马线对应于更平滑的表面。




上面是没有平滑算法的模型。 下面-应用算法后。

总结

作为我们研究的结果，C3D几何核能够构造圆角横截面，支撑曲线和三个面的圆角； 知道如何通过选择参数化来平滑表面； 部分了解如何平滑地接合相邻的圆角曲面。


作者-Anna Ladilova博士，数学家/程序员C3D Labs