椭圆曲线加密在TLS 1.3中的工作方式

读者警告：

为了（某种程度上）简化描述过程并收紧我们将要写的文章的数量，有必要做一个重要的评论并立即陈述主要限制条件-我们今天将在实用上告诉您的一切问题的一面仅在TLS 1.3方面才可行。 这意味着，尽管您希望ECDSA证书可以工作，但仍可以在TLS 1.2中使用，但可以提供向后兼容性，但实际握手过程，密码和客户端-服务器基准测试的说明仅涵盖TLS 1.3。 当然，这与现代加密系统背后的算法的数学描述无关。

这篇文章既不是由数学家也不是由工程师撰写的，尽管他们帮助找到了解决可怕数学问题的方法，并对此进行了评论。 非常感谢Qrator Labs的员工。

（椭圆曲线）Diffie- Hellman（短暂）

Diffie – Hellman在21世纪的传承

当然，这不是从Diffie还是Hellman开始的。 但是，为了提供正确的时间表，我们需要指出主要日期和事件。

现代密码学的发展有几个主要角色。 最值得注意的是，艾伦·图灵（Alan Turing）和克劳德·香农（Claud Shannon）都在计算理论，信息理论以及一般密码分析领域进行了大量工作，迪菲（Diffie）和海尔曼（Hellman）都因提出了公共密钥的想法而被正式认可。 （或所谓的非对称）加密技术（尽管众所周知，在英国，加密技术已经取得了重大进展，并且长期处于保密状态），这使这两位先生成为了先驱。

到底是什么？

好吧，这听起来很奇怪。 但是，在1976年11月6日之前，还没有公众对公用密钥加密系统的了解。 惠特菲尔德·迪菲（Whitfield Diffie）和马丁·海尔曼（Martin Hellman）（实际上是拉尔夫·默克尔（Ralph Merkle））-数学家，计算机工程师和发烧友以及密码学家是第一批。

对于那些不知道的人-由于二战中密码分析的作用及其对保密信息的巨大影响，这两个认为自己拥有最先进的密码学知识的国家-美国和英国将加密纳入了弹药清单并加以利用严格的出口禁令（同时削弱了针对家庭私人和商业用途的加密实施）。 为此，直到1997年英国政府研究人员在政府通信总部的非对称密钥交换技术上工作并开发类似方案的英国研究人员直到1997年才意识到这项发明，当时对密码算法的限制及其描述无效。

回到我们的双重发明家-Diffie和Hellman特别革新了什么？

让我们看一下他们的原始论文，完美地说明了他们所引入的巨大飞跃（甚至在理论上与他们的研究论文一起）：

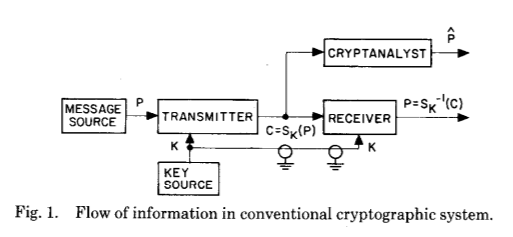
和以下之一：

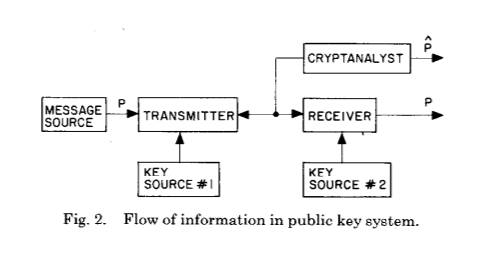
这两幅图完美地说明了在加密和密码分析几个世纪以来，惠特菲尔德·迪菲（Whitfield Diffie）和马丁·赫尔曼（Martin Hellman）所进行的巨大变革-密码计算的结果是建立了共享的秘密密钥。

让我们看一下另一种颜色不错的图片：



它解释了发生了什么。 在Diffie和Hellman密钥协商发明之前，只有一个对称密钥-它既用于加密也用于解密消息。 如果要给某人这样的“密钥”，则必须通过“安全”通道进行转移。 您可以立即想象出这种上一代方案的所有限制-您需要一个已经建立的安全通道， 不能重用密钥 ，并且理想情况下，密钥的长度应与消息的长度相同。

克劳德·香农（Claude Shannon）在其战时分类的著作“ 保密系统的传播理论 ”中证明，所有理论上坚不可摧的密码都必须具有与一次性密码簿相同的要求，即著名的Vernam密码，即对称多字母流密码的作者。

再次，我们将看一下原始论文：


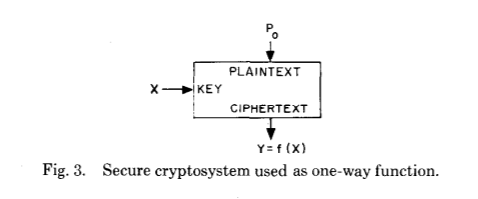
在进一步探讨之前，让我们问问自己-在具有如此悠久历史的应用领域，尤其是在战争时期，两个人如何取得了如此巨大的进步？
好吧，因为：

• 信息理论 ，由克劳德·香农（Claude Shannon）提出；
• 计算理论最受Alonzo Church，John von Neumann和Alan Turing的影响；
• 而且，更重要的是， 可计算性理论主要基于图灵的工作，我们可以说所有这些理论都是在20世纪同一时期发展和成熟的。 Diffie和Hellman都提到克劳德·香农（Claude Shannon）是他们工作中最重要的影响者。

Lenstra的“ 通用安全性 ”说明了“破坏”具有各种密钥长度的对称密码系统所需的能量。 事实证明，打破228位长的椭圆曲线键将需要与煮沸地球上所有水所需的能量相同的能量。 但是，仅在考虑已知算法和硬件的情况下它才有效，因为严格来说，没有人知道是否存在效率更高的算法或硬件。 228位EC密钥可与2380位长的RSA密钥相提并论。 尽管在此估计中，RSA和EC密钥都用于非对称加密方案中，但此类密钥的长度在某种程度上等效于128位对称加密密钥。

不难想象，“难以计算”的东西将需要大量的能量和/或时间来进行计算。 我们倾向于认为计算机可以“计算一切”，但事实证明事实并非如此。 首先，存在一些不确定的例子，例如停止问题，尽管在密码学领域，我们可以避免这种陷阱。 其次，如果我们考虑运行特定算法所需的时间，则它可能是任意高的。 这就是我们在密码学中所利用的。 计算运行相应算法所需的时间是否像多项式一样取决于输入大小（以位为单位），是一个“容易”计算的问题：$$ $内联$ T（n）= O（n ^ k）$内联$ ，对于一些正常数$$ $内联$ k $内联$ 。 在计算复杂度理论领域，此类问题形成了P复杂度类 。

P复杂度类别几乎是核心问题，因为它表示存在确定性多项式时间算法的问题。 另一个复杂性类别是NP （难于计算的问题），代表一组决策问题，即需要“是”或“否”答案的问题，这些问题可以在多项式时间内得到验证。 您在这里看到“证明”一词吗？ 那就是我们进入陷门功能的地方，属于NP复杂度类。


积分： xkcd

单向功能； 活板门功能

根据定义，单向函数就是这样一种函数，它易于在每个输入上进行计算，但难以逆转，即仅计算给定输出的原始输入。 “简单”和“困难”是指上面的计算复杂性理论定义。 有趣的是，单向函数的存在没有得到（数学上的）证明，因为它们的存在将证明P和NP复杂度类不相等，而如今P等于NP或不等于NP都是一个未解决的问题。 因此，请记住，所有现代加密技术都依赖于未经证实的假设。

现在，Diffie和Hellman在他们的原始论文中介绍了另一种称为“活板门功能”的单向功能。 它们有何不同？
正如他们在具有里程碑意义的论文中解释的那样：

在公共密钥密码系统中，加密和解密由不同的密钥E和D控制，因此从E计算D在计算上是不可行的（例如，要求$$ $ inline $ 10 ^ {100} $ inline $ 说明）。 可以在不破坏解密密钥D的情况下[在目录中]公开加密密钥E。这使系统的任何用户都可以将消息发送给任何其他已加密的用户，使得只有目标接收者才能解密该消息。 ..与密钥分发问题相比，认证问题可能是普遍采用电信进行业务交易的更为严重的障碍……它是任何涉及合同和计费系统的核心。

按照惯例，通常使用密码字符“ Alice”和“ Bob”（寻求安全通信）来解释公钥概念。 爱丽丝和鲍勃同意大整数$$ $内联$ n $内联$ 和$$ $内联$ g $内联$ 与$$ $内联$ 1 <g <n $内联$ 。 选择会影响系统的安全性。 “模数$$ $内联$ n $内联$ 应该是素数 更重要的是$$ $ inline $（n-1）/ 2 $ inline $ 还应该是主要的<...>并且$$ $内联$ g $内联$ 应该是原始的根模$$ $内联$ n $内联$ <...> [和]$$ $内联$ n $内联$ 应该至少为512位。” Diffie – Hellman协议可以用5个步骤以元素形式表示。

1. 爱丽丝选择$$ $内联$ x $内联$ （一个大的随机整数）并计算$$ $内联$ X = g ^ x \ bmod n $内联$
2. 鲍勃选择$$ $内联$ y $内联$ （一个大的随机整数）并计算$$ $内联$ Y = g ^ y \ bmod n $内联$
3. 爱丽丝发送$$ $内联$ X $内联$ 给Bob，而Bob发送$$ $内联$ Y $内联$ 给爱丽丝（他们保留$$ $内联$ x $内联$ 和$$ $内联$ y $内联$ 彼此的秘密）
4. 爱丽丝计算$$ $内联$ k = Y ^ x \ bmod n $内联$
5. 鲍勃计算$$ $内联$ k'= X ^ y \ bmod n $内联$

结果，爱丽丝和鲍勃的价值相同$$ $ inline $ k = k'$ inline $ 作为一个共享的秘密。

活板门功能是一种单向功能，如果有一条称为“活板门”的特殊信息，则可以查找其倒数。 听起来很容易，尽管很难找到这样的功能-第一种可行的方法是在实现了以其创建者Ron Rivest，Adi Shamir和Leonard Adleman命名的RSA公开密钥加密非对称加密算法的过程中找到的。

RSA

在RSA中，函数求逆的难点是基于以下事实：因式分解（找到一个数的质数乘方）比乘法需要更多的时间，或者在这里我们应该说，在经典计算机上没有用于分解大整数的多项式时间方法具有但是，尚未证明不存在。

像其他任何公共密钥加密系统一样，在RSA中，有两个密钥：公共和私有。 RSA接受输入消息（表示为位字符串），然后对其应用数学运算（对大整数取模），从而获得与随机变量难以区分的结果。 解密将获得此结果，并应用类似的操作以取回原始消息。 在非对称密码学中，加密是使用公钥进行的，而解密则是使用私钥进行的。

怎么了 因为操作数属于有限循环组（在模块化算术中一组带有乘法的整数）。 omputers不能很好地处理任意大数，但是，幸运的是，我们的整数循环组执行的操作称为“环绕”-大于允许的最大值的数字会被包裹为一个有效范围内的数字。 这使我们可以使用“不超过”长度的键进行操作。 在椭圆曲线密码学中，也使用循环（乘法）组，但结构稍有不同，我们将在后面看到。

基本上，RSA的工作是取两个大质数并将它们相乘以获得所谓的模数。 所有其他要处理的数字都位于零和模数之间。 模数将成为公共密钥的一部分，其位长决定密钥的长度。 公用密钥的第二部分是在零和Euler的模数（现代RSA实现采用Carmichael的模数而不是Euler的模数）之间选择的数字，并带有一些其他限制。 最后，通过解决一些模块化方程来计算私钥。 要加密数字，我们只需将其提高到等于公钥的幂，然后将数字解密回来，我们将其提高到等于私钥的幂。 由于该组具有周期性，因此我们可以得到初始编号。

如今，RSA存在两个重大问题，一个是另一个问题的结果。 随着密钥的长度（即，其位数）的增加，复杂度因子的增长并不像人们期望的那样快。 那是因为存在次指数（但仍然是超多项式 ）分解算法 。 因此，为了保持适当的安全级别，RSA密钥的长度需要比ECC密钥的长度更快地增长。 这就是为什么当今最广泛使用的RSA密钥的长度为2048或3072位。

稍后，我们将通过比较用Let's Encrypt授权签名的RSA和ECDSA证书，从数字上看到密钥的长度如何影响整体密码系统的效率。

（椭圆曲线）数字原位算法

对更好的活板门功能的探索最终导致密码学家在80年代中期致力于椭圆曲线的数学领域积极发展。

在一篇文章中描述椭圆曲线密码学将是最终的任务，因此我们不会。 相反，让我们看一下基于离散对数问题的椭圆曲线活板门函数。

椭圆曲线密码学有许多入门和更深入的介绍，如果您对数学感兴趣，我们特别推荐Andrea Corbellini的“ ECC：温和介绍” 。

我们感兴趣的是相当“简单”的参数。

椭圆曲线由以下等式定义：$$ $内联$ y ^ 2 = x ^ 3 +轴+ b $内联$
需要这样的曲线才能在有限域上构造循环子组。 因此，正在使用以下参数：

• 素数$$ $内联$ p $内联$ 指定有限域的大小；
• 系数$$ $内联$ a $内联$ 和$$ $内联$ b $内联$ 椭圆曲线方程；
• 基点$$ $内联$ g $内联$ 产生提到的子组；
• 订单$$ $内联$ n $内联$ 分组中的
• 辅因子$$ $内联$ h $内联$ 子组中的

总而言之，我们算法的域参数是sextuplet$$ $内联$（p，a，b，G，n，h）$内联$ 。
这种椭圆曲线在有限域上起作用$$ $内联$ \ mathbb {F} _p $内联$ ，在哪里$$ $内联$ p $内联$ 是一个相当大的素数。 所以我们有一组整数取模$$ $内联$ p $内联$ ，其中可以执行加法，减法，乘法，加法逆运算，乘法逆运算等运算。 加法和乘法的工作方式类似于我们在RSA“环绕式封装”中看到的模块化或所谓的“时钟”算法。
由于曲线是关于x轴对称的，因此给定任何点$$ $内联$ P $内联$ ，我们可以$$ $内联$ -P $内联$ 正好相反。 我们采取$$ $内联$ -O $内联$ 只是$$ $内联$ O $内联$ 。
曲线点的加法定义为给定点$$ $内联$ P $内联$ 和$$ $内联$ Q $内联$ ，我们可以画出与这些点相交的线和与第三点相交的曲线$$ $内联$ R $内联$ 这样$$ $内联$ P + Q = -R $内联$ 和$$ $内联$ P + Q + R = 0 $内联$ 。

让我们看一下Marc Hughes的解释 ：

上面显示了一条沿着圆环表面的恒定斜率线。 这条线穿过曲线上的两个随机选择的整数点。



要在图形上添加两个点，请从第一个选定点绘制一条线$$ $内联$ P $内联$ 到第二个选定点$$ $内联$ Q $内联$ ，并延长线直到与图上的另一个点相交$$ $内联$ -R $内联$ ，并在必要时将其扩展到整个绘图边界。

截取整数点后，将点垂直垂直于图形的中间（橙色虚线）以找到新点$$ $内联$ R $内联$ 在图上。 因此$$ $内联$ P + Q = R $内联$ 。

标量的乘积现在是微不足道的：$$ $内联$ n \ cdot P = P + P + P + \点+ P $内联$ （这是$$ $内联$ n $内联$ 要求）。

这里的活板门函数位于离散对数（对于椭圆曲线）问题中，而不是我们在RSA部分中看到的分解。 问题是：如果我们知道$$ $内联$ P $内联$ 和$$ $内联$ Q $内联$ ，这是什么$$ $内联$ k $内联$ ，$$ $内联$ Q = k \ cdot P $内联$ ？

分解问题（位于RSA之下）和椭圆曲线的离散对数（这是ECDSA和ECDH的基础）都被认为很困难，即对于给定的密钥，在多项式时间内没有解决此问题的已知算法长度。

通常，虽然任何人都将密钥交换（ECDH）与签名（ECDSA）算法混合在一起会感到羞耻，但我们需要解释一下它们如何协同工作。 在我们的情况下，现代TLS证书包含一个由椭圆曲线算法生成的密钥对的公钥，通常由更高级别的权威机构签名。 客户端验证服务器的签名并获取共享密钥。 共享机密用于对称加密算法，例如AES或ChaCha20。 但是，原理仍然是相同的：同意域参数（sextuplet），获得密钥对，其中私钥是随机选择的整数（来自$$ $内联$ Q = k \ cdot P $内联$ ），而公钥是曲线上的一个点。 签名算法使用基点$$ $内联$ g $内联$ ，这是大质数阶子组的生成器$$ $内联$ n $内联$ ，这样$$ $内联$ n \ cdot G = 0 $内联$ ，其中0是标识元素。 签名证明与正当方建立了安全连接-服务器具有由某些证书颁发机构为给定服务器名称签名的TLS证书（公钥）。

（EC）DH（E）+ ECDSA =当前的握手形式

在现代TLS（1.3）中，客户端和服务器在建立连接的同时会动态生成其公私密钥对，这称为密钥交换的临时版本。 最流行的浏览器TLS库支持此功能。 大多数情况下，它们使用由Daniel J. Bernstein（djb）引入的Edwards 25519椭圆曲线 ，提供128位安全性。 从2014年开始，openssh使用此曲线创建密钥对。 但是在2019年，浏览器仍然不支持具有带有EdDSA公钥证书的服务器的TLS会话。

但是让我们回到TLS 1.3在2019年底的工作方式。

TLS 1.3中的密钥交换机制仅限于基于（EC）DH（E）的机制（x25519是大多数流行浏览器的客户端TLS库以及服务器端TLS库（如OpenSSL， （我们将在稍后进行检查），并且密码套件列表仅包含三个条目：TLS_AES_128_GCM_SHA256，TLS_AES_256_GCM_SHA384和TLS_CHACHA20_POLY1305_SHA256。 对于那些了解TLS 1.2版本中密码套件的命名方式的人来说，很明显，密钥交换机制现在已与密码套件名称“分离”，还删除了静态RSA和静态Diffie – Hellman交换模式。完全来自规范。 即使是基于PSK的会话恢复也是在TLS 1.3中通过ECDHE进行的。 对于自定义DH参数（现在不允许使用）也是如此，仅保留最终协议规范中普遍认为安全的那些参数。

有趣的是，当今非对称加密算法的工作方式存在相当大的差异。 与RSA相比，有了ECC（尤其是ECDSA证书），我们可以使用较小的密钥来达到“便捷”的安全级别。 这样就可以在较小的设备上，甚至在通常不被视为设备（智能卡）的设备上使用更强大的非对称加密算法和密钥交换机制。

首先，有必要提及TLS 1.3中的“混合密码系统”的含义。
混合密码系统是一种使用非对称（公共密钥）加密来建立共享机密的系统，该系统还用作对称流或分组密码中的密钥。

其次，公钥基础结构和证书。 有趣的是，马丁·赫尔曼（Martin Hellman）在2004年的采访中提到了“无名英雄”洛伦·科恩菲尔德（Loren Kohnfelder），他的麻省理工学院学士学位论文介绍了我们现在称为公钥基础结构的树形结构。 不过，让我们回退到证书。

服务器确实具有私钥这一事实是通过其签名来确保的，可以通过服务器公钥进行验证。 并且证书可确保某些公钥属于特定服务器。 这意味着您正在与特定方而不是冒名顶替者建立安全的通信。 您的银行，而不是网络犯罪分子。 在TLS 1.3中，对以前的协商格式进行了重大改进-服务器对到目前为止拥有的所有信息进行签名：客户端问候和服务器问候，包括协商的密码。 让我们看一下RFC 8446的相应部分：

Client Server Key ^ ClientHello Exch | + key_share* | + signature_algorithms* | + psk_key_exchange_modes* v + pre_shared_key* --------> ServerHello ^ Key + key_share* | Exch + pre_shared_key* v {EncryptedExtensions} ^ Server {CertificateRequest*} v Params {Certificate*} ^ {CertificateVerify*} | Auth {Finished} v <-------- [Application Data*] ^ {Certificate*} Auth | {CertificateVerify*} v {Finished} --------> [Application Data] <-------> [Application Data] 

在TLS 1.3中，客户端立即在第一条消息（客户端Hello）中发送密钥共享（以及所需的参数）和签名算法。 与服务器交换所需的密钥是在后台创建的，用户甚至没有注意到这一事实。 它们进一步与服务器交换，以根据服务器发送其消息（服务器Hello）来答复客户端时建立的预主密钥来创建公共密钥。
在“服务器Hello”侧，您可以看到证书*正在转移到客户端，以及证书验证*部分，该部分验证当事方拥有对应公共密钥条目的私钥，并在创建会话（对称）密钥时一切按计划进行-意思是，请求数据的一方（客户端）成功验证了应答方（服务器），从而进一步创建了一个公共机密。

此传输中隐藏了两个基本操作-签名创建和签名验证。 之所以在通信的两面进行，是因为“签名”本质上是证明该方实际上具有与公钥相对应的私钥，该数据来自签名者并且该消息在传输过程中没有被更改。

正如我们将进一步看到的，使用RSA，签名操作是最昂贵的。 由于我们使用的是2048位或3072位长的密钥进行签名，因此，这样的操作将显着加载服务器，远远超过了验证此类签名的客户端加载。

使用ECDSA，我们可以使用较小的密钥（我们将使用NIST P-256（或secp256v1）查看ECDSA），但操作更为复杂。 结果，它可以看作是“上下颠倒”的RSA-签名验证计算可以最大程度地负载客户端，而服务器则可以轻松地处理签名创建。 测量结果证实了这一点，请参阅“一些基准”部分。

这种效果可以轻松扩展当今的Internet，因为现代客户端几乎与服务器具有同等的功能（仅考虑CPU核心频率），因此它们可以有效地消除昂贵的操作。 反过来，服务器可以使用释放的功能来创建更多签名并建立更多会话。

让我们加密证书签名

因此，为了向读者提供一些实用且方便的说明，说明如何使用由Let's Encrypt权威机构签名的ECDSA密钥对创建启用TLS的服务器，我们决定说明创建所需密钥对的完整过程。为Let's Encrypt创建CSR（证书签名请求），并因此为我们的服务器获取所需的ECDSA证书。

我们必须生成一个私钥才能继续。 我们将使用OpenSSL库。
OpenSSL手册通过特殊命令描述了任何EC密钥的生成，该命令特别指定了生成算法的椭圆曲线分支。

 openssl ecparam -genkey -name -secp256v1 -out privatekey.pem 

要检查OpenSSL库是否正确执行了所有操作，我们可以执行ec命令。

 openssl ec -in privatekey.pem -noout -text 

输出将向我们显示已创建关键点的指定曲线。

下一步对于创建CSR非常重要-为了跳过填写获得证书所需的所有信息详细信息的过程，我们需要配置文件。 幸运的是，Mozilla为我们做了整个工作，引入了“ SSL配置生成器 ”。 在那里，您可以从任何可用的服务器选项中进行选择。 纯粹在生成器页面上不存在的OpenSSL配置看起来像这样：

 [ req ] prompt = no encrypt_key = no default_md = sha256 distinguished_name = dname req_extensions = reqext [ dname ] CN = example.com emailAddress = admin@example.com [ reqext ] subjectAltName = DNS:example.com, DNS:*.example.com 

注意：不需要CNF-如果没有，则将要求您在命令行中填写这些详细信息。

现在，遵循CSR本身的创建。 在这里，我们有一个方便的OpenSSL命令。

 openssl req -new -config -pathtoconfigfile.cnf -key privatekey.pem -out csr.pem 

我们还可以验证新创建的CSR的正确性。

 openssl req -in csr.pem -noout -text -verify 

在这里，我们进入了最后阶段-使用ACME客户端certbot将我们的证书签名请求传递给Let's Encrypt。

Certbot可帮助您获得所需的证书，并有很多选择。 这里说的是，如果您不--dry-run公钥加密以及我们在2019年拥有的PKI基础结构，则在尝试获取您任何域的证书之前，最好使用--dry-run 。

 certbot certonly --dry-run --dns-somednsprovider --domain “example.com” --domain “*.example.com” --csr csr.pem 

在这种情况下，certbot客户端会检查（在命令行中）请求的域列表是否与证书签名请求中列出的域匹配。 在--dns-somednsprovider命令中有一个谎言，因为有很多方法可以证明“让我们加密”是您拥有Internet流量的特定部分。 但是，如果您使用的是某些公共云托管提供商，例如DigitalOcean，Hetzner，Amazon，Azure等，则可能会提供一种更自然的方式来提供所需的信息，因为您的提供商已经制作了一些集成工具。

之后，如果您确定通过certbot客户端将CSR传递给Let's Encrypt时所用参数的正确性，请在命令中排除--dry-run参数，然后继续。

如果成功，则客户端将生成多个证书作为输出：签名证书本身，根证书和中间证书，以及后者的组合作为姓氏证书链，所有文件均采用.pem文件格式。

OpenSSL具有可用于检查证书的命令：

 openssl x509 -in chainfilepath.pem -noout -text 

在这一点上，很明显，Let's Encrypt使用SHA256摘要对证书进行了签名。 此外，ECDSA根目录和中间件签名属于“即将推出的功能”部分，这实际上意味着，现在您仅会获得RSA中间件。 但这没关系，因为您仍在使用ECDSA公钥。

在本节的最后，我们想说一些与键的长度有关的内容。 在信息安全中，通常说安全级别是2 ^ x，其中x是位长（RSA在这里有点例外，因为它的增长比指数增长要慢）。 要估算用于不同算法的密钥如何相互对应，请参考OpenSSL Wiki页面 。
如您所见，差异非常明显。 尽管使用Let's Encrypt，我们无法在256（secp256v1）和384（secp384r1）椭圆曲线密钥之外获得任何签名的证书。

已知问题和例外以及国家安全局

积分： xkcd

多年来，使用椭圆曲线密码学的中心问题可能是需要精心设计的随机数生成器，以便创建所需安全级别的密钥。

Dual_EC_DRBG （双椭圆曲线确定性随机位生成器）算法周围发生了大规模丑闻，解决了许多年。 此外，ECC专利存在不确定性，因为众所周知，其中许多专利属于Certicom公司，该公司被黑莓（Blackberry）收购。 也有一些公司被黑莓公司证明可以使用ECC。 当然，在某些NIST标准中存在简单的不信任感，这些标准可能会受到美国国家安全局（NSA）或美国任何其他执法和监视机构的影响。

问题的实现方面是一个完全不同的问题。 2010年，由于ECDSA算法的实施不正确，PlayStation 3控制台遭受了索尼私钥恢复，因为它们具有静态随机性，因此可以解决活板门功能。 但是，OpenSSL在第二年也遭受了损失，但很快修复了该漏洞，该漏洞允许在定时攻击的帮助下检索私钥，有关更多信息，请参阅原始文章 。

2013年，在RSA会议上，一组研究人员展示了他们的“ 随机失败！ 有关SecureRandom Java类漏洞的论文。 半年后，它归结为使用加密安全性不足的PRNG创建的Android 比特币钱包。

由于发现了严重的串行漏洞，2013年8月，IETF发布了RFC 6979 ，描述了密钥创建中使用的确定性k代。 我们可以说这样的措施可以解决问题，但是我们不会-由于与协议规范的不必要偏离，研究人员在任何时候都可以在众多实现中发现问题。

关于国家安全局。 如果您还没有听说过Dual_EC_DRBG的故事-请花些时间阅读相关文章，您将不会后悔获得详细信息。 爱德华·斯诺登（Edward Snowden）是这个故事的一部分，因为2013年的披露证明了早先的怀疑。 由于该组织设计并描述了ECDSA的许多曲线和其他算法，因此导致许多杰出的密码学家对NIST失去信任。

丹尼尔·伯恩斯坦（Daniel Bernstein）的25519曲线和DH函数可同时解决这两个问题，而且正如我们之前所述，向EdDSA的过渡虽然缓慢，但显而易见。 即使使用NIST曲线，也尚未发现其脆弱性的证据，而且正如我们已经提到的，与随机相关的经验也很有启发性。

总结这一部分，我们想引用约翰·冯·诺伊曼的话：“任何试图通过确定性手段生成随机数的人，当然都处于犯罪状态。”

有点基准

我们使用带有OpenSSL 1.1.1d的NGINX 1.16.0服务器使用各种证书运行这些基准测试。 如前所述，当前的“加密”仅允许prime256v1和secp384r1算法用于证书签名请求，并且不提供根ECDSA证书和中间ECDSA证书，在我们撰写本文时，此功能可能起作用。
如您所见，对于英特尔®至强®银牌4114 CPU @ 2.20GHz（17年第三季度发布），与广泛采用的RSA 2048相比，ECDSA性能的总体差异为3.5倍。

现在，让我们看看使用ECDSA和RSA的同一处理器的OpenSSL -speed结果。
在这里，我们可以看到对早期给出的确认的证明，该论文针对ECC和RSA的符号和验证操作使用了不同的计算成本。 结果，与RSA相比，当前配备TLS 1.3 ECC的设备在更高的比特安全级别上提供了显着的性能提升。 这就是我们Qrator Labs鼓励客户采用ECDSA的最重要原因。 使用现代CPU，您获得ECDSA的收益几乎是5倍。

如果您对CPU如何执行密码计算感兴趣，可以运行一个简单的openssl speed命令。 -rsa ， -ecdsa和-eddsa参数将为您提供相应签名算法的基准测试结果。

（叠加）未来

积分： djb

具有讽刺意味的是，当我们准备本文时，谷歌宣布“ 达到量子霸权 ”。 这是否意味着我们现在处于危险之中，并且到目前为止所开发的一切都没有提供任何保密性？

好吧，不。

正如布鲁斯·施耐尔（Bruce Schneier）在他的IEEE安全和隐私文章“ 外星人之后的密码学 ”中所写的那样，可以用足够强大的量子计算机对公钥（非对称）密码学造成巨大的打击。 对称密码学仍然很强大。

我们想用以下内容引用Bruce Schneier的话：

还有另一种需要考虑的未来情况，即不需要量子计算机的情况。 尽管有几种数学理论支持我们在密码学中使用的单向性，但证明这些理论的有效性实际上是计算机科学中的一个巨大开放问题之一。 就像聪明的密码学家可能找到一种使破解特定算法更容易的新技巧一样，我们可能会想象外星人具有足够的数学理论来破解所有加密算法。 对于我们来说，今天，这是荒谬的。 公钥密码学是所有数字理论，并且可能容易受到数学上更倾向于外星人的攻击。 对称密码学是那么多非线性的混乱，容易使它变得更加复杂，并容易增加密钥长度，以至于这种未来是无法想象的。 考虑具有512位块和密钥大小以及128个回合的AES变体。 除非数学与我们当前的理解有根本不同，否则除非计算机由物质以外的东西组成并且占据空间以外的东西，否则这将是安全的。

但是，如果发生了无法想象的事情，那将使我们只能使用基于信息论的密码学：一次性垫及其变体。

在此区域中，除了寻找实现缺陷之外，大多数问题都可以找到。 如果有一群资金雄厚的数学家，密码分析家/密码学家和计算机工程师致力于证明或证明某些非常复杂的数学问题（例如P？= NP）并在此之前取得实质性成果，我们可能会遇到麻烦。 但是，计算机科学，信息和可计算性理论方面的这种进步不太可能被隐藏，因为该事实会将其创建者的姓名写在历史，尤其是互联网教科书的页面上，这对于任何聪明的人来说都是无价的。 。 因此，几乎不可能消除这种情况。

目前尚不清楚，在最近的五年中，量子计算是否会取得成功，尽管已经有几种密码学原语被认为适合后量子世界：网格，基于奇异性的椭圆曲线基于等遗传学，哈希和代码。 目前，安全专家正在对其进行试验。 但是，毫无疑问，在需要的情况下，人类将迅速大规模地采用这种算法。

就目前而言，基于椭圆曲线的密码学似乎非常适合未来十年，提供了安全性和性能。