椭圆曲线加密在TLS 1.3中的工作方式

给读者一些警告：

为了（尽可能）简化解释过程并压缩出版物数量，有必要立即保留一个关键的保留-我们所写的有关问题实际内容的所有内容对于TLS协议1.3版都是正确的。 这意味着，尽管您的ECDSA证书（如果需要）可以与TLS 1.2一起使用，但是握手过程，密码套件和基准的描述是基于TLS协议的最新版本1.3进行的。 如您所知，这不适用于构成现代密码系统基础的算法的数学描述。

尽管他们帮助铺平了数学丛林的道路，但这些材料不是由数学家甚至工程师撰写的。 非常感谢Qrator Labs的工作人员。

（椭圆曲线）Diffie- Hellman（短暂）

21世纪Diffie-Hellman传统

自然，这个主题不是以Whitfield Diffie开头，也不是以Martin Hellman开头。 艾伦·图灵（Alan Turing）和克劳德·香农（Claude Shannon）对算法和信息论以及密码分析领域做出了巨大贡献。 反过来，Diffie和Hellman也被公钥密码学（也称为非对称）思想的作者正式认可-尽管现在众所周知，在英国，这一领域也取得了重大成果。 但是，他们长期以来一直是秘密的-这使得副标题中提到的两位先生成为先锋。

到底是什么

这似乎很有趣，但是直到1976年11月6日，才没有有关公钥密码系统的知识。 数学家，计算机工程师和发烧友以及密码学家Whitfield Diffie和Martin Hellman（实际上是Ralph Merkle）以及密码学家都率先提出了一个合适的概念。

在第二次世界大战期间，密码术有助于将信息保密，而密码分析则有助于将其泄露。 美国和英国认为自己是密码学领域中最先进的。 这两个国家在武器部分中包括了加密算法，并否决了其出口。 同时，在这些国家/地区已放宽了用于商业或家庭用途的可用加密。 出于这个原因，直到1997年，当时对加密算法及其描述的现有限制都失去了所有意义，英国研究人员在政府通信中心（GCHQ）从事非对称密钥分配方案并开发类似概念的研究人员才得到社区的认可。在道德上已经过时。

回到我们这对发明家中-Diffie和Hellman究竟发生了什么革命？

为了解释这一点，让我们看一下原始出版物中的插图，它完美地反映了在理解密码学如何工作方面的巨大飞跃-即使只是从理论上来说也是如此：

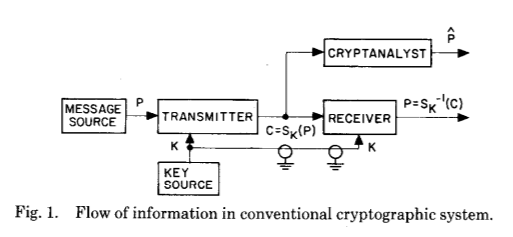
现在针对以下内容：

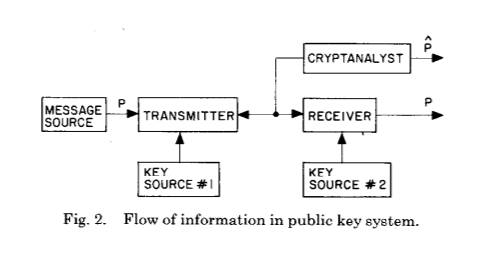
这两张图片显示了经过数百年的密码学和密码分析发展，惠特菲尔德·迪菲（Whitfield Diffie）和马丁·赫尔曼（Martin Hellman）的主要创新-通过某种类型的计算建立了一个共同的秘密。

让我们看一下维基百科的另一张图片，其中不同的颜色被用作秘密：



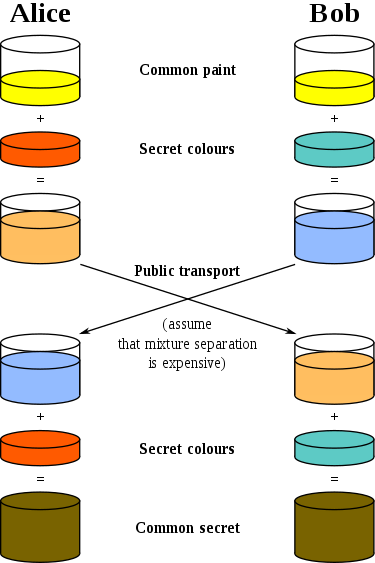
她还很好地解释了正在发生的事情。 在Diffie和Hellman创新之前，只有一种以公共密钥建立方案的形式存在的公共密钥-用于加密和解密消息。 如果要将这样的密钥传送到第二面，则必须通过最初受保护的通道进行传输。 这种方案的所有局限性立即变得清晰起来-您需要一个安全的（来自侦听的）通信通道，不能多次使用同一密钥，并且理想情况下，密钥长度应与消息的长度相对应。

克劳德·香农（Claude Shannon）在其后来解密的著作“秘密系统中的通信理论”中，证明了所有理论上不可破解的密码必须具有与一次性密码块（也称为Vernam密码）相同的属性，并使用这种加性多字母流加密算法的创建者的名字。

再来看看原始的科学出版物：


在继续进行之前，让我们问一个显而易见的简单问题：两个人，即使是非常聪明的人，如何在应用领域取得如此突破，特别是考虑到战时的巨大成功？ 最有可能是由于当时积极发展的以下领域的结合：

• 克劳德·香农提出的信息论；
• 算法理论受到Alonzo Church，John von Neumann和Alan Turing等人的影响；
• 而且，最重要的是， 可计算性理论主要基于图灵的工作。

可以说，所有这些领域都是在20世纪同一时期发展和成熟的。 迪菲（Diffie）和赫尔曼（Hellman）还提到克劳德·香农（Claude Shannon），他是一个对工作影响最大的人物。

Arjen Lenstra的“通用安全性”概念表明，用不同长度的密钥“破解”对称密码系统需要花费多少精力。 事实证明，要破解基于椭圆曲线的算法的228位密钥，您需要的能量足以将地球上的所有水加热到沸点。 但是，仅当我们考虑众所周知的算法并使用现代设备时，该声明才是正确的，因为严格来说，可以使用更高效的算法或设备，但它们的存在尚不为人所知。 EC算法用于破解复杂性的228位密钥与RSA中的2380位密钥相当，但以后会更多。 在此比较中，RSA和EC密钥用于非对称密码系统中，在对称方案中可以认为它们等效于128位密钥。

很难想象，“难以计算”的东西将需要大量的时间和精力来计算。 我们倾向于认为计算机可以“计数任何东西”，但事实证明，这远非事实。

首先，有一些无法解决的问题，例如停止问题。 但是，在密码学领域中，没有使用这些任务。

其次，如果我们考虑特定算法所需的运行时间，那么它可能会很大。 这正是密码学所使用的。 如果相应算法工作所需的时间取决于多项式输入数据的大小（以位为单位），则认为该任务在计算上“简单”： $$$T（n）= O（n ^ k）$对于一些积极 $$$k$。 在计算复杂性理论中，此类问题形成了复杂性类别P。如果算法的运行时间比多项式增长得更快（例如，按指数增长），则该任务在计算上被认为是“困难的”。

复杂度类别P包含任务，该任务具有确定性算法，该算法可以在多项式时间内工作。 NP的另一种复杂性类别（其中可能存在“困难”问题）是NP的可解决性问题，即需要答案为“是”或“否”的问题，其答案的正确性可以得到验证-即，提供解决方案正确性的证明-在多项式时间内。 在这里看到“证明”一词吗？ 这是我们传递给单边函数的地方，这些函数的求逆问题属于复杂度类NP。


发言者： xkcd

（单向功能（带有秘密输入））

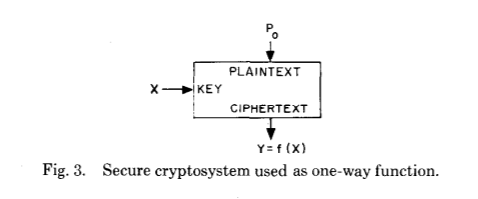
根据定义，单向函数是一种易于为任何输入计算但又难以求逆的函数，即仅获得结果的原始输入。 “容易”和“困难”是指上述计算复杂性的理论。 有趣的是，单向函数的存在（数学上）尚未得到证明，因为对其存在的严格证明还将证明P和NP类的不等式，千年问题和紧迫的开放问题之一，其解决方案有望实现算法上的突破。 因此，有必要记住，几乎所有现代加密技术都是基于未经证实的假设。

Diffie和Hellman在其原始出版物中介绍了新一代的单向功能，称其为“带有秘密输入的单向功能”-英语陷井功能。 它们与单向功能有何不同？

让我们看看他们的原始解释：

在具有公共密钥的密码系统中，加密和解密分别由各种密钥E和D执行，因此从E计算D实际上是不可能的（例如，要求 $$$10 ^ {100}$说明）。 可以公开披露加密密钥E而不会破坏密钥D。这允许任何系统用户向任何其他用户发送消息，并以只有预期的接收者可以解密的方式进行加密。 与密钥的分配相比，身份验证任务可能是业务交易中更为严重的电信问题，因为它是（身份验证）位于任何处理合同和付款的系统的核心。

通常，使用密码字符Alice和Bob来解释密码系统操作的原理（他们致力于安全通信）。 爱丽丝和鲍勃同意选择大素数 $$$n$和 $$$g$这样 $$$1 <g <n$。 这种选择会影响整个电路的安全性。 编号 $$$n$称为模块应该很简单； 此外，数量 $$$（n-1）/ 2$也应该很简单，但是 $$$g$必须是残基模群中的原始根 $$$n$; 另外 $$$n$应该足够大-至少以512位二进制表示。 此外，可以通过五个简单步骤描述Diffie-Hellman协议：

1. 爱丽丝精选 $$$x$（大素数）并计算 $$$X = g ^ x \ bmod n$
2. 鲍勃·皮克 $$$y$（也是很大的素数）并计算 $$$Y = g ^ y \ bmod n$
3. 爱丽丝发送 $$$X$鲍勃，鲍勃发送 $$$Y$爱丽丝（ $$$x$和 $$$y$他们每个人都是秘密）
4. 爱丽丝计算 $$$k = Y ^ x \ bmod n$
5. 鲍勃正在计算 $$$k'= X ^ y \ bmod n$

结果，Alice和Bob在构造上得到了相同的结果。 $$$k = k'$-一个共享的秘密。

因此，具有秘密输入的单向功能就是这样一种单向功能，可以通过拥有一条称为“秘密输入”的特殊信息来逆转。 这听起来很简单，但实际上在实践中发现找到这样的功能并不是一件容易的事-第一个像样的方法竟然是基于一个以其创建者名字命名的，名为RSA的公钥的整个算法系列的先驱者。

RSA

在RSA中，函数求逆的复杂性是基于以下事实：因式分解（数的因式分解）比乘法花费的时间长得多，或者更确切地说，可以说，在经典计算机上找不到用于分解多项式时间中的大数的方法，尽管它不是事实证明，这种算法是不存在的。

在RSA中，就像其他任何具有公钥的加密系统一样，有两个密钥：公钥和私钥。 RSA算法采用由位串表示的输入消息，并对其进行数学运算（以幂为模的幂），以获得与随机无可区别的结果。 对于解密，获取结果并执行类似的操作以接收原始消息。 在非对称密码学中，使用公共密钥执行加密，然后使用私有密钥进行解密。

这怎么可能？ 由于使用的值属于一个有限循环组（在模算术中带有乘法的整数集），因此这一事实。 计算机不能很好地处理任意大的数字，但是循环组的属性是“环绕”的-大于允许的最大值的数字被“包装”为允许的值。 这使我们可以使用长度不超过一定位数的密钥。 在基于椭圆曲线的密码学中，还使用了循环（乘法）组，但是它们的构造略有不同，我们将在后面看到。

在非常原始的级别上，RSA所做的全部就是取两个大素数，将它们相乘得到所谓的模块。 将要执行操作的所有其他数字应在零和模块值之间。 模块本身将成为公共密钥的一部分-它的长度决定了密钥的长度。 公钥的第二部分是从零到模块中的Euler函数（现代RSA实现使用Carmichael函数而不是Euler）的值之间选择的数字，还有一些其他限制。 最后，您可以通过求解模块化方程来计算私钥。 为了加密消息，我们用代表消息的数字并将其简单地提高到等于公钥值的幂，然后对其进行解密-接收原始消息，将其提高到等于私钥值的幂。 由于组的周期性，我们得到相同的含义。

如今，RSA有两个主要问题，其中一个是另一个问题的结果。 随着密钥长度的增加，复杂性不会像我们期望的那样快速增长。 这是因为存在次指数（但仍是超多项式） 分解算法。 因此，为了维持必要的保护级别，RSA密钥的长度应比ECC密钥的长度增长得更快。 因此，当今最常见的RSA密钥长度非常大：2048位和3072位。

稍后，我们将通过比较Let's Encrypt RSA和ECDSA签署的证书，在特定的数字上看到密钥长度如何影响密码系统的最终性能。

椭圆曲线数字原位算法

为了通过秘密输入寻找更可靠的功能，80年代中期，密码学家开始使用专门研究椭圆曲线的数学分支。

在一个文本中描述基于椭圆曲线的密码学的所有细节将太困难了，因此我们不会这样做。 相反，让我们看一下基于椭圆曲线和离散对数问题构建的单向秘密输入函数。

关于密码学领域，有大量的复习材料和更详细的介绍。 我们想指出Andrea Corbellini的“ ECC：简要介绍” ，尤其是如果您对该设备感兴趣的话。

在本文中，我们对更“简单”的解释感兴趣。
椭圆曲线由如下所示的方程式定义： $$$y ^ 2 = x ^ 3 + ax + b$。

第二个对象是有限域上的循环子组。 ECC算法中使用以下参数：

• 素数 $$$p$，它确定最终字段的尺寸；
• 赔率 $$$一$和 $$$b$椭圆曲线方程；
• 基点 $$$G$生成已经提到的子组；
• 订购 $$$n$亚组
• 辅因子 $$$h$亚组。

结果，我们算法的参数集由六个表示 $$$（p，a，b，G，n，h）$。

椭圆曲线的点属于有限域 $$$\ mathbb {F} _p$在哪里 $$$p$这是一个相当大的素数。 所以，我们有很多整数取模 $$$p$可以进行加，减，乘，反运算的操作。 加法和乘法的工作方式与我们根据RSA（环绕式）部分的模块化算术描述方式类似。

由于曲线关于x轴对称，因此对于任何点 $$$P$我们可以拿 $$$-P$并得到与之相反的观点。 我们立即规定 $$$−O$对应于零，即 $$$−O$会很简单 $$$O$。

定义曲线上的点的加法，以便知道这些点 $$$P$和 $$$Q$，我们可以画一条穿过这两个点的线以及第三个点- $$$R$这样 $$$P + Q = -R$和 $$$P + Q + R = 0$。

让我们看一下马克·休斯的插图：

我们看到一条沿圆环表面延伸的直线。 该线与曲线上的两个随机选择的点相交。



为了找到 $$$R$，我们从第一个选定点画一条线 $$$P$到第二 $$$Q$继续直线直到它在第三点处穿过曲线 $$$-R$。

相交之后，反射相对于横坐标轴的点以找到该点 $$$R$。

标量的乘法很明显地确定为： $$$n \ cdot P = P + P + P + \点+ P$。

在这种情况下，具有秘密输入的单向函数依赖于椭圆曲线的离散对数问题，而不是像RSA那样依赖分解。 在这种情况下，离散对数问题的公式如下： $$$P$和 $$$Q$，然后如何找到 $$$k$这样 $$$Q = k \ cdot P$？

分解问题（这是RSA的基础）和椭圆曲线的离散对数（这是ECDSA和ECDH的基础）都被认为很困难-换句话说，对于给定的密钥长度，在多项式时间内没有解决这些问题的算法。

尽管通常情况下，我会被肮脏（最好）的碎布轰炸，以将签名分发算法（ECDH）与签名（ECDSA）混合使用，但我仍然必须解释它们是如何协同工作的。在我们的情况下，现代TLS证书包含一个公钥，该公钥是使用基于椭圆曲线的算法生成的一对，通常由某些权威组织签名。客户端验证服务器签名并生成共享机密。此机密用于AES或ChaCha20等对称加密算法中。但是，基本原理保持不变：同意一组（六个）参数，获得一个密钥对，其中私钥是随机选择的整数（$$），和公共密钥-这是曲线上的点。签名算法使用基点$Q=k\cdot P$$$是阶次子集的生成器$G$$$$n$ （ $$是一个大素数），所以$n$$$，其中0 -的基团的中性元素。签名证明与被认证方建立了安全连接-服务器具有由权威组织针对给定服务器名称签名的TLS证书（公钥）。$n\cdot G=0$

（EC）DH（E）+ ECDSA =现代形式的握手

在现代TLS版本1.3中，客户端和服务器会动态生成密钥对，从而建立连接。这称为密钥交换算法的“临时”版本。最受欢迎的TLS库仅支持这种协议版本。大多数情况下，今天使用的是由Daniel Bernstein Jr.（djb）提出的Edwards椭圆曲线25519，它提供了128位的保护级别。自2014年以来，该曲线可用于在openssh库中创建密钥对。但是，截至2019年底，浏览器仍未使用EdDSA签名算法的公钥与服务器建立TLS会话。

让我们看一下TLS 1.3中的所有功能。

在该协议的最新版本中，密钥分发机制仅限于（EC）DH（E）-x25519是获取共享密钥的最常用功能-大多数浏览器和服务器TLS库均支持此功能。密码套件仅包含三个条目：TLS_AES_128_GCM_SHA256，TLS_AES_256_GCM_SHA384和TLS_CHACHA20_POLY1305_SHA256。对于那些熟悉在先前版本的协议TLS 1.2中如何命名密码套件的人来说，很明显，在向TLS 1.3过渡期间，密钥交换机制的指示是与密码套件“分开的”。同样，静态RSA和DH密钥交换方法也被排除在规范之外。甚至在TLS 1.3中借助PSK和上一会话的票据进行的会话恢复都使用ECDHE协议进行，在该协议中，最后的E-星历特别重要。同样，在TLS 1.3中，无法为Diffie-Hellman机制设置您自己的值-协议规范中仅保留了预定义的集合，关于该集合的安全性已达成共识。

特别令人感兴趣的是，现代非对称加密机制的工作原理有所不同。在ECC中（特别是在使用ECDSA证书时），我们使用与RSA相比长度较短的密钥，以达到可接受的安全级别。这样，即使在似乎没有足够能力执行必要操作的设备（例如智能卡）上，您也可以使用强大的非对称加密和密钥交换方案。

首先，有必要弄清楚术语“混合密码系统”在TLS 1.3的描述中的含义。混合密码系统使用非对称（具有公钥）加密方案来建立共享机密，然后将其用作对称块或流加密算法中的密钥。

其次，存在公共密钥（PKI）和证书（CA）的基础结构。有趣的是，马丁·赫尔曼（Martin Hellman）在2004年提到了“无名英雄”之一劳伦·科恩费尔德（LaurenKönfelder），其捍卫麻省理工学院学士文凭的论据是创造树形结构的可能性-我们今天将其称为PKI。但是，让我们回到证书上来。

服务器真正拥有私钥的事实通过其签名进行了验证，可以使用公钥进行验证。服务器上的证书文件证明特定的公共密钥属于特定的服务器。这意味着您正在与所需的对话者建立安全连接，而不是冒充者-您的银行，而不是网络欺诈。

与该协议的先前版本相比，TLS 1.3大大改进了协商方案。现在，服务器会在创建此类签名时对握手中收到的所有信息进行签名：客户端问候和它自己的服务器问候以及选择使用的一组密码。让我们看一下RFC 8446中交互描述的相应部分：

Client Server Key ^ ClientHello Exch | + key_share* | + signature_algorithms* | + psk_key_exchange_modes* v + pre_shared_key* --------> ServerHello ^ Key + key_share* | Exch + pre_shared_key* v {EncryptedExtensions} ^ Server {CertificateRequest*} v Params {Certificate*} ^ {CertificateVerify*} | Auth {Finished} v <-------- [Application Data*] ^ {Certificate*} Auth | {CertificateVerify*} v {Finished} --------> [Application Data] <-------> [Application Data] 

在TLS 1.3中，客户端发送其部分密钥（以及必要的参数）和第一条消息中可用的签名列表（客户端Hello）。 在此阶段所需的密钥是由客户端动态创建的-用户甚至没有注意到这一点。 接下来，客户端和服务器交换此信息以创建一个共享密钥-一个会话密钥，该会话密钥是在服务器用其消息响应客户端（服务器Hello）后从接收到的主主对创建的（或更确切地说是派生的）。
在“服务器Hello”端，您可以看到与证书到客户端的传输相对应的记录（Certificate *），以及CertificateVerify *检查，它确认当事方确实具有与相应公钥记录相关的私钥，然后在其中创建会话（对称）密钥对。成功案例。 换句话说，数据请求方（客户端）已通过切换为使用共享机密来成功验证了响应方（服务器）的真实性。

在此传输中，保护了两个主要的密码操作-创建签名并验证签名。 这些操作通常在连接的不同端执行，因为大多数情况下，客户端会验证服务器的真实性。 签名本质上是对与公钥相对应的私钥所有权的确认。 也就是说，我们从签名人那里接收数据，并确保消息在传输过程中没有被更改。

当使用RSA算法时，正如我们稍后将在数字上演示的那样，创建签名的操作最昂贵。 由于我们使用2048或3072位密钥进行签名，因此这样的操作会显着加载服务器-在其（签名）验证期间比客户端强得多。

在ECDSA中，我们使用相对较短的密钥进行操作（在基准示例中，我们将使用NIST P-256曲线（或secp256v1）查看ECDSA，但是这些密钥涉及更复杂的操作。因此，使用ECC可以表示为具有以下特征的“反向” RSA：性能的观点：签名验证操作会给客户端带来更大的负担，而服务器会轻松地处理签名创建操作，正如我们在基准测试部分提供的度量所证明的那样。

这种效果有助于扩展Internet-由于现代客户端几乎与服务器一样强大（如果仅考虑处理器内核的时钟速度），它们可以有效地进行计算上困难的操作，而不会出现问题。 反过来，服务器可以使用释放的计算能力来创建更多签名，并因此建立更多会话。

让我们加密的证书签名

我们将为读者提供一个简单易懂的说明，您可以在其上独立创建一个服务器，该服务器能够使用ECDSA密钥对建立能够建立TLS会话的服务器，该密钥对是公开签名的Let's Encrypt并作为证书包含在信任链证书中。
我们决定显示从创建密钥到为Let's Encrypt创建证书签名请求（CSR）以及使用certbot实用程序发送签名以进行签名的完整路径，该实用程序将返回必要的链和ECDSA证书本身。

首先，您需要创建一个密钥对。 为此，我们将使用OpenSSL库。 《 OpenSSL用户指南》说，使用专用于基于椭圆曲线的算法系列的特殊命令来创建基于椭圆曲线的算法的密钥。

 openssl ecparam -genkey -name -secp256v1 -out privatekey.pem 

为了验证我们的团队是否正常工作，我们执行ec命令，指示指向包含私钥的新创建文件的路径。

 openssl ec -in privatekey.pem -noout -text 

输出应向我们显示所使用的曲线，并由此生成密钥。

在创建CSR时，下一步非常重要-为了不填写每次签署证书所需的问卷，我们需要一个配置文件。 幸运的是，几乎为我们完成的所有工作都是由Mozilla完成的，创建了“ SSL配置生成器 ”。 在其中，您可以从服务器模式的各种选项中进行选择，通过它们可以建立TLS连接。 由于某些原因，Mozilla生成器中缺少干净的OpenSSL配置，如下所示：

 [ req ] prompt = no encrypt_key = no default_md = sha256 distinguished_name = dname req_extensions = reqext [ dname ] CN = example.com emailAddress = admin@example.com [ reqext ] subjectAltName = DNS:example.com, DNS:*.example.com 

注意：您不必具有配置文件-如果该文件不存在，则将要求您填写命令行上的所有字段。 使用配置文件（在下一个命令中指定的路径），该过程得以简化。

接下来是证书签名请求（CSR）本身的创建。 为此，我们有一个方便的OpenSSL团队。

 openssl req -new -config -pathtoconfigfile.cnf -key privatekey.pem -out csr.pem 

我们还可以验证新创建的CSR的正确性。

 openssl req -in csr.pem -noout -text -verify 

最后，我们进入最后阶段-使用ACME客户端certbot，我们将转移我们对Let's Encrypt组织证书签名的请求。

Certbot不仅会帮助您获得证书，而且还有许多其他不错的选择。 我们补充说，如果您不熟悉使用公共密钥的加密，并且不真正了解当前存在的公共密钥基础结构，则最好在尝试为您的任何域获取真实证书之前使用--dry-run选项。

 certbot certonly --dry-run --dns-somednsprovider --domain “example.com” --domain “*.example.com” --csr csr.pem 

在这种情况下，certbot客户端会验证命令行上请求的必需域列表是否与证书签名请求（CSR）中的列表匹配。 在--dns-somednsprovider我们--dns-somednsprovider ，因为有很多方法可以确认让我们加密您拥有互联网流量的一部分。 但是，如果您使用诸如DigitalOcean，AWS，Azure，Hetzner之类的某种云提供商，则您可能已经有了一种更简便的方法来提供认证所需的信息，因为您的提供商已经在使用集成工具。

此后，如果您确定使用certbot传递给“让我们加密”的CSR参数正确，只需从命令中删除--dry-run参数，然后继续即可。

如果成功，客户端将向您返回几个证书：签名证书本身，中间证书和根证书，以及证书链形式的后者的组合，全部为.pem格式。

OpenSSL具有一个用于查看证书内部的命令：

 openssl x509 -in chainfilepath.pem -noout -text 

现在应该很清楚，让我们使用SHA256哈希算法对证书进行签名。 除此之外，Let's Encrypt仅计划将根签名和中间签名添加到ECDSA，因此到目前为止，它仍然满足于中间RSA签名。 但这并不可怕，因为无论如何您都将使用ECDSA公钥。

在本节的最后，我们想添加一些信息来比较各种算法的密钥长度。 在信息安全中，习惯上说安全级别是2 ^ x，其中x是位长（RSA是个例外，因为它的增长比指数慢一些）。 为了大致比较各种算法的密钥，我们参考OpenSSL Wiki页面：

如您所见，差异非常明显。 尽管目前为止，“加密”仅允许您在两条椭圆曲线的键-256（secp256v1）和384（secp384r1）上接收签名证书。

已知的困难以及国家安全局

发言者： xkcd

使用基于椭圆曲线的密码术的中心问题可能是需要非常整洁地实现的随机数生成器，这对于创建一定安全级别的密钥是必需的。

Dual_EC_DRBG算法引起了巨大的丑闻-解决它花了很多年。 围绕ECC的专利基础存在不确定性-众所周知，许多专利都属于Certicom，并被Blackberry收购。 还有一些已知的Blackberry ECC认证案例。 最后，人们对NIST标准存有某种不信任感，这可能会受到NSA或任何其他美国情报机构的影响。

密码标准实施中的错误是一个完全正交的话题。 2010年，由于ECDSA算法的实施不正确，PlayStation 3遭受了索尼私钥的泄漏-索尼无法应对RNG，并提供了相同的随机数，这使得通过秘密输入来解决该功能成为可能。 OpenSSL在第二年遭受了损失，但是它很快修复了一个漏洞，该漏洞使它可以使用时间攻击来获取私钥-有关更多详细信息，请参见原始研究出版物 。

在2013年的RSA会议上，一组研究人员发表了一篇名为“ 随机失败！ ”专用于SecureRandom Java类漏洞。 六个月后，事情开始于使用加密不安全的伪随机数生成器创建的比特币钱包 。

由于在短时间内发现了几个严重漏洞，因此IETF在2013年8月发布了RFC 6979 ，该文档描述了创建密钥时确定性地生成k的过程。 我们可以写出问题是通过这种方式解决的，但是我们不会-在任何时候，研究人员可能会由于不必要地偏离协议规范而发现实施中的新错误。

关于NSA的几句话。 如果您不了解Dual_EC_DRBG的历史-请花一些时间阅读相关材料，您将不会后悔找出细节。 爱德华·斯诺登（Edward Snowden）成为了这个故事的一部分，因为正是由于他在2013年的泄密，所有存在的疑虑才得以证实。 这导致许多杰出的密码学家对NIST失去信心，因为正是这个组织创造并描述了许多在ECDSA中工作的椭圆曲线和算法。

由丹尼尔·伯恩希特（Daniel Burnshite）编写的曲线25519和用于分配密钥的Diffie-Hellman函数是上述许多问题的答案。 而且，正如我们已经写过的，朝着EdDSA稳步发展。 在NIST曲线的情况下，尚未发现其脆弱性的确认，至于具有随机数的经验，这是非常痛苦的，并有助于快速同化。

在总结这一部分时，我们想引用约翰·冯·诺伊曼的话：“在获取随机数的算术方法上有弱点的任何人毫无疑问都是无罪的。”

一些基准

我们将NGINX 1.16.0服务器和OpenSSL库版本1.1.1d一起使用来对两个证书进行测试。 如前所述，目前，Let's Encrypt允许您仅使用prime256v1和secp384r1算法创建证书签名请求，并且不为根证书和中间证书提供ECDSA签名，这可能是您在阅读此说明时处理的。

如您所见，在Intel®Xeon®Silver 4114 CPU @ 2.20GHz（17年第三季度发布）的单核上，ECDSA性能与密钥长度2048位的公认RSA之间的总差是3.5倍。

让我们看一下在同一处理器上为ECDSA和RSA运行openssl -speed命令的结果。

在这里，我们可以找到对先前撰写的论文的确认，该论文关于签名的计算操作及其验证在ECC和RSA之间如何不同。 当前，与RSA相比，基于TLS 1.3的椭圆曲线加密技术在显着提高服务器性能的同时还提供了更高级别的保护。 这就是我们在Qrator Labs推荐并大力鼓励准备使用ECDSA证书的客户的主要原因。 在现代CPU上，支持ECDSA的性能提高了5倍。

如果您对（家庭或服务器）处理器如何处理密码计算感兴趣，请运行openssl speed命令。 -rsa ， -ecdsa和-eddsa允许您指定基准测试所需的算法。

未来（叠加）

具有讽刺意味的是，在编写此材料的过程中，Google宣布“实现量子优势” 。 这是否意味着我们已经处于危险之中，并且当前所取得的所有进展都不再能够确保保密？

不行

正如布鲁斯·施耐尔（Bruce Schneier）在IEEE安全和隐私通函的“外星人登陆后的密码学”一文中所写，量子计算机只能对具有公钥的非对称密码学真正造成严重的打击。 对称算法将保持不变。

但接下来，我们将请施耐尔先生本人发言：

还有另一种不需要量子计算机的情况。 虽然我们现在有几种数学理论是密码学中所使用的单面性的基础，但是这些理论的有效性的证明实际上是计算机科学中最大的开放性问题之一。 就像智能密码学家可以找到有助于破解特定算法的新技巧一样，我们可以想象外星人具有足够的数学理论来破解所有加密算法。 今天，这似乎很荒谬。 公钥密码术是一种数字理论，可能容易受到具有数学思想的外星人的攻击。 对称密码是如此非线性，创建和复杂化如此简单，以及加长密钥多么容易，这是未来无法想象的。 一个示例是AES变体，具有512位块和密钥大小以及128个回合。 如果数学与我们当前的理解并没有根本不同，那么这种算法将是安全的，直到计算机由物质以外的东西组成并且占据空间以外的东西为止。

但是，如果发生了无法想象的事情，那么仅基于信息理论的一次性密码记事本及其变体将使我们只剩下密码学。

布鲁斯·施耐尔（Bruce Schneier）完美地描述了除了实现错误之外，还可以发现现代加密技术的主要漏洞的领域。 如果某个地方有一群富裕的数学家，密码分析家和密码学家，以及致力于证明或驳斥某些特别复杂的数学问题（例如P？= NP）的计算机工程师，他们目前已经在这项活动中取得了一些进展-我们的位置很脆弱。 通过拒绝阴谋论，可以说在计算机科学，信息论和可计算性理论领域的这种进步很难被掩盖。 这样的事件本可以在“历史”的页面上，尤其是在“互联网历史”的教科书中输入其自己的创建者的姓名，这对于任何如此聪明的个人或团体都是无价之宝。 因此，类似的情况可能会被丢弃为不可能。

尚不清楚在未来的5年内是否会在量子计算上取得如此成功-并且已经存在适用于后量子世界的密码学原语：使用椭圆曲线的超奇异异构化的晶格，哈希函数，纠错码。 现在，安全专家仅在试验它们，但是毫无疑问，如果有必要，人类将找到一种方法来快速大规模部署新算法。

仍然需要补充的是，在未来十年中，基于椭圆曲线的密码学似乎非常适合大多数用户为其设定的目标和需求，从而提供安全性和高性能。