旋转,重新排列和降低预定的形状顺序,“俄罗斯方块打印机算法”使用“俄罗斯方块”机制生成任意位图。
算法说明
该算法将源图像的像素逐行转换为
Tetris场的平方,从下到上移动。 为了生成单个正方形,该算法组装了一个由矩形区域组成的结构,该矩形区域完全由其下方的一个正方形支撑。 矩形区域的组装完成后,将其线条清除,在其下方保留一个正方形。 这是此行为的三个示例。
如下所示,该算法还可以生成具有一种结构的多个正方形。
在构造行的过程中,以这种方式创建的所有正方形都必须基于某种东西。 在上面显示的图像中,生成的正方形位于运动场的地板上。 但是,如果任意线包含孔,则它将无法提供在其上方构建线所必需的支撑。 该算法通过在带孔的字符串顶部创建一个平坦平台来解决此问题。 在下面的动画中,建立在线条顶部的平台由一个红色正方形组成。 平台是一个临时结构,插入最后一个形状会将其删除。
下图所示的5个红色正方形所在的行位于3个红色正方形所在的行的顶部。 这是通过在底线顶部构建一个平坦平台来实现的。 该平台提供了生成5个红色正方形所需的支持。 最后,通过插入最后一个形状删除平台,然后将新行放置到位。 请注意,如果算法需要以相反的顺序生成线(在5个红色正方形的线上方3个红色正方形的线),则将不需要平台。
一平方模式
作为参考,我将给出7个tetramino(游戏作品)的名称。
本文中介绍的Tetris Printer Algorithm版本专门设计用于渲染旧视频游戏中的sprite。 这些游戏将图形打包为8×8的图块,并为每个像素分配了2个字节。 因此,子画面通常仅包含3种颜色以及透明区域,并且通常大小为16×16或16×32像素。
下面的动画显示了用于创建单个正方形的所有图案。 每个图案都使用可互换的四氨基J,T和L,在底部创建一个正方形。 该算法将此四氨基分配给精灵中存在的3种颜色之一。 其余的四氨基分配了任意颜色。 在整个游戏过程中,所有颜色保持不变。
由于三个四氨基的形状,不可能在前两列和后两列中用所有三种颜色创建一个正方形。 因此,用于渲染具有16个像素宽度的sprite的运动场的最小宽度为2 + 16 + 2 = 20平方。 但是,事实证明20太少了。
如下所示,单个底部正方形上方的区域不能仅由一条线组成,因为只有适合它的图形(丁米诺I)没有支撑。
用两条线,伸展整个比赛场地以便获得支持的唯一方法是使用tetramino S和Z。但是在这种情况下,顶行将保留孔。
底部正方形上方所需的最小行数为3,并且如上几次所示,存在这种模式。 20平方是放置16像素宽度的精灵所需的最小宽度。 但是20×3 +1 = 61,这个数字不能被4整除,这意味着它不能用四氨基建造。 但是,宽度21为21×3 +1 = 64,它可以由16个四氨基组成。 实际上,此宽度允许算法渲染精灵高达17个像素的宽度。
原始俄罗斯方块的运动场大小为10×20平方(比例为1:2)。 在此算法版本中,此比率得以保留-运动场的大小为21×42平方。
由于四氨基J,T和L在创建一个正方形时是可互换的,并且这些四氨基中的3个正方形参与在其上方创建线,因此有21-3 = 18个样式可用于创建一个正方形。 但是,由于镜像对称,实际上只有9条线。其中9条中的大多数都使用3条线。但是,彻底的计算机研究表明,这两种图形还需要更多。 下一个可能的选择是7行,因为21×7 + 1 = 148,需要37个四氨基。 如下图所示,存在这种模式。
多个正方形图案
用于创建多个正方形的图案限于由单个正方形的图案创建的相同三种颜色。 生成的正方形是由四氨基J,T和L创建的,它们各自在创建线上方的一条线上占据3个正方形。 单个图案可以创建的最大正方形数为21/3 =7。但是,对于宽度为16像素的子画面,最右边的四氨基不能创建正方形。 即使在精灵的宽度为17像素的情况下,它也可以创建仅一种颜色的正方形。 因此,很少使用从7个正方形开始创建的模式。
可以使用枚举的组合来确定用于创建任意数量的正方形的模式的数量。 考虑下面的模式,该模式代表三个正方形上方的一行。 三个相邻的白色方块的每个块表示四氨基的一部分; 创建的正方形未显示。
三个四氨基产生4个空隙。 可以将21-3×3 = 12个暗角正方形任意插入这些空隙中以形成特定的图案。 可以通过将这些黑色正方形放置在将单个白色正方形视为分隔线的线上来计算分配这些黑色正方形的方式数量。
因此,将任务简化为计算多项式系数的值。 查看这些白色正方形,您可以理解,这是选择15种方法中的3种方法的问题。
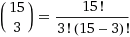
= 455。
在一般情况下,对于
n等于
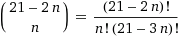
。 但是实际上,由于镜像对称,它们的数量只有后者的一半。 如果数量是奇数,然后除以2,我们将四舍五入到最接近的整数,以在其中包含一个理想对称的模式,该模式应该存在于该集合中,例如,对于455,如下所示。
将这个公式应用于7个四氨基,我们确认了一个明显的事实:只有一个模式可以创建7个正方形。
创建6个正方形的模式可以通过两种方式构建:两条实线(2×21 + 6 = 48)和六条实线(6×21 + 6 = 132),这需要12和33个四氨基。 上面的公式显示,有84种模式可创建6个正方形,但仅能用2条完整的线条构建其中的35种。 49个图案需要6线。 由于下面显示的对称图案,所以数字是奇数。
还值得注意的是,这里可以使用2条线,因为与创建一个需要四氨基S和Z的正方形的图案相反,在这些图案中使用了6个数字。
下表显示了每种图案类型创建的正方形数,完整线数,所使用的四氨基数量和图案数。
模式的例子。
平台类
在构造线之前,算法会检查其下方的线。 如果底行无法为其上方的所有方块提供支撑,则需要一个临时平台。 卸下平台后,一条新的线下降,并且由于原始Tetris中的重力实现方式,一些正方形仍然悬在空中。
下图显示了10种平台模式。 平台的构建从降低最后一条生成的线的一个正方形的顶部上的四氨基T开始。 其余的四氨基依赖于该第一个T。也就是说,如果先前生成的线包含至少1个正方形,例如下图中的红色正方形,我们可以在其上方创建一个平坦平台以生成下一行。
在构建平台的中间,完成并删除了底行,在其上方保留了三行。 在创建模式在平台顶部生成下一个精灵行之前,不会插入将删除这些行的最后一个四氨基J或L。 最后一个数字可防止在前两行中创建正方形。 但是,如上所述,由于此过程中使用的四氨基J,T和L的几何形状,用于创建正方形的图案仅限于17个内部列。
此外,在Tetramino T之上构建平台的19种可能方法中,上面仅显示了10种。
打包矩阵
如上所述,6个正方形创建模式的一个子集仅涉及清除两条线。 所有其他样式需要6行。 要了解为什么会这样,请考虑以下模式。
这些四氨基可与四氨基J和L互换,并且每个都向公共行添加3个相邻的正方形。 要完成的行由下面显示的矩阵表示。
现在整个事情是用四氨基填充空白空间。 从左侧开始,唯一的选择是使用tetramino I序列。
填充剩余空间的唯一方法是使用J和O或I和L。这两个选项如下所示。
不幸的是,上面显示的矩阵不支持四氨基O和L。 这个6平方的图案需要更大的矩阵。
在创建一个正方形的两种模式中也会出现类似的问题。 考虑下面的矩阵:
填充右边最底行的唯一方法是链接序列Z。
同样,在左下角获得3个空正方形的唯一方法是tetraminoS。
中线的S和Z之间有一个空的正方形,填充它的唯一方法是使用tetramino J,T或L,如下图所示。
插入这些形状中的任何一个都会分隔空格。 左侧的空白区域分别包含5、6和7个空白。 由于这些值均不能被4整除,因此无法继续。 该单个正方形图案需要更大的矩阵。
如下图所示,这同样适用于创建一个正方形的另一种模式。
用四氨基S和Z填充大部分底线后,中间的线之间没有空隙。
如下图所示,孔镶块划分出空白区域,左侧的空白区域分别包含9、10或11个正方形。 没有一个数字可以被4整除。
但是,打包矩阵并不是生成正方形图案的唯一方法。 例如,看看下面的4个正方形创建者。
以下是尝试将图案呈现为一组包装的丁胺酮的尝试。
跳过最后一个L,因为仅在完成和删除第三行之后才形成最后一个L的空间。
但是经过彻底的搜索,发现该技术不能为上述的单正方形图案提供仅使用3条线的功能。 此外,它不允许在两行中实现任何新的6平方的模式。 无需在打包矩阵之外查找剩余的模式,因为它们已经使用了最小量的四氨基。 并且将自己限制在打包矩阵中,我们将更快地找到所有必需的模式。
模式搜索
为了简化数据输出,“俄罗斯方块打印机算法”仅限于在运动场的顶部中心点创建四氨基,然后旋转,水平移动并降低它。 经过一段距离后,他再也不必水平移动图形了。 这种限制大大减少了搜索空间,因为它不允许在添加到矩阵的图形下形成间隙。 作为示例,让我们看下面的3个方阵。
如果我们将J放在矩阵的中心,如上所示,那么我们将得到2个空方格的间隙,无法用后续图形填充。 因此,搜索将不会遵循此路径。
由于不允许覆盖间隙,因此矩阵中的每一列都可以视为一堆实心正方形,并且这些堆叠的高度充分描述了整个矩阵的内容。 无论行数如何,具有21个元素的一维整数数组都足以描述二维矩阵。
当图形落入矩阵中时,相应列的堆栈高度会增加。 为了加速这一过程,所有四胺都需要预先分析。 有19个四米诺米级转弯,搜索将它们视为一个唯一的图形。
图像左上角的Tetramino J占据3列。 当降低到矩阵上时,3个相邻堆栈的高度分别增加1、1、2个正方形。 但是在降低图形之前,图形的下部轮廓必须对应于各个堆叠的上部轮廓。 如果这个J躺在运动场的地板上,则在这些列的每一列下应该有1个,1个和0个空正方形的间隙。 由于禁止间隙,因此3叠的相对高度必须完全匹配该图案。
缺少间隙的另一个结果是,当图形落入矩阵时,行从下至上填充。 在矩阵中部之前或同时未完成其下所有行的情况下,无法填充行。 在填充矩阵的过程中,其下边界实际上向上移动。 因此,矩阵列堆栈只有在其高度减去已完成的行数大于0时才能提供支持。将形状添加到矩阵时,至少一个相应的列必须提供支持。
搜索存储第二个一维数组,该数组包含每行中已填充正方形的数量。 上面的J在相应的线3和1中包含一个正方形。 将其插入矩阵时,这些值将添加到数组的相应元素中。 已完成的行数是值为21的元素数。
如上一节所述,如果添加的图将矩阵除,则结果区域的大小应除以4。例如,在下图中,添加I创建2个区域,每个区域包含46个空正方形。 由于46不能被4整除,因此不再有任何方法可以填充矩阵的其余部分。
当堆栈的高度等于矩阵的高度时,出现分离。 通过增加相应堆栈的高度插入图形后,可以通过扫描高度数组并将每个堆栈中剩余的空间相加来确定空白区域的所有划分区域的尺寸。 检测到拆分后,将检查并重置此编号。
用于生成所有模式的搜索使用随机增量构造,这是一种以随机顺序系统地检查所有组合的回溯算法。 通过随机插入形状来递增构造溶液,使其像晶体一样生长。 随机性提供了包含断面的不规则性,这些断面用作后续添加形状的基础。 大多数矩阵都非常快速地随机打包,并且当空白空间变得稀缺时,回溯就起作用了。
在执行搜索之前,执行将图形添加到矩阵的371种方式的随机排列。 搜索功能的伪代码如下所示。
private Result search(Matrix matrix, int remaining) { if (remaining == 0) { return SOLUTION } attempts := attempts + 1 if (attempts >= MAX_ATTEMPTS) { return TIMEOUT } if ( S Z) { S Z if ( ) { Result result := search(matrix, remaining - 1) if (result == SOLUTION) { return SOLUTION } if (result == TIMEOUT) { return TIMEOUT } } } for( , ) { if ( ) { Result result := search(matrix, remaining - 1) if (result == SOLUTION) { return SOLUTION } if (result == TIMEOUT) { return TIMEOUT } } } return NO_SOLUTION }
传递给搜索函数的原始矩阵为空,但最下面一行包含3个相邻正方形的块除外。 它与需要添加的剩余图形数一起发送。 如果
remaining为0,则矩阵包含解,函数返回。 每个递归调用都会增加尝试的全局尝试
attempts 。 如果它超过
MAX_ATTEMPTS (其值为1000),那么搜索将再次开始。
如果空间允许,第三个
if尝试将四氨基S或Z添加到矩阵的底部。 这样做的意思是避免出现如下所示的情况,即当算法花时间填充矩阵的一部分时,由于缺乏支持而无法填充其余部分。
感谢
if它迅速形成了一个构建平台:
尝试将图形添加到矩阵,需要进行上述检查。 给定已完成的行,该算法将检查图形是否将得到支持。 它还检查是否将其除以因插入形状而创建的每个独立空白空间的大小4。
影像转换
俄罗斯方块打印机算法将位图的每一行转换为一系列遍。 从左向右移动,每个段落以“贪婪”的方式将四氨基J,T和L插入到放置它们的位置。 例如,下图显示了位图的16个像素行。
下图显示了覆盖这16个像素所需的5次通过。
算法尝试插入的形状顺序由像素的颜色确定。 为了使形状不重叠,使用了布尔值的一维数组。 要插入图形,数组中必须存在3个零元素。 成功插入图3后,相应的数组元素取值为1。
为了跟踪多遍之间的完成像素,使用了第二个一维布尔值数组。 当每个项目为1时,该行将完成。
在每次扫描结束时,图像转换器都会在表格中搜索所有用于创建一个或多个正方形的图案。 在输出中,它传递了相应的图案,底部插入了四氨基J,T和L,例如,上面显示的第一遍显示为以下用于创建5个正方形的图案:
即时搜寻
上一节中描述的图像转换器非常快,因为它使用包含所有用于创建正方形的图案的常量表,并且不会实时搜索它们。 但是,实时搜索可以使用表中未包含的模式,因此可以大大减少生成图像所需的四氨基酚数量。 他使用先前段落中创建的正方形,将它们用作辅助支撑。 例如,如上所述,以下用于创建一个正方形的模式需要7条实线。
但是,在下图的左下角的上一个段落中创建的一个红色正方形提供了额外的支持,从而将实线的数量减少到了3。
此外,通过翻转四氨基J,T或L,实时搜索可以覆盖3个相邻的相同颜色的像素。
实际上,它可以结合反向和反向四氨基,一次通过覆盖大量像素。 例如,可以将覆盖16个像素的上述5次通过减少为以下所示的单次通过。
为了获得此图案,图像转换器首先急切包装上翘的四氨基J,T和L。
然后,他急切地尝试添加未翻转的版本,在这种情况下,他设法添加了另一个J。
原则上,在此过程中也可以使用预先计算的查找表,但是这种表的绝对大小使其在实践中不适用。
在此示例中,将要创建的行上方的行中的8个正方形添加到空矩阵的底部行。 对于21平方英尺宽的运动场上的
n个正方形,矩阵
h的高度是最小的正整数,因此
21h-n可被4整除。在这种情况下,需要高度为4的矩阵。
实时搜索的工作方式与上述搜索算法完全相同,但有较小的改进。 和以前一样,矩阵列堆栈仅在列高减去已完成的行数大于零时才提供支持。 当差异为零时,列堆栈不应提供支持。 但是,在此版本中,如果它等于零,它将检查由先前遍次生成的所创建行中的平方。 也就是说,矩阵底部行下方的行中的任何正方形都为空列提供支持。
另外,由于搜索是实时执行的,因此使其详尽无遗。 如果在给定的尝试次数后仍未找到解决方案,则他将在矩阵顶部再添加4行,然后再次尝试。 此后,如果在给定的尝试次数之后他仍然找不到解决方案,那么在当前段落中,他将返回本文前面部分介绍的带有预先计算的搜索表和图像转换的方法。
列印
要进行打印,您必须遵循Tetris运动场上图像转换器显示的说明。 打印机以标准方向在运动场的顶部中心点创建特定的丁胺。 然后打印机旋转它,水平移动它并放下它。 视频中显示了此过程:
源代码
Java 7项目的源代码在
此处 。
包
search.precomputed和
search.realtime中提供了用于预先准备的表和实时的搜索算法。 他们使用位于
search包中的一些通用类。 预先计算的搜索结果以文本文件序列的
patterns存储在
patterns包中。 文本文件将打包的矩阵以ASCII字符存储,以
A开头
A 例如,
emitters1.txt (用于创建一个正方形的一组模式)中的前三个矩阵如下所示:
如文章中反复所述,上述矩阵中的3个相邻的
A符号可以用四氨基J,T或L代替。符号
B ,
C ,
D等表示您需要创建的四氨基序列。
imageconverter.ImageConverter类包含
main方法,该方法接收一个命令行参数:图像精灵文件的名称。 图片不能大于17×32像素,并且不能包含3种以上的不透明颜色。 所有其他像素必须是透明的。
有趣的是,在旧的视频游戏中,开发人员经常使用背景来获得额外的颜色。 例如,Bubble泡泡的气泡的学生和嘴巴,Donkey Kong的Donkey Kong的学生和Pakman小姐的mole鼠的眉毛。 吃豆人实际上是透明的。 黑色来自纯色背景。
俄罗斯方块运动场的背景可以类似的方式使用。
ImageConverter输出如下所示:
第一行中的3个十六进制值是从子画面图像文件中提取的3种不透明颜色。 它们对应于四氨基J,T和L的颜色。其他四氨基的颜色不影响图像。 其余的块是在游戏场上执行的打包模式(对于
Z之后至
a 的字符 a请参见
ASCII字符表 )。 突出显示的黄色块构成了平台。 第一块添加平台,第二块删除平台。
printer.Printer类接收这种格式的文本文件,并通过播放Tetris生成图像文件。
用于生成类似于
俄罗斯方块的
NES版本的视频的打印机算法在文本文件的每个块中定义了每种丁胺醇类型。 然后它以相反的顺序从起点和初始方向移动到文件中指示的图形的旋转角度和下降坐标。 注意:由于数字下降的速度非常快,在真正的NES版本的俄罗斯方块中不可能超过30级。 假定打印机足够快地将其所有命令传输到运动场。 为了弥补这一点。
要重新生成特征码文件,请使用
search.precomputed.PatternSearcher 。 可以通过更改源代码文件开头的常量来自定义。
public static final int MATRIX_WIDTH = 21; public static final int MATRIX_HEIGHT = 4; public static final int EMITTED_SQUARES = 4; public static final int RANDOM_SETS = 100000; public static final int MAX_ATTEMPTS = 1000;
RANDOM_SETS是将图形添加到矩阵的371种方式的随机排列数。 设置为
100000 ,在启动时初始化排列需要花费几秒钟的时间。 另外,它们的存储需要超过1 GB的内存。
MAX_ATTEMPTS控制搜索的执行时间。 相对较小的值
1000可以使搜索快速丢弃无法很好地展现自己的随机起点。 但是,为了证明对于特定的矩阵大小和创建的平方数没有解决方案,有必要充分探索整个搜索空间。 为此,您可以将
MAX_ATTEMPTS设置为
Integer.MAX_VALUE 。
在图像转换器使用的
search.realtime.RealtimeSearcher可以找到类似的常量。 如上所述,较大的
RANDOM_SETS值需要增加最大内存,并导致启动时间更长。
MAX_RETRIES控制尝试次数,之后实时搜索放弃并返回带有预先计算表的搜索。
请记住,两种搜索算法都使用100%的CPU,从而创建了许多并行线程,这些线程的大小等于可用处理器的数量。