Equal Citizens的科学家兼首席财务官Phoebe Wong 谈到了认知科学中的文化冲突。 Elena Kuzmina将文章翻译成俄语。
几年前,我观看了有关自然语言处理的讨论。 Google的研究主管
彼得·诺维格 (
Peter Norvig)是“现代语言学之父”
诺姆·乔姆斯基 (
Noam Chomsky)讲话。
乔姆斯基思考自然语言处理领域朝着哪个方向发展,并
说 :
假设某人即将清算物理部门,并希望按规则进行。 根据规则,您可以拍摄无数关于世界上正在发生的事情的视频,将这些千兆字节的数据馈送到最大,最快的计算机上,并进行复杂的统计分析-嗯,您知道:贝叶斯“来回” *-您将获得关于窗外将会发生什么。 实际上,您将获得比物理学院给出的更好的预测。 好吧,如果成功是由您与混乱的原始数据的接近程度决定的,那么这样做比物理学家的方法更好:无需在理想的表面上进行思想实验等。 但是您将不会获得科学一直追求的那种理解。 您得到的只是对现实情况的粗略了解。
*来自贝叶斯概率-概率概念的一种解释,其中概率被解释为合理的期望,而不是某种现象的发生频率或趋势,代表对个人信念或知识状态的定量评估。 人工智能研究人员在机器学习中使用贝叶斯统计数据来帮助计算机识别模式并基于它们做出决策。
乔姆斯基反复强调这个想法:今天在处理自然语言上的成功,即预测的准确性,不是一门科学。 据他介绍,将大量文本输入“复杂的机器”中只是近似原始数据或收集昆虫,而不会真正理解该语言。
根据乔姆斯基的说法,科学的主要目标是发现有关系统实际运行方式的解释性原理,而实现这一目标的正确方法是允许理论指导数据。 有必要通过精心设计的实验从“不相关的包含物”中抽象出来,研究系统的基本性质,也就是说,与伽利略时代以来科学界所接受的方式相同。
用他的话说:
一个简单的处理原始混沌数据的尝试不可能将您引向任何地方,就像伽利略不会将您引向任何地方一样。
随后,诺维希(Norwig)在一篇
长文中回应了乔姆斯基的说法。 Norvig指出,在语言处理应用程序的几乎所有领域中:搜索引擎,语音识别,机器翻译和回答问题,训练有素的概率模型盛行,因为它们比基于理论或逻辑规则的旧工具要好得多。 他说,乔姆斯基在科学上取得成功的标准-强调“为什么”问题和轻描淡写“如何”的重要性-是错误的。
他引用理查德·费曼(Richard Feynman)的话证实了他的立场:“物理学可以没有证据而发展,但是我们不能没有事实而发展。” 诺威格回忆说,概率模型每年产生数万亿美元,而乔姆斯基理论的后代则以不到10亿美元的收入为由,理由是乔姆斯基在亚马逊上出售的书籍。
诺威格(Norwig)认为乔姆斯基(Chomsky)对“贝叶斯来回”的蔑视是由于莱奥·布雷曼(Leo Breiman)所描述
的统计建模中
两种文化的分裂:
- 假设自然是黑盒子的数据建模文化 ,其中变量是随机连接的。 建模专家的工作是确定最适合其基础的关联的模型。
- 算法建模的文化意味着黑匣子中的关联过于复杂,无法使用简单的模型进行描述。 模型开发人员的工作是选择一种使用输入变量对结果进行最佳评估的算法,而不期望可以理解黑匣子内部变量的真正基本关联。
诺维格(Norvig)认为,乔姆斯基(Chomsky)与其说是概率模型,不如说是对立,而是不接受带有“四十亿个参数”的算法模型:它们不容易解释,因此对于解决“为什么”的问题毫无用处。
Norwig和Breiman属于另一个阵营-他们认为语言之类的系统过于复杂,随机且任意,无法用一小部分参数表示。 从困难中抽象出来就像是将一个神秘的工具调整到实际上不存在的某个永久区域,因此,语言是什么以及它如何工作的问题被忽略了。
诺维格(Norwig)在
另一篇文章中重申了他的论点,他认为我们应该停止行动,就像我们的目标是创造极其优雅的理论一样。 相反,您需要接受复杂性并使用我们最好的盟友-不合理的数据效率。 他指出,在语音识别,机器翻译以及几乎所有针对Web数据的机器学习应用程序中,基于n-gram模型或基于数百万个特定功能的线性分类器之类的简单模型要比复杂模型更好。谁试图发现一般规则。
在这次讨论中,最吸引我的不是乔姆斯基和诺维格的不同意,而是他们团结在一起的内容。 他们同意,使用统计学习方法对海量数据进行分析而又不了解变量的情况,比起尝试对变量之间如何相互关联进行建模的理论方法,可以提供更好的预测。
我不是唯一对此感到困惑的人:与我交谈过的许多具有数学背景的人也发现这是矛盾的。 最适合建模基本结构关系的方法是否也具有最大的预测能力? 或者我们如何在不知道所有工作原理的情况下准确地预测某事?
预测因果关系
即使在经济学和其他社会科学等学术领域,预测能力和解释能力的概念也经常相互结合。
具有高解释能力的模型通常被认为具有高度预测性。 但是,构建最佳预测模型的方法与构建最佳解释模型的方法完全不同,建模决策通常会导致两个目标之间的折衷。 在
统计学习简介 (ISL)中说明了方法上的差异。
预测建模
预测模型的基本原理相对简单:使用一组易于获得的输入数据X评估Y。如果误差X平均为零,则可以使用以下方法预测Y:
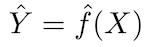
其中ƒ是X提供的有关Y的系统信息,对于给定的X得出Ŷ(对Y的预测)。如果确切的函数形式可以预测Y,则通常并不重要,而ƒ被视为“黑匣子”。
这种类型的模型的精度可以分解为两个部分:可减少的误差和致命的误差:
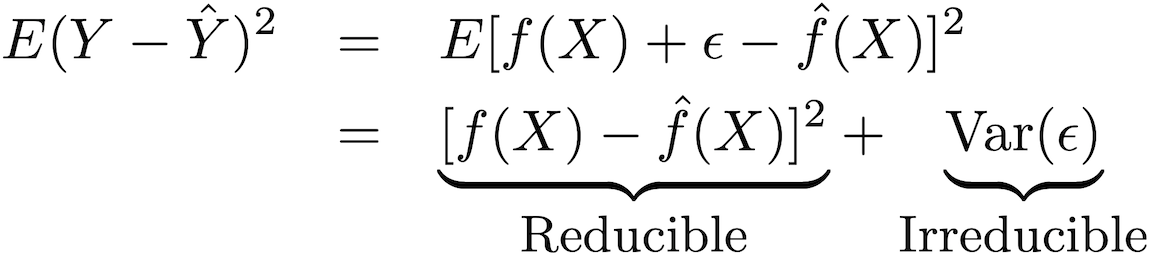
为了提高预测模型的准确性,有必要使用最合适的统计训练方法进行估计以最小化可减少的误差,以便评估ƒ。
输出建模
如果目标是了解X和Y之间的关系(Y如何随X改变),则不能将ƒ视为“黑匣子”。 因为我们不知道函数形式ƒ就无法确定X对Y的影响。
几乎总是在对结论建模时,使用参数方法来估计ƒ。 参数标准是指此方法如何通过采用参数形式ƒ和通过建议的参数评估ƒ来简化ƒ的估计。 此方法有两个主要步骤:
1.假设功能形式ƒ。 最常见的假设是ƒ在X中是线性的:
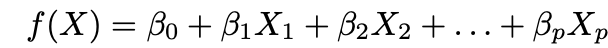
2.使用数据拟合模型,即找到参数β₀,β₁,...,βp的值,以便:
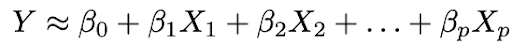
最常见的模型拟合方法是最小二乘(OLS)方法。
灵活性和可解释性之间的权衡
您可能已经想知道:我们如何知道ƒ是线性的? 实际上,我们将不知道,因为真实形式ƒ是未知的。 而且,如果所选模型与实际ƒ相距太远,则我们的估计将有偏差。 那么,为什么我们首先要做出这样的假设? 因为模型灵活性和可解释性之间存在内在的折衷。
灵活性是指模型可以创建以适合许多不同的可能功能形式的形式范围。 因此,模型越灵活,可以创建的拟合越好,从而提高了预测的准确性。 但是,更灵活的模型更加复杂,需要更多的参数来拟合,并且估计值通常变得过于复杂,以至于无法解释任何单个预测变量和预后因素的关联。
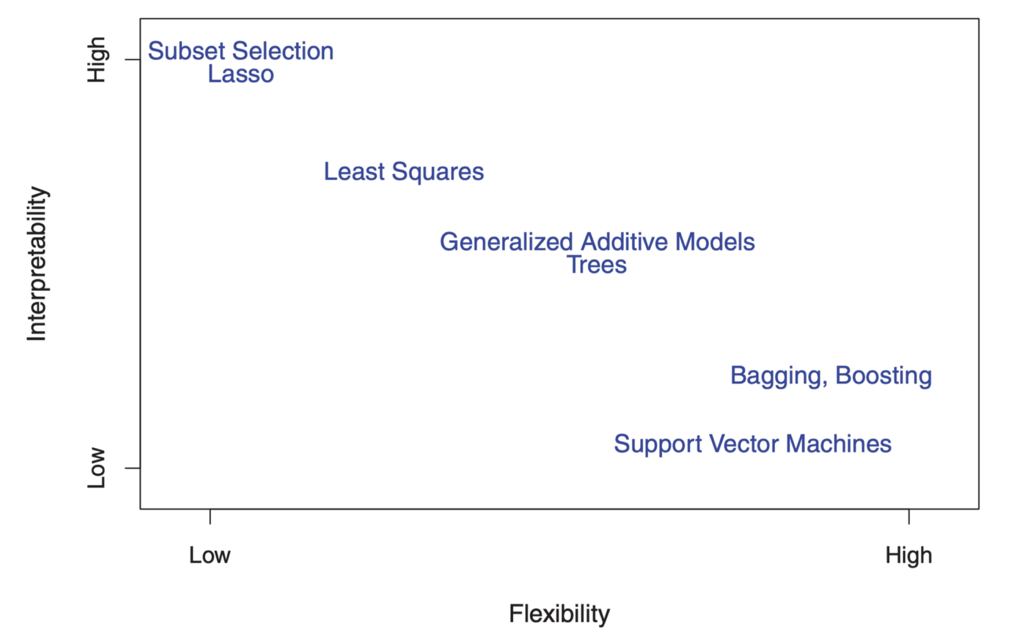
另一方面,即使线性模型不能很好地执行准确的预测,线性模型中的参数也相对简单易懂。 这是ISL中的一个很棒的图表,它说明了各种统计培训模型中的这种权衡:
”
”
如您所见,具有更好的预测准确性的更灵活的机器学习模型(例如支持向量法和增强方法)同时具有较低的可解释性。 推理建模还拒绝解释模型的预测准确性,因此对函数形式f做出了可靠的假设。
因果识别和反事实推理
但请稍等! 即使您使用具有良好拟合的良好解释模型,也仍然不能将这些统计数据用作因果关系的单独证据。 这是由于陈旧而陈旧的陈词滥调“关联不是因果关系”。
这是一个
很好的例子 :假设您有关于一百个旗杆的长度,其阴影的长度和太阳的位置的数据。 您知道阴影的长度由极点的长度和太阳的位置确定,但是即使将极点的长度设置为因变量而将阴影的长度设置为自变量,您的模型仍将拟合统计上显着的系数,依此类推。
这就是为什么因果关系不能仅通过统计模型建立并且需要基础知识的原因-所谓的因果关系应通过对关系的一些初步理论理解来证明。 因此,因果关系的数据分析和统计建模通常主要基于理论模型。
即使您有充分的理论根据说X导致Y,也常常很难确定因果关系。 这是因为评估因果关系涉及确定在没有发生X的反作用世界中会发生什么,这在定义上是不可观察的。
这是
另一个很好的例子 :假设您想确定维生素C对健康的影响。 您是否有关于某人是否正在服用维生素的数据(如果正在服用,则为X = 1;如果不服用,则为0-不服用),以及某些二元健康结果(如果他们健康,则为Y = 1; 0-不健康)看起来像这样:
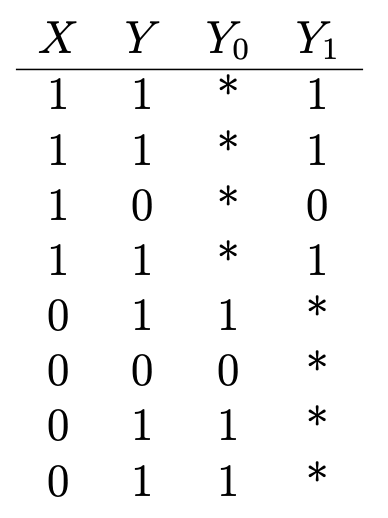
Y₁是服用维生素C的人的健康结果,Y₀是不服用维生素C的人的健康结果。 为了确定维生素C对健康的影响,我们评估了平均治疗效果:
但是,要做到这一点,重要的是要知道如果不服用任何维生素C,那么服用维生素C的健康后果将是什么,反之亦然(或E(Y₀| X = 1)和E(Y₁| X)。 X = 0)),在表格中以星号表示,代表未观察到的反事实结果。 没有此输入,就无法顺序评估平均治疗效果。
现在想象一下,已经健康的人通常会尝试服用维生素C,但已经不健康的人却不会。 在这种情况下,即使维生素C根本不影响健康,评估也将显示出强大的治愈效果。 在这里,以前的健康状况称为混合因素,既影响维生素C的摄入量又影响健康(X和Y),从而导致估计值失真。 获得一致的θ分数的最安全方法是通过实验将治疗随机化,以使X不依赖于Y。
如果随机开出处方,则平均而言,未接受药物治疗的组的结果将成为客观指标,表明接受药物治疗的组的反事实结果,并确保没有扭曲因素。 A / B测试就是基于这种理解。
但是随机试验并非总是可行的(如果要研究吸烟或吃太多巧克力饼干对健康的影响,这是伦理学),在这种情况下,应从通常采用非随机治疗的观察结果中评估因果关系。
有
许多统计方法可以识别非实验条件下的因果关系。 他们通过建立反事实结果或在观察数据中建模随机治疗处方来实现此目的。
不难想象,这些类型的分析结果通常不是很可靠或无法再现。 甚至更重要的是:这些方法上的障碍并不是要提高模型预测的准确性,而是要通过逻辑和统计结论的结合来提供因果关系的证据。
衡量因果关系模型的成功率要容易得多。 尽管对于预后模型有标准的绩效指标,但是评估因果模型的相对成功要困难得多。 但是,如果很难找到因果关系,那并不意味着我们应该停止尝试。
这里的要点是,预测模型和因果模型具有完全不同的目的,并且需要完全不同的数据和统计建模过程,而且我们经常必须同时执行这两个过程。
电影业的一个例子表明:制片厂使用预测模型来预测票房收入,预测电影发行的财务结果,评估其电影投资组合的财务风险和获利能力等。但是,预测模型不会使我们更了解电影市场的结构和动态,也不会帮助我们制作电影。投资决策,因为在电影制作过程的较早阶段(通常是发行日期之前的几年),在做出投资决策时, 结果很高。
因此,大大降低了早期基于初始数据的预测模型的准确性。 当大多数制作决策都已经制定并且预测不再特别可行且相关时,预测模型就接近电影发行的开始日期。 另一方面,因果关系的建模使制片厂能够发现各种制作特征如何影响电影制作早期阶段的潜在收入,因此对于告知其制作策略至关重要。
对预测的关注增加:乔姆斯基是对的吗?
不难理解乔姆斯基为何会感到沮丧:预后模型在科学界和行业中占主导地位。
对学术预印本的
文本分析表明,定量研究发展最快的领域越来越重视预测。 例如,人工智能领域中提及“预测”的文章数量增加了一倍以上,而有关结论的文章自2013年以来减少了一半。
数据科学课程在很大程度上忽略了因果关系。 业务中的数据科学主要关注预测模型。 著名的现场竞赛(例如Kaggle和Netflix奖)基于改进的预测绩效指标。
另一方面,仍然有很多领域对经验预测没有给予足够的重视,它们可以从机器学习和预测建模领域取得的成就中受益。 但是,将当前的状况描述为“ Chomsky团队”和“ Norvig团队”之间的文化战争是不正确的:没有理由只选择一种选择,因为两种文化之间有很多相互充实的机会。 为了使机器学习模型更容易理解,已经做了很多工作。 例如,斯坦福大学的
Susan Ati在因果关系方法中使用了机器学习方法。
最后,回顾一下
裘德·珀尔(Jude Pearl)的
作品 。 Pearl于1980年代领导了一项有关人工智能的研究项目,该项目使机器可以使用贝叶斯网络进行概率推理。 但是,自那以后,他成为最大的批评家,认为人工智能仅关注概率关联和相关性如何成为成就的障碍。
Pearl赞同乔姆斯基的观点,
认为深度学习的所有令人印象深刻的成就都归结为数据曲线的拟合。 , ( ), 30 . , — « ».
, - , , — , , .
, - , , .
在他的一篇文章中,他声称:人类的大多数知识都是围绕因果关系而不是概率关系来组织的,并且计算概率的语法不足以理解这些关系。因此,我认为自己只是贝叶斯的一半。
似乎只有当我们有更多的零碎东西时,数据科学才会受益。