哈Ha！ 我向您介绍Joos Korstanje撰写的文章
“假设检验和P值的直观解释”的翻译。
几年前，我为一家果蔬配送公司做了第一份自由统计工作。 每天二十四小时，农民收到的产品在送到超市之前都要经过质量控制部门。 产品的选择是由该部门的员工随机进行的。
他们在年度报告中注意到，今年的质量要比过去的质量低：相差1到10左右仅相差了半个百分点。
然后他们邀请了我。 我不得不回答这个问题：
这些0.5点是否有显着差异？如果您不知道统计信息，那么这个问题对您来说似乎很奇怪。 但请放心：本文的目的是向您展示如何使用假设检验（也称为统计推断）回答这个问题。
数字游戏：一个苹果的贡献
想象一下，您正在使用一个非常大的装有苹果的盒子中随机选择一个苹果来检查一个苹果的好坏。 在下图中，我们看到了样本量对测量的真实影响：一个苹果对小样本的影响非常显着，并且随着样本量的增加，影响越来越小。
一个苹果的贡献取决于样本量。了解样本量的影响是了解假设检验的第一个基础。 我们可以开始争辩说，两个苹果上的0.5就像一个苹果的差，很小。 但是，对于100个苹果，0.5等于50个苹果的差额：差异非常大！
对于小样本，0.5点是一个很小的差异，但是对于大样本0.5，这是一个很大的差异。样本应多大：假设检验和答案的重要性
有几种方法可以回答这个问题，但是在本文中，我将深入探讨统计推断或假设检验。
假设检验是一系列统计方法，用于了解如何观察对象的采样可用于接受或拒绝预定义的假设。 假设检验用于解决许多问题，主要是在科学研究中，并且是在线营销的一种重要方法（A \ B检验）。
数学家以一种确定真相的程序来开发假设检验。
假设检验允许您仅检验假设，而不能发展假设。从装有100个苹果的盒子（我们称其为人口）中，我们抽取了8个苹果的样本。 今年，在8个苹果中，有5个腐烂（62％），而在去年的样本中，有8个苹果中，只有4个是腐烂（50％）。 我们要使用假设检验来确定今年烂苹果的百分比是否大于去年。
假设检验是测量总体的一种数学替代方法。 通过这些计算，我们可以将小样本的测量结果推广到大样本人群。 因此，我们减少了工作量。
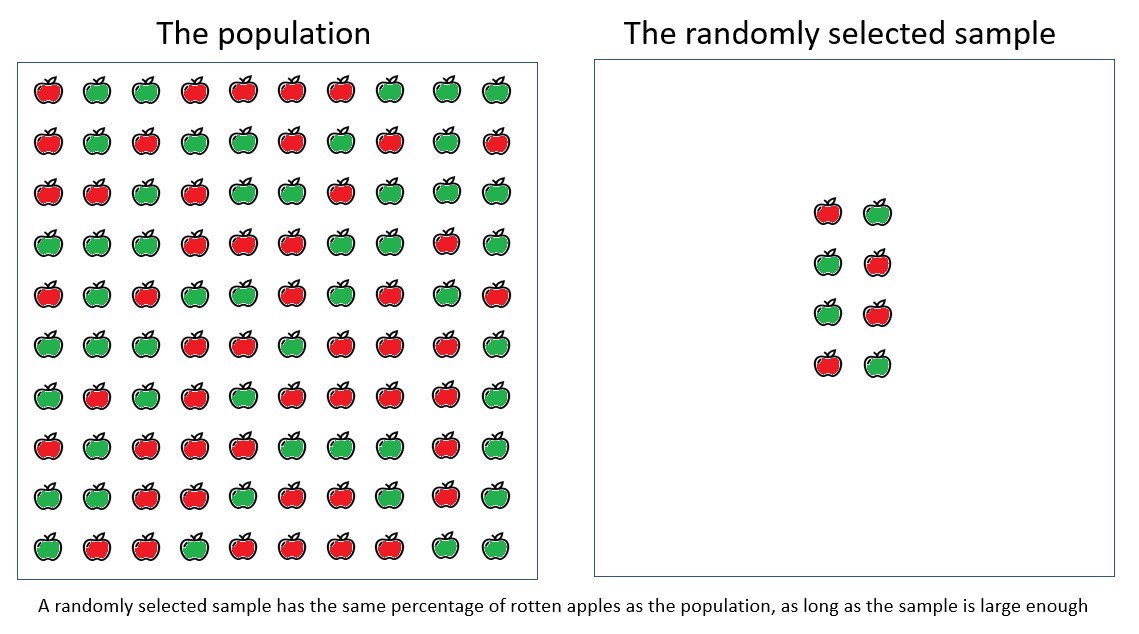
只要收集的样本足够大，则随机选择的样本的烂苹果百分比与总人口相同。
数学家们提出了一种基于样本向一般人群推广结论的方法。
该方法从明确研究假设的表述开始。 不幸的是，数学只有在我们已经知道要测试什么的情况下才起作用。
我们的示例的主要假设是：
今年，烂苹果在总人口中所占的比例比过去更高。实际假设检验
假设检验的数学形式在样本的测量结果与观察次数之间形成平衡。 结果是一个p值。这些计算通过使用分布进行：对于几乎每种想象的情况，都得出了描述预期结果的数学定律。
对于是/否问题，例如我们的烂苹果（烂/不烂）问题，适用抛硬币法。 这是数学定律的最简单示例：50％的尾巴，50％的鹰头。
它也可以非常简单地表示为标准数学分布，它告诉我们有关观测概率的信息。 例如，在10次硬币翻转中掉了7头鹰。 这称为二项分布，可以表示如下：
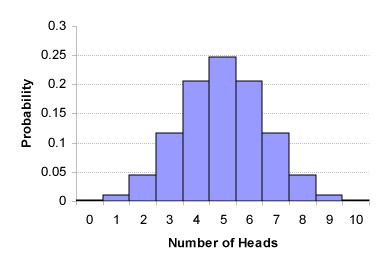10次硬币翻转的二项分布。在本文中，我将远离硬数学，但重要的是要知道我们可以使用数学公式来评估观察到的百分比是否与预期百分比相差甚远。
在本文的结尾，我将为您提供各种情况下常用的假设检验公式的列表，然后，我将解释如何使用它们。 但是首先，我将解释假设检验的解释。
假设检验结果：p值
除假设检验外，观察值与样本量之间也存在数学平衡。 在计算结束时，每个现有的假设检验选项都将产生一个标准化分数，即使数学并不完全相同，您也可以通过该分数比较结果。
P值是制定假设检验结果并将其用于任何其他检验的标准方法。
P值是一个介于0和1之间的数字，它告诉我们样本的观察值与假设之间的差异是否存在很大差异。 参考值为0.05。
如果p值小于0.05，则差异具有统计学意义。
如果p值大于0.05，则差异在统计上并不显着。
范例1：
我们进行了10次硬币翻转。
我们的假设：我们期望有5条尾巴。
我们的观察结果：我们有6条尾巴。
p值的计算得出0.518，大于0.05。
我们的结论是：差异没有统计学意义。
我们的解释：结果与假设一致。
范例2：
我们掷了10张硬币
我们的假设：我们期望有5条尾巴。
我们的结果是：我们有10条尾巴。
我们的p值为0.0，小于0.05。
我们的结论：差异具有统计意义
我们的解释：结果与假设不一致。
范例3：
我们检查了10个苹果。
我们的假设：我们希望有一个烂苹果。
我们的结果：我们得到了1个烂苹果。
我们的p值为1.0，大于0.05。
我们的结论：差异在统计上不显着
我们的解释：结果与假设一致。
范例4：
我们检查了10个苹果。
我们的假设：我们希望有一个烂苹果。
我们的结果是：我们有5个烂苹果。
我们的p值为0.0114，小于0.05。
我们的结论：差异具有统计意义
我们的解释：结果与假设不一致。
结论
在本文中，我对统计错误或假设检验的一般结构进行了直观的解释。 我希望现在您能更好地了解假设检验，以及它如何对您有用。
我没有深入研究数学证明和具体细节。 下表列出了我建议进一步研究的最常见的假设检验列表。
某些假设检验的替代假设列表。
希望本文对您有所帮助，并祝您在假设检验的进一步研究中好运。