双素假设是数学中最重要,最复杂的问题之一。 两位数学家为小型数值系统解决了该问题的并行版本。

9月7日,两位数学家
发表了关于数学中最著名的开放问题之一的版本的
证明 。 这一结果为
孪生素数假设的研究开辟了一条新的前沿,这一假设困扰着数学家一百多年,并且与算术的一些最深刻的特性有关。
牛津大学的数学家
詹姆斯·梅纳德 (
James Maynard)表示:“我们已经滑行了很长时间,我们已经没有足够的想法来完成这项任务了,所以任何人都有新想法很自然。”
孪生素数假设适用于相差2的素数对。孪生数为5和7,以及17和19。该假设指出,自然数中有无限数量的此类对。 在过去的十年中,数学家取得了长足的进步,但距离完整的解决方案还差得很远。
新证据的作者,来自哥伦比亚大学的
Will Savin和位于麦迪逊的威斯康星大学的
Mark Shusterman证明了一个较小但仍引人注目的数学世界的假设。 他们证明了它在只有几个数字的有限数值系统中的有效性。
这样的数字系统称为“有限域”。 尽管它们很小,但它们保留了无数整数固有的许多数学特性。 数学家正在尝试寻找有限域中算术问题的答案,并希望将这些结果转换为所有整数。
梅纳德说:“尽管有些天真,但最终的梦想是,对有限域的性质有一个很好的了解可以揭示整数世界。”
除了证明双素数的假设外,Savin和Shusterman还发现了有关小数值系统中素数行为的更令人惊讶的结果。 他们证明了孪生素数出现在小间隔的确切频率-这个结果使得可以非常精确地控制孪生素数的现象。 数学家梦想着用普通数字获得相似的结果。 他们探索新的证据以寻找适用于数字线上质数的想法。
一种新的素数
对孪生素数假设的最著名的预测是存在数量之差为2的无数对数。但是,这种说法更为笼统。 它说有无数个素数相差4(例如3和7),14(293和307)或您指定的任何数量。
阿方斯·德波利尼亚克(Alfons de Polignac)在1849年以现代形式
做出了这一假设 。 在接下来的160年中,数学家的进步并不大。 但是,在2013年,冰破裂了,或至少严重破裂了。 那年,
张伊森证明了无限数量的素数对的存在,相差不超过7,000万,第二年,包括Maynard和
Terry Tao在内的其他数学家就大大缩小了这一差距。 当前记录证明存在数量不限的互不超过246个素数对。
然而,在那之后,进展消退了。 数学家理解需要一个全新的想法来完全解决这个问题。 有限数系统是寻找这个想法的好地方。
要构建有限域,首先需要从自然数中提取数字的有限子集。 例如,您可以采用前五个数字(或任何素数)。 与其像往常一样在数字行上表示数字,不如想象一下以拨号盘形式出现的新数字系统。
正如您可能已经猜到的,算术开始在狭窄的空间中起作用。 在由五个元素组成的有限数值系统中,4 + 3将是什么? 我们从4开始,顺时针计数三个除法,然后得出2。减法,乘法和除法的工作方式相似。

但是只有一个陷阱。 在有限域中,素数的通常定义没有意义。 在最后一个字段上,任何数字除以其他任何数字。 例如,7通常不能被3整除。但是在五个元素的最后一个字段中,它可以被整除。 这是因为在最后一个字段中,数字7等于数字12-它们都以表盘的2标记结尾。 因此,将7除以3将得到与12除以3相同的结果,而将12除以3将得到4。
因此,有限域双素数的假设指的是简单多项式-例如x
2 +1的数学表达式。
例如,假设您的最终字段包含数字1、2和3。这些数字将是此有限字段中多项式的系数,而“简单”多项式将是不能分解为多项式因数的多项式。 因此,x
2 + x + 2将很简单,因为它无法分解,但x 2-1不会:这是(x + 1)和(x-1)的乘积。
定义了简单多项式之后,自然会问一个关于简单孪生多项式的问题-简单对且相差一个固定值的多项式对。 例如,多项式x
2 + x + 2很简单,就像x
2 + 2x + 2一样。它们相差x。
有限域的简单孪生多项式的假设表明存在无限多的简单孪生多项式对,它们之间的差异不仅在于x,而且还具有任何值。
整齐的削减
有限域和简单多项式的概念似乎牵强,并且对研究数字的特性毫无用处。 但是它们看起来像飓风模拟器-本身就是一个宇宙,给出了在大世界中发生的现象的想法。
Shusterman说:“在整数和多项式之间有一个古老的类比,它使您可以将与整数有关的可能非常复杂的问题转换为与多项式有关的任务,这些任务也可能很复杂,但可能更容易解决,” Shusterman说。
1940年,当
安德烈·韦尔(Andre Weil)开发了将小数系统的算术转换为整数的精确方法时,有限域就广为人知。 韦尔(Weil)通过这种联系获得了惊人的结果。 他
证明了数学上最重要的问题-黎曼假设-对于在有限域上具有一组曲线的情况(此问题被称为黎曼几何假设的名字)。 该证明以及一组其他的
Weyl假设使有限域成为数学发现的丰富领域。
韦尔(Weil)的主要思想是,在有限域中,可以使用几何技术找到有关数字问题的答案。 “这是有限域的特征。 舒斯特曼说:“您要解决的许多任务可以从几何上重新表述。”
要了解几何在这种环境中的外观,请将每个多项式想象为空间中的一个点。 多项式的系数用作确定其位置的坐标。 返回到我们的1、2和3的最终字段,多项式2x + 3位于二维空间的点(2,3)。
但是,即使在最简单的有限空间中,也存在无限数量的多项式。 可以通过增加最大指数或表达程度的指数来创建更复杂的多项式。 在我们的情况下,多项式x 2-3x-1将由三维空间中的一个点表示。 多项式3x
7 + 2x
6 + 2x 5-2x 4-3x
3 + x 2-2x + 3将由八维空间中的点表示。
在新工作中,此几何空间表示给定有限域的给定度数的所有多项式。 问题变成了:有没有办法隔离所有表示简单多项式的点?
Savin和Shusterman的策略是将空间分为两部分。 在一个部分中,将存在与具有偶数个因子的多项式相对应的所有点。 另一方面,所有点都对应于具有奇数个因子的多项式。
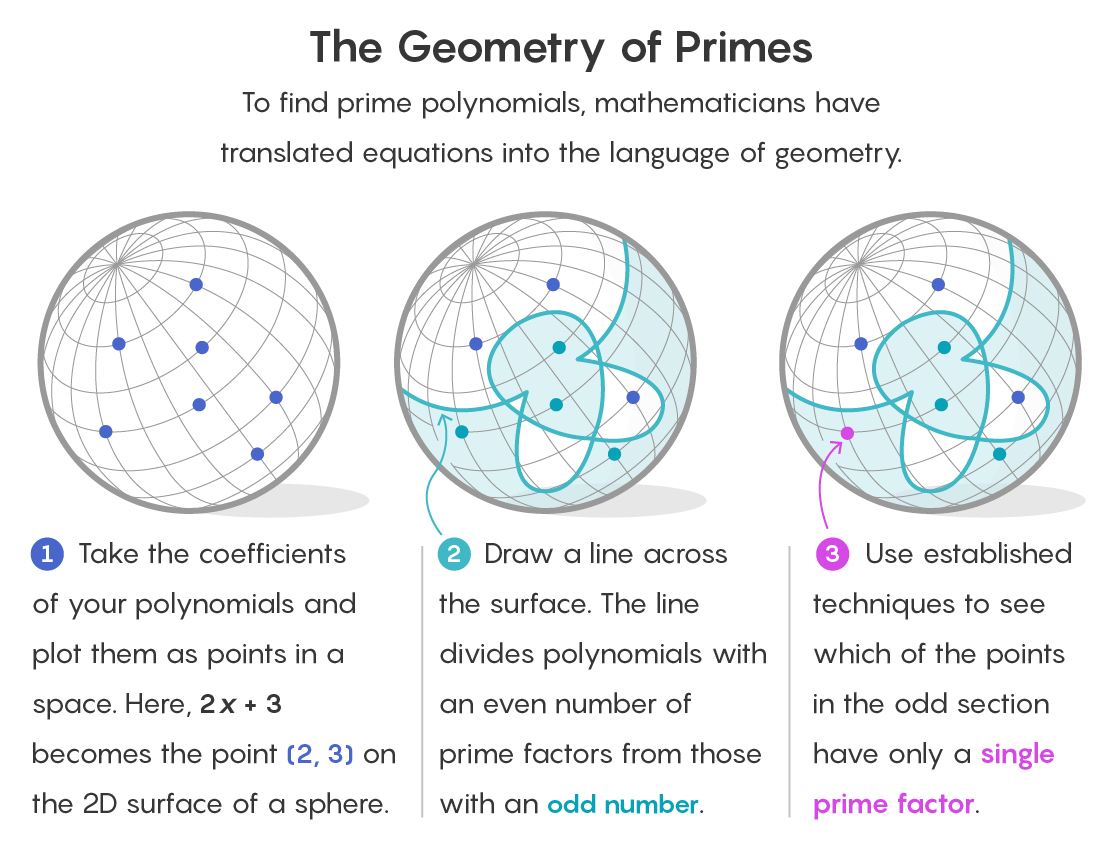
这已经简化了任务。 有限域的简单孪生多项式的假设仅适用于具有一个因子的多项式(就像素数有一个因子一样,它本身就是)。 并且由于数字1是奇数,因此可以立即丢弃包含偶数个因子的多项式的部分空间。
诀窍是使用除法。 对于二维物体(例如球体的表面),它被一维曲线切成两半-就像赤道切开地球的表面一样。 尺寸较大的对象始终可以用尺寸小于1的对象切割。
但是这些尺寸较小,划分多项式空间的形式根本不像赤道那么优雅。 它们是根据称为
Mobius函数的数学公式绘制的。 在输入处,它采用多项式;在输出处,如果多项式具有偶数个质数,则给出1 .;如果其具有奇数,则给出-1;如果因式分解,则给出0(因为16可以分解为2× 2×2×2)。
Mobius函数绘制的曲线像疯狂一样弯曲和扭曲,在许多地方与它们自己相交。 这些被称为奇点的位置特别难以分析(它们对应于可以分解为几个相同质数的多项式)。
Savin和Shusterman的根本创新在于,他们找到了将较少测量值的回路切成较短段的确切方法。 这些部分比整个循环更容易学习。
Savin和Shusterman编写了包含奇数个素数的多项式目录(这是最困难的)后,面临着确定哪些简单和哪些是双胞胎的任务。 为此,他们应用了数学家用来研究普通数中素数的几种公式。
Savin和Shusterman用他们的技术证明了某些有限域中关于简单多项式的两个重要观点。
首先,有限域中的孪生素数的假设是正确的:存在成对的孪生多项式对,它们的对数之间存在任意给定值。
其次,更重要的是,这项工作提供了在一定顺序的多项式中可以找到的简单双多项式数量的准确计数。 这类似于知道在数字线上足够长的时间间隔内有多少个双素数-这只是数学家的梦想。
特拉维夫大学的齐夫·鲁德尼克(Ziv Rudnik)说:“这是第一份定量比较类推整数的著作,这是一个非常出色的结果。” “到目前为止,没有发生这样的事情。”
Savin和Schusterman的证明表明,在安德烈·威尔(Andre Weil)证明有限域曲线的黎曼假说近80年后,数学家仍然顽固地朝这个方向发展。 现在,处理孪生素数假设的数学家将转向Savin和Shusterman的著作,也许它将为他们提供深刻的启发。