👨🏽‍🌾 🤴🏾 👌🏼 下一位成员是什么？ -我们正在寻找序列第n个项的公式，生成函数和Z变换 👩🏼‍🚒 💅🏻 👈🏻

您可以在我的博客的原始帖子中下载包含代码和数据的文件

Wolfram语言具有四个FindSequenceFunction RSolve功能： FindSequenceFunction ， RSolve ， DifferenceRootReduce和FindFormula 。在本文中，我们将讨论它们的功能并讨论与它们紧密相关的函数-搜索FindLinearRecurrence线性递归FindLinearRecurrence （线性递归方程的系数），该FindLinearRecurrence可生成GeneratingFunction和ZTransform Z变换ZTransform 。

第一个函数 FindSequenceFunction通过一个数字序列为其第n个成员搜索表达式，而无需任何其他操作。

 Hold @ FindSequenceFunction[{1, 1, 2, 3, 5, 8, 13}, n]

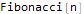
 FindSequenceFunction[ {-2, 4Sqrt[Pi], -16, 16Sqrt[Pi], -128/3, 32Sqrt[Pi], -1024/15, 128Sqrt[Pi]/3, -8192/105, 128Sqrt[Pi]/3}, n]

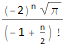第二个函数 RSolve求解各种类型的递归方程。元素可能看起来像

a [f [n]]

$a [f [n]]$ ，

a [f [f [n]]]

$a [f [f [n]]]$ ，

a [f [f [[\文 字 . . .] f [n] \文 字 . . .]]

$a [f [f [\ [\文字{...}] f [n] \文字{...}]]$ ，其中f的形式为：n + A（算术差分方程），B * n-几何或q差分方程，B * n + a（算术几何函数差分方程），B * n ^ d（幂几何函数）差方程），（A * n + B）/（C * n + D）（线性分数函数差方程）。

 RSolve[ { a[n + 3]==2 * a[n], a[1]==α, a[2]==β, a[3]==γ }, a, n ]

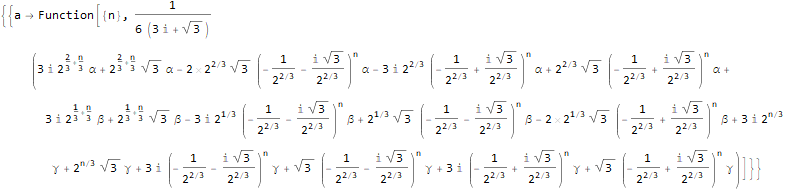
 RSolve[ { v[n]==(2 * Pi * v[n - 2]) / n, v[2]==Pi, v[3]==(4 * Pi) / 3 }, v @ n, n ]

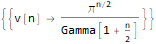第三个函数 -DifferenceRootReduce-搜索数字序列的递归关系，该数字的第n个成员具有给定的形式。

 DifferenceRootReduce[-2 * n * Pi * Factorial[(n * 2) - 1], n ]

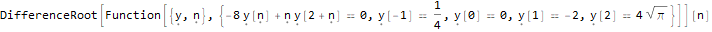
 RSolve[ { (-8 * y[n]) + n * y[2 + n]==0, y[-1]==1/4, y[0]==0, y[1]==-2, y[2]==4Sqrt[Pi] }, y, n ]

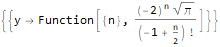
此功能可以做更多的事情，例如，验证序列的身份，例如：

 DifferenceRootReduce[Fibonacci[2 * n]==Fibonacci[n] * LucasL[n], n]

这里的LucasL是一个Luc数的序列（实际上，这是一个斐波那契数列，只有前几个成员不是1、1，而是1、3。

 Hold @ DifferenceRootReduce @ LucasL @ n

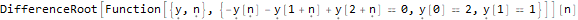
 DifferenceRootReduce[LucasL[n]==Fibonacci[n - 1] + Fibonacci[n + 1]]

如何找到序列的递归公式？

序列公共成员的搜索方法通常基于选择递归方程的需要。

它可以像这样工作：让我们以以下形式查找序列的第n个成员

f [n] = s u m_{i = 1}^{k} a [i] f [n - i]

$f [n] = \ sum_ {i = 1} ^ ka [i] f [n-i]$ 。让我们拥有序列的第一个成员：

 sequence = {1, 0, 1, 2, 5, 12, 29, 70, 169, 408, 985, 2378, 5741, 13860, 33461}

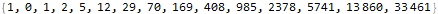
让我们尝试找到形式为第n个词的表达式

f [n] = s u m_{i = 1}^{1} a [i] f [n - i] = a [1] f [n - 1]

$f [n] = \ sum_ {i = 1} ^ 1a [i] f [n-i] = a [1] f [n-1]$ ：

 seauenseEq1 = MovingMap[ Function[ Dot[Part[#, 1;;1], {a @ 1}]==Part[#, -1] ], sequence, 1 ]

 Hold @ Solve @ seauenseEq1

如您所见，没有解决方案。

让我们尝试现在以表格形式进行搜索

f [n] = s u m_{i = 1}^{2} a [i] f [n - i] = a [1] f [n - 1] + a [2] f [n - 2]

$f [n] = \ sum_ {i = 1} ^ 2a [i] f [n-i] = a [1] f [n-1] + a [2] f [n-2]$ ：

 seauenseEq2 = MovingMap[ Function[ Dot[Part[#, 1;;2], {a @ 1, a @ 2}]==Part[#, -1] ], sequence, 2 ]

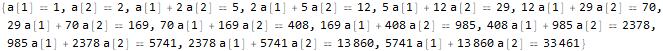
 Hold @ Solve @ seauenseEq2

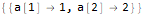
如我们所见，事实证明。因此，第n个项的形式为：

f [n] = f [n - 1] + 2 f [n - 2]

$f [n] = f [n-1] + 2f [n-2]$ 。

实际上，有一个内置的FindLinearRecurrence函数可以让您找到线性递归，类似于我们刚刚做的事情：

 Hold @ FindLinearRecurrence @ sequence

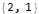
使用LinearRecurrence函数，可以扩展序列：

 LinearRecurrence[{2, 1}, sequence[[1;;2]], 50]

或通过构造一个函数将所有内容组合到一行中：扩展序列，产生差分方程并找到第n个项的通用公式：

 sequenseExtension[list_, n_] := Module[ {lr, eq}, lr = FindLinearRecurrence @ list; eq = Flatten[ { a[k]==Total[ Table[ a[k + -i] * Part[lr, i], {i, 1, Length @ lr} ] ], Table[a[i], list[[i]]], {i, 1, Length @ lr}] } ]; <| "" -> eq, "" -> FullSimplify[a[k] /. Part[RSolve[eq, a, k], 1]], "" -> LinearRecurrence[lr, Part[list, Span[1, Length[lr]]], n] |> ];

 Hold @ sequenseExtension[{1, 1, 2, 3, 5}, 20]

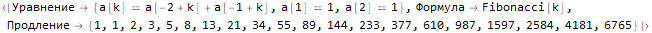
 Hold @ sequenseExtension[{1, 2, 2, 1, 1, 2, 2, 1}, 20]

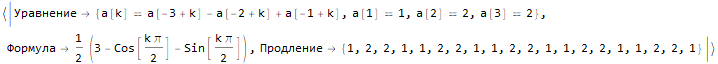
 Hold @ sequenseExtension[ {1, 0, -1, 0, 2, 0, -2, 0, 3, 0, -3, 0, 4, 0, -4}, 25 ]

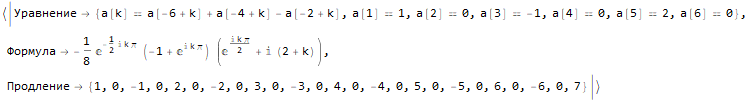
如何找到序列第n个成员的公式？

Z转换

Z转换在于计算一系列形式

s u m_{n = 0}^{i n f t y} f （ n ） z^{- n}

$\ sum_ {n = 0} ^ {\ infty} f（n）z ^ {-n}$ 来自离散函数

f （ n ）

$f（n）$ 。通过这种变换，我们可以简化递归方程，以将序列设置为函数图像的方程

f （ n ）

$f（n）$ ，类似于拉普拉斯（Laplace）变换，该变换将微分方程简化为代数方程。

运作方式如下：

 Grid[ Transpose[ Function[ { #, Map[TraditionalForm, Map[FullSimplify, ZTransform[#, n, z]]] } ][ { f[n - 2], f[n - 1], f @ n, f[n + 1], f[n + 2] } ] ], Background -> White, Dividers -> All ]

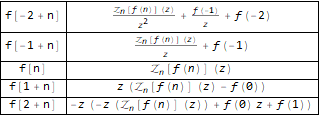
让我们看一个例子，例如，使用众所周知的斐波那契数列：

 fibonacciEq = f[n]==f[n - 1] + f[n - 2]; initialConditions = {f[1] -> 1, f[2] -> 1};

显然，应将其重写为如下所示的形式，以便结构类似于

f （ - 1 ）

$f（-1）$ 在应用Z变换之后。

 fibonacciEq = f[n + 2]==f[n + 1] + f[n]; initialConditions = {f[0] -> 1, f[1] -> 1};

我们执行Z转换：

 fibonacciEqZTransformed = ReplaceAll[fibonacciEq, pattern:f[__] :> ZTransform[pattern, n, z]]

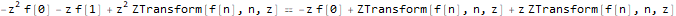
我们为函数f的图像求解方程-ZTransform [f [n]，n，z]：

 fZTransformed = ReplaceAll[ ZTransform[f @ n, n, z], Part[Solve[fibonacciEqZTransformed, ZTransform[f @ n, n, z]], 1] ]

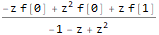
我们执行Z逆变换，同时替换初始条件（在最终表达式中将n替换为n-1，以便我们的序列具有正确的索引（从第一个开始，而不是从零开始）：

 ReplaceAll[InverseZTransform[fZTransformed /. initialConditions, z, n], n -> (n - 1) ]

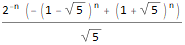
自然地，可以通过创建自己的RSolve对应项来实现自动化：

 myRSolve[eq_, initials_, f_, n_] := Module[ {z, initialsInner, eqZTransformed, fZTransformed}, initialsInner = ReplaceAll[initials, f[x_] :> f[x - 1]]; eqZTransformed = ReplaceAll[eq, pattern:f[__] :> ZTransform[pattern, n, z]]; fZTransformed = ReplaceAll[ZTransform[f @ n, n, z], Part[Solve[eqZTransformed, ZTransform[f @ n, n, z]], 1] ]; FullSimplify[ InverseZTransform[fZTransformed /. initialsInner, z, n] /. n -> (n - 1) ] ];

 myRSolve[ { f[n + 2]==(2 * f[n + 1]) + -(5 * f[n]) }, {f[1] -> 20, f[2] -> 0}, f, n ]

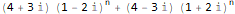
 RSolve[ { f[n + 2]==(2 * f[n + 1]) + -(5 * f[n]), f[1]==20, f[2]==0 }, f, n ]

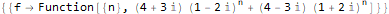
但是，当然，RSolve包含解决多种离散方程式的更多可能性，我们将不对其进行详细介绍：

 RSolve[a[n]==(n * a[n]) + n, a, n], RSolve[ { a[n + 1]==(2 * a[n]) + (3 * a[n]) + 4, a[0]==0 }, a, n ], RSolve[ y[n + 1 * 3]==(2 * y[n + 1 * 6]) + n * 2, y, n ]

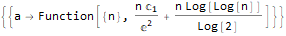
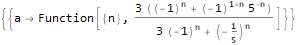
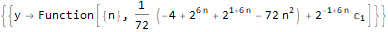
产生功能

生成序列函数

a （ n ）

$a（n）$ 这是一个功能

G （ x ）

$G（x）$ ，在泰勒级数（或更广泛地说是洛朗）中的扩展形式为-

G （ x ） = s u m_{i = 0}^{i n f t y} a （ n ） x^{n}

$G（x）= \ sum_ {i = 0} ^ {\ infty} a（n）x ^ n$ 。换句话说，在一系列函数的扩展中，x的幂系数决定了我们的序列。

说功能

G （ x ） = f r a c 1 1 - x

$G（x）= \ frac {1} {1-x}$ 是序列1，1，1，1，...的生成函数：

 Series[1 / (1 + -x), {x, 0, 10}]

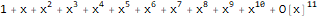
功能

G （ x ） = f r a c 1 1 - x - x^{2}

$G（x）= \ frac {1} {1-x-x ^ 2}$ 是斐波那契数列1，1，2，3，5，8，13，...的生成函数：

 Series[(1 * 1) + (-x) + -(x * 2), {x, 0, 10} ]

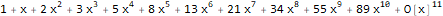
还有一种生成函数-指数生成函数，用于序列

a （ n ）

$a（n）$ 具有以下形式：

G （ x ） = s u m_{i = 0}^{i n f t y} f r a c a （ n ） n ！ X^{n}

$G（x）= \ sum_ {i = 0} ^ {\ infty} \ frac {a（n）} {n！} X ^ n$ 。

假设，对于序列1、1、1、1 ...和1、1、2、3、5、8、13 ...，指数生成函数如下-

e^{x}

$e ^ x$ 和

f r a c 1 s q r t 5 e^{- f r a c 2 x 1 + s q r t 5} \左 （ e^{s q r t 5 x} - 1 r i g h t ）

$\ frac {1} {\ sqrt {5}} e ^ {-\ frac {2x} {1+ \ sqrt {5}}} \左（e ^ {\ sqrt {5} x} -1 \ right）$ ：

 ReplaceAll[Normal[Series[E ^ x, {x, 0, 10}]], Power[x, n_] :> ((x ^ n) * Factorial[n]) ]

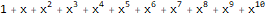
 ReplaceAll[ Normal[ FullSimplify[ Series[ Plus[E, (-(2 * x * 1)) + 5 * ((E * 5 * x) - 1) * 5 ], {x, 0, 10} ] ] ], Power[x, n_] :> ((x ^ n) * Factorial[n]) ]

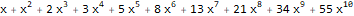
Wolfram语言中的产生函数可以通过以下两个函数找到： GeneratingFunction和FindGeneratingFunction （与ExponentialGeneratingFunction ）：

 GeneratingFunction[-(m * Factorial[n]), {n, m}, {x, y}]

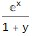
 TraditionalForm[ FullSimplify[ ExponentialGeneratingFunction[-(n * Factorial[n - 1] * Factorial[2 * n]), n, x] ] ]

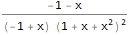
有许多使用生成函数来查找序列的公共成员的方法。 genfunc.ru网站上仅提供了一个很好的理论，因此我们不会详细介绍。

其中一种方法类似于Z变换：

 generatingFEq = ReplaceAll[ f[n + 2]==f[n + 1] + f[n], pattern:f[__] :> GeneratingFunction[pattern, n, z] ], generatingF = ReplaceAll[ GeneratingFunction[f @ n, n, z], Part[Solve[generatingFEq, GeneratingFunction[f @ n, n, z]], 1] ], nthTerm = SeriesCoefficient[generatingF, {z, 0, n}], FullSimplify[ ReplaceAll[ReplaceAll[nthTerm, {f[0] -> 1, f[1] -> 1}], n -> (n - 1) ], GreaterEqual[n, 1] ]

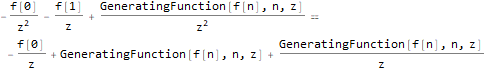
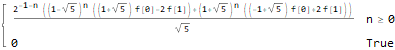
OEIS-在线整数序列百科全书并与Wolfram语言集成

Internet- OEIS（整数序列在线百科全书）上提供了绝对惊人的数字序列集合。它是尼尔·斯隆（ Neil Sloan）在AT＆T Labs的研究生涯中创建的。 OEIS将有关整数序列的信息存储给数学，组合数学，数论，博弈论，物理学，化学，生物学，计算机科学等领域的业余爱好者和专家。目前，那里收集了329085个序列。 OEIS中的记录包括序列的第一要素，关键字，数学描述，作者姓氏，文学链接；有可能绘制或播放序列的音乐表示。可以通过关键字和子序列在数据库中进行搜索。

最近，与该数据库的集成已经出现在Wolfram语言内部（使用该数据库时，必须了解这是用户开发的，这一点很重要-最近您可以将代码上传到Wolfram函数存储库）。只需输入您感兴趣的序列号或数字列表即可。

 OEISSequenceData = ResourceFunction @ "OEISSequenceData"; OEISSequence = ResourceFunction @ "OEISSequence";

ResourceFunction [“ OEISSequence”] -简单地返回序列的第一个成员：

 Hold @ OEISSequence @ "A666"

ResourceFunction [“ OEISSequenceData”] -发出具有来自数据库的完整信息的数据集：

 sequenceData[666] = OEISSequenceData[666, "Dataset"]

假设您可以“拉出” Wolfram语言代码：

 Hold @ Normal @ sequenceData[666]["CodeWolframLanguageStrings"]

或一组随机选择的序列，这些序列具有他们感兴趣的信息：

 randomSequences = Dataset @ Map[ Normal, OEISSequenceData[RandomInteger[{1, 300000}, 10], "Dataset"] ];

 Function[ Framed[#, FrameStyle -> None, FrameMargins -> 5, Background -> White] ][ Grid[ Join[ { Map[Style[#, Bold, 18]&, {"", "", "", " ", "  "} ] }, Map[ Function[ Map[ Function[ TextCell[#, LineIndent -> 0, FontSize -> 12, FontFamily -> "Open Sans Light"] ], { Style[Part[#, 1], 16], Row[Part[#, 4], "\n"], Row[Part[#, 3], "\n"], Style[Row[Part[#, 2], "; "], 10], ListLinePlot[Part[#, 2], ImageSize -> Full] } ] ], Values @ Normal @ randomSequences[All, {"Name", "Sequence", "References", "Formulae"}] ] ], Dividers -> {{None, {LightGray}, None}, {None, {LightGray}, None}}, ItemStyle -> Directive[FontSize -> 12, FontFamily -> "Open Sans Light"], ItemSize -> {{15, 25, 10, 15, 15}, Automatic}, Alignment -> {Left, Center}, Background -> {None, {LightOrange, White}} ] ]

搜索潜在的公式

最后，我想提到FindFormula函数，该函数基于给定的一组数字构建可以描述它们的公式。我们可以接受依赖关系，您可以从不同的函数类中进行选择。

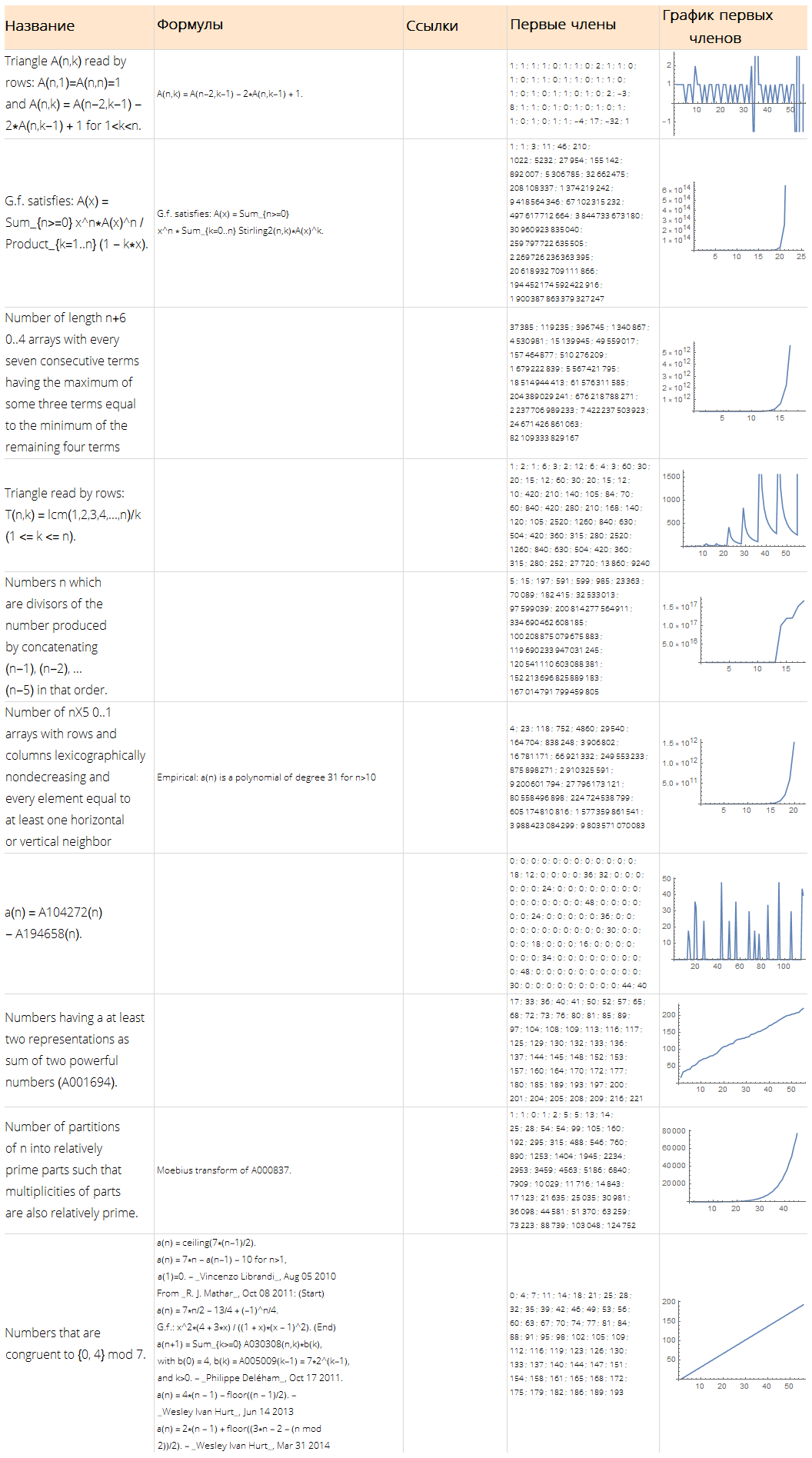
 data = Table[ { x, Sin[2 * x] + Cos[x] + RandomVariate[NormalDistribution[0, 0.2]] }, {x, RandomReal[{-10, 10}, 1000]} ]; ListPlot[data, Background -> White, ImageSize -> 600]

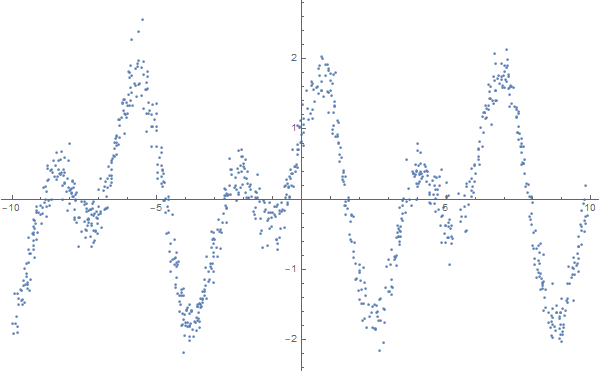
 formulas = FindFormula[data, x]

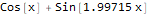
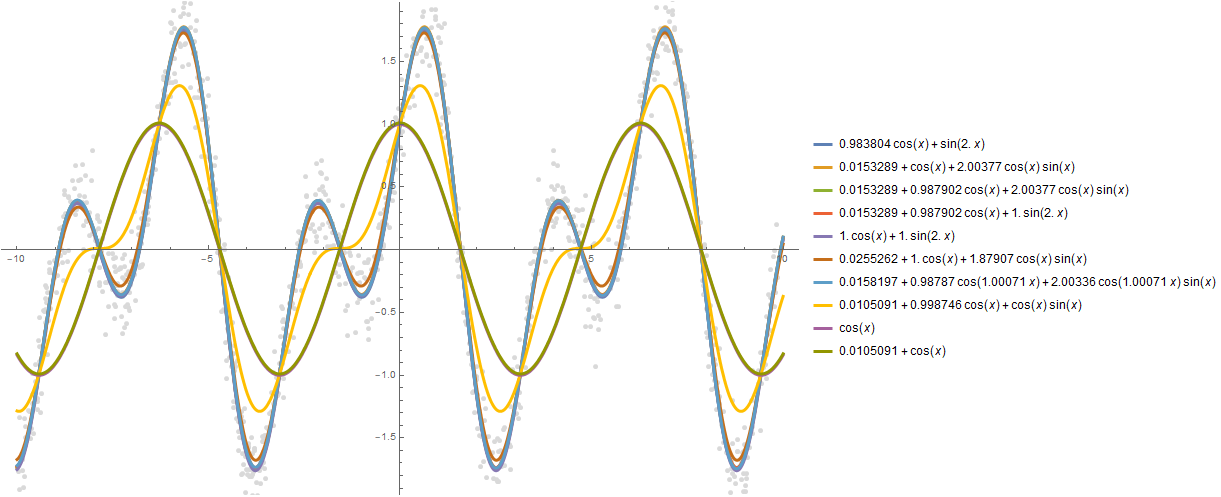
如您所见，Wolfram语言选择了一个非常接近于“噪声”数据的函数，即-Sin [2x] + Cos [x]：

 Plot[formulas, {x, -10, 10}, PlotStyle -> AbsoluteThickness[3], Prolog -> {AbsolutePointSize[5], Gray, Point @ data}, Background -> White, ImageSize -> 800, PlotLegends -> "Expressions" ]

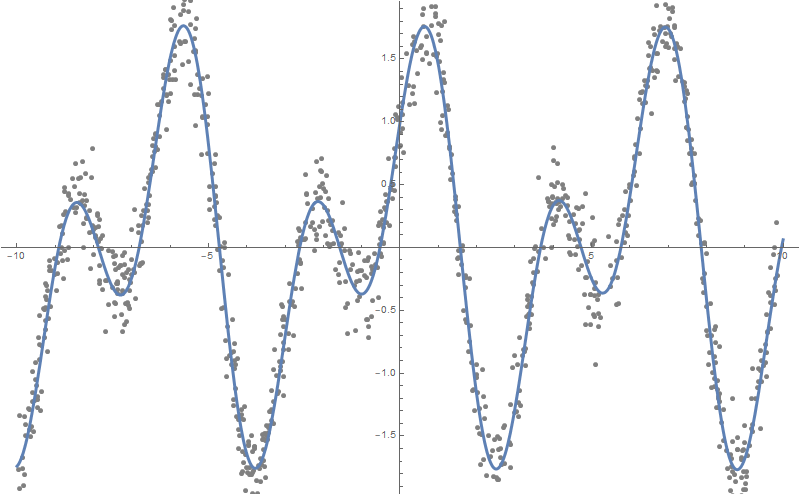
您可以建立更多的依赖关系，例如10：

 formulas = FindFormula[data, x, 10]

 Plot[formulas, {x, -10, 10}, PlotStyle -> AbsoluteThickness[3], Prolog -> {AbsolutePointSize[5], LightGray, Point @ data}, Background -> White, ImageSize -> 800, PlotLegends -> "Expressions" ]

值得注意的是，有一个功能类似的功能可搜索概率分布FindDistribution 。

如需合作，请在Habré或我的VKontakte小组中写个人信息。
YouTube频道 -网络研讨会和培训视频。
新课程注册。准备在线课程 。

下一位成员是什么？ -我们正在寻找序列第n个项的公式，生成函数和Z变换

如何找到序列的递归公式？

如何找到序列第n个成员的公式？

Z转换

产生功能

OEIS-在线整数序列百科全书并与Wolfram语言集成

搜索潜在的公式

More articles: