DMK出版社出版了《奥林匹克编程》一书,副标题为“研究和改进比赛中的算法”。 对于那些有兴趣,准备和准备参加或者只是计划未来的人们来说,这已经成为一种新鲜空气,参加诸如各种体育节目活动之类的智力活动。 在俄罗斯,他们并不熟悉。
在莫斯科物理技术学院及其领导Alexei Maleev,Mail.Ru集团以及莫斯科工场ICPC项目的支持下,出版了俄文版的“竞争性编程指南”(施普林格国际出版公司)。

“奥林匹克编程每年都在学生中越来越流行。 这方面的一个很好的例子是,在2019年,我们莫斯科工场ICPC,我们将在11月在世界各地举行第十次世界杯训练营筹备工作,他们已经在新加坡,欧洲和南美以及俄罗斯-从符拉迪沃斯托克(Vladivostok)到莫斯科。 10月初,莫斯科编程竞赛在莫斯科举行,有2284人参加了莫斯科大学18个场馆的比赛,这是在Rosmolodezh的支持下举办的竞赛规模的绝对记录。
我们对他们的生动兴趣感到非常高兴,并准备以各种方式支持它-例如,对于莫斯科大学的学生,我们将在最好的培训师的陪同下为ICPC进行免费培训。 当然,对于参与者来说,巩固材料,分解任务并增强他们的知识总是有用的。 因此,我很高兴看到您的书出现了,我对此表示祝贺。 我们希望,在2020年6月在莫斯科举行的ICPC决赛中,已经有那些读过它的人成为第二届增补版的英雄。”
阿列克谢·马列夫(Alexey Maleev),莫斯科ICPC 2020世界杯决赛决赛的负责人,莫斯科物理技术学院副院长,莫斯科研讨会ICPC项目的创始人。
“竞争性编程指南”已从英语翻译成俄语。 除英语和俄语外,还发行了韩文出版物。
该书的作者是来自赫尔辛基阿尔托大学(芬兰)[3]的教师和研究员Antti Laaxsonen,他在编程和算法教学方面拥有丰富的经验,并且是国际编程比赛中芬兰团队的教练。 他在Codeforces门户网站上的昵称为“ pllk” [4],具有很高的评分2347和“国际大师”地位。 2008年,他A. Laaxsonen成为他所在国家的信息学奥林匹克组织者之一。 2016年-波罗的海奥林匹克信息学科学主管。
本书的目标读者都对奥林匹克编程感兴趣,并且/或者正在从事奥林匹克编程领域的工作。 但是,为了完全吸收材料,需要具备编程基础知识,而作者并不需要读者体验设计算法和参加奥林匹克运动会的经历。 所有这些使我们能够向众多感兴趣的读者推荐这项工作。 对于初学者来说,它将成为现代奥林匹克编程的入门,经验丰富的专家将帮助系统化知识,并将成为他们的参考工具。
书中材料的提交是从简单到复杂的。 首先,他熟悉了本书的目的和目标,奥林匹克编程,任务CSES [5]的收集以及其他有关奥林匹克编程的书籍。
在获得必要的理论基础之后,读者将准备继续练习。 编程技术是下一个主题。 在其中,作者包括了C ++语言(C11标准)的基础知识,该语言实现了本书中的所有示例。 递归算法和按位运算的分析。
在本书的各章中,读者将能够找到有关大多数“标准”主题的信息以及为奥林匹克竞赛参与者提供的算法实现示例:数据结构,动态编程,图形算法和树算法,范围查询以及使用字符串。
另外,我想强调本书的许多章节。 例如,“算法的选定设计问题”一章。 它包括可并行查看排放,折旧分析和查找最小值的算法。 为读者提供了查找汉明距离的算法,图形中可达到性问题的解决方案,两指针方法,三元搜索,总和的最小化以及“奥林匹克”及其教练员的其他有趣主题。
作为示例,我将在“设计算法的选定问题”一章中给出任务示例。
让我们考虑具有并行查看位的算法,其中按位运算用于有效的数据处理。 在典型情况下,我们可以使用按位运算来替换for循环,从而大大减少了算法的运行时间。
并行浏览算法
并行查看数字的算法基于以下事实:可以使用按位运算并行操作数字的各个数字。 因此,一种设计算法的方法是以一种可以使用按位运算有效地实现它们的方式来展示算法的步骤。
汉明距离汉明距离
相同长度的线a和b之间的汉明(a,b)是这些线不同的位置数。 例如:
汉明(01101,11001)= 2。
考虑以下任务:给定n个长度为k的位串,计算两个串之间的最小汉明距离。 例如,对于第[00111,01101,11110]行,答案为2,因为
- 汉明(00111,01101)= 2;
- 汉明(00111,11110)= 3;
- 汉明(01101,11110)= 3。
可以通过计算每两行之间的汉明距离来“正面解决”该问题。 这种算法的时间复杂度为(n
k)。 要计算线a和b之间的距离,请使用以下函数:
int hamming(string a, string b) { int d = 0 for (int i = 0; i < k; i++) { if (a[i] != b[i]) d++; } return d; }
但是由于字符串由位组成,因此可以通过将字符串存储为整数并使用按位运算来计算它们之间的距离来优化解决方案。 特别是,如果k≤32,则可以将字符串存储为int类型的值,并使用以下函数计算距离:
int hamming(int a, int b) { return __builtin_popcount(a^b); }
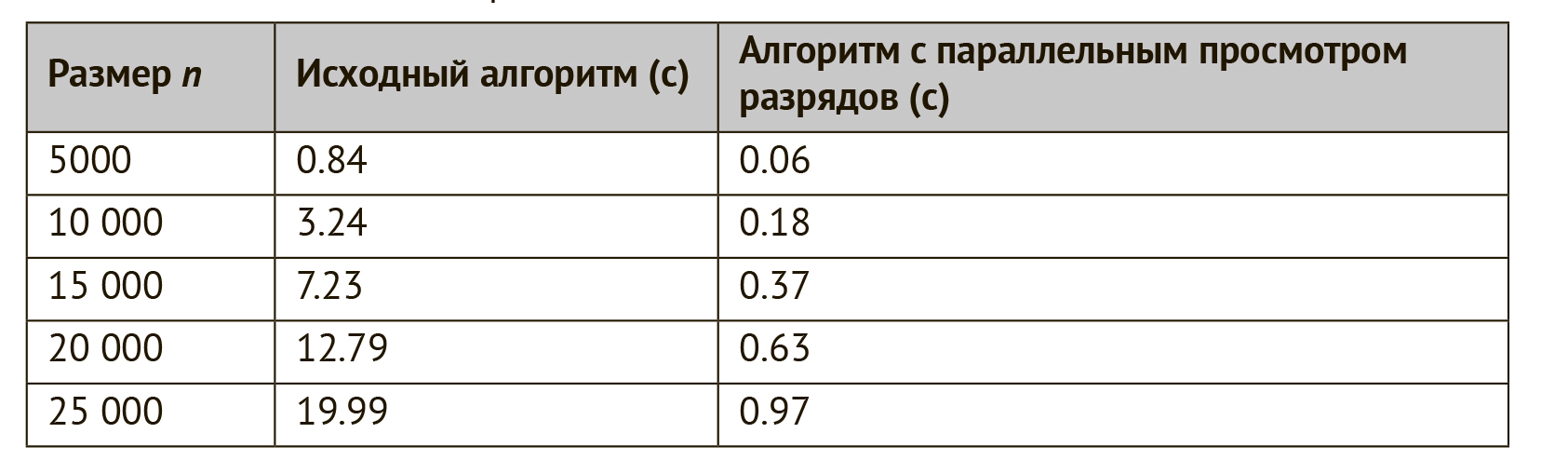
在这里,异或运算会建立一条直线,其中单位位于a和b不同的位置。 然后,通过__builtin_popcount函数计算单位位数。 该表显示了在现代计算机上,将原始算法与该算法与位的并行视图进行比较的结果。 并行查看位的算法实际上要快20倍左右。
表:计算长度为k = 30的n个位串的最小汉明距离的算法的运行时间
值得一提的是“数学”和“几何”两章。 正如读者已经猜到的那样,他们致力于通过C ++编程语言和适当算法的构建来解决数学和几何问题。 在“数学”一章中,我们在等待五个大主题:“数论”,“组合论”,“矩阵”,“概率”和“博弈论”。 并且在“几何”中:“几何中的技术手段”,“基于扫描线的算法”。 因此,用于解决数学和几何问题的算法构造的复杂表述使这本书成为“奥林匹克竞赛”的“发现”,因为在有关该主题的书籍短缺的背景下,这是很少的。
笔者决定将许多问题放在“其他主题”一章中。 他们的发展“有时可以帮助解决最困难的奥林匹克运动问题”。 这些是“算法中的平方根”,“以及关于分段树的再次”,“ Duchi”,“动态编程的优化”和“其他”。 根据附加说明的名称,它们需要分段树和不同事物上的副标题。
至于分段树,读者将熟悉延迟传播,动态树,顶点处的数据结构,二维树。 在“其他”中,他正在等待:中间的一个会议(将搜索空间分成大致相等的两个部分,在每个部分中进行搜索,然后组合结果),计数集,并行二进制搜索,动态连接。
完成有关数学和广泛书目的书参考信息(32个来源)。
因此,Antti Laaxsonen撰写的“奥林匹克编程”一书是体育编程领域的精彩介绍。 同时,还有很棒的参考指南。 这本书适合初学者“ olympiadnikov”,将有助于组织经验丰富的知识。 这对教练很有用。
再次,我们注意到书中的所有示例都是用C ++编程语言实现的。 奥运会对他的需求最大。 但是有人可能会发现这是本书的缺点,因为其他语言很流行-Python,Java。 那些喜欢这些编程语言的人可以用自己喜欢的语言解决一本书中提出的问题。 这将是一个很好的锻炼。 最终,正是在寻找最佳解决方案的过程中,奥运会任务才得以完成。
本文的作者:Igor Shtompel,
《系统管理员》杂志
“职业\教育”部分的作者和演示者