两项具有纪念意义的著作说服了许多数学家放弃了等号。 他们的目标是借助弱关系（“对等”）重建学科的基础。 而且这个过程并不总是能顺利进行。
等号是数学的基石。 他似乎发表了一个基本而一致的声明：这两个实体完全相同。
但是，关于数学的初始误差，以等号表示的数学家圈子正在扩大。 他们认为这是一种外部现象，掩盖了数量之间关系的重要复杂性-这种复杂性可以解决许多问题。 他们想使用宽松的对等语言来改革数学。
杜克大学的
乔纳森·坎贝尔说：“我们产生了平等的思想。” “应该在它的位置上具有等效性。”
这个社区中最杰出的人物是
雅各布·卢里 （
Jacob Lurie） 。 今年7月，现年41岁的
卢里（Lurie）辞去了哈佛大学的全职工作，在普林斯顿高等研究院担任教职，一些世界上最杰出的数学家在那里工作。
像卢瑞这样规模的想法几乎在任何领域都找不到。 在跨越数千页的书中，他充斥着技术细节，他创造了一种与通常理解数学最基本概念的方式不同的方式，超越了等号。 哈佛大学数学家兼研究生院院长
迈克尔·霍普金斯说：“我认为这似乎是对数学的正确思考方式。”
他于2009年出版了他的第一本书《
高等理论》 。这本944页的书以“无穷大类”的新语言解释了公认的数学领域。 在随后的几年中，卢瑞（Lurie）的思想渗透到了广泛的数学学科中。 许多数学家认为它们对于该领域的未来必不可少。 西北大学的
约翰·弗朗西斯 （
John Francis）说：“在研究了无穷大的类别之后，没有人会是一样的。”
雅各布·卢里但是，无穷大类别的传播揭示了一个受人尊敬的数学领域所经历的所有问题，试图吸收新的大胆观点，尤其是挑战其最重要概念的观点。 爱丁堡大学的
克拉克·巴威克 （
Clark Barwick）说：“数学界有一定程度的保守主义。” “我不认为任何一组数学家都会在没有令人信服的理由的情况下迅速接受任何工具。”
尽管许多数学家已经接受了无穷大的范畴，但很少有人读过Lurie的冗长而极其抽象的全部文章。 结果，根据他的思想所做的部分工作变得不像数学所接受的那样严格。
康奈尔大学的数学家
Inna Zakharevich说：“我听到人们说：'Lurie在某处有它。' -我说：“真的吗？ 您指的是8,000页文字。 这不是参考，而是对权威的呼吁。”
数学家仍在努力实现卢里（Lurie）思想的广度和表达思想的独特方式。 他们提取了他介绍无穷大类别的本质，并将其呈现在新包装中，以便更多的数学家可以使用它。 从某种意义上说，他们进行了必要的领导，必须跟随任何革命，将革命文本转化为日常的法律法规。 因此，他们创造了数学家的未来，而不是基于平等，而是基于平等。
无尽等效塔
数学平等似乎是所有观点中争议最小的。 两珠加一珠等于三珠。 还有什么要谈的？ 但是，最简单的想法可能最具欺骗性。
自19世纪末以来，数学的基础就建立在称为集合的对象集合上。 集合论为这些集合的创建和处理设定了规则或公理。 例如，这些公理之一声称可以将一个元素的集合添加到两个元素的集合中，并获得三个元素的新集合：2 +1 = 3。
证明两个量相等的正式方法是将对配对。 将等号右边的一个小珠与左边的一个小珠配对。 在所有比较之后，将不再有多余的珠子。
集合论认识到，两个由三个对象组成的集合可以彼此精确匹配，但并不意味着进行这种比较的所有可能方式。 右边的第一个珠子可以以左边第一个珠子的形式拾取一对，或者将右边的第一个珠子与左边的第二个珠子匹配，依此类推（可以有六个这样的对）。 说2加1等于3，并以此结束，则意味着不要看到所有等同于它们的可能方法。 坎贝尔说：“问题是配对的方式很多。” “当我们说平等时，我们就会忘记他们。”
这就是等效性发挥作用的地方。 如果平等是明确的关系-两件事是平等的或不平等的-平等可以是不同的。
当您将一个集合中的每个元素与另一个集合中的每个元素精确匹配时，您将获得很强的对等性。 但是，例如，在诸如
同调的数学领域中，如果可以通过拉伸或压缩将一种形式转换为另一种形式而不破坏其形式，则两种形式（或几何图形）是等效的。
从同构理论的角度来看，平盘和空间中的点是等效的-可以将磁盘压缩到一个点。 但是，您无法将磁盘上的点与点上的点进行匹配。 的确，点的盘数是无限的，而点仅是一个点。
自20世纪中叶以来，数学家一直在尝试开发一种替代集合理论的方法，在该理论中，数学在等价性方面会更容易处理。 1945年，数学家
Samuel Eileberg和
Saunders MacLane引入了一个具有内在等效性的新基本对象。 他们称其为类别。
类别可以填充任何内容。 您可以选择哺乳动物类别，其中包括所有产生牛奶的毛茸茸的温血动物。 或者，您可以创建数学对象的类别：集，几何形状或数字系统。
类别是具有附加元数据的集合：对一个对象与另一个对象进行匹配的所有方式的描述，其中包括对所有特征的描述，通过这些特征，两个对象可以被视为等同。 类别也可以想象成几何对象，其中类别的每个元素都由点表示。
想象一下，例如，一个球的表面。 该表面上的每个点都可以指示其三角形的类型。 点之间的路径表示对象之间的等价关系。 从类别理论的角度来看，我们忘记了描述一个对象的特定方式，而是将注意力集中在该对象相对于该类型的所有其他对象所占的位置上。
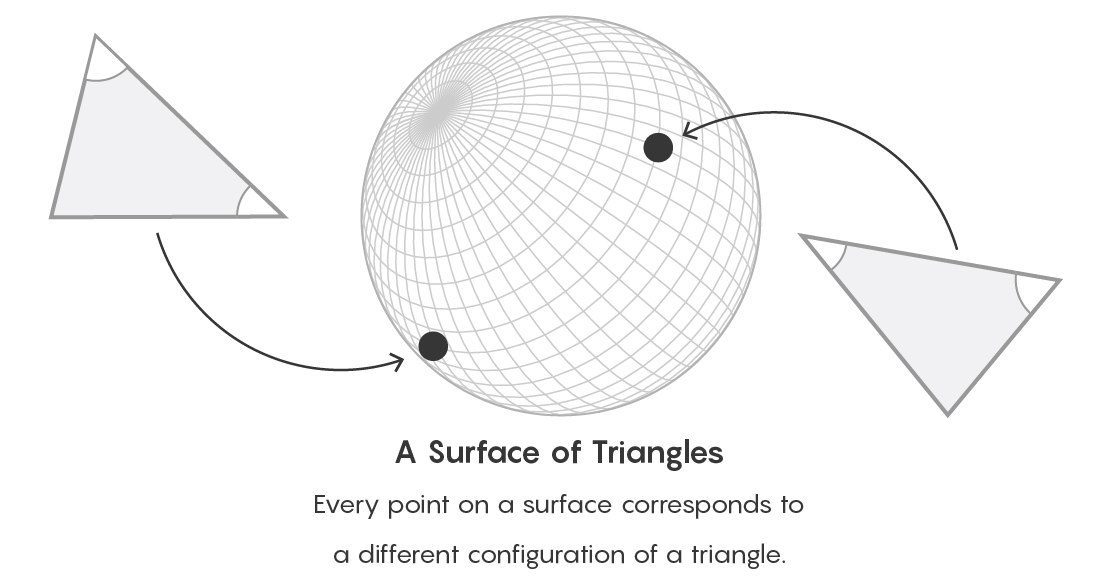表面上的每个点都对应于特定类型的三角形。“我们将许多事物视为事物，尽管实际上它们是事物之间的关系，”扎卡列维奇说。 -“我的丈夫”一词的意思是我们认为一个物体，但您可以将其视为一种关系。 其中的一部分取决于与我的关系。”
Eilenberg和MacLane的类别版本非常适合使用强大的对等选项。 但是在20世纪下半叶，数学家越来越多地使用较弱的等价形式，例如同伦。 约翰·霍普金斯大学的数学家艾米丽·瑞尔（Emily Riel）说：“数学变得越来越微妙，我们不可避免地希望对普通事物有更微妙的想法。” 在这些更好的等效形式中，有关两个对象之间的关系的信息量急剧增加。 Eilenberg和MacLane的基本类别不打算用于此目的。
要看到信息量的增加，请首先记住我们的球体，它表示不同的三角形。 如果可以通过拉伸或其他变形将一个三角形转换为另一个三角形，则两个三角形在同位素上是等价的。 如果存在将它们连接的路径，则表面上的两个点是同位的。 通过研究表面上各点之间的同位路径，您实际上正在研究这些点所表示的三角形相互连接的不同方式。
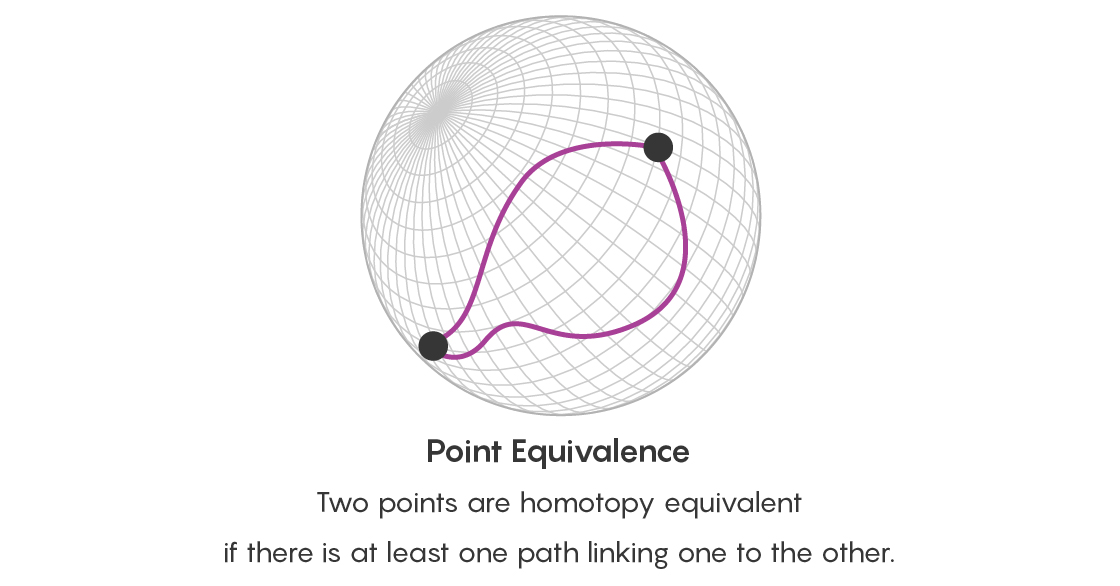
但是，仅仅声明两个点以许多等效方式连接是不够的。 还必须考虑所有这些路径的等效性。 因此，除了点的等价问题之外，现在您还要问两条在相同点处开始和结束的路径的等价问题，并且是否存在连接这些路径的路径。 连接路径的路径采用磁盘的形式，其边界是其中两个路径。
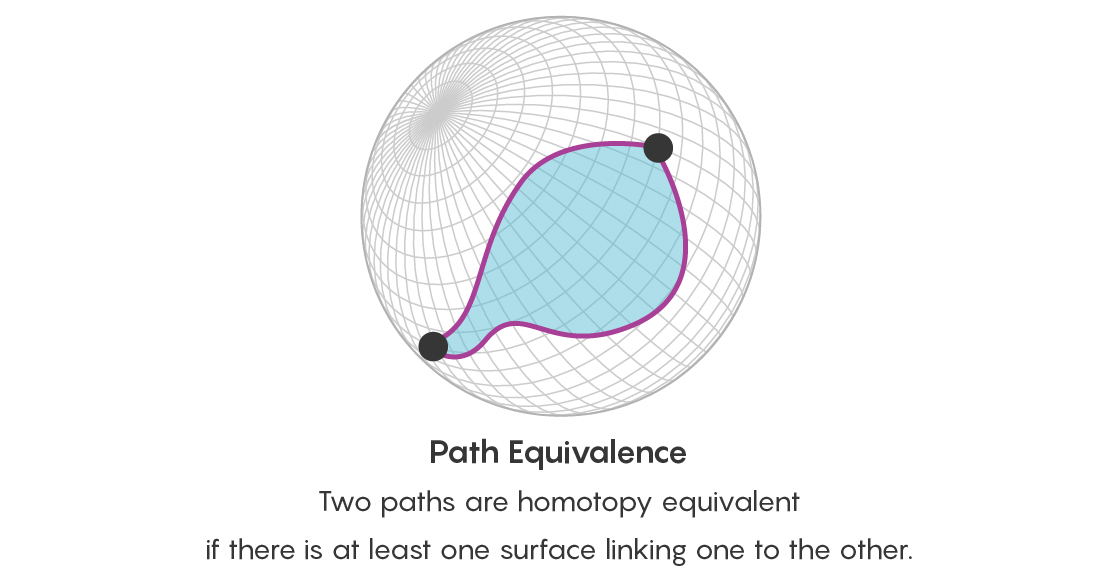
您可以进一步发展这个想法。 如果两个磁盘通过路径连接，则它们是等效的-此路径将采用三维对象的形式。 这样的三维对象本身可以通过四维路径连接（两个对象之间的路径始终比对象本身具有一维的尺寸）。
结果，您在等价之间建立了一个无限的等价塔。 关于整个理论，您将生成所有您在球体上标有点的对象的概图。
“这只是一个球体，但事实证明，要理解球体的形状，您需要以某种方式进入无穷大，”德克萨斯大学奥斯汀分校的
David Ben-Zvi说。
在20世纪的最后几十年中，许多数学家研究了“无限类”的理论-研究了什么能够追踪等价之间的无限等价塔。 其中一些取得了重大成功。 但是只有一个到达终点。
重写数学
雅各布·卢里（Jacob Lurie）在无穷大类中的第一部作品不是很成功。 2003年6月5日，这位25岁的科学家在科学预印本arxiv.org网站上发表了长达60页的题为“
无限的论点 ”的文件。 在那里，他开始草拟规则的粗略草稿，以使数学家可以处理无限大的类别。
并非每个人都以同样的方式接受第一份工作。 读完后不久，芝加哥大学的数学家
彼得·梅 （
Peter May）写信给卢瑞（Lurie）的主管迈克尔·霍普金斯（Michael Hopkins），尽管卢瑞的作品包含有趣的想法，但它看起来还没有完成，需要一种更有纪律的方法。
梅说：“我向迈克解释了我们的评论，然后他将其传递给了雅各布。”
卢瑞（Lurie）是否接受梅（May）的来信作为挑战，或者他是否已经计划了下一步（卢瑞拒绝了许多面试要求），这一点仍然未知。 显然，在收到批评意见后，Lurie经历了多年的生产力，后来成为传奇。
梅说：“我无法进入雅各布的大脑，因此我不知道他当时在想什么。” “但是我们所审查的草案与最终版本之间存在巨大差异，而最终版本已经处于完全不同的数学水平上。”
2006年，Lurie在arxiv.org上发布了“最高Topos理论”草案。 在这项艰巨的工作中，他创造了必要的设备，以无穷大的范畴为基础，用新的数学基础取代了集合论。 伊利诺伊大学厄本那-香槟分校的数学家查尔斯·雷兹克（Charles Rezk）说：“他创造了我们现在都在使用的这种基本仪器的数千页，”他在早期开发无限类别方面做了重要工作。 “我无法想象在一生中有可能创造出像'最高主题理论'这样的作品，而他是在两到三年内创造出来的。”
然后在2011年，Lurie给了另一个甚至更长的工作。 在其中，他重塑了代数。
代数为我们提供了一套很好的形式来处理方程式。 数学家不断使用这些规则来证明定理。 但是，代数在等号的固定棒上进行体操。 删除这些限制条，将其替换为更短暂的等同概念，某些操作将变得非常复杂。
采取孩子在学校学习的第一代数规则之一：联想性。 三个或更多数字的总和或乘积不取决于它们的分组：2×（3×4）=（2×3）×4。
如果使用相等性，很容易证明三个或三个以上数字的列表的关联性。 即使使用强等效性的概念进行工作，也很难做到这一点。 但是，当您继续使用更细微的等价形式时，用无尽的路径塔连接这些路径，即使是类似于关联性的简单规则，也会变成一片漆黑的森林。
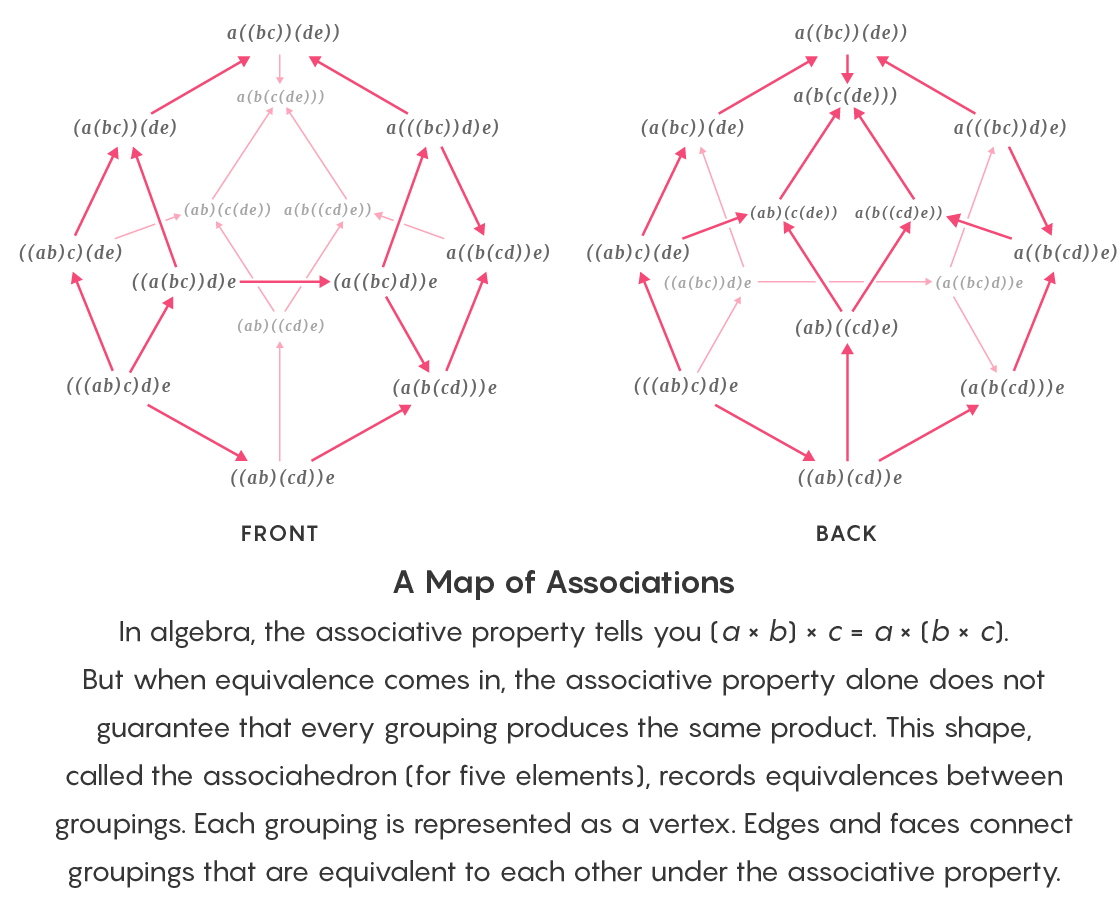在代数中，关联性表示（a×b）×c = a×（b×c）。 但是，通过使用等价关系，单独的关联性并不能保证任何元素分组都会产生相同的乘法结果。 该副二十面体包含组等效记录。 每个顶点对应一个分组。 边缘和面将彼此相关联的组组合在一起。蒙大拿大学的数学家戴维·伊斯拉（David Isla）表示：“这使问题变得极为复杂，无法使用这种新版本的数学。”
在最新的《高等代数》中，卢里（Lurie）的最新版本长达1553页，它为无穷大类以及许多其他代数定理共同构成了等价数学的基础，开发了一种关联性选项。
这两本书产生了炸弹爆炸的效果。 这样的工作引起了科学革命。 “规模非常大，” Reel说。 “这是代数几何中
格洛腾迪克水平的成就。”
但是，革命需要时间，而且，正如卢瑞（Lurie）的著作出版后所发现的那样，这些年可能是混乱的。
消化牛
数学家被认为是具有明确思维的人：证明要么正确，要么不正确。 这个想法要么行得通，要么行不通。 但是，数学家也是普通人，他们对新思想的反应与普通人相同：主观，情感上，具有个人动机。
坎贝尔说：“我认为许多关于数学家的文章都以这样的语气写着，他们正在寻找一个晶莹剔透的真理。” “但是这没有发生。” 这些人有自己的品味和舒适区，出于审美或个人原因，他们可以拒绝自己不喜欢的事物。”
在这方面，Lurie的工作已成为社区的一项复杂挑战。 实际上，这很具有启发性：这是一种新的更好的数学方法。 此信息特别针对数学家，他们全职致力于开发Lurie擅长的方法。
弗朗西斯说：“人们并不总是希望看到下一代重写他们的工作，而这个过程会产生压力。” “这是无穷大类别理论的特征之一-以前的大多数作品都与之相对应。”
由于其他原因，Lurie的作品难以消化。 大量的材料意味着数学家将不得不花费数年时间阅读他的书。 处于职业生涯中的繁忙数学家几乎是不可能提出要求的，而对于只有几年才能给出结果以使他们能够找到工作的研究生来说，这是非常冒险的。
即使与所有高级数学研究的极其抽象的性质相比，Lurie的作品也非常抽象。 并不是每个人都喜欢它。 坎贝尔说：“许多人认为卢里的作品是抽象的垃圾，许多人只是爱上了她。” “有中间选择，包括根本不了解她的人。”
艾米丽卷轴科学界一直在感知新思想，但是通常这会缓慢进行，并且每个人都在同一时间移动。 新想法的出现给社区的知识分子带来了困难。 坎贝尔说：“许多新事物马上浮出水面，就像是蟒蛇在试图消化一头牛。” “大量群众通过社区。”
如果您是一位数学家，并且相信Lurie的方法是进行数学的最佳方法，那么您的前进道路将是孤独的。 很少有人会阅读Lurie的著作，没有教科书来简短地讲述它们，也没有研讨会来帮助您掌握方向。 麻省理工学院的研究生彼得·海涅（Peter Heine）说，“只有一种方法可以对所有这些细节进行详细研究，坐下来自己做所有事情。”他花了一年的时间阅读卢里的著作。 -我认为这是最困难的。 “坐下来，自己弄清楚是不容易的，也就是说，坐下来自己阅读800页的《 Topos理论》。”
像许多新发明一样，更高理论的理论要求数学家与设备进行积极互动，从而使其发挥作用。
这样，每个梦every以求的驾驶执照的16岁男孩都将首先学习如何整理发动机。与卢里一起工作的哈佛大学数学家丹尼斯·盖茨古里（Dennis Gatesgory）说：“如果有所有这些版本的友好版本，那么该理论将立即对更广泛的数学界变得更加容易理解。”当人们开始阅读Lurie的作品并在研究中使用无穷大类别时，出现了其他问题。数学家根据无穷大类别建立了他们的工作。杂志审稿人收到这些论文并问：这是什么？巴维克说：“在某些情况下，要么是从杂志上拿出荒谬的评论，要么是完全看不懂，要么是出版了好几年。” “这可能会带来很多不便，因为在您的网站上存在多年的未发布作品看起来越来越荒谬。”但是，最大的问题不是未出版的作品，而是使用无穷大且已出版的类别的作品-但包含错误。Lurie的书是有关无穷大类别的唯一权威信息来源。它们很严格，但是很难完全理解它们。而且它们特别不适合可以被参考的指令的作用-很难搜索某些定理，或者很难验证某人在他人作品中遇到的无穷大类别的某种应用确实有效。“在该领域工作的大多数数学家都没有系统地阅读Lurie，” Andre Joyal说是蒙特利尔魁北克大学的数学家，他的早期工作是卢里（Lurie）书中的重要组成部分。 “这需要大量时间和精力，因此我们只假设他书中写的所有内容都是真实的-因为几乎每次我们检查某项内容时，它都是真实的。实际上，每次。”卢瑞（Lurie）的书籍难以获得，导致随后的一些研究不准确。 Lurie的书很难阅读，难以引用，也很难用来测试他人的作品。扎卡列维奇说：“有关无穷大类别的一般文献似乎很混乱。”尽管有形式主义，数学也不应该是只有牧师才能阅读的神圣文本。在这一领域，不仅需要大量的书籍，而且还需要小册子，不仅是最初的启示，还包括对它们的描述的解释。同时，无穷类别的理论在很大程度上以书架上几本大书的形式存在。“您可以采取这种方法。'雅各布会告诉您该怎么做，一切都井井有条，”雷兹克说。“或者您可以决定'我们不知道如何足够好地介绍我们的主题，以便人们可以使用它。”但是，很少有数学家能够接受挑战并将“无穷大”这一类别作为一项技术，供其研究领域的更多人使用。用户友好理论
为了将无限性类别转化为能够进行实际数学运算的对象，Lurie必须证明与它们相关的定理。为此，他必须选择一个景观来创建证据-就像从事几何学的人一样，有必要选择工作坐标系。数学家称此为模型选择。卢瑞（Lurie）在拟范畴模型上发展了无限性的范畴。他之前的其他数学家在其他模型上建立了无限性的类别。尽管他们的工作不像Lurie那样全面，但在某些情况下更容易与他们打交道。 Zakharevich说：“雅各布选择了一个模型，并检查了其中的所有功能，但通常并非最简单。”在几何学中，数学家清楚地了解如何在不同的坐标系之间移动。他们还证明了在某些条件下证明定理在其他条件下有效。对于无穷大类别，不存在此类保证。但是，当数学家使用无限性类别编写作品时，他们通常会轻松地在模型之间切换，从而建议（但不能证明）结果的可移植性。海涅说：“人们没有指定他们在做什么，他们在所有这些不同的模型之间切换，他们说：嗯，是同一回事。” “但这不是证明。”在过去的六年中，一些数学家试图获得这些保证。瑞尔和多米尼克来自澳大利亚McUyra大学的研究人员开发了一种描述无限性类别的方法，以克服以前使用某些模型的平台中出现的困难。他们基于巴维克和其他人的先前著作的工作证明，无论使用哪种模型，高等定理理论的许多定理仍然成立。他们用一种适当的方式证明了这种兼容性：“我们研究无穷大的类别，其对象本身就是无穷大的类别，” Ril说。 “类别理论无所适从。”Ril和Verity希望以另一种方式发展无限性类别的理论。他们选择适用于理论的方面，而不管模型如何。这样的表示形式独立于模型，具有便捷的即时适用性，他们希望这将吸引数学家进入这一研究领域，而当唯一的输入是“ High Topos Theory”时，他们便远离该领域。霍普金斯说：“进入这个世界，你需要克服护城河。” “他们这样做是为了降低桥梁。”Ryl和Verity计划明年完成工作。同时，Lurie最近开始了Kerodon项目的工作。，他计划将其转变为一本有关最高类别理论的参考书，类似于Wikipedia。在Topos理论正式化等价数学13年之后，这些举措试图完善和传播这些思想，以使等价数学更容易获得。Zhoyal说：“天才在数学的发展中起着重要作用，但是知识本身是整个社区工作的结果。” “知识的真正目标是成为整个社区的知识，而不是属于一两个人。”