马在钻头上移动。 国际象棋位板

下午好 我为 OTUS中的“开发人员算法”课程的学生特别写了这篇文章，今天我想与我们博客的所有读者分享。

一匹棋马站在棋盘上，若有所思地看着棋盘。
他可以采取几种不同的动作？



赞扬国际象棋的发明者，棋盘上有64个单元格。
赞扬计算机架构师-ulong类型也有64位。
这种巧合必须发生！
这个好主意表明了自己-将整个电路板存储为一个整数 ！ 该解决方案甚至有一个特殊术语-位板-位板。

那么，如何利用这个想法快速找到棋马的移动次数呢？

给定： knightNr-马所在板的单元格编号（从0到63）。
这是必需的： movesCount-它可以去的字段数（从2到8）。

演算法

1.将马笼号转换为ulong-位板的值
knightNr- > knightBits

2.设置所有可能动作的位
knightBits- > movesBits

3.计算单位位数
actionsBits- > moveCount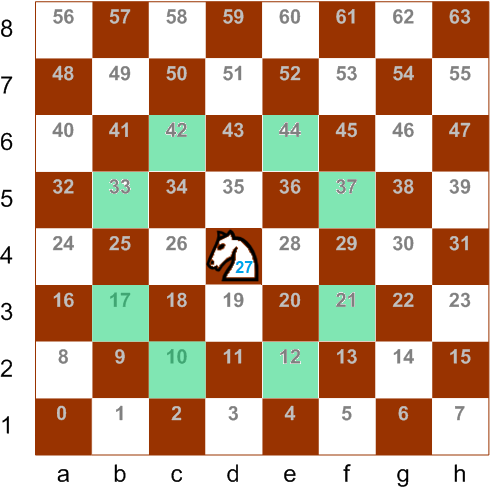



第一步非常简单，您需要将零位向左移动指定的位置数。

ulong knightBits = 1 << knightNr; 

第二步比较复杂。 一匹马可以沿着8个不同方向行驶。 我们将考虑这些偏移不是“水平/垂直”，而是位位置。 也就是说，我们考虑了每次移动需要多少个位置来移动起始位。 然后，我们使用逻辑“或”运算将所有内容“相加”。

让我们开始列出从棋盘左侧到右侧的移动：

  movesBits = knightBits << 6 | knightBits >> 10 //  b5  b3 | knightBits << 15 | knightBits >> 17 //  c6  c2 | knightBits << 17 | knightBits >> 15 //  e6  e2 | knightBits << 10 | knightBits >> 6 //  f5  f3; 

是的，很酷！

不幸的是，板的边缘有“黑洞”。 例如，根据此算法，您可以从单元格a4（位＃24）到达单元格g2（位＃14 = 24-10），此跳跃是将球形国际象棋马在真空中通过黑洞传送到极端垂直区域 ...

为了排除马在板边缘上的量子跃迁，必须在移动后“断开”极端带。 例如，对于移动6和-10（向左移动两个单元格），必须取消在g和h垂直方向上获得的值，因为在向左“移动”两次移动后您无法在这些垂直方向上结束。

为此，我们需要4位网格常数，其中所有位都设置为1（指示的垂直除外）。 即：

  ulong nA = 0xFeFeFeFeFeFeFeFe; ulong nAB = 0xFcFcFcFcFcFcFcFc; ulong nH = 0x7f7f7f7f7f7f7f7f; ulong nGH = 0x3f3f3f3f3f3f3f3f; 

在棋盘的顶部和底部也有“黑洞”，可以完全吸收马匹，因此不需要单独检查它们。

现在，用于生成允许的马步运动的算法如下所示：

  movesBits = nGH & (knightBits << 6 | knightBits >> 10) | nH & (knightBits << 15 | knightBits >> 17) | nA & (knightBits << 17 | knightBits >> 15) | nAB & (knightBits << 10 | knightBits >> 6); 

它的运行速度非常快（！）。

一点点滴答-我们有了所有可能的马术冒险的位图。 最令人惊讶的是，即使板上有几匹马，该算法也能正常工作。 他立刻为所有马匹产生所有可能的动作！ 是的，太好了！

仍然需要计算位数

最简单的方法是将数字右移1位并计数。 难度-64次操作。 内存-64位。

最快的方法是创建一个包含65536个元素的缓存/数组，其中每个索引的位数从0到65535。将这个数组中的4个元素添加到对应于该数字的下一个16位段的元素。
难度-4次操作。 内存-64 KB。

但是我们将考虑最棘手的方法 ，其复杂度等于数字中单个位的数量。 由于移动不多，因此这种方法对我们而言是最佳的。

首先，我们注意到，通过从数字中减去一个单位，我们将所有“正确的”零变成单位，而最外面的单位变成零：

 1001010100010000 - 1 = 1001010100001111 

接下来，对这些数字应用逻辑“和”运算：

 1001010100010000 & 1001010100001111 = 1001010100000000 

如您所见，我们以一种棘手的方式将最右边的单位重置为零。 重复此操作，直到结果为零。 多少次迭代，那么多单个位。 是的，太好了！

这是完整编写此算法的方式：

  int movesCount = 0; while (movesBits != 0) { movesBits &= (movesBits - 1); movesCount ++; } 

问题解决了！

此任务还有另一个非常简单的纯粹逻辑上的解决方案：确定骑士到棋盘边缘的距离（在角落有2步，在边缘附近有3到6步，在中心有8步）。 但是，如果我们要以这种方式解决“正面问题”，我们将不会了解位板，垂直位掩码，快速计数单个位的算法以及真空中球形马的黑洞……

现在我们知道了一切。 国际象棋程序员的生活变得更加丰富和有意义，欢呼！

自己动手 做 ： 为国际象棋王做同样的事情。