本文的翻译是专门为机器学习课程的学生准备的。
加强培训带动了人工智能的发展。 从AlphaGo和
AlphaStar开始，基于增强训练的AI代理现在已经征服了越来越多的人类主导的活动。 简而言之，这些成就取决于在特定环境中优化代理的行为以实现最大的回报。 在
GradientCrescent的最后几篇文章中
，我们研究了强化学习的各个基本方面，从
强盗系统的基础知识和基于
策略的方法到在
马尔可夫环境中优化基于奖励的行为。 所有这些方法都需要完全了解我们的环境。 例如，
动态编程要求我们具有所有可能状态转换的完整概率分布。 但是，实际上，我们发现大多数系统无法完全解释，并且由于复杂性，内在的不确定性或计算能力的限制，无法明确获得概率分布。 打个比方，考虑一下气象学家的任务-天气预报涉及的因素数量如此之多，以致无法准确计算出概率。
对于这种情况，可以采用诸如蒙特卡洛的教学方法。 术语“蒙特卡洛”通常用于描述随机抽样估计的任何方法。 换句话说，我们不会预测有关环境的知识，而是会通过与环境互动而获得的示例性状态，动作和奖励序列来从经验中学习。 这些方法的工作原理是直接观察模型在正常运行期间返回的报酬，以判断其条件的平均值。 有趣的是，即使没有任何关于环境动态的知识（应该将其视为状态转换的概率分布），我们仍然可以获得最佳行为来最大化回报。
例如，考虑掷出12个骰子的结果。 将这些抛出视为单个状态，我们可以将这些结果取平均值，以便更接近真实的预测结果。 样本越大，我们越能准确地接近实际预期结果。
60击12骰子的平均预期数量为41.57对于读者来说，这种基于采样的评估似乎很熟悉，因为这种采样也是针对k-bandit系统执行的。 而不是比较不同的匪徒，而是使用蒙特卡洛方法在马尔可夫环境中比较不同的策略，在遵循特定策略之前确定状态的值，直到工作完成。
状态值的蒙特卡洛估计
在强化学习的背景下，蒙特卡洛方法是一种通过平均样本结果来评估模型状态的重要性的方法。 由于需要终端状态，因此蒙特卡洛方法固有地适用于情节环境。 由于此限制，通常将蒙特卡洛方法视为“自主”方法，其中所有更新均在达到终端状态后执行。 可以给出一个简单的类比方法，即找到迷宫的出路-自主的方法将迫使特工到达最后，然后利用获得的中间经验来尝试减少穿越迷宫的时间。 另一方面，通过联机方法，代理将在迷宫通过期间就已经不断改变其行为，也许他会注意到绿色走廊导致死角，例如决定避开它们。 我们将在以下文章之一中讨论在线方法。
蒙特卡洛方法可以表述为：
为了更好地了解蒙特卡洛方法的工作原理，请考虑下面的状态转换图。 每个状态转换的奖励都以黑色显示，折扣系数为0.5。 让我们抛开状态的实际值，专注于计算一掷的结果。
状态转换图。 状态编号显示为红色，结果为黑色。假定终端状态返回的结果等于0，让我们从终端状态（G5）开始计算每个状态的结果。 请注意，我们已将折现系数设置为0.5，这将导致对以后各州的加权。
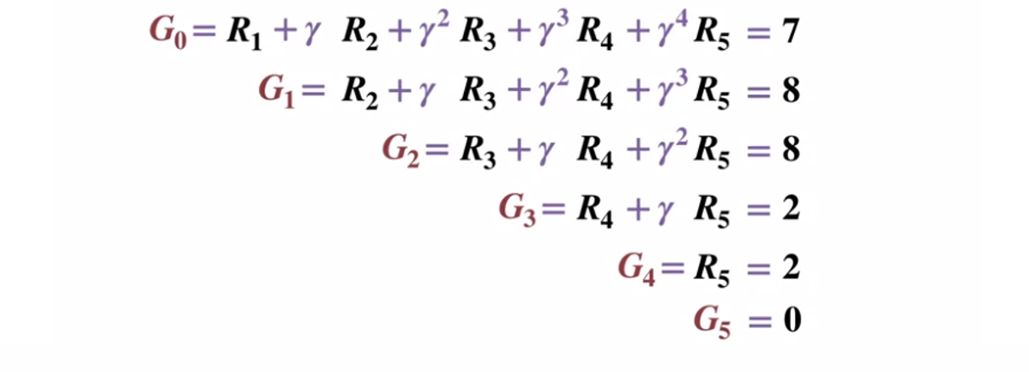
或更笼统地说：
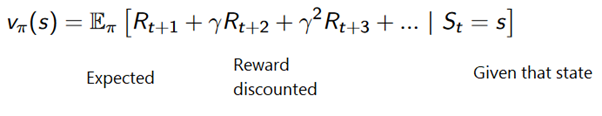
为了避免将所有结果存储在列表中，我们可以使用与传统梯度下降方法有些相似的方程式，在蒙特卡洛方法中逐步执行更新状态值的过程：
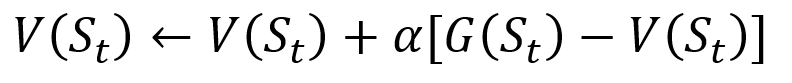蒙特卡洛增量更新过程。 S是状态，V是其值，G是其结果，A是阶跃值参数。作为强化培训的一部分，蒙特卡洛方法甚至可以分为首次访问或每次访问。 简而言之，两者之间的区别在于在一次蒙特卡洛更新之前，一个段落可以访问多少次状态。 蒙特卡洛首次访问方法将所有状态的值评估为完成访问之前对每个州的单次访问后结果的平均值，而蒙特卡洛每次访问方法对n次访问到完成为止的结果进行平均。 由于本文相对简单，因此我们将在本文中使用“蒙特卡洛首次访问”。
蒙特卡洛政策管理
如果模型无法提供策略，则可以使用Monte Carlo评估状态行为值。 这不仅仅是状态的意义，因为在给定状态下每个动作
（q）的含义的思想使代理能够根据陌生环境中的观察结果自动生成策略。
更正式地讲，我们可以使用蒙特卡洛方法来估计
q（s，a，pi） ，即从状态s，操作a和后续策略
Pi开始的预期结果。 蒙特卡洛方法保持不变，不同之处在于对特定状态采取的其他措施。 可以认为，如果曾经访问过状态
s并在其中执行了操作
a，则在通过过程中会访问一个状态
（s，a）对。 同样，可以使用“首次访问”和“每次访问”方法对价值行为进行评估。
与动态编程一样，我们可以使用广义迭代策略（GPI）通过观察状态操作值来形成策略。
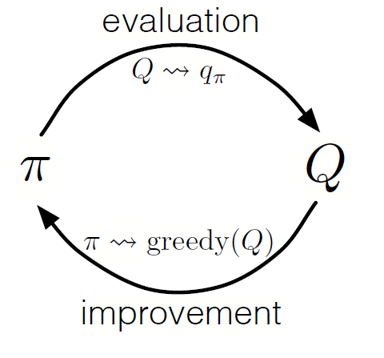
通过交替执行政策评估和政策改进的步骤，并包括进行研究以确保所有可能的措施都得到访问，我们可以针对每种情况实现最佳政策。 对于蒙特卡洛GPI，此轮换通常在每次通过结束后进行。
蒙特卡洛GPI二十一点策略
为了更好地了解蒙特卡洛方法在评估各种状态值的任务中的实际工作方式，让我们逐步演示二十一点游戏示例。 首先，让我们确定游戏的规则和条件：
- 我们只会与庄家对抗，不会再有其他玩家。 这将使我们能够将经销商的手中考虑为环境的一部分。
- 号码等于标称值的卡的价值。 图片卡的值：Jack，King和Queen是10。根据玩家的选择，王牌的值可以是1或11。
- 双方收到两张卡。 两张玩家牌面朝上，庄家的一张牌也面朝上。
- 游戏的目标是手中的纸牌数量少于或等于21张。 大于21的值表示破产，如果双方的值均为21，则游戏以平局方式进行。
- 在玩家看到自己的卡和第一张庄家的卡之后，玩家可以选择是否要带他一张新卡（“足够”）（“足够”），直到他对手中的卡总和感到满意为止。
- 然后发牌者出示他的第二张卡-如果结果少于17张，则他必须拿起卡，直到达到17分为止，此后他不再拿卡。
让我们看看蒙特卡洛方法如何与这些规则一起工作。
第一轮
您总共获得19分。但是，您尝试抓住尾巴的运气，抓住机会，获得3分并破产。 当您破产时，发牌人只有一张未结清牌，总数为10。这可以表示如下：
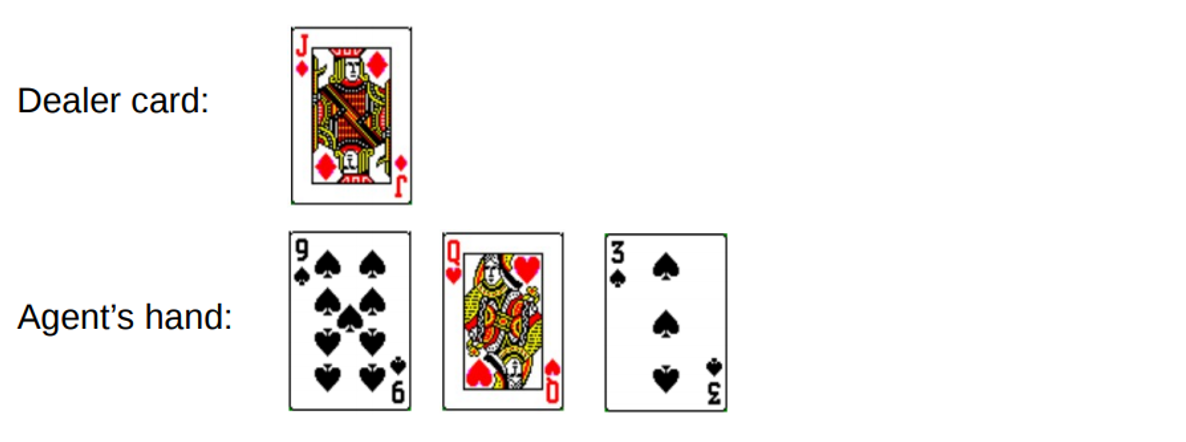
如果我们破产了，则本轮奖励为-1。 让我们使用以下格式[代理商数量，经销商数量，ace？]将此值设置为倒数第二个状态的返回结果：
好吧，现在我们运气不好了。 让我们继续下一轮。
第二回合
您总共键入19。这一次您决定停止。 发牌者拨13，拿卡，然后摔坏。 倒数第二个状态可以描述如下。
让我们描述一下本轮获得的条件和奖励：
在本文的结尾，我们现在可以使用计算的结果来更新本轮所有状态的值。 采取1的折扣系数，我们只需分配新手奖励，就像之前的状态转换一样。 由于状态
V（19，10，no）先前返回-1，因此我们计算期望的返回值并将其分配给我们的状态：
以二十一点为例进行演示的最终状态值 。
实作
让我们使用首次访问的蒙特卡洛方法编写二十一点游戏，以使用Python找出游戏中所有可能的状态值（或手头的各种组合）。 我们的方法将基于
Sudharsan等人的
方法。 等 。 和往常一样，您可以在
GitHub上的文章中找到所有代码。
为了简化实施，我们将使用OpenAI的Gym。 将环境视为以最少的代码启动二十一点的接口，这将使我们能够专注于实施强化学习。 方便地，所有有关状态，动作和奖励的收集信息都存储在
“观察”变量中，这些变量在当前游戏会话期间累积。
让我们首先导入获取和收集结果所需的所有库。
import gym import numpy as np from matplotlib import pyplot import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D from collections import defaultdict from functools import partial %matplotlib inline plt.style.use('ggplot')
接下来，让我们初始化我们的
体育馆环境并定义一个策略，该策略将协调我们代理的动作。 实际上，我们将继续拿卡，直到手中的金额达到19或更多，然后我们停止。
让我们定义一种使用我们的策略生成通过数据的方法。 我们将存储有关状态，采取的措施以及该措施的报酬的信息。
def generate_episode(policy, env):
最后，让我们定义“蒙特卡洛”预测函数的首次访问。 首先，我们初始化一个空字典来存储当前状态值，并初始化一个字典来存储不同状态中每个状态的记录数。
def first_visit_mc_prediction(policy, env, n_episodes):
对于每次通过，我们调用
generate_episode方法来获取有关状态值和状态发生后获得的奖励的信息。 我们还初始化变量以存储增量结果。 然后，我们获得通过期间访问的每个州的奖励和当前状态值，并通过每步奖励的值来增加变量回报。
for _ in range(n_episodes):
让我提醒您，由于我们正在实施蒙特卡洛的首次访问，因此我们将一次性访问一个州。 因此，我们对状态字典进行条件检查，以查看状态是否已被访问。 如果满足此条件，则我们能够使用先前定义的过程来计算新值，以使用蒙特卡洛方法更新状态值，并将对该状态的观察数增加1。然后，我们对下一个遍历重复该过程，以便最终获得结果的平均值。
让我们运行我们得到的，看看结果！
value = first_visit_mc_prediction(sample_policy, env, n_episodes=500000) for i in range(10): print(value.popitem())
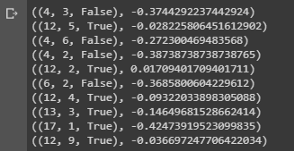显示二十一点中手上各种组合的状态值的样本结论。我们可以继续对5000次传球进行蒙特卡洛观察，并建立状态值分布，以描述玩家和发牌手手中任何组合的值。
def plot_blackjack(V, ax1, ax2): player_sum = np.arange(12, 21 + 1) dealer_show = np.arange(1, 10 + 1) usable_ace = np.array([False, True]) state_values = np.zeros((len(player_sum), len(dealer_show), len(usable_ace))) for i, player in enumerate(player_sum): for j, dealer in enumerate(dealer_show): for k, ace in enumerate(usable_ace): state_values[i, j, k] = V[player, dealer, ace] X, Y = np.meshgrid(player_sum, dealer_show) ax1.plot_wireframe(X, Y, state_values[:, :, 0]) ax2.plot_wireframe(X, Y, state_values[:, :, 1]) for ax in ax1, ax2: ax.set_zlim(-1, 1) ax.set_ylabel('player sum') ax.set_xlabel('dealer sum') ax.set_zlabel('state-value') fig, axes = pyplot.subplots(nrows=2, figsize=(5, 8),subplot_kw={'projection': '3d'}) axes[0].set_title('state-value distribution w/o usable ace') axes[1].set_title('state-value distribution w/ usable ace') plot_blackjack(value, axes[0], axes[1])
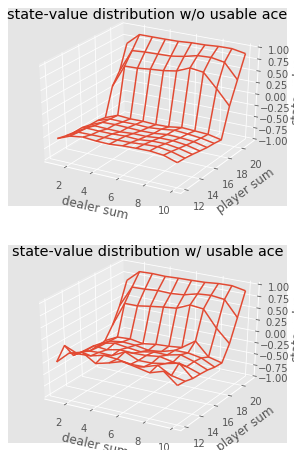二十一点中各种组合的状态值的可视化。因此，让我们总结一下我们学到了什么。
- 基于采样的学习方法使我们能够简单地通过采样来评估状态和动作状态值，而没有任何过渡动态。
- 蒙特卡洛方法基于模型的随机抽样，观察模型返回的报酬，并在正常运行期间收集信息以确定其状态的平均值。
- 使用蒙特卡洛方法，可以使用广义的迭代策略。
- 二十一点游戏者和庄家手中所有可能组合的值可以使用多个蒙特卡洛模拟进行估算，从而为优化策略铺平了道路。
到此结束对蒙特卡洛方法的介绍。 在我们的下一篇文章中，我们将继续学习“时差学习”形式的教学方法。
资料来源：
萨顿等 al，强化学习
白等。 al，艾伯塔大学强化学习基础
席尔瓦（Silva）等。 al，强化学习，UCL
普拉特等 东北大学铝仅此而已。 在
课程中见！