我继续发表我的演讲，最初是为那些学习“数字地质”专业的学生而准备的。 这是该中心出版的第三本出版物，第一篇是介绍性文章，无需阅读。 但是，要理解本文，有必要阅读线性方程组的介绍 ，即使您知道它是什么，因为我将大量参考该介绍中的示例。

因此，今天的任务是：学习最简单的几何处理，例如，能够将我的头变成复活节岛的偶像：



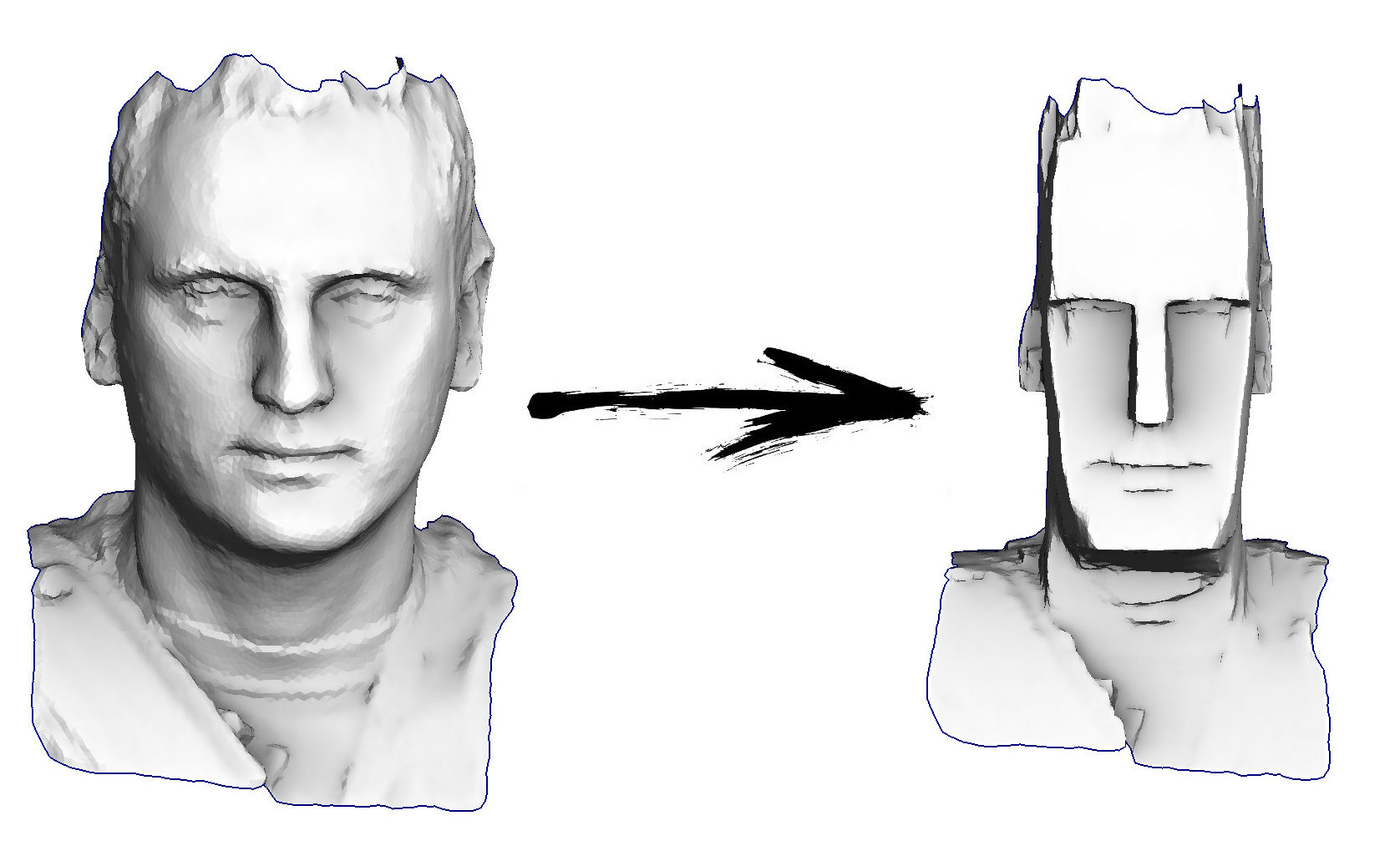
当前的演讲计划：

• 概率论教育程序（入门文章，可选）
  
• 线性方程组介绍
  
• 最小化二次形式和OLS问题的示例
  
• 从最小二乘到神经网络
  

官方课程资料库位于此处 。 这本书还没有读完，我正在慢慢地编辑哈布雷出版的文章。

在本文中，我的主要工具将是寻找最小二次函数； 但是在我们开始使用此工具之前，您至少需要了解他在哪里拥有“打开/关闭”按钮。 首先，刷新内存，然后回忆一下什么是矩阵，什么是正数以及什么是导数。

矩阵和数字

在本文中，我将大量使用矩阵表示法，因此让我们回顾一下它是什么。 不要在文本中进一步看，要暂停几秒钟，然后尝试公式化什么是矩阵。

不同的矩阵解释

答案很简单。 矩阵只是一个存放辣根的柜子。 每个狗屎都位于其单元格中，单元格按行和列按行分组。 在我们的特殊情况下，通常的实数是废话； 对于程序员而言，最容易呈现矩阵 $$喜欢的东西

float A[m][n]; 

为什么需要这种存储？ 他们描述什么？ 也许我会让你不高兴，但是矩阵本身并没有描述任何东西，它存储着。 例如，您可以在其中存储任何函数的系数。 让我们忘记矩阵一秒钟，然后想象我们有一个数字 $$$一$ 。 什么意思 是的，魔鬼知道...例如，它可能是函数内部的一个系数，该系数以一个数字作为输入，并以另一个数字作为输出：

$$

$$f（x）：\ mathbb R \ rightarrow \ mathbb R$$

数学家可以写这样一个函数的一个版本：

$$

$$f（x）=斧$$

好吧，在程序员的世界里，它看起来像这样：

 float f(float x) { return a*x; } 

另一方面，为什么要这样的功能，而又不完全是另一个？ 让我们再来一个！

$$

$$f（x）=斧^ 2$$

自从我开始学习程序员以来，我必须写她的代码:)

 float f(float x) { return x*a*x; } 

这些函数之一是线性的，第二个函数是二次的。 哪一个是正确的？ 不，数字本身 $$$一$ 没有定义它，只是存储了一些价值！ 您需要什么功能，像这样构建一个。

矩阵也会发生同样的事情，如果没有足够的单个数字（标量），这是数字的一种扩展，这些就是需要的存储。 就像在数字上一样，在矩阵上方也定义了加法和乘法运算。

假设我们有一个矩阵 $$例如，尺寸为2x2：

$$

$$A = \开始{bmatrix} a_ {11}和a_ {12} \\ a_ {21}＆a_ {22} \结束{bmatrix}$$

这个矩阵本身并不意味着任何东西，例如，它可以解释为一个函数

$$

$$f（x）：\ mathbb R ^ 2 \ rightarrow \ mathbb R ^ 2，\ quad f（x）= Ax$$

 vector<float> f(vector<float> x) { return vector<float>{a11*x[0] + a12*x[1], a21*x[0] + a22*x[1]}; } 

此函数将二维向量转换为二维向量。 在图形上，将其表示为图像转换很方便：我们将图像提供给输入，在输出处得到其拉伸和/或旋转（甚至可以镜像！）版本。 很快我将给出带有矩阵解释的各种示例的图片。

并且可以矩阵 $$想象一下将二维向量转换为标量的函数：

$$

$$f（x）：\ mathbb R ^ 2 \ rightarrow \ mathbb R，\ quad f（x）= x ^ \ top A x = \ sum \ limits_i \ sum \ limits_j a_ {ij} x_i x_j$$

请注意，矢量的乘幂不是很明确，所以我不能写 $$$x ^ 2$ ，就像他在写普通数字时一样。 我强烈建议那些不习惯处理矩阵乘法的人，再次回忆一下矩阵乘法规则，并验证表达式 $$$x ^ \ top A x$ 通常允许，并且确实在出口处给出了标量。 为此，例如，您可以明确地放在方括号中 $$$x ^ \ top A x =（x ^ \ top A）x$ 。 我提醒你，我们有 $$$x$ 是维度2的向量（存储在维度2x1的矩阵中），我们明确编写所有维度：

$$

$$\ underbrace {\ underbrace {\ left（\ underbrace {x ^ \ top} _ {1 \ times 2} \ times \ underbrace {A} _ {2 \ times 2} \ right）} _ {1 \ times 2} \ times \ underbrace {x} _ {2 \ times 1}} _ {1 \ times 1}$$

回到温暖蓬松的程序员世界，我们可以编写相同的二次函数，如下所示：

 float f(vector<float> x) { return x[0]*a11*x[0] + x[0]*a12*x[1] + x[1]*a21*x[0] + x[1]*a22*x[1]; } 

什么是正数？

现在我将问一个非常愚蠢的问题：什么是正数？ 我们有了一个称为谓词的强大工具 $$$>$ 。 但是花点时间回答这个数字 $$$一$ 当且仅当 $$$a> 0$ 那太容易了。 让我们定义正性如下：

定义1

编号 $$$一$ 当且仅当对于所有非零实数为正 $$$x \ in \ mathbb R，\ x \ neq 0$ 条件满足 $$$ax ^ 2> 0$ 。

它看起来很棘手，但它完全适用于矩阵：

定义2

方阵 $$如果为非零，则称为正定 $$$x$ 条件满足 $$$x ^ \ top A x> 0$ 也就是说，除了原点外，其他所有地方的对应二次形式都严格为正。

为什么我需要积极性？ 正如我在文章开头提到的那样，我的主要工具将是搜索二次函数的最小值。 但是至少要进行搜索，如果它存在的话也不错！ 例如一个功能 $$$f（x）=-x ^ 2$ 因为数字-1不是正数，所以最小值显然不存在，并且 $$$f（x）$ 随着增长而不断减少 $$$x$ ：抛物线的分支 $$$f（x）$ 往下看 正定矩阵是好的，因为相应的二次形式形成了具有（唯一）最小值的抛物面。 下图显示了七个不同的矩阵示例。 $$$2 \乘2$ ，无论是正定的还是对称的，事实并非如此。 上排：矩阵作为函数的解释 $$$f（x）：\ mathbb R ^ 2 \ rightarrow \ mathbb R ^ 2$ 。 中排：将矩阵解释为函数 $$$f（x）：\ mathbb R ^ 2 \ rightarrow \ mathbb R$ 。



因此，我将使用正定矩阵，它们是正数的推广。 而且，在我的情况下，矩阵也将对称！ 很好奇的是，当人们谈论积极确定性时，它们也常常意味着对称，而对称性可以通过以下观察（可以理解以下文字）来间接解释。

二次形式矩阵对称性的抒情离题

让我们看一下二次形式 $$$x ^ \前M x$ 对于任意矩阵 $$$M$ ; 然后 $$$M$ 添加并立即减去其转置版本的一半：

$$

$$M = \底线{\ frac {1} {2}（M + M ^ \ top）} _ {：= M_s} + \底线{\ frac {1} {2}（MM ^ \ top）} _ { ：= M_a} = M_s + M_a$$

矩阵 $$$M_s$ 对称的： $$$M_s ^ \ top = M_s$ ; 矩阵 $$$M_a$ 反对称： $$$M_a ^ \ top = -M_a$ 。 一个显着的事实是，对于任何反对称矩阵，对应的二次形式都等于零。 这来自以下观察：

$$

$$q = x ^ \ top M_a x =（x ^ \ top M_a ^ \ top x）^ \ top =-（x ^ \ top M_a x）^ \ top = -q$$

也就是说，二次形式 $$$x ^ \ top M_a x$ 同时等于 $$$q$ 和 $$$-q$ ，仅当 $$$q \等于0$ 。 从这个事实可以得出，对于任意矩阵 $$$M$ 对应的二次形式 $$$x ^ \前M x$ 可以通过对称矩阵表示 $$$M_s$ ：

$$

$$x ^ \ top M x = x ^ \ top（M_s + M_a）x = x ^ \ top M_s x + x ^ \ top M_a x = x ^ \ top M_s x。$$

我们正在寻找二次函数的最小值

让我们简短地回到一维世界。 我想找到最少的功能 $$$f（x）=斧^ 2-2bx$ 。 编号 $$$一$ 肯定地，因此存在一个最小值； 为了找到它，我们将相应的导数等于零： $$$\ frac {d} {dx} f（x）= 0$ 。 区分劳动的一维二次函数不是： $$$\ frac {d} {dx} f（x）= 2ax-2b = 0$ ; 所以我们的问题归结为求解方程式 $$$ax-b = 0$ ，通过艰苦的努力，我们找到了解决方案 $$$x ^ * = b / a$ 。 下图说明了两个问题的等效性：解决方案 $$$x ^ *$ 方程式 $$$ax-b = 0$ 与方程的解一致 $$$\ mathrm {argmin} _x（ax ^ 2-2bx）$ 。



我倾向于这样一个事实，即我们的总体目标是最小化二次函数，但是我们正在谈论最小二乘。 但是与此同时，我们真正知道如何做得很好的是求解线性方程（以及线性方程组）。 而且一个等于另一个很酷！

给我们留下的唯一一件事就是确保一维世界中的等价性扩展到案例 $$$n$ 变量。 为了验证这一点，我们首先证明三个定理。

三个定理或微分矩阵表达式

第一个定理指出矩阵 $$$1 \乘以1$ 关于换位的不变式：

定理1

$$$x \ in \ mathbb R \ Rightarrow x ^ \ top = x$

证明太复杂了，为了简洁起见，我不得不省略它，但是请尝试自己找到它。

第二定理使我们能够区分线性函数。 对于一个变量的实函数，我们知道 $$$\ frac {d} {dx}（bx）= b$ 但是在实函数的情况下会发生什么 $$$n$ 变量？

定理2

$$$\ nabla b ^ \ top x = \ nabla x ^ \ top b = b$

也就是说，不出意外，只是记录同一学校成绩的矩阵记录。 证明非常简单，只需编写渐变的定义即可：

$$

$$\ nabla（b ^ \ top x）= \开始{bmatrix} \ frac {\部分（b ^ \ top x）} {\部分x_1} \\ \ vdots \\ \ frac {\部分（b ^ \ top x）} {\部分x_n} \结束{bmatrix} = \开始{bmatrix} \ frac {\部分（b_1 x_1 + \点+ b_n x_n）} {\部分x_1} \\ \ vdots \\ \ frac {\部分（b_1 x_1 + \点+ b_n x_n）} {\部分x_n} \结束{bmatrix} = \开始{bmatrix} b_1 \\ \ vdots \\ b_n \结束{bmatrix} = b$$

应用第一个定理 $$$b ^ \ top x = x ^ \ top b$ ，我们完成了证明。

现在我们传递给二次形式。 我们知道在一个变量的实函数的情况下 $$$\ frac {d} {dx}（ax ^ 2）= 2ax$ ，并且在二次形式的情况下会发生什么？

定理3

$$$\ nabla（x ^ \ top A x）=（A + A ^ \ top）x$

顺便提一下，如果矩阵 $$对称，那么定理说 $$$\ nabla（x ^ \ top A x）= 2Ax$ 。

该证明也很简单，只需将二次形式写为双倍和：

$$

$$x ^ \ top A x = \ sum \ limits_i \ sum \ limits_j a_ {ij} x_i x_j$$

然后，让我们看看这个双重和关于变量的偏导数是什么 $$$x_i$ ：
\开始{align *}
\ frac {\部分（x ^ \ top A x）} {\部分x_i}
＆= \ frac {\部分} {\部分x_i} \左（\ sum \极限_ {k_1} \ sum \极限_ {k_2} a_ {k_1 k_2} x_ {k_1} x_ {k_2} \右）= \\
＆= \ frac {\部分} {\部分x_i} \左（
\ underbrace {\ sum \ limit_ {k_1 \ neq i} \ sum \ limits_ {k_2 \ neq i} a_ {ik_2} x_ {k_1} x_ {k_2}} _ _ {k_1 \ neq i，k_2 \ neq i} + \底线{\ sum \ limits_ {k_2 \ neq i} a_ {ik_2} x_i x_ {k_2}} _ {k_1 = i，k_2 \ neq i} +
\ underbrace {\ sum \ limits_ {k_1 \ neq i} a_ {k_1 i} x_ {k_1} x_i} _ {k_1 \ neq i，k_2 = i} +
\ underbrace {a_ {ii} x_i ^ 2} _ {k_1 = i，k_2 = i} \ right）= \\
＆= \ sum \ limits_ {k_2 \ neq i} a_ {ik_2} x_ {k_2} + \ sum \ limits_ {k_1 \ neq i} a_ {k_1 i} x_ {k_1} + 2 a_ {ii} x_i = \\
＆= \ sum \ limits_ {k_2} a_ {ik_2} x_ {k_2} + \ sum \ limits_ {k_1} a_ {k_1 i} x_ {k_1} = \\
＆= \ sum \ limits_ {j}（a_ {ij} + a_ {ji}）x_j \\
\结束{align *}
我将双和分为四个案例，以大括号突出显示。 这四种情况均微不足道。 它仍然要做最后的动作，收集梯度向量中的偏导数：

$$

$$\ nabla（x ^ \ top A x）= \开始{bmatrix} \ frac {\部分（x ^ \ top Ax）} {\部分x_1} \\ \ vdots \\ \ frac {\部分（x ^ \顶部A x）} {\部分x_n} \结束{bmatrix} = \开始{bmatrix} \和\ limit_ {j}（a_ {1j} + a_ {j1}）x_j \\ \ vdots \\ \ sum \ limits_ {j}（a_ {nj} + a_ {jn}）x_j \ end {bmatrix} =（A + A ^ \ top）x$$

二次函数的最小值和线性系统的解

让我们不要忘记旅行的方向。 我们看到一个正数 $$$一$ 对于一个变量的实函数，求解方程 $$$ax = b$ 或最小化二次函数 $$$\ mathrm {argmin} _x（ax ^ 2-2bx）$ 是一回事。

我们想在对称正定矩阵的情况下显示相应的连接 $$。
所以我们想找到二次函数的最小值

$$

$$\ mathrm {argmin} _ {x \ in \ mathbb R ^ n}（x ^ \ top A x-2b ^ \ top x）$$

就像在学校一样，我们将导数等于零：

$$

$$\ nabla（x ^ \ top A x-2b ^ \ top x）= \开始{bmatrix} 0 \\ \ vdots \\ 0 \ end {bmatrix}$$

Hamilton算子是线性的，因此我们可以按以下形式重写方程式：

$$

$$\ nabla（x ^ \ top A x）-2 \ nabla（b ^ \ top x）= \开始{bmatrix} 0 \\ \ vdots \\ 0 \ end {bmatrix}$$

现在我们应用第二和第三阶微分定理：

$$

$$（A + A ^ \ top）x-2b = \开头{bmatrix} 0 \\ \ vdots \\ 0 \结束{bmatrix}$$

回想一下 $$对称，并将方程分为两部分，我们得到所需的线性方程组：

$$

$$斧= b$$

Hooray从一个变量变为多个变量，我们什么都没有丢失，并且我们可以有效地最小化二次函数！

我们传递到最小二乘

最后，我们可以继续本讲座的主要内容。 想象一下，我们在飞机上有两个点 $$$（x_1，y_1）$ 和 $$$（x_2，y_2）$ ，我们想找到穿过这两个点的直线方程。 这条线的方程可以写成 $$$y = \ alpha x + \ beta$ ，也就是说，我们的任务是找到系数 $$$\ alpha$ 和 $$$\ beta$ 。 此练习是针对该学校的七年级学生，我们写下了方程组：

$$

$$\左\ {\开始{拆分} \ alpha x_1 + \ beta＆= y_1 \\ \ alpha x_2 + \ beta＆= y_2 \\ \结束{split} \ right。$$

我们有两个带有两个未知数的方程（ $$$\ alpha$ 和 $$$\ beta$ ），其余的都是已知的。

在一般情况下，解决方案是存在的并且是唯一的。 为了方便起见，我们以矩阵形式重写相同的系统：

$$

$$\ underbrace {\ begin {bmatrix} x_1＆1 \\ x_2＆1 \ end {bmatrix}} _ {：= A} \ underbrace {\ begin {bmatrix} \ alpha \\ \ beta \ end {bmatrix}} _ {：= x} = \底线{\开始{bmatrix} y_1 \\ y_2 \结束{bmatrix}} _ {：= b}$$

我们得到一个类型的方程 $$$斧= b$ 琐碎地解决了 $$$x ^ * = A ^ {-1} b$ 。

现在想象一下，我们有三个点需要画一条直线：

$$

$$\左\ {\开始{拆分} \ alpha x_1 + \ beta＆= y_1 \\ \ alpha x_2 + \ beta＆= y_2 \\ \ alpha x_3 + \ beta＆= y_3 \\ \结束{split} \ right 。$$

该系统以矩阵形式编写如下：

$$

$$\ underbrace {\ begin {bmatrix} x_1＆1 \\ x_2＆1 \\ x_3＆1 \ end {bmatrix}} _ {：= A \，（3 \ 2倍）} \ underbrace {\ begin {bmatrix} \ alpha \\ \ beta \ end {bmatrix}} _ {：= x \，（2 \ times 1）} = \底线{\开始{bmatrix} y_1 \\ y_2 \\ y_3 \ end {bmatrix}} _ { ：= b \，（3 \乘以1）}$$

现在我们有了一个矩阵 $$矩形，它根本不存在反向！ 这是完全正常的，因为我们只有两个变量和三个方程，在一般情况下，该系统没有解。 这是现实世界中的一种完全正常的情况，当这些点是来自噪声测量的数据时，我们需要找到参数 $$$\ alpha$ 和 $$$\ beta$ 最接近的测量数据。 在第一个演讲中，当我们对杆秤进行校准时，我们已经考虑了这个示例。 但是那时我们的解决方案纯粹是代数的，非常麻烦。 让我们尝试一种更直观的方法。

我们的系统可以编写如下：

$$

$$\ alpha \ underbrace {\开始{bmatrix} x_1 \\ x_2 \\ x_3 \ end {bmatrix}} _ {：= \ vec {i}} + \ beta \ underbrace {\开始{bmatrix} 1 \\ 1 \ \ 1 \结束{bmatrix}} _ {：= \ vec {j}} = \开始{bmatrix} y_1 \\ y_2 \\ y_3 \结束{bmatrix}$$

或者，更简单地说，

$$

$$\ alpha \ vec {i} + \ beta \ vec {j} = \ vec {b}。$$

向量 $$$\ vec我$ ， $$$\ vec j$ 和 $$$\ vec b$ 已知，需要找到标量 $$$\ alpha$ 和 $$$\ beta$ 。
显然是线性组合 $$$\ alpha \ vec {i} + \ beta \ vec {j}$ 产生一架飞机，如果向量 $$$\ vec b$ 不在这个平面上，那么就没有确切的解决方案； 但是，我们正在寻找一种近似的解决方案。

让我们将决策错误定义为 $$$\ vec {e}（\ alpha，\ beta）：= \ alpha \ vec {i} + \ beta \ vec {j}-\ vec b$ 。 我们的目标是找到这样的参数值 $$$\ alpha$ 和 $$$\ beta$ 最小化向量的长度 $$$\ vec {e}（\ alpha，\ beta）$ 。 换句话说，问题写为 $$$\ mathrm {argmin} _ {\ alpha，\ beta} \ | \ vec {e}（\ alpha，\ beta）\ |$ 。
这是一个例证：



给定向量 $$$\ vec我$ ， $$$\ vec j$ 和 $$$\ vec b$ ，我们尝试最小化误差向量的长度 $$$\ vec e$ 。 显然，如果它的长度垂直于在矢量上拉伸的平面，则其长度将最小化 $$$\ vec我$ 和 $$$\ vec j$ 。

但是，等等，最小的平方在哪里？ 现在他们会的。 根提取功能 $$$\ sqrt {\ cdot}$ 因此单调 $$$\ mathrm {argmin} _ {\ alpha，\ beta} \ | \ vec {e}（\ alpha，\ beta）\ |$ = $$$\ mathrm {argmin} _ {\ alpha，\ beta} \ | \ vec {e}（\ alpha，\ beta）\ | ^ 2$ ！

很明显，如果误差向量的长度垂直于在向量上延伸的平面，则它的长度将最小化 $$$\ vec我$ 和 $$$\ vec j$ ，可以通过将对应的标量乘积等于零来编写：

$$

$$\左\ {\开始{分割} \ vec {i} ^ \ top \ vec {e}（\ alpha，\ beta）＆= 0 \\ \ vec {j} ^ \ top \ vec {e}（\ alpha，\ beta）＆= 0 \ end {split} \ right。$$

以矩阵形式，该同一系统可以写成

$$

$$\开始{bmatrix} x_1＆x_2＆x_3 \\ 1＆1＆1 \结束{bmatrix} \向左（\ alpha \开始{bmatrix} x_1 \\ x_2 \\ x_3 \结束{bmatrix} + \ beta \开始{bmatrix} 1 \\ 1 \\ 1 \结束{bmatrix}-\开始{bmatrix} y_1 \\ y_2 \\ y_3 \ end {bmatrix} \ right）= \开始{bmatrix} 0 \\ 0 \ end {bmatrix }$$

否则

$$

$$\开始{bmatrix} x_1＆x_2＆x_3 \\ 1＆1＆1 \结束{bmatrix} \向左（\开始{bmatrix} x_1＆1 \\ x_2＆1 \\ x_3＆1 \结束{bmatrix} \开始{bmatrix} \ alpha \\ \ beta \结束{bmatrix}-\开始{bmatrix} y_1 \\ y_2 \\ y_3 \结束{bmatrix} \ right）= \开始{bmatrix} 0 \\ 0 \结束{bmatrix }$$

但是我们不会止步于此，因为可以进一步减少记录：

$$

$$A ^ \ top（Ax-b）= \开始{bmatrix} 0 \\ 0 \ end {bmatrix}$$

最近的转换：

$$

$$A ^ \ top Ax = A ^ \ top b。$$

让我们计算尺寸。 矩阵 $$有大小 $$$3 \乘2$ 因此 $$$A ^ \ top A$ 有大小 $$$2 \乘2$ 。 矩阵 $$$b$ 有大小 $$$3 \乘1$ 但是矢量 $$$A ^ \ top b$ 有大小 $$$2 \乘以1$ 。 也就是说，在一般情况下，矩阵 $$$A ^ \ top A$ 可逆的！ 而且， $$$A ^ \ top A$ 它具有几个不错的属性。

定理4

$$$A ^ \ top A$ 对称的。

这一点一点都不难显示：

$$

$$（A ^ \ top A）^ \ top = A ^ \ top（A ^ \ top）^ \ top = A ^ \ top A.$$

定理5

$$$A ^ \ top A$ 正半定： $$$\ forall x \ in \ mathbb R ^ n \ quad x ^ \ top A ^ \ top A x \ geq 0$

这是由于以下事实： $$$x ^ \ top A ^ \ top A x =（A x）^ \ top A x> 0$ 。

也 $$$A ^ \ top A$ 正定如果 $$具有线性独立的列（排名 $$等于系统中的变量数）。

总之，对于具有两个未知数的系统，我们证明了二次函数的最小化 $$$\ mathrm {argmin} _ {\ alpha，\ beta} \ | \ vec {e}（\ alpha，\ beta）\ | ^ 2$ 等效于求解线性方程组 $$$A ^ \ top A x = A ^ \ top b$ 。 当然，所有这些推理都适用于任何其他数量的变量，但让我们使用简单的代数计算将所有内容再次紧凑地写在一起。 我们从最小二乘问题开始，对熟悉形式的二次函数进行最小化，然后得出结论，这等效于求解线性方程组。 因此，我们开始：

$$

$$\开始{拆分} \ Mathrm {argmin} \ | Ax-b \ | ^ 2＆= \ mathrm {argmin}（Ax-b）^ \ top（Ax-b）= \\＆= \ mathrm {argmin}（x ^ \ top A ^ \ top-b ^ \ top）（Ax-b）= \\＆= \ mathrm {argmin}（x ^ \ top A ^ \ top A x-b ^ \ top Ax-x ^ \ top A ^ \ top b + \ underbrace {b ^ \ top b} _ {\ rm const}）= \\＆= \ mathrm {argmin}（x ^ \ top A ^ \ top A x-2b ^ \ top Ax）= \\＆= \ mathrm {argmin}（ x ^ \ top \ underbrace {（A ^ \ top A）} _ {：= A'} x-2 \ underbrace {{A ^ \ top b）} _ {：= b'} \ phantom {} ^ \ top x）\结束{拆分}$$

所以最小二乘问题 $$$\ mathrm {argmin} \ |斧头-b \ | ^ 2$ 等效于最小化二次函数 $$$\ mathrm {argmin}（x ^ \ top A'x-2b'^ \ top x）$ （一般情况下）有一个对称的正定矩阵 $$$A'$ ，又相当于求解线性方程组 $$$A'x = b'$ 。 ff 理论已经结束。

让我们继续练习

示例一，一维

让我们回想一下上一篇文章中的一个示例：

 # initialize the data array x = [0.] * 32 x[0] = x[31] = 1. x[18] = 2. # smooth the array values other than at indices 0,18,31 for iter in range(1000): for i in range(len(x)): if i in [0,18,31]: continue x[i] = (x[i-1] + x[i+1])/2. 

我们有32个元素的常规x数组，其初始化如下：



然后，我们将执行以下过程一千次：对于每个单元x [i]，我们将邻近单元的平均值写入其中：x [i] =（x [i-1] + x [i + 1]）/ 2。 唯一的例外：我们不会用数字0、18和31重写数组的元素。这就是数组在前一百五十次迭代中的样子：



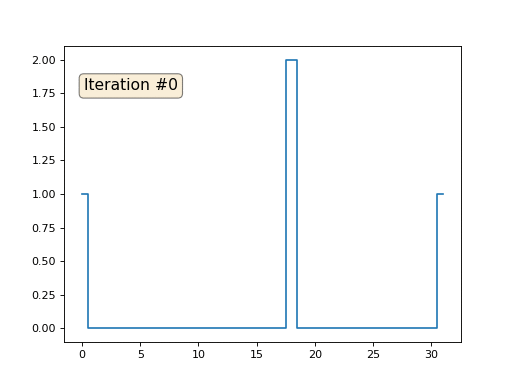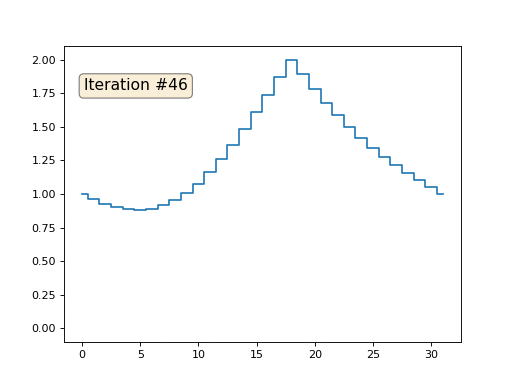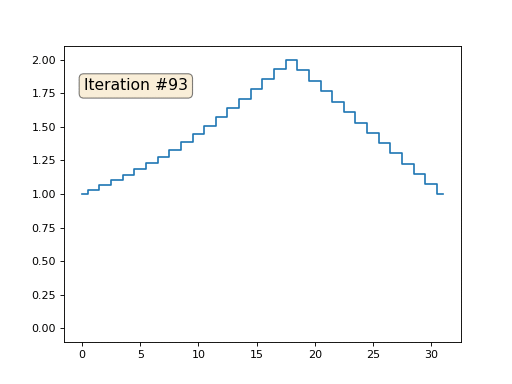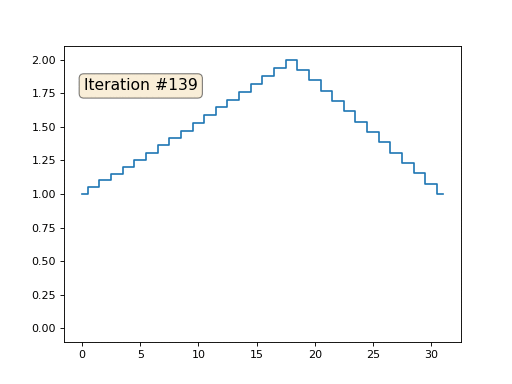
正如我们在前一篇文章中发现的那样 ，事实证明，我们的四行python代码宏代码通过Gauss-Seidel方法解决了以下线性方程组：



他们发现了，但是这个系统是从哪里来的呢？ 什么样的魔术？ 让我们离题，尝试解决稍微不同的系统。 我仍然有32个变量，但是现在我希望它们全都相等。 写下这个并不难，写下一个方程式系统就足够了，该方程式指出所有相邻元素成对相等：



上面的Python代码原则上不会触及三个变量的值：x0，x18，x31，因此让我们将它们传递到方程组的右侧，即从未知数集中排除：



我固定初始值x0 = 1，第一个方程式说x1 = x0 = 1，第二个方程式说x2 = x1 = x0 = 1依此类推，直到我们得到方程式1 = x0 = x17 = x18 = 2哦 但是这个系统没有解决方案：（（

不管，我们是程序员！ 让我们叫最小平方来寻求帮助！ 我们无法解决的系统可以用矩阵形式编写 $$$斧= b$ ; 大概解决我们的系统，就足以解决系统 $$$A^\top Ax=A^\top b$ 。然后事实证明，这正是上一篇文章中的一对一方程组！

凭直觉，可以想象创建系统矩阵的过程，如下所示：我们通过弹簧连接要实现其相等性的值。例如，在我们的情况下，我们想要$$X 我是等于$x_i$$$x i + 1，所以我们加上等式$x_{i+1}$$$x i - x i + 1 = 0，在这些值之间悬挂一个弹簧，将它们拉在一起。但是，由于x0，x18和x31的值是固定不变的，因此除了均匀拉伸弹簧之外，没有其他任何自由值，从而产生（在这种情况下）分段线性解决方案。让我们编写一个解决该方程组的程序。在上一篇文章中，我们看到Gauss-Seidel方法的编程非常简单，但是收敛速度很慢，因此最好使用线性方程组的实数求解器。在最简单的情况下，对于我们的一维示例，代码可能看起来像这样：$x_i - x_{i+1}=0$

 import numpy as np n = 32 # size of the vector to produce # fill the matrix with 2nd order finite differences A = np.matrix(np.zeros((n-1, n))) for i in range(0,n-1): A[i, i] = -1. A[i, i+1] = 1. # eliminate the constrained variables from the matrix A = A[:,[*range(1,18)] + [*range(19,31)]] b = np.matrix(np.zeros((n-1, 1))) b[0,0] = 1. b[17,0] = -2. b[18,0] = 2. b[n-2,0] = -1. # solve the system x = np.linalg.inv(A.transpose()*A)*A.transpose()*b x = x.transpose().tolist()[0] # re-introduce the constrained variables x.insert(0, 1.) x.insert(18, 2.) x.append(1.) 

该代码产生一个x的32个元素的列表，其中存储了解决方案。我们正在建立一个矩阵$$ 建筑矢量 $$b，我们得到一个带有解的向量$b$$$X = （甲⊤甲）- 1甲⊤ b，然后插入到该载体中提供了固定的值x0 = 1，X18 = X31 = 2和1。这段代码可以完成必要的工作，但是将固定变量的值传递到右侧是非常不愉快的。有可能作弊吗？可以！让我们看下面的代码：$x = (A^\top A)^{-1}A^\top b$

 import numpy as np n = 32 # size of the vector to produce # fill the matrix with 2nd order finite differences A = np.matrix(np.zeros((n-1+3, n))) for i in range(0,n-1): A[i, i] = -1. A[i, i+1] = 1. # enforce the constraints through the quadratic penalty A[n-1+0, 0] = 100. A[n-1+1,18] = 100. A[n-1+2,31] = 100. b = np.matrix(np.zeros((n-1+3, 1))) b[n-1+0,0] = 100.*1. b[n-1+1,0] = 100.*2. b[n-1+2,0] = 100.*1. # solve the system x = np.linalg.inv(A.transpose()*A)*A.transpose()*b x = x.transpose().tolist()[0] 

从程序员的角度来看，这要好得多，可以立即获得所需尺寸的向量x，并且可以更轻松地填充矩阵A和b。但是，诀窍是什么？让我们来写一个求解的方程组：



仔细查看最后三个方程：
100 x0 = 100 *
1100 x18 = 100 * 2
100 x31 = 100 * 1

编写它们的方法是否容易如下？
x0 = 1
x18 = 2
x31 = 1

不，不容易。正如我已经说过的，每个方程式都悬挂着弹簧，在这种情况下，x0和值1之间的弹簧，x18和值2之间的弹簧，最后，变量x31也将被吸引。

但是存在100的系数是有原因的。我们记得这个系统只是无法求解，我们从最小二乘的意义上解决了它，从而最小化了相应的二次函数。将最后三个方程式的每个系数乘以100，我们引入了将x0，x18和x32偏离期望值的惩罚，超过了偏离等式的惩罚的一万倍（100 ^ 2）$$$x_i = x_{i+1}$ 。粗略地讲，后三个方程的弹簧比其他所有方程都难上万倍。这种二次惩罚方法是引入限制的非常方便的工具；比减少一组变量要简单得多（尽管并非没有缺点）。

实例二，三维

让我们继续进行一些比平滑一维数组的元素更有趣的事情！首先，我们将做完全一样的工作，但要使用更多有趣的数据和实际工具。我想获取一个三维曲面，固定其边界，并尽可能使曲面的其余部分平滑：此处提供了



代码，以防万一我将给出主文件的完整列表：

 #include <vector> #include <iostream> #include "OpenNL_psm.h" #include "geometry.h" #include "model.h" int main(int argc, char** argv) { if (argc<2) { std::cerr << "Usage: " << argv[0] << " obj/model.obj" << std::endl; return 1; } Model m(argv[1]); for (int d=0; d<3; d++) { // solve for x, y and z separately nlNewContext(); nlSolverParameteri(NL_NB_VARIABLES, m.nverts()); nlSolverParameteri(NL_LEAST_SQUARES, NL_TRUE); nlBegin(NL_SYSTEM); nlBegin(NL_MATRIX); for (int i=0; i<m.nhalfedges(); i++) { // fix the boundary vertices if (m.opp(i)!=-1) continue; int v = m.from(i); nlRowScaling(100.); nlBegin(NL_ROW); nlCoefficient(v, 1); nlRightHandSide(m.point(v)[d]); nlEnd(NL_ROW); } for (int i=0; i<m.nhalfedges(); i++) { // smooth the interior if (m.opp(i)==-1) continue; int v1 = m.from(i); int v2 = m.to(i); nlRowScaling(1.); nlBegin(NL_ROW); nlCoefficient(v1, 1); nlCoefficient(v2, -1); nlEnd(NL_ROW); } nlEnd(NL_MATRIX); nlEnd(NL_SYSTEM); nlSolve(); for (int i=0; i<m.nverts(); i++) { m.point(i)[d] = nlGetVariable(i); } } std::cout << m; return 0; } 

我编写了wavefront .obj文件的最简单的解析器，因此该模型在一行中加载。作为求解器，我将使用OpenNL，它是解决稀疏矩阵最小二乘问题的强大求解器。请注意，矩阵的尺寸可能是巨大的：例如，如果我们要获取1000 x 1000像素的黑白图片，则矩阵$$一个⊤一个我们将有一百万的大小，以一百万！但是，实际上，此矩阵的绝大多数元素通常都是零，因此一切并不是那么可怕，但是您仍然需要使用特殊的求解器。因此，让我们看一下代码。首先，我向求解器宣布我要执行的操作：$A^\top A$

  nlNewContext(); nlSolverParameteri(NL_NB_VARIABLES, m.nverts()); nlSolverParameteri(NL_LEAST_SQUARES, NL_TRUE); nlBegin(NL_SYSTEM); nlBegin(NL_MATRIX); 

我想要一个矩阵 $$甲⊤甲大小（科尔维尔顶点）×（科尔维尔顶点）。注意，我们给求解器一个矩阵$A^\top A$$$ 和 $$一个⊤一个它会自身建设，这是非常方便！另外，请注意以下事实：我不是求解一个方程组，而是针对x，y和z串联求解三个方程组（我认为问题是三维的，但仍然是一维的！），然后逐行声明矩阵。首先，我修复曲面边缘上的顶点：$A^\top A$

  for (int i=0; i<m.nhalfedges(); i++) { // fix the boundary vertices if (m.opp(i)!=-1) continue; int v = m.from(i); nlRowScaling(100.); nlBegin(NL_ROW); nlCoefficient(v, 1); nlRightHandSide(m.point(v)[d]); nlEnd(NL_ROW); } 

您可以看到我使用100 ^ 2的平方惩罚来修复边顶点。

好吧，然后为每对相邻的顶点在它们之间悬挂一个刚度为1的弹簧：

  for (int i=0; i<m.nhalfedges(); i++) { // smooth the interior if (m.opp(i)==-1) continue; int v1 = m.from(i); int v2 = m.to(i); nlRowScaling(1.); nlBegin(NL_ROW); nlCoefficient(v1, 1); nlCoefficient(v2, -1); nlEnd(NL_ROW); } 

我们执行代码，看看如何在弯曲的线上将表面平滑到肥皂膜的表面。我们刚刚解决了Dirichlet问题，获得了面积最小的表面。

我们提升特色

让我们将自己的脸变成一个怪诞的面具：



在上一篇文章中，我已经展示了如何在膝盖上执行此操作，在这里，我给出了一个使用最小二乘法求解器的真实代码：

  for (int d=0; d<3; d++) { // solve for x, y and z separately nlNewContext(); nlSolverParameteri(NL_NB_VARIABLES, m.nverts()); nlSolverParameteri(NL_LEAST_SQUARES, NL_TRUE); nlBegin(NL_SYSTEM); nlBegin(NL_MATRIX); for (int i=0; i<m.nhalfedges(); i++) { // fix the boundary vertices if (m.opp(i)!=-1) continue; int v = m.from(i); nlRowScaling(100.); nlBegin(NL_ROW); nlCoefficient(v, 1); nlRightHandSide(m.point(v)[d]); nlEnd(NL_ROW); } for (int i=0; i<m.nhalfedges(); i++) { // light attachment to the original geometry if (m.opp(i)==-1) continue; int v1 = m.from(i); int v2 = m.to(i); nlRowScaling(.2); nlBegin(NL_ROW); nlCoefficient(v1, 1); nlCoefficient(v2, -1); nlRightHandSide(m.point(v1)[d] - m.point(v2)[d]); nlEnd(NL_ROW); } for (int v=0; v<m.nverts(); v++) { // amplify the curvature nlRowScaling(1.); nlBegin(NL_ROW); int nneigh = m.incident_halfedges(v).size(); nlCoefficient(v, nneigh); Vec3f curvature = m.point(v)*nneigh; for (int hid : m.incident_halfedges(v)) { nlCoefficient(m.to(hid), -1); curvature = curvature - m.point(m.to(hid)); } nlRightHandSide(2.5*curvature[d]); nlEnd(NL_ROW); } nlEnd(NL_MATRIX); nlEnd(NL_SYSTEM); nlSolve(); for (int i=0; i<m.nverts(); i++) { m.point(i)[d] = nlGetVariable(i); } } 

完整的代码在这里。他如何工作？与前面的示例一样，我从固定边顶点开始。然后，对于每条边缘我（安静地，系数为0.2）说，如果它的形状与原始曲面完全相同，那就太好了：

  for (int i=0; i<m.nhalfedges(); i++) { // light attachment to the original geometry if (m.opp(i)==-1) continue; int v1 = m.from(i); int v2 = m.to(i); nlRowScaling(.2); nlBegin(NL_ROW); nlCoefficient(v1, 1); nlCoefficient(v2, -1); nlRightHandSide(m.point(v1)[d] - m.point(v2)[d]); nlEnd(NL_ROW); } 

如果您什么都不做，并按原样解决问题，那么我们应该确切地了解输出的输出内容：输出边界等于输入边界，加上输出的差异等于输入的差异。

但是我们不会止步于此！

  for (int v=0; v<m.nverts(); v++) { // amplify the curvature nlRowScaling(1.); nlBegin(NL_ROW); int nneigh = m.incident_halfedges(v).size(); nlCoefficient(v, nneigh); Vec3f curvature = m.point(v)*nneigh; for (int hid : m.incident_halfedges(v)) { nlCoefficient(m.to(hid), -1); curvature = curvature - m.point(m.to(hid)); } nlRightHandSide(2.5*curvature[d]); nlEnd(NL_ROW); } 

我在系统中添加了更多方程式。对于每个顶点，我计算输入曲面中围绕它的曲面的曲率，然后将其乘以两个半，即输出曲面到处都应具有较大的曲率。

然后我们调用求解器并获得良好的讽刺画。

今天的最后一个例子

到目前为止，我们还没有看到一个新的示例，所有内容已在上一篇文章中显示。让我们尝试做一些比最简单的平滑更简单的事情，而无需使用任何求解器就可以很容易地获得它。该代码在此处可用，但让我给您列出：

 #include <vector> #include <iostream> #include "OpenNL_psm.h" #include "geometry.h" #include "model.h" const Vec3f axes[] = {Vec3f(1,0,0), Vec3f(-1,0,0), Vec3f(0,1,0), Vec3f(0,-1,0), Vec3f(0,0,1), Vec3f(0,0,-1)}; int snap(Vec3f n) { // returns the coordinate axis closest to the given normal double nmin = -2.0; int imin = -1; for (int i=0; i<6; i++) { double t = n*axes[i]; if (t>nmin) { nmin = t; imin = i; } } return imin; } int main(int argc, char** argv) { if (argc<2) { std::cerr << "Usage: " << argv[0] << " obj/model.obj" << std::endl; return 1; } Model m(argv[1]); std::vector<int> nearest_axis(m.nfaces()); for (int i=0; i<m.nfaces(); i++) { Vec3f v[3]; for (int j=0; j<3; j++) v[j] = m.point(m.vert(i, j)); Vec3f n = cross(v[1]-v[0], v[2]-v[0]).normalize(); nearest_axis[i] = snap(n); } for (int d=0; d<3; d++) { // solve for x, y and z separately nlNewContext(); nlSolverParameteri(NL_NB_VARIABLES, m.nverts()); nlSolverParameteri(NL_LEAST_SQUARES, NL_TRUE); nlBegin(NL_SYSTEM); nlBegin(NL_MATRIX); for (int i=0; i<m.nhalfedges(); i++) { int v1 = m.from(i); int v2 = m.to(i); nlRowScaling(1.); nlBegin(NL_ROW); nlCoefficient(v1, 1); nlCoefficient(v2, -1); nlRightHandSide(m.point(v1)[d] - m.point(v2)[d]); nlEnd(NL_ROW); int axis = nearest_axis[i/3]/2; if (d!=axis) continue; nlRowScaling(2.); nlBegin(NL_ROW); nlCoefficient(v1, 1); nlCoefficient(v2, -1); nlEnd(NL_ROW); } nlEnd(NL_MATRIX); nlEnd(NL_SYSTEM); nlSolve(); for (int i=0; i<m.nverts(); i++) { m.point(i)[d] = nlGetVariable(i); } } std::cout << m; return 0; } 

我们仍然在与以前一样的表面上进行工作；我们为每个三角形调用snap（）函数。该函数表示坐标系的哪个轴最接近该三角形的法线。也就是说，我们想知道这个三角形更可能是垂直或水平的。好吧，那么我们要更改表面的几何形状，以使靠近水平面的东西变得更近！该图的左侧显示了snap（）函数的结果：



因此，我们用三种颜色绘制了曲面，分别对应于坐标系的三个轴。好吧，那么对于我们系统的每个边缘，我们添加以下方程式：

  nlRowScaling(1.); nlBegin(NL_ROW); nlCoefficient(v1, 1); nlCoefficient(v2, -1); nlRightHandSide(m.point(v1)[d] - m.point(v2)[d]); nlEnd(NL_ROW); 

也就是说，我们指示输出表面的每个边缘都类似于输入表面的相应边缘，即弹簧1的刚度。然后，如果我们允许例如x尺寸，并且该边缘应垂直，那么我们简单地说一个顶点等于另一个顶点，并具有弹簧的刚度。 2：

  nlRowScaling(2.); nlBegin(NL_ROW); nlCoefficient(v1, 1); nlCoefficient(v2, -1); nlEnd(NL_ROW); 

好吧，这是我们程序的结果：一个



完全合理的问题：复活节岛的偶像当然很酷，但是地质与它有什么关系？是否有实际问题的例子？

当然可以让我们看一看地壳的一部分：



对于地质学家来说，不同岩石的层非常重要，它们之间的边界（水平）以绿色显示，而地质断层则以红色显示。我们在输入处有我们感兴趣的区域的三角形网格（3D中的四面体），但是需要四边形（3D中的六面体）对某些过程进行建模。我们对模型进行变形，以使断层变为垂直而水平（惊奇）变为水平：



然后，我们只取一个规则的正方形网格，将我们的域切成均匀的正方形，并对它们应用逆变换，以获得必要的四边形网格。

结论

最小二乘法是一种强大的数据处理工具，与Excel列中的统计信息相比，它们的使用范围广泛。由于将二次函数最小化和线性方程组求解是相同的事实，这些可能性为我们打开了大门，而且我们（人类）已经学会了非常非常好地求解线性方程组，甚至完全解决了具有数十亿个变量的非人类尺寸。

但是，有时我们可能没有足够的线性模型。例如，在这里，神经网络可以为您提供帮助。在下一篇文章中，我将尝试证明拒绝排放的OLS等效于神经网络的公式之一。保持在线！