
10月,举行了第二届编程冠军赛。 我们收到了12,500份申请,有6,000多人参加了比赛。 这次,参与者可以选择以下轨道之一:后端,前端,移动开发和机器学习。 在每个赛道中,都必须通过资格赛阶段和决赛。
按照传统,我们将发布有关哈布雷的曲目分析。 让我们从机器学习资格阶段的任务开始。 团队准备了五项这样的任务,其中三个任务有两个选择:在第一个版本中,有任务A1,B1和C,在第二个版本中有任务A2,B2和C。这些选项在参与者之间随机分配。 任务C的作者是我们的开发人员Pavel Parkhomenko,其余任务由他的同事Nikita Senderovich完成。
对于第一个简单的算法任务(A1 / A2),通过正确枚举答案,参与者可以获得50分。 对于第二项任务(B1 / B2),我们给出10至100分-取决于解决方案的有效性。 要获得100分,需要实施动态编程方法。 第三项任务致力于根据提供的训练数据构建点击模型。 它要求应用处理分类属性的方法,并使用非线性训练模型(例如,梯度增强)。 对于该任务,最多可以得到150点-取决于测试样品上损失函数的值。
A1。 恢复轮播的长度
条件
推荐系统应有效地确定人们的利益。 除了机器学习方法外,还使用特殊的界面解决方案来执行此任务,从而明确询问用户对他有什么兴趣。 一种这样的解决方案是轮播。
轮播是水平的卡条,每张卡都提供订阅特定来源或主题的功能。 轮播中可以多次找到同一张卡。 轮播可以从左向右滚动,而在最后一张卡之后,用户再次看到第一张。 对于用户而言,从最后一张卡片到第一张卡片的过渡是不可见的,从他的角度看,磁带是无止境的。
在某个时候,一个好奇的用户瓦西里(Vasily)注意到磁带实际上是在缠绕的,并决定找出转盘的真实长度。 为此,为了简化起见,他开始滚动浏览录像带并依次写出会议卡,并用小写的拉丁字母指定每个卡。 于是瓦西里在纸上写下了前n张卡片。 可以保证他至少看过所有轮播卡。 然后瓦西里上床睡觉,早晨他发现有人在便签上洒了一杯水,现在有些字母无法辨认。
根据剩余信息,帮助Vasily确定轮播中的最小数量的卡片。
I / O格式和示例输入格式
第一行包含一个整数n(1≤n≤1000)-Vasily写入的字符数。
第二行包含Vasily编写的序列。 它由n个字符组成-小写拉丁字母和#号,这意味着该位置的字母无法识别。
输出格式
打印单个整数正数-轮播中可能的最小卡数。
例子1
例子2
例子3
例子4
注意事项
在第一个示例中,所有字母都被识别,最小轮播可以包含3张卡片-abc。
在第二个示例中,所有字母都被识别,最小轮播可以包含3张卡片-abb。 请注意,该轮播中的第二张和第三张相同。
在第三个示例中,如果我们假设符号a位于第三位置,则将获得最小的轮播长度。 那么初始行是ababa,最小轮播包含2张卡片-ab。
在第四个示例中,源字符串可以是任何东西,例如ffffff。 然后,轮播可能包含一张卡片-f。
评分系统
只有通过了该任务的所有测试,您才能获得
50分 。
在测试系统中,测试1-4是条件示例。
解决方案
找出轮播的可能长度从1到n,并确定每个固定长度是否足够,就足够了。 显然,答案总是存在的,因为n的值可以保证是可能的答案。 对于固定的轮播长度p,足以验证在所有位置i,i + p,i + 2p等处从0到(p-1)的所有i的传输线中,找到相同的字符或#。 如果至少对于某些i,从a到z范围内有2个不同的字符,则轮播的长度不能为p。 由于在最坏的情况下,对于每个p,您都需要运行一次字符串的所有字符,因此该算法的复杂度为O(n
2 )。
def check_character(char, curchar): return curchar is None or char == "#" or curchar == char def need_to_assign_curchar(char, curchar): return curchar is None and char != "#" n = int(input()) s = input().strip() for p in range(1, n + 1): is_ok = True for i in range(0, p): curchar = None for j in range(i, n, p): if not check_character(s[j], curchar): is_ok = False break if need_to_assign_curchar(s[j], curchar): curchar = s[j] if not is_ok: break if is_ok: print(p) break
A2。 恢复轮播的长度
条件
推荐系统应有效地确定人们的利益。 除了机器学习方法外,还使用特殊的界面解决方案来执行此任务,从而明确询问用户对他有什么兴趣。 一种这样的解决方案是轮播。
轮播是水平的卡条,每张卡都提供订阅特定来源或主题的功能。 轮播中可以多次找到同一张卡。 轮播可以从左向右滚动,而在最后一张卡之后,用户再次看到第一张。 对于用户而言,从最后一张卡片到第一张卡片的过渡是不可见的,从他的角度看,磁带是无止境的。
在某个时候,一个好奇的用户瓦西里(Vasily)注意到磁带实际上是在缠绕的,并决定找出圆盘传送带的真实长度。 为此,为了简化起见,他开始滚动浏览录像带并依次写出会议卡,并用小写的拉丁字母指定每个卡。 因此,瓦西里(Vasily)写下了前n张卡片。 可以保证他至少看过所有轮播卡。 由于瓦西里被卡片内容分散了注意力,因此在写信时,他可能会错误地用另一个字母代替一个字母,但众所周知,他总共只犯了k个错误。
瓦西里(Vasily)制作的唱片落入您的手中;您也知道k的值。 确定他的轮播中可以放几张卡片。
I / O格式和示例输入格式
第一行包含两个整数:n(1≤n≤500)-Basil写入的字符数,k(0≤k≤n)-Vasi所犯的最大错误数。
第二行包含n个拉丁字母的小写字母-Vasily编写的序列。
输出格式
打印单个整数正数-轮播中可能的最小卡数。
例子1
例子2
例子3
例子4
注意事项
在第一个示例中,k = 0,我们可以肯定地知道瓦西里没有记错,最小轮播可以由3张卡片组成-abc。
在第二个示例中,如果我们假定瓦西错误地将第三个字母a替换为c,则将获得最小的轮播长度。 则实际行是ababa,最小轮播包含2张卡片-ab。
在第三个示例中,众所周知Vasily可能会犯一个错误。 但是,假设他没有犯错误,轮播的大小是最小的。 最小轮播包括3张卡片-abb。 请注意,该轮播中的第二张和第三张相同。
在第四个示例中,我们可以说瓦西里在输入所有字母时被误认为,原始行实际上可以是任何行,例如ffffff。 然后,轮播可能包含一张卡片-f。
评分系统
只有通过了该任务的所有测试,您才能获得
50分 。
在测试系统中,测试1-4是条件示例。
解决方案
找出轮播的可能长度从1到n,并确定每个固定长度是否足够,就足够了。 显然,答案总是存在的,因为无论k的值如何,n的值都保证是可能的答案。 对于固定的轮播长度p,足以独立计算从0到(p-1)的所有i在位置i,i + p,i + 2p等处产生的最小错误数。如果将其视为真,则此错误数是最小的该符号是最常出现在这些位置的符号。 然后,错误数等于另一个字母所处的位置数。 如果对于某些p,错误总数不超过k,则值p是可能的答案。 由于对于每个p您都需要遍历字符串的所有字符一次,因此该算法的复杂度为O(n
2 )。
n, k = map(int, input().split()) s = input().strip() for p in range(1, n + 1): mistakes = 0 for i in range(0, p): counts = [0] * 26 for j in range(i, n, p): counts[ord(s[j]) - ord("a")] += 1 mistakes += sum(counts) - max(counts) if mistakes <= k: print(p) break
B1。 最佳推荐胶带
条件
对于用户而言,个人发布建议的下一部分的形成并非易事。 考虑基于候选人的选择从推荐库中选择的n种出版物。 出版物编号i的特征是相关性得分
si和一组k个二进制属性a
i1 ,
i i2 ,...,
ik 。 这些属性中的每一个都对应于出版物的某些属性,例如,用户是否订阅了该出版物的来源,是否在最近的24小时内创建了出版物等等。出版物可以一次具有多个这些属性,在这种情况下,相应的属性取值1,或者可能没有任何一个-然后其所有属性均为0。
为了使用户的供稿多样化,有必要在n个出版物的m个候选者之间进行选择,以使其中至少有具有第一属性的A
1个出版物,至少具有第二属性的A
2个出版物,...,具有以下属性的A
k个出版物:数字k 找到满足此要求的m个出版物的最大可能的总相关度得分,或确定不存在这样的一组出版物。
I / O格式和示例输入格式
第一行包含三个整数-n,m,k(1≤n≤50,1≤m≤min(n,9),1≤k≤5)。
接下来的n行显示出版物的特征。 第i个出版物的整数s(1≤s i≤10
9 )-对该出版物的相关性进行评估,然后以k个字符(每个字符为0或1)作为该出版物每个属性的值。
最后一行包含用空格分隔的k个整数-值A
1 ,...,A
k (0≤A i≤m),它们定义了m个出版物的最终集合的要求。
输出格式
如果没有m个满足条件的出版物,则打印数字0。否则,打印单个整数正数-可能的最大总相关分数。
例子1
例子2
注意事项
在第一个示例中,应从具有两个属性的四个出版物中选择两个,以便至少有一个具有第一个属性的出版物和一个具有第二个属性的出版物。 如果我们选择第二本和第三本出版物,则可以获得最大的相关性,尽管第四本出版物的任何选择也都适用于限制。
在第二个示例中,不可能选择两个发布,使其都具有第二个属性,因为只有第一个发布具有它。
评分系统
此任务的测试包括五个组。 仅当通过该组的所有测试和
以前的组的所有测试时,才会授予每个组的积分。 从条件通过测试对于从第二个开始获得组的分数是必要的。 总共可以得到
100分 。
在测试系统中,测试1-2是条件示例。
1.
(10分)测试3–10:k = 1,m≤3,s i≤1000,该条件无需测试
2.
(20分)测试11–20:k≤2,m≤3
3.
(20分)测试21–29:k≤2
4.
(20分)测试30–37:k≤3
5.
(30分)测试38-47:无其他限制
解决方案
有n个出版物,每个出版物都有速度和k个布尔标志,有必要选择m个卡片,以使相关性之和最大,并且满足“以下形式中的k个要求:“在所选择的m个出版物中必须具有≥i个带有第i个标志的卡片””,或确定这样的出版物不存在。
决定是10分 :如果只存在一个标记,则用这个标记具有最大相关性的A
1出版物就足够了(如果此类卡片的数量少于A
1 ,那么所需的集合就不存在),其余的(m-A
1 )应该由其余的选择。相关性最好的卡片。
解决方案是30分 :如果m不超过3,则可以通过详尽搜索所有可能的O(n
3 )张三元组找到答案,从总相关性方面选择满足限制的最佳选项。
决定是70分 (50分是相同的,只是更容易实现):如果标记不超过3个,则可以根据它们具有的标记集将所有发布分为8个不相交的组:000、001、010、011, 100、101、110、111。每组中的出版物应按相关性从高到低的顺序排序。 然后,对于O(m
4 ),我们可以从111、011、110和101组中挑选出多少种最佳出版物。从每种出版物中,我们选择0种到m种出版物,总共不超过m种。 此后,很明显需要从组100、010和001中收集多少出版物才能满足要求。 剩下的具有最高相关性的卡片仍然可以到达m。
完整的解决方案 :考虑动态编程功能dp [i] [a] ... [z]。 这是使用正好i个发布即可获得的最大总相关分数,因此恰好存在带有标志A,...,z带有标志Z的发布。然后,最初是dp [0] [0] ... [0] = 0,并且对于所有其他参数集,我们将值设置为-1,以便将来最大化该值。 接下来,我们将一次一张“进入游戏”卡,并使用每张卡来改善此功能的值:对于每个动态状态(i,a,b,...,z),请使用带有标记(a
j ,b
j ,...,z
j ),我们可以尝试转换为状态(i + 1,a + a
j ,b + b
j ,...,z + z
j ),并检查结果在此状态下是否有所改善。 重要说明:在过渡期间,我们对i≥m的状态不感兴趣,因此,此类动力学的总状态不超过m
k +1 ,并且所产生的渐近行为为O(nm
k +1 )。 当计算动力学状态时,答案是满足约束条件并给出最高总相关分数的状态。
从实现的角度来看,将动态编程的状态和每个出版物的标志以打包的形式存储在一个整数中以加速程序的工作(请参见代码),而不是在列表或元组中是有用的。 该解决方案使用更少的内存,并允许您有效地更新动态状态。
完整的解决方案代码:
def pack_state(num_items, counts): result = 0 for count in counts: result = (result << 8) + count return (result << 8) + num_items def get_num_items(state): return state & 255 def get_flags_counts(state, num_flags): flags_counts = [0] * num_flags state >>= 8 for i in range(num_flags): flags_counts[num_flags - i - 1] = state & 255 state >>= 8 return flags_counts n, m, k = map(int, input().split()) scores, attributes = [], [] for i in range(n): score, flags = input().split() scores.append(int(score)) attributes.append(list(map(int, flags))) limits = list(map(int, input().split())) dp = {0 : 0} for i in range(n): score = scores[i] state_delta = pack_state(1, attributes[i]) dp_temp = {} for state, value in dp.items(): if get_num_items(state) >= m: continue new_state = state + state_delta if value + score > dp.get(new_state, -1): dp_temp[new_state] = value + score dp.update(dp_temp) best_score = 0 for state, value in dp.items(): if get_num_items(state) != m: continue flags_counts = get_flags_counts(state, k) satisfied_bounds = True for i in range(k): if flags_counts[i] < limits[i]: satisfied_bounds = False break if not satisfied_bounds: continue if value > best_score: best_score = value print(best_score)
B2。 函数近似
条件
为了评估文档的相关程度,使用了各种机器学习方法-例如决策树。 第k个决策树在每个节点中都有一个决策规则,该规则根据一些属性的值将对象分为k类。 实际上,通常使用二进制决策树。 考虑优化问题的简化版本,必须在k元决策树的每个节点中解决该问题。
假设在点i = 1、2,...,n处定义一个离散函数f。 必须找到一个由不超过k个常数部分组成的分段常数函数g,以使值SSE =
(g(i)-f(i))
2是最小的。
I / O格式和示例输入格式
第一行包含两个整数n和k(1≤n≤300,1≤k≤min(n,10))。
第二行包含n个整数f(1),f(2),...,f(n)-点1、2,...,n(–10 6≤f(i)≤ 10
6 )。
输出格式
打印一个数字-SSE的最小可能值。 如果绝对或相对误差不超过10
–6,则认为答案正确。
例子1
例子2
例子3
注意事项
在第一个示例中,最佳函数g是常数g(i)= 2。
SSE =(2-1)
2 +(2-2)
2 +(2-3)
2 = 2。
在第二个示例中,有2个选项。 g(1)= 1和g(2)= g(3)= 2.5或g(1)= g(2)= 1.5或
g(3)=3。在任何情况下,SSE = 0.5。
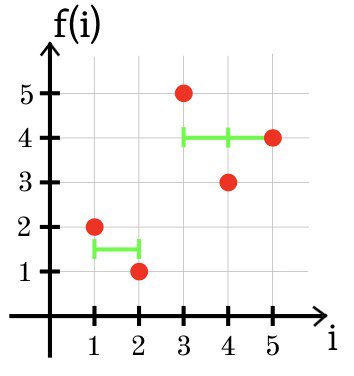
在第三个示例中,使用两个恒定部分的函数f的最佳逼近如下所示:g(1)= g(2)= 1.5和g(3)= g(4)= g(5)= 4。
SSE =(1.5 + 2)
2 +(1.5-1)
2 +(4-5)
2 +(4-3)
2 +(4-4)
2 = 2.5。
评分系统
此任务的测试包括五个组。 仅当通过该组的所有测试和
以前的组的所有测试时,才会授予每个组的积分。 从条件通过测试对于从第二个开始获得组的分数是必要的。 总共可以得到
100分 。
在测试系统中,测试1-3是条件示例。
1.
(10分)测试4–22:k = 1,无需从条件进行测试
2.
(20分)测试23–28:k≤2
3.
(20分)测试29–34:k≤3
4.
(20分)测试35–40:k≤4
5.
(30分)测试41-46:无其他限制
解决方案
如您所知,将一组值f
1 ,f
2 ,...,f
n的SSE值最小化的常数是此处列出的值的平均值。 此外,由于易于通过简单的计算进行验证,因此值SSE =
。
决定是10分 :我们仅将函数和SSE的所有值的平均值视为O(n)。
决定是30分 :我们整理出与两者恒定性的第一部分有关的最后一点,对于固定分区,我们计算SSE并选择最佳的。 此外,重要的是不要忘记只有一个恒定部分的情况下才可以拆开表壳。 难度-O(n
2 )。
决定是50分 :我们将划分的边界分类为O(n
2 )的恒定部分,对于分为3个部分的固定分区,我们计算SSE并选择最佳的一个。 难度-O(n
3 )。
决定是70分 :我们计算前缀上f
i的值的和与平方和,这将快速计算任何线段的平均值和SSE。 我们使用O(n
3 )前缀上的预先计算的值,将分区的边界分为O(n
3 )的4个恒定部分,从而计算SSE。 难度-O(n
3 )。
完整的解决方案 :考虑动态编程功能dp [s] [i]。 如果我们使用s段来近似前i个值,则这是最小的SSE值。 然后
dp [0] [0] = 0,对于所有其他参数集,我们将该值设置为无穷大,以便进一步将此值最小化。 我们将解决问题,逐渐增加s的值。 如果已经计算了所有较小s的动力学值,如何计算dp [s] [i]? 只需为t指定前一个(s-1)段所覆盖的第一点的数量,然后对t的所有值进行排序,并使用剩余的段来近似剩余的(i-t)点即可。 必须在i点为最终SSE选择最佳值t。 如果我们计算前缀上的f
i值的和和平方和,则将在O(1)中执行此近似,并且可以在O(n)中计算值dp [s] [i]。 最终答案是dp [k] [n]。 该算法的总复杂度为O(kn
2 )。
完整的解决方案代码:
n, k = map(int, input().split()) f = list(map(float, input().split())) prefix_sum = [0.0] * (n + 1) prefix_sum_sqr = [0.0] * (n + 1) for i in range(1, n + 1): prefix_sum[i] = prefix_sum[i - 1] + f[i - 1] prefix_sum_sqr[i] = prefix_sum_sqr[i - 1] + f[i - 1] ** 2 def get_best_sse(l, r): num = r - l + 1 s_sqr = (prefix_sum[r] - prefix_sum[l - 1]) ** 2 ss = prefix_sum_sqr[r] - prefix_sum_sqr[l - 1] return ss - s_sqr / num dp_curr = [1e100] * (n + 1) dp_prev = [1e100] * (n + 1) dp_prev[0] = 0.0 for num_segments in range(1, k + 1): dp_curr[num_segments] = 0.0 for num_covered in range(num_segments + 1, n + 1): dp_curr[num_covered] = 1e100 for num_covered_previously in range(num_segments - 1, num_covered): dp_curr[num_covered] = min(dp_curr[num_covered], dp_prev[num_covered_previously] + get_best_sse(num_covered_previously + 1, num_covered)) dp_curr, dp_prev = dp_prev, dp_curr print(dp_prev[n])
C.用户点击的预测
条件
推荐系统最重要的信号之一就是用户行为。 , .
..
2 : (train.csv) (test.csv). , . :
— sample_id — id ,
— item — id ,
— publisher — id ,
— user — id ,
topic_i, weight_i — id i- ( 0 100) (i = 0, 1, 2, 3, 4),
— target — (1 — , 0 — ). .
.
, item, publisher, user, topic .
csv-, : sample_id target, sample_id — id , target — . test.csv. sample_id ( , test.csv). target 0 1.
logloss.
150 . logloss :
logloss . 2 , logloss 4 .
/输入格式
片段train.csv:片段test.csv:输出格式
可能的解决方案文件的片段:注意事项
:
yadi.sk/d/pVna8ejcnQZK_A . , .
logloss :
EPS = 1e-4
def logloss(y_true, y_pred):
if abs (y_pred - 1) < EPS:
y_pred = 1 - EPS
if abs (y_pred) < EPS:
y_pred = EPS
return -y_true ∗ log(y_pred) - (1 - y_true) ∗ log(1 - y_pred)logloss logloss .
logloss :
def score(logloss):
if logloss > 0.5:
return 0.0
return min(150, (200 ∗ (0.5 - logloss)) ∗∗ 2) , . . , (, , , ) , — , - , .
, 100 ( 150).
— CatBoost . CatBoost ( ), . , . , -:
( ), , , , - ( ).
. , - , : FM (Factorization Machines) FFM (Field-aware Factorization Machines).
,
ML- .