卷积层：根据Shmuel Vinograd的方法进行快速卷积

引言

本文是描述基础算法的一系列文章的续篇。
Synet是用于在CPU上启动预训练的神经网络的框架。

在上一篇文章中，我描述了基于矩阵乘法的方法。 这些方法用最少的精力在许多情况下可以达到理论最大值的80％以上。 看来，我们可以在哪里进一步改进它？ 事实证明你可以！ 有一些数学方法可以减少卷积所需的运算数量。 在本文中，我们将熟悉其中一种方法，即通过Vinograd方法的卷积算法。


Shmuel Winograd 1936.01.04-2019.03.25-以色列和美国杰出的计算机科学家，快速矩阵乘法，卷积和傅立叶变换算法的创建者。

一点数学

尽管在机器学习中，最常使用具有方形核的卷积，但是为了简化表示，我们将首先考虑一维情况。 假设我们有一个尺寸为1维的输入一维图像 $$$1 \次4$ ：

$$

$$d = \开始{bmatrix} d_0＆d_1＆d_2＆d_3 \结束{bmatrix} ^ T，$$

和过滤器尺寸 $$$1 \次3$ ：

$$

$$g = \开始{bmatrix} g_0＆g_1＆g_2 \结束{bmatrix} ^ T，$$

那么卷积的结果将是：

$$

$$F（2,3）= \开始{bmatrix} d_0 g_0 + d_1 g_1 + d_2 g_2 \\ d_1 g_0 + d_2 g_1 + d_3 g_2 \结束{bmatrix}。$$

这些表达式可以方便地以矩阵形式重写：

$$

$$F（2,3）= \开始{bmatrix} d_0＆d_1＆d_2 \\ d_1＆d_2＆d_3 \结束{bmatrix} \开始{bmatrix} g_0 \\ g_1 \\ g_2 \结束{bmatrix} = \开始{bmatrix} d_0 g_0 + d_1 g_1 + d_2 g_2 \\ d_1 g_0 + d_2 g_1 + d_3 g_2 \结束{bmatrix} = \开始{bmatrix} m_1 + m_2 + m_3 \\ m_2-m_3-m_4 \结束{bmatrix}， （1）美$$

使用符号的地方：

$$

$$m_1 =（d_0-d_2）g_0，\\ m_2 =（d_1 + d_2）\ frac {g_0 + g_1 + g_2} {2}，\\ m_3 =（d_2-d_1）\ frac {g_0-g_1 + g_2} {2}，\\ m_4 =（d_1-d_3）g_2$$

乍一看，最后一次更换似乎毫无意义-显然还有更多的操作。 但是表达 $$$\ frac {g_0 + g_1 + g_2} {2}$ 和 $$$\ frac {g_0-g_1 + g_2} {2}$ 只需要计算一次。 考虑到这一点，我们只需要执行4次乘法运算，而在原始公式中则需要完成6次乘法运算。
我们重写表达式（1）：

$$

$$F（2,3）= A ^ T [（G g）\ odot（B ^ T d）]，（2）$$

在哪里 $$$\ odot$ 表示逐元素相乘，并且还使用以下表示法：

$$

$$B ^ T = \开始{bmatrix} 1＆0＆-1＆0 \\ 0＆1＆1＆0 \\ 0＆-1＆1＆0 \\ 0＆1＆0＆-1 \ end { bmatrix}，（3）\\ G = \开始{bmatrix} 1＆0＆0 \\ \ frac {1} {2}＆\ frac {1} {2}＆\ frac {1} {2} \\ \ frac {1} {2}＆-\ frac {1} {2}＆\ frac {1} {2} \\ 0＆0＆1 \ end {bmatrix}，（4）\\ A ^ T = \开始{bmatrix} 1＆1＆1＆0 \\ 0＆1＆-1＆-1 \结束{bmatrix}。 （5）$$

表达式（2）可以推广到二维情况：

$$

$$F（2 \ times2,3 \ times3）= A ^ T \ bigg [[G g G ^ T] \ odot [B ^ T d B] \ bigg]A。（6）$$

所需的乘法运算数量 $$$F（2 \ times2,3 \ times3）$ 从...缩水 $$$2 \ times2 \ times3 \ times3 = 36$ 之前 $$$4 \ times4 = 16$ 。 这样我们得到了 $$$\ frac {36} {16} = $ 2.2$ 次。 如果您进行可视化，那么实际上，我们将立即为一个大小块计算它，而不是分别计算图像中每个点的卷积 $$$2 \ times2$ ：

无论如何，为了与窗口卷积 $$$r \乘以s$ 和块大小 $$$m \次n$ 所需的乘法数将是

$$

$$count =（m + r-1）\次（n + s-1），（7）$$

增益由以下公式描述：

$$

$$k = \ frac {m \次数n \次数r \次数s} {（m + r-1）\次数（n + s-1）}。 （8）$$

在极限范围内 $$$m$ 和 $$$n$ 对于任何卷积，只需要1个乘法乘以一点就足够了！ 不幸的是，块大小的增加导致输入开销的迅速增加 $$$B ^ T d B$ 和周末 $$$A ^ T [...] A$ 图片，因此在实践中通常不使用大于 $$$4 \次4$ 。

实施实例

对于Vinograd算法的实际实现，我想考虑最简单的情况-与内核的卷积 $$$3 \次3$ 对于块 $$$2 \ times2$ 。 为了进一步简化表示，我们还将假设输入图像没有填充，输入和输出图像的大小是2的倍数。

基于矩阵乘法的卷积实现将如下所示：

float relu(float value) { return value > 0 ? return value : 0; } void gemm_nn(int M, int N, int K, float alpha, const float * A, int lda, float beta, const float * B, int ldb, float * C, int ldc) { for (int i = 0; i < M; ++i) for (int j = 0; j < N; ++j) { C[i*ldc + j] = beta; for (int k = 0; k < K; ++k) C[i*ldc + j] += alpha * A[i*lda + k] * B[k*ldb + j]; } } void im2col(const float * src, int srcC, int srcH, int srcW, int kernelY, int kernelX, float * buf) { int dstH = srcH - kernelY + 1; int dstW = srcW - kernelX + 1; for (int sc = 0; sc < srcC; ++sc) for (int ky = 0; ky < kernelY; ++ky) for (int kx = 0; kx < kernelX; ++kx) for (int dy = 0; dy < dstH; ++dy) for (int dx = 0; dx < dstW; ++dx) *buf++ = src[((b * srcC + sc)*srcH + dy + ky)*srcW + dx + kx]; } void convolution(const float * src, int batch, int srcC, int srcH, int srcW, int kernelY, int kernelX, int dilationY, int dilationX, int strideY, int strideX, int padY, int padX, int padH, int padW, int group, const float * weight, const float * bias, float * dst, int dstC, float * buf) { int dstH = srcH - kernelY + 1; int dstW = srcW - kernelX + 1; int M = dstC; int N = dstH * dstW; int K = srcC * kernelY * kernelX; for (int b = 0; b < batch; ++b) { im2col(src, srcC, srcH, srcW, kernelY, kernelX, buf); gemm_nn(M, N, K, 1, weight, K, 0, buf, N, dst, N)); for (int i = 0; i < M; ++i) for (int j = 0; j < N; ++j) dst[i*N+ j] = relu(dst[i*N + j] + bias[i]); src += srcC*srcH*srcW; dst += dstC*dstH*dstW; } } 

那些想详细了解这里发生的事情的人应该转向我以前的文章 。 当前的实现是从上一个实现中获得的，前提是：

 strideY = strideX = dilationY = dilationX = group = 1, padY = padX = padH = padW = 0. 

改进的卷积算法

我在这里再次给出公式（6）：

$$

$$F（2 \ times2,3 \ times3）= A ^ T \ bigg [[G g G ^ T] \ odot [B ^ T d B] \ bigg] A.$$

如果从输出图像尺寸切换 $$$2 \ times2$ 到任意大小的图像，那么我们将不得不将其分成大小块 $$$2 \ times2$ 。 对于每个这样的块，将形成输入图像 $$$（2 + 3-1）\次（2 + 3-1）= $ 1$ 16个转换后包含的值 $$$B ^ T d B$ 输入图像缩小一半。 然后，将这16个矩阵中的每个矩阵与变换后的权重的相应矩阵相乘 $$$G g G ^ T$ 。 将16个结果矩阵转换为输出图像 $$$A ^ T \ bigg [... \ bigg] A$ 。 下图显示了此过程：



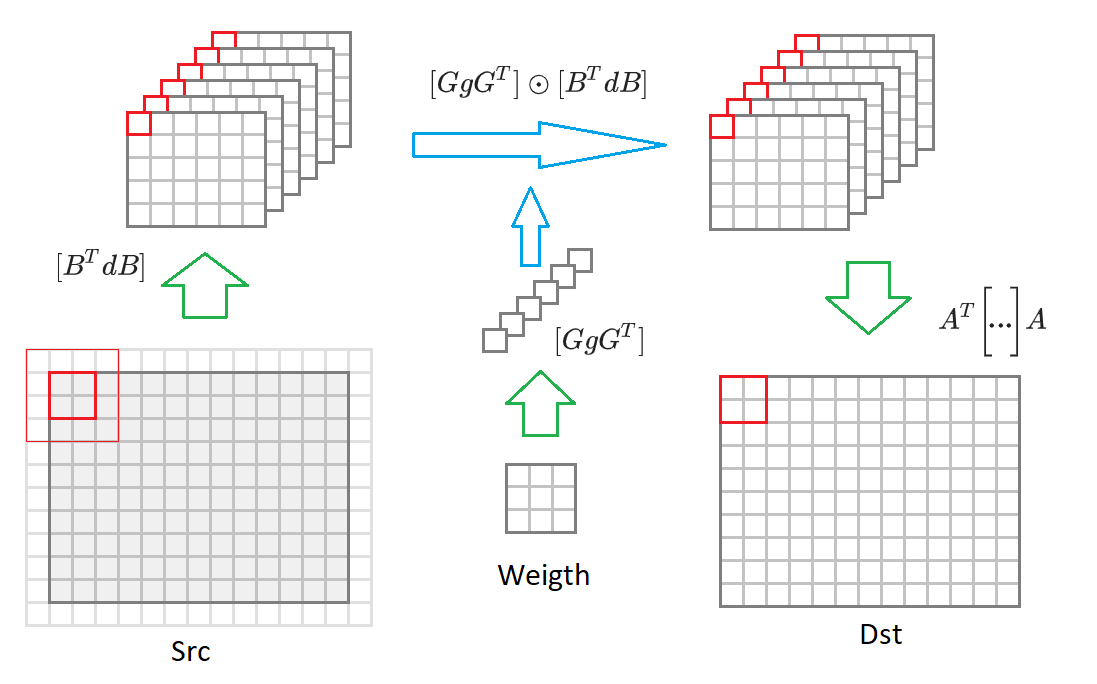
鉴于这些评论，卷积算法采用以下形式：

 void convolution(const float * src, int batch, int srcC, int srcH, int srcW, int kernelY, int kernelX, int dilationY, int dilationX, int strideY, int strideX, int padY, int padX, int padH, int padW, int group, const float * weight, const float * bias, float * dst, int dstC, float * buf) { const int block = 2, kernel = 3; int count = (block + kernel - 1)*(block + kernel - 1); // 16 int dstH = srcH - kernelY + 1; int dstW = srcW - kernelX + 1; int tileH = dstH / block; int tileW = dstW / block; int sizeW = srcC * dstC; int sizeS = srcC * tileH * tileW; int sizeD = dstC * tileH * tileW; int M = dstC; int N = tileH * tileW; int K = srcC; float * bufW = buf; float * bufS = bufW + sizeW*count; float * bufD = bufS + sizeS*count; set_filter(weight, sizeW, bufW); for (int b = 0; b < batch; ++b) { set_input(src, srcC, srcH, srcW, bufS, sizeS); for (int i = 0; i < count; ++i) gemm_nn(M, N, K, 1, bufW + i * sizeW, K, bufS + i * sizeS, N, 0, bufD + i * sizeD, N)); set_output(bufD, sizeD, dst, dstC, dstH, dstW); for (int i = 0; i < M; ++i) for (int j = 0; j < N; ++j) dst[i*N+ j] = relu(dst[i*N + j] + bias[i]); src += srcC*srcH*srcW; dst += dstC*dstH*dstW; } } 

在不考虑输入和输出图像转换的情况下所需的操作数： 〜srcC * dstC * dstH * dstW * count 。 接下来，我们描述用于转换权重，输入和输出图像的算法。

转换卷积尺度

从表达式（6）可以看出，应对卷积权重执行以下转换： $$$G g G ^ T$ 矩阵在哪里 $$$G$ 在表达式（4）中定义。 该转换的代码如下所示：

 void set_filter(const float * src, int size, float * dst) { for (int i = 0; i < size; i += 1, src += 9, dst += 1) { dst[0 * size] = src[0]; dst[1 * size] = (src[0] + src[2] + src[1])/2; dst[2 * size] = (src[0] + src[2] - src[1])/2; dst[3 * size] = src[2]; dst[4 * size] = (src[0] + src[6] + src[3])/2; dst[5 * size] = ((src[0] + src[6] + src[3]) + (src[2] + src[8] + src[5]) + (src[1] + src[7] + src[4]))/4; dst[6 * size] = ((src[0] + src[6] + src[3]) + (src[2] + src[8] + src[5]) - (src[1] + src[7] + src[4]))/4; dst[7 * size] = (src[2] + src[8] + src[5])/2; dst[8 * size] = (src[0] + src[6] - src[3])/2; dst[9 * size] = ((src[0] + src[6] - src[3]) + (src[2] + src[8] - src[5]) + (src[1] + src[7] - src[4]))/4; dst[10 * size] = ((src[0] + src[6] - src[3]) + (src[2] + src[8] - src[5]) - (src[1] + src[7] - src[4]))/4; dst[11 * size] = (src[2] + src[8] - src[5])/2; dst[12 * size] = src[6]; dst[13 * size] = (src[6] + src[8] + src[7])/2; dst[14 * size] = (src[6] + src[8] - src[7])/2; dst[15 * size] = src[8]; } } 

幸运的是，此转换只需要执行1次。 因此，它不会影响最终性能。

输入图像转换

从表达式（6）可以看出，应该对输入图像执行以下变换： $$$B ^ T d B$ 矩阵在哪里 $$$B ^ T$ 在表达式（3）中定义。 该转换的代码如下所示：

 void set_input(const float * src, int srcC, int srcH, int srcW, float * dst, int size) { int dstH = srcH - 2; int dstW = srcW - 2; for (int c = 0; c < srcC; ++c) { for (int row = 0; row < dstH; row += 2) { for (int col = 0; col < dstW; col += 2) { float tmp[16]; for (int r = 0; r < 4; ++r) for (int c = c; c < 4; ++c) tmp[r * 4 + c] = src[(row + r) * srcW + col + c]; dst[0 * size] = (tmp[0] - tmp[8]) - (tmp[2] - tmp[10]); dst[1 * size] = (tmp[1] - tmp[9]) + (tmp[2] - tmp[10]); dst[2 * size] = (tmp[2] - tmp[10]) - (tmp[1] - tmp[9]); dst[3 * size] = (tmp[1] - tmp[9]) - (tmp[3] - tmp[11]); dst[4 * size] = (tmp[4] + tmp[8]) - (tmp[6] + tmp[10]); dst[5 * size] = (tmp[5] + tmp[9]) + (tmp[6] + tmp[10]); dst[6 * size] = (tmp[6] + tmp[10]) - (tmp[5] + tmp[9]); dst[7 * size] = (tmp[5] + tmp[9]) - (tmp[7] + tmp[11]); dst[8 * size] = (tmp[8] - tmp[4]) - (tmp[10] - tmp[6]); dst[9 * size] = (tmp[9] - tmp[5]) + (tmp[10] - tmp[6]); dst[10 * size] = (tmp[10] - tmp[6]) - (tmp[9] - tmp[5]); dst[11 * size] = (tmp[9] - tmp[5]) - (tmp[11] - tmp[7]); dst[12 * size] = (tmp[4] - tmp[12]) - (tmp[6] - tmp[14]); dst[13 * size] = (tmp[5] - tmp[13]) + (tmp[6] - tmp[14]); dst[14 * size] = (tmp[6] - tmp[14]) - (tmp[5] - tmp[13]); dst[15 * size] = (tmp[5] - tmp[13]) - (tmp[7] - tmp[15]); dst++; } } src += srcW * srcH; } } 

此转换所需的操作数为： 〜srcH * srcW * srcC * count 。

输出图像转换

从表达式（6）可以看出，应该对输出图像执行以下转换： $$$A ^ T [...] A$ 矩阵在哪里 $$$B ^ T$ 在表达式（5）中定义。 该转换的代码如下所示：

 void set_output(const float * src, int size, float * dst, int dstC, int dstH, int dstW) { for (int c = 0; c < dstC; ++c) { for (int row = 0; row < dstH; row += 2) { for (int col = 0; col < dstW; col += 2) { float tmp[8]; tmp[0] = src[0 * size] + src[1 * size] + src[2 * size]; tmp[1] = src[1 * size] - src[2 * size] - src[3 * size]; tmp[2] = src[4 * size] + src[5 * size] + src[6 * size]; tmp[3] = src[5 * size] - src[6 * size] - src[7 * size]; tmp[4] = src[8 * size] + src[9 * size] + src[10 * size]; tmp[5] = src[9 * size] - src[10 * size] - src[11 * size]; tmp[6] = src[12 * size] + src[13 * size] + src[14 * size]; tmp[7] = src[13 * size] - src[14 * size] - src[15 * size]; dst[col + 0] = tmp[0] + tmp[2] + tmp[4]; dst[col + 1] = tmp[1] + tmp[3] + tmp[5]; dst[dstW + col + 0] = tmp[2] - tmp[4] - tmp[6]; dst[dstW + col + 1] = tmp[3] - tmp[5] - tmp[7]; src++; } dst += 2*dstW; } } } 

此转换所需的操作数为： 〜dstH * dstW * dstC * count 。

实际实施的特点

在上面的示例中，我们描述了针对块大小的Vinohrad算法 $$$2 \ times2$ 。 实际上，最常用的算法是更高级的版本： $$$F（4 \ times4,3 \ times3）$ 。 在这种情况下，块大小将为 $$$4 \次4$ ，并且变换后的矩阵数为36。根据公式（8），计算增益将达到4 。 该算法的一般方案是相同的，只是变换算法的矩阵不同。

Github上有一个小项目 ，您可以使用任意卷积核大小和块大小的系数来计算这些矩阵。

我们为NCHW图像格式提出了 Vinograd算法的一种变体，但是对于NHWC格式可以用类似的方法来实现（我在上一篇文章中谈到了这些图像格式的细节。

尽管存在其他转换，但Vinograd算法（当然具有其出色的应用程序）的主要计算负荷仍然在于矩阵乘法。 幸运的是，这是一个标准操作，已在许多库中有效地实现。

在此处可以找到针对Vinohrad算法针对不同平台优化的转换函数。

Grape算法的优缺点

首先，当然是优点：

• 该算法允许多次（通常是2-3次）来加快卷积的计算速度。 因此，有可能比“理论”极限更快地计算卷积。
• 该算法的实现依赖于标准矩阵乘法算法。
• 它可以为各种输入图像格式实现： NCHW ， NHWC 。
• 用于存储中间值的缓冲区大小小于矩阵乘法算法所需的大小。

好，没有缺点的地方：

• 该算法需要针对每个卷积内核大小以及每个块大小分别实现转换函数。 也许这是几乎仅在与内核卷积一起实现的所有地方的主要原因之一。 $$$3 \次3$ 。
• 随着块大小的增长，实现转换功能的复杂性迅速增长。 因此，实际上没有块大小大于 $$$4 \次4$ 。
• 该算法对卷积参数strideY = strideY = dilationY = dilationX = group = 1施加了严格的限制。 尽管从理论上讲，可以在违反这些限制时实施该算法，但实际上由于效率低而适用性不强。
• 如果图像中输入或输出通道的数量很少，则算法的效率会降低（这是由于转换输入和输出图像的成本所致）。
• 对于小尺寸的输入图像（从输入图像得到的矩阵太小，并且标准矩阵乘法算法对其无效），该算法的效率会降低。

结论

与基于简单矩阵乘法的方法相比，基于Vinograd算法的卷积计算方法可以显着提高计算效率。 不幸的是，它不是通用的，很难实施。 对于许多特殊情况，有更快的方法，我想将其描述推迟到本系列的下一篇文章中。 等待读者的反馈和意见。 希望你有兴趣！

PS这种方法和其他方法是由我在卷积框架中作为Simd库的一部分实现的。
该框架是Synet的基础， Synet是用于在CPU上运行预训练的神经网络的框架。