想象一下,您被一堵无限高的墙包围着,但是对于墙背后的东西一无所知。 现在,假设这堵墙的拟人化是以下等式:
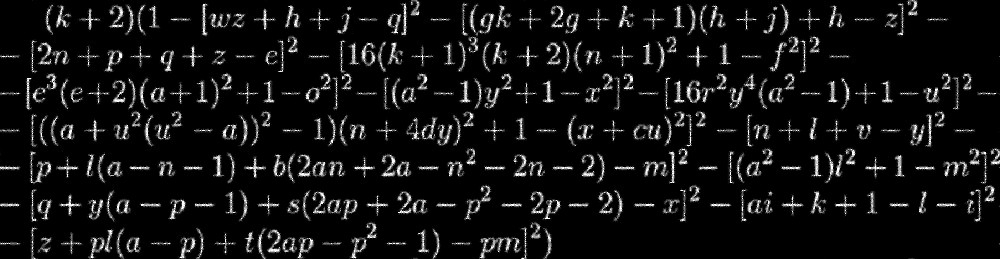
如果我们用一个黑洞进行类比,那么这个隐喻将更容易理解:我们不知道其事件的范围是什么,要弄清楚我们需要想出一种方法来达到目标。 在数学世界中也存在类似的情况。 这个方程式是素数的实数“公式”,但是要使用它,我们需要弄清楚如何寻找合适的
{a,b,c,d,e,f,g,h,i,j,k,l,m, n,o,p,q,w,v,x,y,z} 。
黑洞和该等式是真实的抽象事物的最终状态。 而且,如果对第一个有足够的猜测和想法,那么对第二个则几乎一无所知。 但是,如果它确实是一个“数学上的”黑洞怎么办? 您是否很好奇如果我们跌破地平线会发生什么?
墙由什么组成?
数字-它们不在现实世界中。 有七个骰子,七个原子,七个致命罪,但七个本身不存在-这是一种抽象。 是的,我们可以说数字只是很多抽象对象,但是,这是一个整个世界。 和现实世界一样,世界上有法律。 这种想法似乎很奇怪。 尽管如此,作为数论的数学分支的存在表明,这种“奇数”对我们来说非常重要。
最令人兴奋的是,在这些虚构对象中,有一些特殊的对象-质数。 它们就像确定性混乱一样-同时取决于可考虑的范围,可预测和不可预测。 例如,在它们旁边,我们可以注意到在任意数字n前面的数字不会超过:
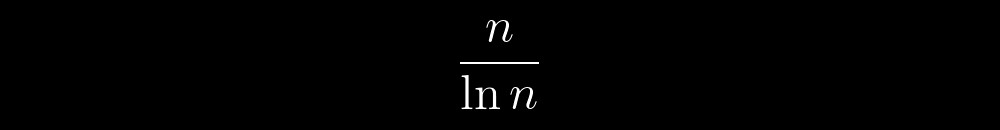
改变规模后,我们开始注意到许多有关其行为的内部规则的提示。 逐渐地,这些提示变得太多了。 越来越多的问题是“它们是从哪里来的?”,“如果有某种获取质数的算法该怎么办?”,“如果可以使用相同的算法获得每个质数怎么办?”
墙如何出现
如果由于某种算法的操作而获得了某个数字序列,那么即使该序列的数字集可以无限大,它也被认为是可枚举的。 枚举集具有一项非凡的特性-Diophantine。 这意味着任何这样的集合都可以用Diophantine方程表示-具有整数正系数和幂的多项式。
以下陈述似乎是完全不可行的,但基于此定义,我们可以辩称,所有安全密钥和哈希函数(甚至是比特币)的值都可以通过Diophantine方程表示。 即 以整数形式求解的方程。 是的,从理论上讲,一个人可以学习任何秘密,成为一个有钱人和有权力的人。 但是,为了成为这样的人,必须首先推导这些方程式,然后求解。
计算机可以处理部分地或全部地用丢丢丁方程表示集合的任务。 但是这里出现了另一个问题-Diophantine方程不是以一般形式求解的,即 没有解决这些问题的单一算法。 这似乎不是一个大问题,因为我们知道某些方程式可以区分为不同的形式,对于它们的解决方案,已经找到了有效的方法。
但是,即使存在这些方法,我们也不可避免地会遇到与计算精度或迭代速度有关的计算难题。
素数是怎么发生的? 创建表示可数集的方程式的过程完全依赖数学的基础-算术和逻辑。 并且,如果我们对某个集合的对象的属性有足够的了解,则可以基于此知识对可以获取对象的算法进行假设。 而且,事实证明,有关质数性质的知识已足够为此目的而积累。 已经获得了方程,现在所有与质数有关的问题都简化为方程。
但是我们无法解决。
壁厚和强度
实际上,我们面临挑战。 我们事先知道了不可避免的失败。 撤退也许是最明智的决定。 但是我们是否需要这些失败才能超越自己? 让我们尝试一点解决。
再次看一下等式:
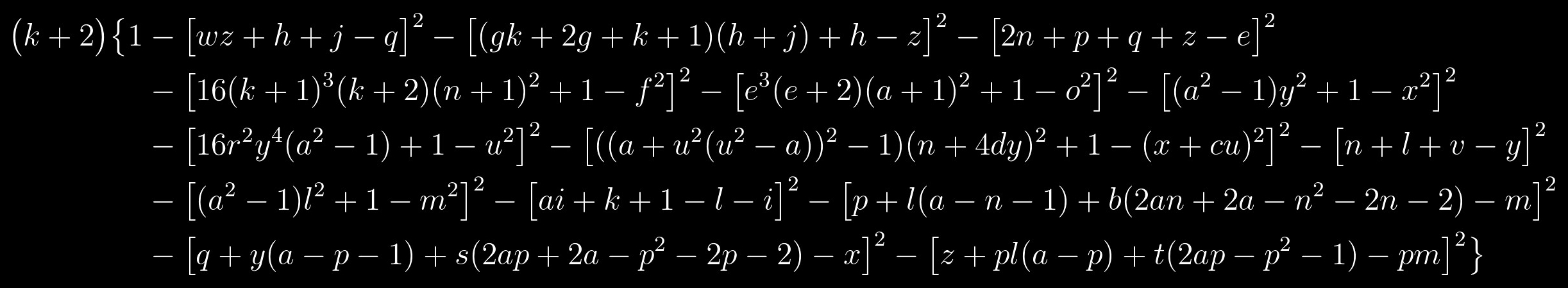
这是一个多项式,其正值组与素数组重合。 它由两个因子组成:左因子只有在用大括号表示的右因子等于1时才是质数,而这又仅在给定因子中每个用方括号表示的项等于0时才有可能。 。 事实证明,求解此方程的问题简化为以下方程组的求解:
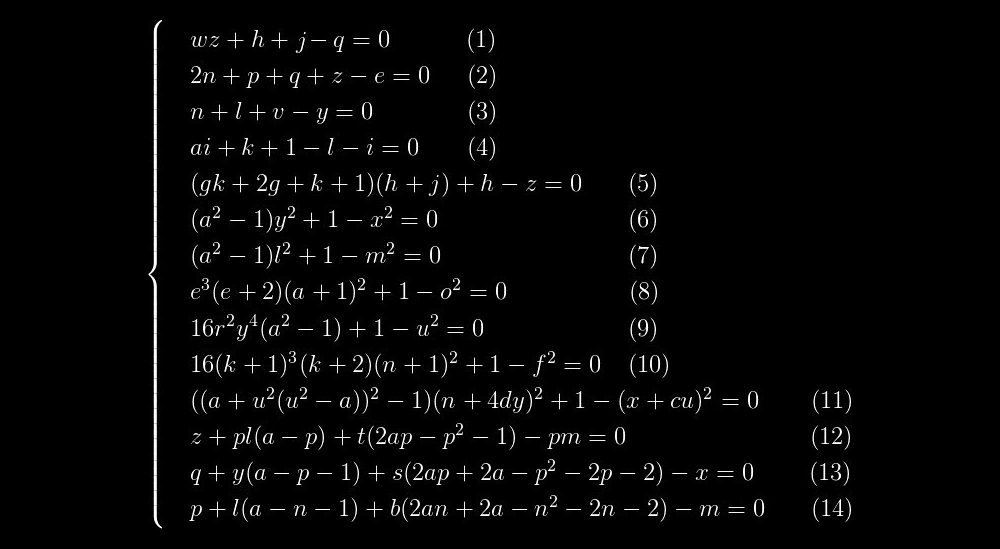
如果我们求解此方程组并将
k的找到的值加2,则得到一个质数。 但是我们可以走另一条路。 取一些质数,从中减去2,从而获得
k的值,然后将该值替换为系统,并尝试查找相对于其的其余变量的值。 我们将采用这种方式-尝试为此多项式找到至少一个解决方案。
所有变量都有两个严格的限制;它们必须是整数,并且不能为负数。 如果我们使
k = 0 ,那么我们可以获得的第一个质数是2。这将是我们的起点。 将这个值代入方程式系统后,它将采用以下形式:
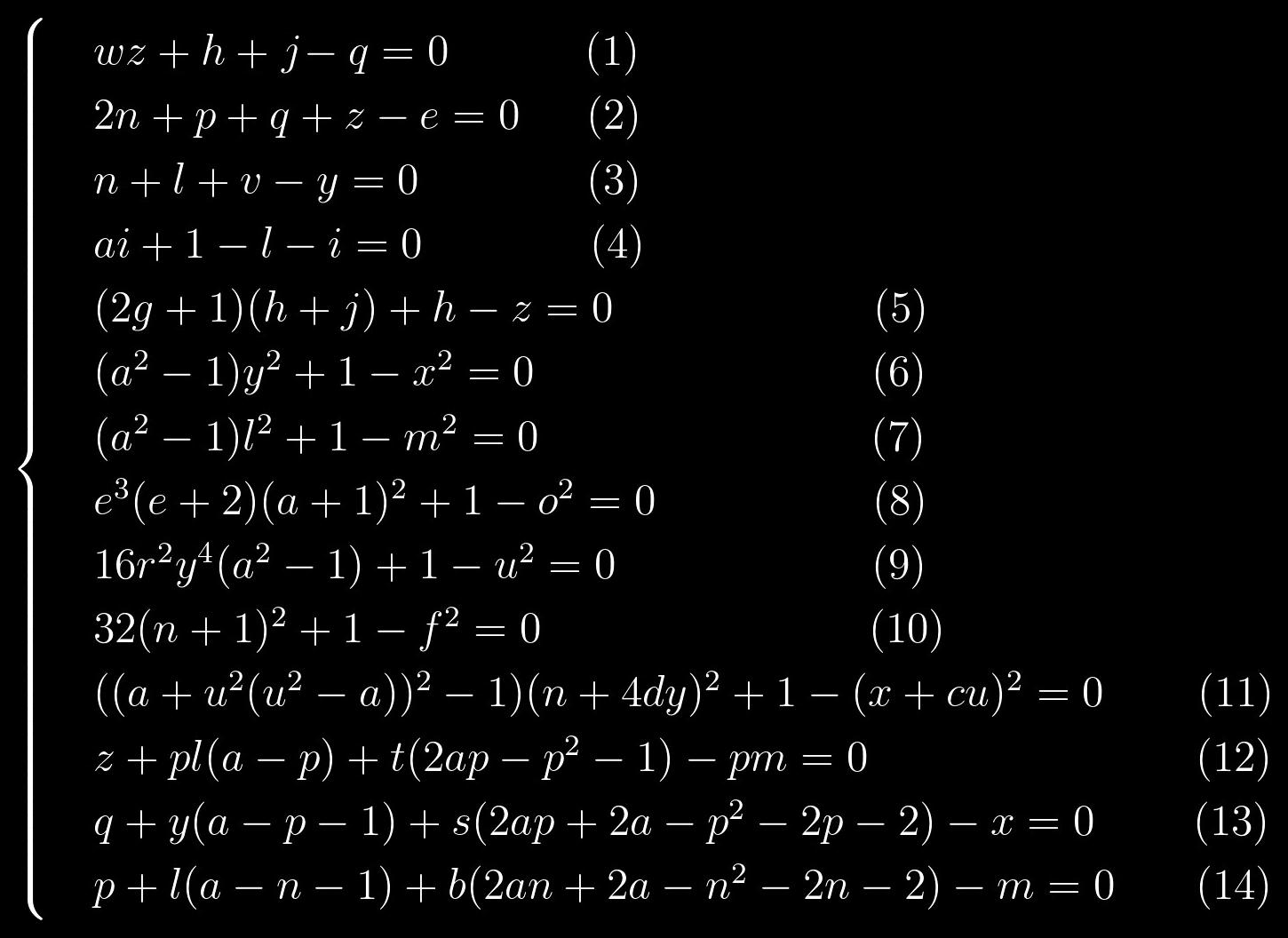
等式(1)-(5)是线性方程,即。 所有变量的度均为1。公式(6)-(11)具有非常相似的结构。 最后,方程式(12)-(14)在另一个单独的组中也很突出,方程式(13)和(14)彼此相似,就像两滴水一样。
我们可以摆脱变量,或者降低程度,但是我们之前已经做过。 变量数量的减少会导致其他变量的程度大大增加,而变量程度的减少只有通过增加其数量才有可能。 因此,让我们尝试以这种形式解决该系统。
公式(6)-(11)是Pell公式的修改:
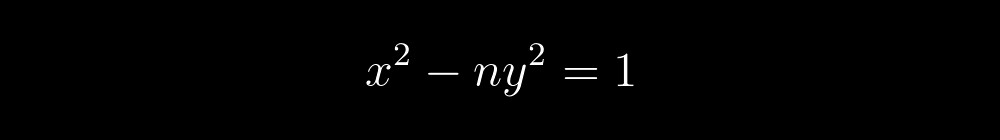
实际上,如果您这样重写它们:
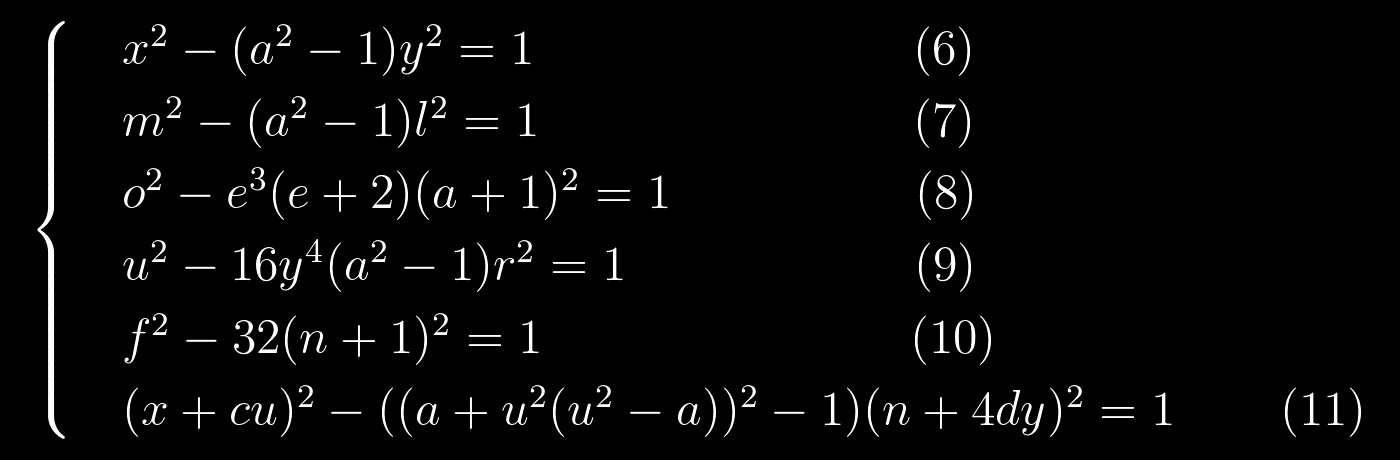
那么相似性就显而易见了。 这非常令人鼓舞,因为我们能够很好地解决Pell方程。 我们可以尝试这样解决该系统:首先,我们解决一个方程,将其解替换为另一个方程,然后我们也求解,依此类推,直到最后。 听起来很简单,但是画一个排列图之类的东西至少可以粗略地知道以什么顺序求解方程式,这并没有什么坏处:
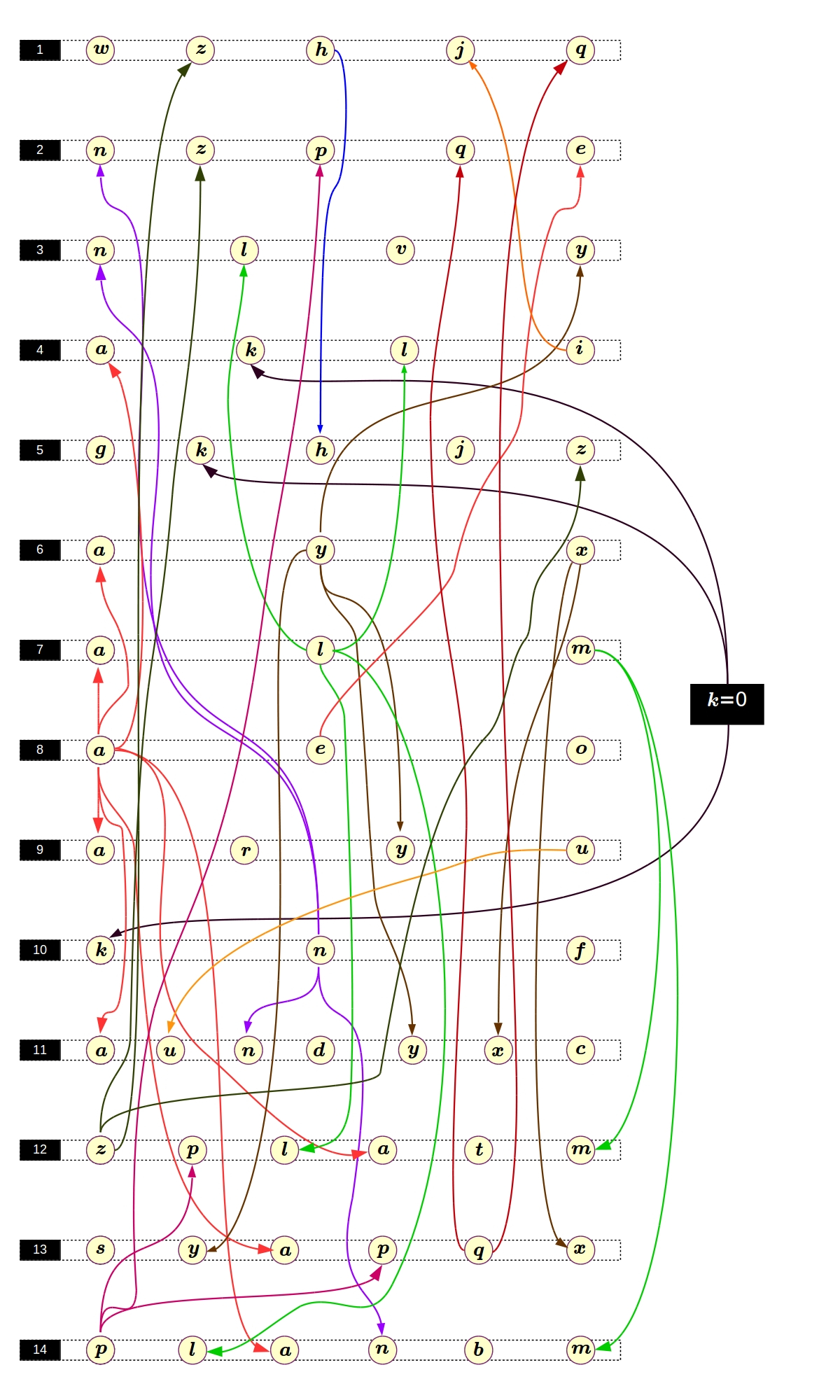
似乎一切都很简单。
踢在墙上
我们从佩尔方程开始。 为了解决它们,我们将编写一个小脚本:
from decimal import * getcontext().prec = 50 def peq_dec(N): n = Decimal(N).sqrt() a = int(n) x = n - a p0, q0 = 1, 0 p1, q1 = int(a), 1 while True: a = int(1/x) x = 1/x - a p_i = a*p1 + p0 q_i = a*q1 + q0 if p_i**2 - N*q_i**2 == 1: return p_i, q_i break p0, q0 = p1, q1 p1, q1 = p_i, q_i
多亏了他,我们才能立即找到方程(10)的解
n = 2 ,
f = 17 。 但是,在继续之前,我们需要了解有关Pell方程的知识。
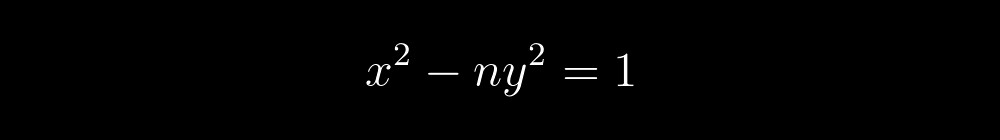
首先,
n不能是一个完整的正方形。 此外,任何Pell方程都有无数个解,其中总是有一个平凡的解:
x = 1和
y = 0 。 根据以下重复公式,可以在先前决定的基础上获得每个后续决定:
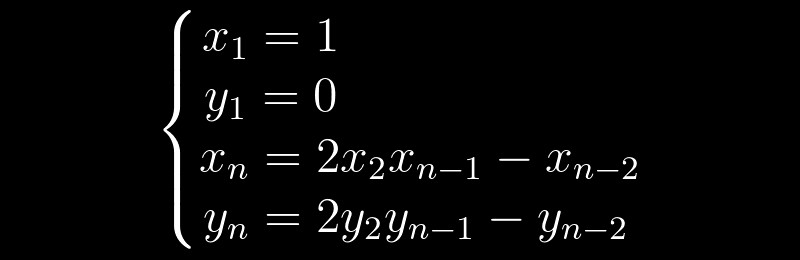
事实证明,对于我们而言,找到最小的平凡解决方案就足够了,我们可以使用简单的算法获得所有其余解决方案。 例如,对于
n = 2,我们可以轻松找到这样的解,它是
x = 3和
y = 2 ,那么后续的解将如下所示:
17, 12 99, 70 577, 408 3363, 2378 19601, 13860 114243, 80782 665857, 470832 3880899, 2744210 22619537, 15994428 131836323, 93222358 768398401, 543339720 4478554083, 3166815962 26102926097, 18457556052 152139002499, 107578520350 886731088897, 627013566048
值得继续做进一步的决定吗? 当然这是值得的,但是...我们可以尝试预测未来。
现在就让我们想象一下,我们正在解决以下形式的三个Pell方程的方程组:
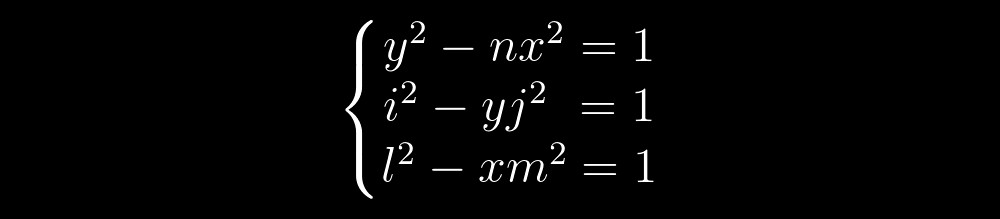
任何佩尔方程的解决方案都是具有整数坐标的双曲线点。 然后,我们可以想象这样的前两个方程的解决方案:
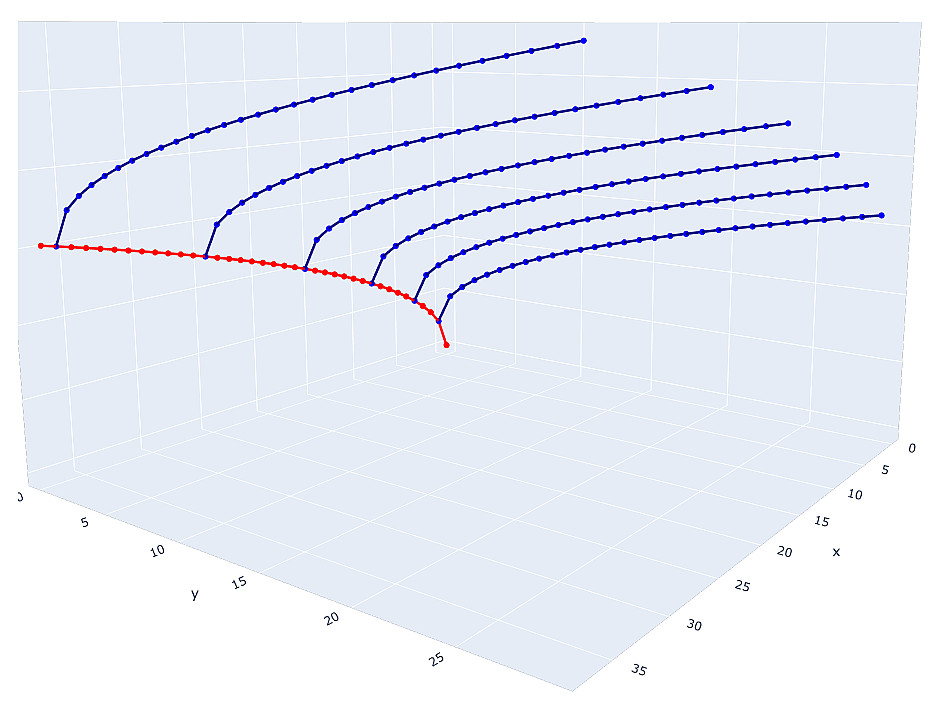
第一个方程的解是红色双曲线的整数点,但是每个点的
y坐标出现在第二个方程中,并且可以生成任何蓝色双曲线,其蓝色的双点将成为第二个方程的解。
即使是该示意图也足以了解我们正在处理大量潜在的候选者来解决该系统。 为什么要应聘? 因为双曲线的某些整数点将必定是实心平方,即 不适当的解决方案。 而且,如果您想对系统中的每个变量强加任何其他条件,那么寻找解决方案的候选人将变得极为困难。 到目前为止,我们仅讨论由三个方程组成的系统。
但是,让我们回到素数的“公式”。 我们面前会发生什么?
迟早,我们将发现Pell方程中的参数
n会变得灾难性地大。 连续分数的方法将变得毫无用处。 我们一定会尝试其他方法,例如通过筛选枚举值,以某种方式概括整个过程,并得出诸如二次筛或数字场筛之类的算法。 最后,我们将重点介绍“ chakraval”方法,尽管它也会遇到一些困难。
在某个时刻,我们将对系统中每个方程的解有一定的信心。 但不是整个系统。 我们将尝试应用一些启发式优化方法,例如退火算法或蚂蚁算法。 但是在这里我们会失败。 为了至少以某种方式理解这些失败的原因,我们将不得不深入研究代数几何和拓扑。 逐渐地,我们将对“可结晶物质”有所了解。 我们可以远程想象释放蚂蚁的超曲面的结构。
基于这些想法,我们将尝试改进算法。 为此,我们将从许多数学分支中取得最好的成绩。 逐渐地,算法的机会将减少,但是您仍然无法摆脱它。 接下来会发生什么? 我们突然发现,在某些地方,许多适合做出真实决定的候选人都充满了矛盾。 每一个这样的密度都会给人以希望,在其中心的某个地方隐藏了答案。 这样的密度对蚂蚁来说就像是倒置的超漏斗一样。 我们将尝试“达到”他们的中心和高点。 但是那会发生什么呢?
墙后面是什么?
我可能不知道如何,但是我们将解决这个问题。 也许量子或(!)Quark计算机会帮助我们。 但这不会成为墙壁上的孔。 高斯素数和一个更复杂的方程式(可能代表许多素数)可能会进一步等待我们。 然后,也许在其他超复数中,我们将再次遇到某种“简单”行为。 最终,这可能是极限,这是数学黑洞的一种事件视界。
在这种情况下可能是什么? 可能是某种数学上的奇点。 大概,我们将完全了解所有集合的一切,我们将能够解决任何方程式和任何问题。 也许根本不会再有新的问题和任务了?
正是这种想法出现了。 好吧,实际上,您可以问有关质数的任何问题,并且由于这个方程式,您可以得到答案。 双生素数是无限的吗? 求解该方程,进行几次代数计算并获得答案。 以1、3、7或9结尾的质数是什么? 相同的算法:两次计算和方程的替换。 您是否要快速将数字分解为素数?
总结
我在2008年第一次遇到这个方程式,那时我已经对密码学和数论(尤其是RSA方案和因式分解问题)着迷了。 当然,在我看来,生成质数的多项式似乎很有趣,但是太复杂了。 但是,所有可以解决或无法解决的问题都与Diophantine方程有关。 因此,在2014年,我再次转向该多项式,决定简单地连续探索数学的所有部分,并寻找对解决它有用的东西。 当然,我的所有作品都谈不上任何学术文化-我从不保存系统记录,也从未汇总生成的代码。 这只是我的爱好。
我看完电影《星际穿越》后想到了写这篇文章的想法。 我不敢相信黑洞和引力能够如此令人兴奋。 但是,事实证明,“不存在”的数学世界一直给我以相同的印象。 这个世界也有自己无法到达的“深空”和自己的“基本粒子”。
通过这篇文章,我想表明,有可能至少对任何一项最困难,甚至是不可能的任务都有所帮助。 这样的任务很多,您可以选择自己喜欢且最接近感兴趣区域的任务。 当然,过度的复杂性和有保证的失败将剥夺这项工作的丝毫愿望。 但是,整个悖论是,即使在“不存在”的数学世界中,最有趣的旅行和冒险通常都是以此方式开始的。