Geekly articles weekly

StackOverflow历史上最受欢迎的代码有一个错误！

最近的一项研究“在GitHub项目中使用和分配Stack Overflow代码片段”突然发现，在大多数开源项目中，我的答案差不多是十年前写的。 具有讽刺意味的是，有一个错误。

很久以前...


早在2010年，我就坐在办公室里胡说八道：我喜欢打高尔夫球，并为Stack Overflow评分。

以下问题引起了我的注意：如何以可读格式显示字节数？ 也就是说，如何将类似123456789字节的内容转换为“ 123.5 MB”。


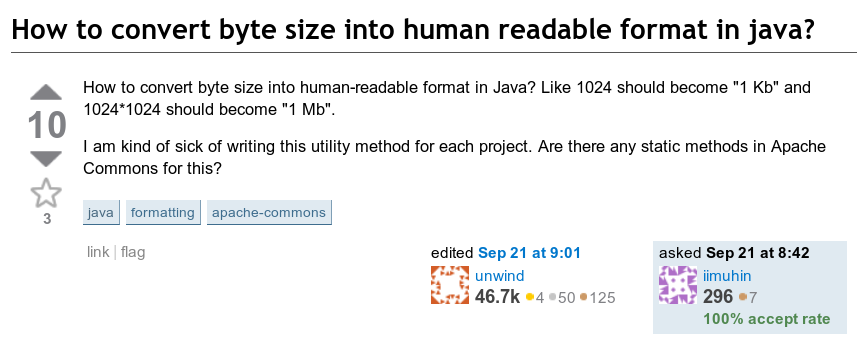良好的2010年旧界面，感谢Wayback Machine

隐式地，结果将是1到999.9之间的数字（具有适当的单位）。

已经有了一个循环的答案。 这个想法很简单：检查从最大单位（EB = 10 18字节）到最小单位（B = 1字节）的所有度数，然后应用第一个小于字节数的度数。 在伪代码中，它看起来像这样：

suffixes = [ "EB", "PB", "TB", "GB", "MB", "kB", "B" ] magnitudes = [ 10^18, 10^15, 10^12, 10^9, 10^6, 10^3, 10^0 ] i = 0 while (i < magnitudes.length && magnitudes[i] > byteCount) i++ printf("%.1f %s", byteCount / magnitudes[i], suffixes[i])

通常，如果答案正确且得分为正，则很难追上它。 在Stack Overflow中，这被称为西方最快射手的问题 。 但是这里的答案有几个缺陷，所以我仍然希望超越它。 至少可以大大减少带有循环的代码。

好吧，这就是代数，一切都很简单！


然后它突然降临在我身上。 前缀为千，兆，千兆，...-仅为1000度（在IEC标准中为1024），因此可以使用对数而不是循环来确定正确的前缀。

基于这个想法，我发表了以下文章：

 public static String humanReadableByteCount(long bytes, boolean si) { int unit = si ? 1000 : 1024; if (bytes < unit) return bytes + " B"; int exp = (int) (Math.log(bytes) / Math.log(unit)); String pre = (si ? "kMGTPE" : "KMGTPE").charAt(exp-1) + (si ? "" : "i"); return String.format("%.1f %sB", bytes / Math.pow(unit, exp), pre); }

当然，这不是很可读，并且log / pow的效率不如其他选项。 但是没有循环，几乎没有分支，所以我认为结果非常漂亮。

数学很简单 。 字节数表示为byteCount = 1000 s ，其中s表示度（以二进制表示，基数为1024。）解决方案s给出s = log 1000 （byteCount）。

API中没有简单的表达式log 1000 ，但是我们可以用自然对数来表示它，如下所示：s = log（byteCount）/ log（1000）。 然后将s转换为int，因此，例如，如果我们有一个以上的兆字节（但不完整的千兆字节），则MB将用作度量单位。

事实证明，如果s = 1，则维度为千字节，如果s = 2-兆字节，依此类推。 将byteCount除以1000 s，然后将相应的字母拍入前缀。

剩下的就是等着看社区如何看待答案。 我不认为这段代码会成为Stack Overflow历史上使用最广泛的代码。

归因研究


快进到2018年。 研究生Sebastian Baltes在科学期刊Empirical Software Engineering上发表了一篇文章，题为“在GitHub Projects中使用和归因于堆栈溢出代码段” 。 他的研究主题是多少尊重Stack Overflow CC BY-SA 3.0许可证，即作者是否将Stack Overflow链接作为代码源。

为了进行分析，从堆栈溢出转储中提取了代码片段，并将其映射到公共GitHub存储库中的代码。 引用摘要：

我们提供了一项大规模实证研究的结果，分析了公共GitHub（GH）项目中来自SO答案的Java代码非平凡片段的使用和归因。

（扰流器：不，大多数程序员不符合许可证要求）。

该文章有这样一个表格：



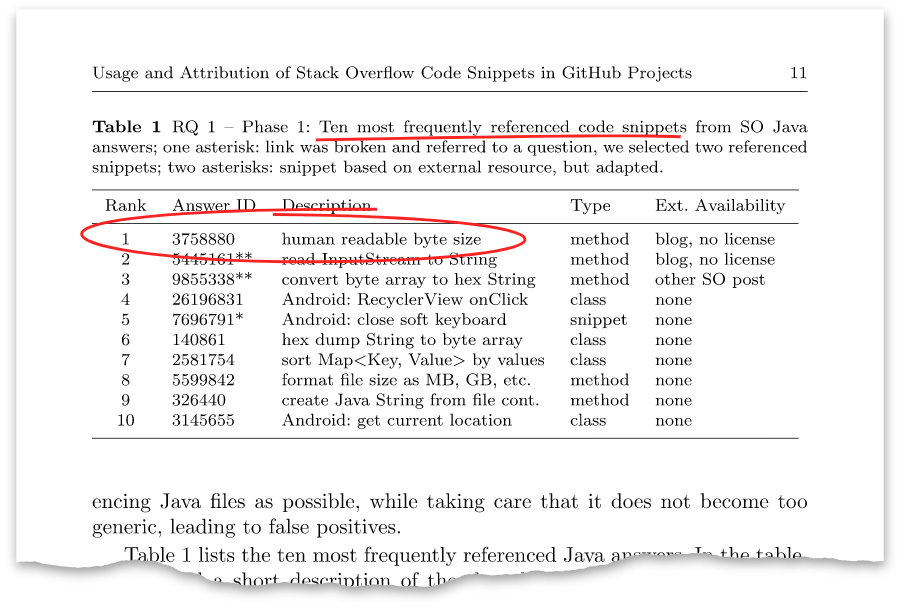
上面带有标识符3758880的答案原来是我八年前发布的答案。 目前，他的浏览量已超过10万，而且有超过一千个优点。

在GitHub上进行的快速搜索实际上使用代码humanReadableByteCount生成了数千个存储库。



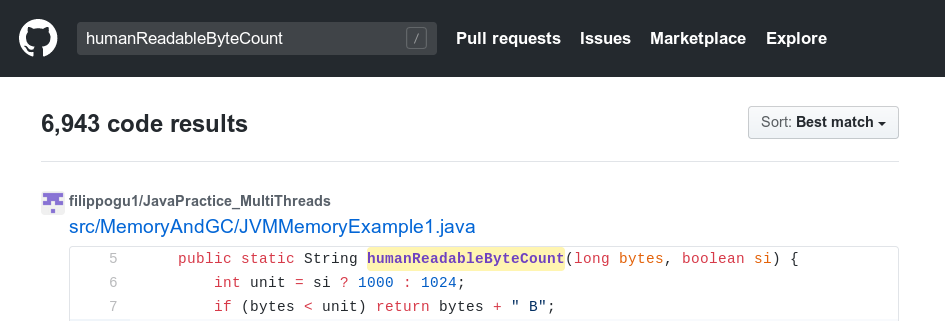
在您的存储库中搜索此片段：

 $ git grep humanReadableByteCount

我发现这项研究很有趣 。

Sebastian在OpenJDK存储库中找到了一个匹配项，没有任何出处，并且OpenJDK许可证与CC BY-SA 3.0不兼容。 在jdk9-dev邮件列表中，他问：是从OpenJDK复制了堆栈溢出代码，反之亦然？

有趣的是，我刚在Oracle的OpenJDK项目中工作，所以我的前同事和朋友写道：

你好

为什么不直接在SO（aioobe）上问这篇文章的作者呢？ 他是OpenJDK的成员，并在此代码出现在OpenJDK源代码库中时在Oracle工作。

Oracle非常重视这些问题。 我知道有些经理在读完此答案并找到“罪魁祸首”后松了一口气。

然后塞巴斯蒂安（Sebastian）给我写信以澄清情况，我做到了： 在加入Oracle 之前添加了此代码，并且与提交无关。 最好不要和Oracle开玩笑。 打开票证后的几天，该代码已被删除 。

虫子


我敢打赌，您已经考虑过了。 代码中出现哪种错误？

再一次：

 public static String humanReadableByteCount(long bytes, boolean si) { int unit = si ? 1000 : 1024; if (bytes < unit) return bytes + " B"; int exp = (int) (Math.log(bytes) / Math.log(unit)); String pre = (si ? "kMGTPE" : "KMGTPE").charAt(exp-1) + (si ? "" : "i"); return String.format("%.1f %sB", bytes / Math.pow(unit, exp), pre); }

有哪些选择？

在EB（10 18 ）之后是Zettabytes（10 21 ）。 也许会有很大一部分超越kMGTPE？ 不行 最大值是2 63 -1≈9.2×10 18 ，因此没有值会超过EB。

可能是SI单位和二进制系统之间的混淆？ 不行 答案的第一版中有些混乱，但很快就解决了。

也许exp最终归零，导致charAt（exp-1）崩溃？ 也不行 第一个if语句涵盖了这种情况。 exp值将始终至少为1。

引渡中可能有一些奇怪的舍入错误？ 好吧，终于...

许多九


该解决方案一直有效，直到接近1 MB。 当指定"1000,0 kB"字节作为输入时，结果（在SI模式下）为"1000,0 kB" 。 尽管999,999比999.9×1000 1更接近1000×1000 1 ，但本规范禁止使用符号1000。 正确的结果是"1.0 MB" 。

为了辩护，我可以说在撰写本文时，所有22个已发布的答案（包括Apache Commons和Android库）中都存在这种错误。

如何解决？ 首先，我们注意到，一旦字节数更接近于1×1,000 2 （1 MB），而不是999.9×1000 1 （999.9 k），则指数（exp）必须从'k'变为'M'。 ） 这发生在999,950。同样，当我们经历999,950,000时，我们应该从“ M”切换为“ G”，依此类推。

我们计算此阈值，如果bytes更大，则增加exp ：

 if (bytes >= Math.pow(unit, exp) * (unit - 0.05)) exp++;

通过此更改，代码可以正常工作，直到字节数接近1 EB。

更多尼尼斯


计算999949949999999999999999时，代码给出1000.0 PB ，正确的结果是999.9 PB 。 从数学上讲，代码是准确的，那么这里会发生什么呢？

现在，我们面临double约束。

浮点算法简介


根据IEEE 754规范，接近零的浮点值具有非常密集的表示，而较大的值具有非常稀疏的表示。 实际上，所有值的一半在-1和1之间，并且当涉及大数时， Long.MAX_VALUE大小的值并不意味着任何东西。 从字面上看。

 double l1 = Double.MAX_VALUE; double l2 = l1 - Long.MAX_VALUE; System.err.println(l1 == l2); // prints true

有关详细信息，请参见“浮点位” 。

该问题由两个计算表示：

  • String.format除法和
  • 扩展阈值exp

我们可以切换到BigDecimal ，但这很无聊。 此外，这里还会出现问题，因为标准API没有BigDecimal的对数。

减少中间值


为了解决第一个问题，我们可以将bytes的值减小到精度更好的所需范围，并相应地调整exp 。 在任何情况下，最终结果都是四舍五入的，因此我们将最低有效位舍去就没有关系了。

 if (exp > 4) { bytes /= unit; exp--; }

最低有效位设置


要解决第二个问题，最低有效位对我们很重要 （99994999 ... 9和99995000 ... 0必须具有不同的度数），因此我们必须找到不同的解决方案。

首先，请注意有12个不同的阈值（每种模式为6个），只有其中一个会导致错误。 由于错误结果以D00 16结尾，因此可以唯一标识错误结果。 因此，您可以直接修复它。

 long th = (long) (Math.pow(unit, exp) * (unit - 0.05)); if (exp < 6 && bytes >= th - ((th & 0xFFF) == 0xD00 ? 52 : 0)) exp++;

由于我们依赖浮点结果中的某些位模式，因此我们使用strictfp修饰符来确保代码独立于硬件运行。

负输入值


目前尚不清楚在什么情况下负数字节可能有意义，但是由于Java没有unsigned long ，因此最好处理此选项。 现在，输入-10000 B会产生-10000 B

让我们写absBytes ：

 long absBytes = bytes == Long.MIN_VALUE ? Long.MAX_VALUE : Math.abs(bytes);

该表达式非常冗长，因为-Long.MIN_VALUE == Long.MIN_VALUE 。 现在我们使用absBytes而不是bytes进行所有exp计算。

最终版本


这是代码的最终版本，本着原始版本的精神进行了简化和压缩：

 // From: https://programming.guide/the-worlds-most-copied-so-snippet.html public static strictfp String humanReadableByteCount(long bytes, boolean si) { int unit = si ? 1000 : 1024; long absBytes = bytes == Long.MIN_VALUE ? Long.MAX_VALUE : Math.abs(bytes); if (absBytes < unit) return bytes + " B"; int exp = (int) (Math.log(absBytes) / Math.log(unit)); long th = (long) (Math.pow(unit, exp) * (unit - 0.05)); if (exp < 6 && absBytes >= th - ((th & 0xfff) == 0xd00 ? 52 : 0)) exp++; String pre = (si ? "kMGTPE" : "KMGTPE").charAt(exp - 1) + (si ? "" : "i"); if (exp > 4) { bytes /= unit; exp -= 1; } return String.format("%.1f %sB", bytes / Math.pow(unit, exp), pre); }

请注意，这开始是为了避免循环和过多的分支。 但是在消除所有边界情况之后，该代码变得比原始版本更具可读性。 就个人而言，我不会在生产中复制此片段。

有关生产质量的更新版本，请参阅另一篇文章： “以可读格式设置字节大小 。 ”

主要发现


  • 即使有数千个加号，Stack Overflow的答案中也可能有错误。
  • 检查所有边界情况， 尤其是在带有堆栈溢出的代码中。
  • 浮点运算很复杂。
  • 复制代码时，请确保包括正确的归因。 有人可能会带您去清洗水。

Source: https://habr.com/ru/post/zh-CN478878/

More articles:


All Articles