引言
本文讨论了组装魔方的“ Y方法”-易于理解和记住。 它仅基于一个序列,称为“ Y运动”。 了解了此算法后,您不太可能会忘记如何自己组装多维数据集。
如果您尝试搜索Rubik's Cube的组装说明,那么会有很多描述“简单组装”的选项,包括
Wikipedia上 。 通常,它们确实很容易理解,但是有一个明显的缺点。 为了组装一个多维数据集,您需要了解五个或更多个非平凡的序列(算法)以重新排列各个多维数据集,以将Rubik的多维数据集组装为层。 就此而言,难以独立记住和再现这些指令。 最近,我无意间偶然发现了提到算法“
魔方的终极解决方案 ”的算法,该算法据称易于记忆和理解,并且仅使用两个序列。 当我开始更详细地查找时,我还发现了另一种算法“
Y方法 ”,该算法也很简单,仅使用一个序列。
不幸的是,我没有用俄语找到对此算法的描述,所以我决定填补这一空白。 在我看来,这种方法的主要目的是了解其工作方式。 因此,在这里我不提供针对特定情况的现成的机芯,而是尝试更详细地描述正在发生的事情。
本文中的图片是使用
ruwix.com上的工具生成的。 图片上的链接将使用与图片对应的参数打开此工具。 这是所描述的多维数据集状态,您可以使用鼠标旋转它,或者在某些情况下,可以在此处指定所描述的移动,这些移动可以来回“丢失”。
Y运动
该算法的基础是Y运动。 该算法的一个相当重要的组成部分是了解这种运动的机理。
之所以称此为转弯顺序,是因为它接触的立方体看起来像字母“ Y”,由三个角从立方体的一个角伸出。

Y运动非常简单,它由两个相邻面(例如,右和前)的四匝组成。 在魔方的通用旋转表示法中,它看起来像这样:R'FR F'。 可以描述如下:
- 右侧逆时针旋转四分之一圈
- 正面顺时针旋转四分之一圈
- 右侧顺时针旋转四分之一圈
- 正面逆时针旋转四分之一圈
也就是说,首先将这些面孔“朝自己”旋转,然后以相反的顺序“从他们”旋转。
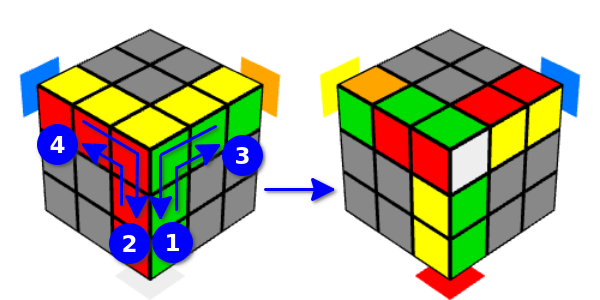
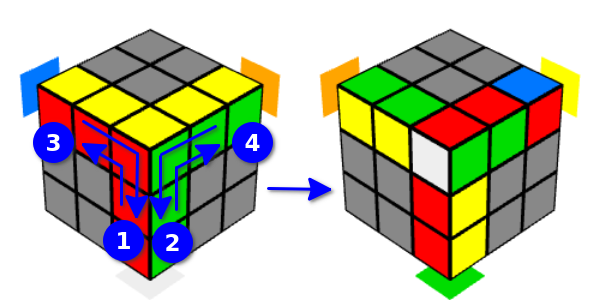
我们将这个选项称为“右Y移动”(因为面部先向右旋转)。 在这种情况下,立方体在边缘上的位置会发生变化,这对于这些面和上边缘来说是常见的。 如果从正面开始转弯,则将影响相同的多维数据集,我们将此选项称为“向左Y移动”(因为先从左侧向正面转弯)。
您也可以从“自己动手”开始转弯-如果我们翻转多维数据集并从“自己转弯”开始转弯也是如此,因此我们将此类选项称为“向右和向左倒Y移动”。 在反转的Y运动下,相邻的边缘也会受到影响,而不是上边缘,而是相邻的下边缘都将受到影响。
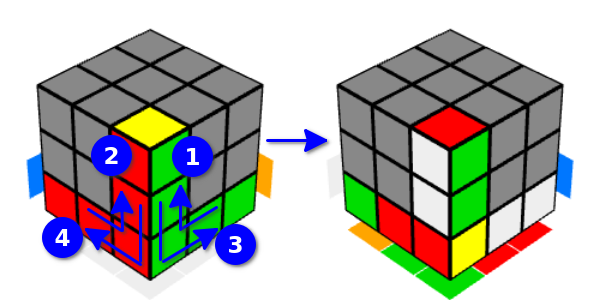
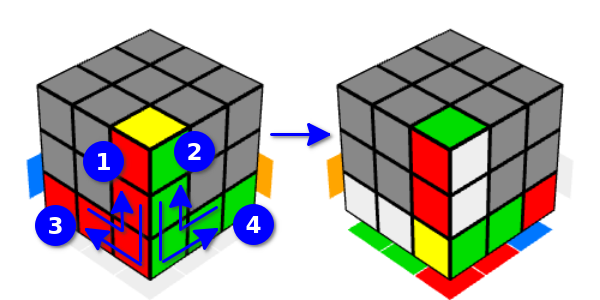
当然,所有这些动作都没有根本的区别。 这样的变化只是为了方便。
我们列出了Y运动的一些属性:
- 左右Y运动彼此相反,即 左右移动或左右移动的顺序不会更改多维数据集的状态。
- 一个Y轴运动会导致相邻面上的两个角形立方体和另外两个角形立方体成对改变位置。 并且位于边缘(边缘)中间的三个立方体成圆周运动。
- 您可能会猜到,经过两次移动后,角corner将返回其位置。 但与此同时,他们被转了身。
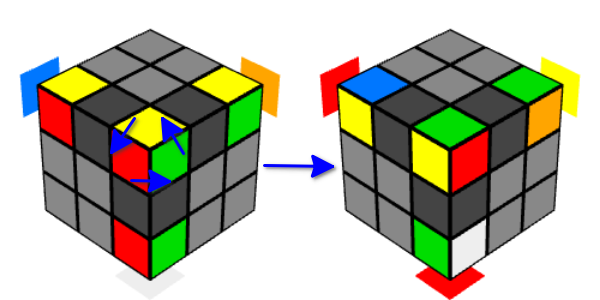
- 而且,如果您两次移动三遍,则多维数据集将旋转三遍,结果将返回其原始状态。
- 经过三个运动周期后,边缘立方体将返回其原始状态。
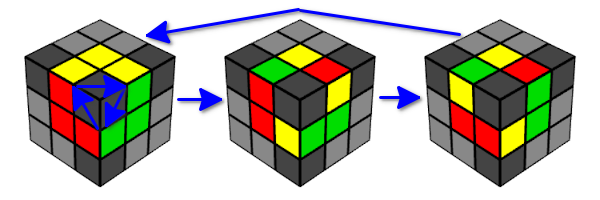
- 因此,如果连续六次执行Y移动,则多维数据集的状态将返回其原始状态。
- 在进行一次Y轴移动后,边角立方体在第一次旋转的方向上运动,而两个立方体似乎沿着相应的面(围绕其轴)旋转,而第三个立方体也旋转,但翻过来。 在通常的(不是反向的)Y移动的情况下,在上边缘之间移动的立方体会翻转。 当使用边缘立方体时,可以通过沿不同方向旋转立方体来执行沿相同边缘的Y移动,从而实现所需立方体的旋转。
多维数据集组装顺序
首先,组装立方体的两个较低层,除了一个垂直边缘穿过这些层。 我们保留这个地方作为回旋的空间。 下部十字和下部角形立方体的组装非常简单,但是如果有困难,则不难采用这种方式来适应Y型运动,也可以参阅其中一个简单的分层立方体组装说明。

接下来,您需要在垂直边缘(边缘)上收集中间的立方体。 为此,用所需的立方体旋转顶面,使其位于与目标边缘相邻的面之一上。 并暂时(不要忘记然后返回该位置)旋转底面,以便代替目标边缘,放置一个我们专门拆开的立方体。 现在,您可以使用Y型移动将立方体从顶面移动到我们需要的位置。 需要进行Y轴移动,以使此棱角立方体沿向右的方向朝向肋骨旋转,并在必要时翻转。

如果所需的立方体不在上表面,则必须事先通过Y形运动从那里“释放”它,而又不要忘记替换下表面上未组装的角。

到目前为止,我们已经收集了两个较低的层而没有一个边缘。 接下来,我们将需要在上边缘收集两个边缘立方体,这两个立方体不与我们未专门收集的边缘相邻。 之后,在形成字母“ Y”的边缘上,仅剩下三个未组装的边缘立方体:我们没有收集到的垂直立方体以及与之相邻的两个上边缘。

而且,当然,我们使用一个或多个Y型运动收集它们,将它们翻转并放置在正确的位置。 在这里,您只需要考虑一刻的排列数量,下面将对此进行介绍。
当组装最后五个边缘立方体时,我们可能需要展开此字母“ Y”以使Y方向朝另一个方向移动(沿这些边缘旋转其他面),从而实现我们需要的立方体在旋转或不旋转的情况下向其他位置的移动。

此时,我们将得到一个几乎组装好的立方体,其中仅不收集未收集的上表面和垂直边缘上的角形立方体。 使用下面描述的方法,我们首先彼此重新排列角度,以使它们位于适当的位置,可能方向不正确。 然后我们部署它们。
万岁,我们的立方体组装好了!
我们考虑排列
当我们收集最后五个边缘立方体时,您需要注意什么。 如果只剩下三个,则为了使所有内容都能在字母“ Y”内进行重新排列,有必要将它们全部放在适当的位置(可能倒置)或全部都不正确。 这是由于以下事实:Y轴运动会同时重新排列三个边缘立方体。 如果我们从相邻边上的立方体的成对交换的角度考虑这一点,那么就有两个交换(置换)。 现在应该清楚为什么,如果我们恰好有两个多维数据集不正确,那么我们将无法收集它们。 因为 我们需要做一个排列,在Y轴运动的帮助下,我们只能做偶数个排列。
在这种情况下该怎么办? 请注意,如果旋转立方体的面,那么我们将同时交换四个边缘立方体,这将等效于三个排列,即 我们需要的是一个奇数。 因此,必须正确地确定顶面的方向,以便我们可以收集最后三个边缘立方体。 如果碰巧最后三个边缘立方体需要一个排列,那么这意味着您需要重新排列已经组装在上表面上相邻位置的两个边缘立方体。
此外,我们可以在组装这五个立方体的前两个立方体之前预先计算将所有五个边缘立方体放置到位所需的排列数量。 如果该数字为偶数,则上限方向正确。 而且,如果很奇怪,则需要将其向任意方向旋转一次。 因此,我们可以立即将这两个骰子放在正确的位置。
使用角落立方体
在组装的最后阶段,我们需要重新放置角形立方体并旋转它们。 为此,我们使用前面提到的关于角corner的Y运动属性。 因为 使用位于上方的角形立方体更方便,为此,我们将使用倒置的Y型移动(从“远离你”开始转弯)。 在本节中,将使用这些选项而无需进一步说明。 让我们立即注意到,该运动仅改变了上表面上一个立方体的状态-这是“相邻边缘”上的一个有角立方体。
要重新排列角cube,我们注意到单个Y动作(左和右)在“相邻边”上交换一对角cube,并且顺序使用左和右Y动作(或右和左)会返回整个立方体在初始状态。 让我们考虑一下如果在这些运动之间旋转顶面会发生什么。 正如我们已经注意到的,在顶面上只有一个角形立方体发生变化,该角形立方体在边缘被重新排列为一对。 在这种情况下,我们将在边缘上交换两次角corner,但每次在顶部替换一个不同的角度时,所有其他角will将保持原样(当然,您仍然必须记住将顶面旋转到其原始状态)。 因此,我们交换了三个角锥的位置-一个从底部到两个从顶部。
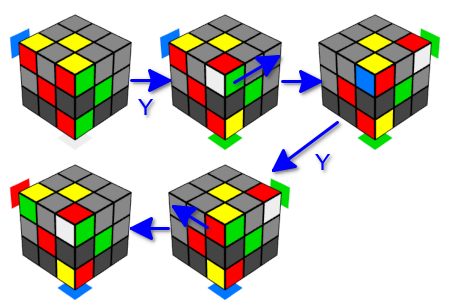
现在,我们将处理多维数据集的旋转。 为此,请使用类似的技巧。 我们将在一个方向上进行两个连续的Y移动。 结果,角cube石保留在原处,但是改变了它们的方向。 在这里,我们对组合运动的两个选项感兴趣:一个方向(左或右)的三个双重运动或一个方向的双重运动和相反方向的双重运动。 在每个选项中,整个多维数据集都将返回其原始状态。 同样,我们将在两次运动之间替换下一个需要的角度来代替“相邻肋骨”的上角。 因此,我们可以在一个面上朝一个方向旋转三个角锥,或者在一个面上朝不同方向旋转两个角锥,而无需更改其余立方体的状态。 注意,在两次移动之后,相邻肋的上立方体沿与执行第一次Y移动相同的方向旋转。
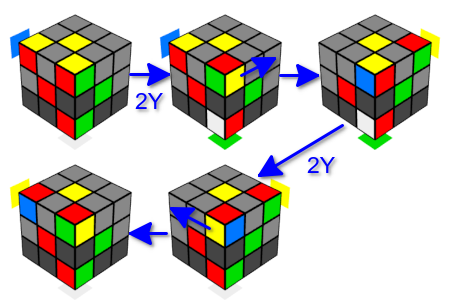
结论
我不知道您的情况如何,但是对我来说,这种算法的优势不仅在于它易于记忆,而且您无需填充汇编说明。 但是,事实上,现在,我要收集多维数据集,我自己组装它,了解正在发生的事情,而不是几乎机械地按照说明进行操作,这更加令人愉快。 我也希望你!