赛后几乎所有的纸牌游戏中,您都需要洗牌。 在我洗牌时,问题总是摆在我面前:“已经足够了吗?” 这是一个严重的问题-我不想花太多时间,而且在收费甲板上玩也不是一件好事。
本文将处理这种情况。

随机播放方式
例如,有很酷的方法来洗牌,浅滩洗牌。

我不知道怎么做,纸板卡也不能像这样洗牌,所以我以一种简单的方式洗牌,看起来像这样:

首先,我将零件与卡座分开,然后将这部分的份额扔到另一侧,然后报告剩余的份额。 根据我的观察,人们完全以这种方式或接近随机方式洗牌。 通常,它可以分为多个部分,但是这些已经很详细了。 在本文中,我们将分析这种改组方法。
什么是随机卡布局?
我想到的第一件事是布局很好,任何一张卡都可能排在第i位。
但这还不够。 例如,如果您割开套牌-将其随机分成两部分并交换它们-那么第一张牌就一样可能是任何一张。 但是同时,这显然是一个不好的布局:每张卡之后(除了几张),都会在“切割”之前放置在其后的同一张卡。 也就是说,玩家将收到“相关”卡片。 如果是傻瓜,一个将被殴打,另一个将被殴打,这并非偶然。
确定良好布局的另一种方法是,在第i + 1位有一张独立于第i位的卡。 您可以这样想象:如果您查看卡片组的顶部卡片,您将无法猜测接下来的卡片。
这种方法也可能存在可以通过考虑大的关节分布来解决的问题,但是对于当前的分析而言,它完全适合我们。
如何衡量布局的“好”
我们将上一场比赛剩下的套牌拿了下来。 我们按顺序编号所有卡。 糟糕的情况是,在编号为i的卡之后在某个地方洗牌之后,出现了编号为i + 1的卡。 因此,我们将衡量洗牌后顺序排列的牌的比例。
def next_stat(a): c_next = 0 c_total = 0 for i in range(len(a)-1): c_total += 1 c_next += a[i] == (a[i+1]-1) return c_next * 1.0 / c_total
很明显,即使是在甲板上摆放得井井有条,有些牌也会随机掉落。 他们的份额平均为1 /(n-1),其中n是套牌中的牌数。
证明E(求和($ a i = a {i + 1} $ for i = 0 ..(n-1))/(n-1))=求和(E($ a i = a {i + 1} $ )for i = 0 ..(n-1))/(n-1)-由于垫子的线性。 期望。
并且由于E($ a i = a {i + 1} $)= 1 /(n-1),所以此表达式=(n-1)* 1 /(n-1)/(n-1)= 1 /(n-1)
结果
根据混合迭代的次数,我们计算一副52张牌中连续几张牌的概率。
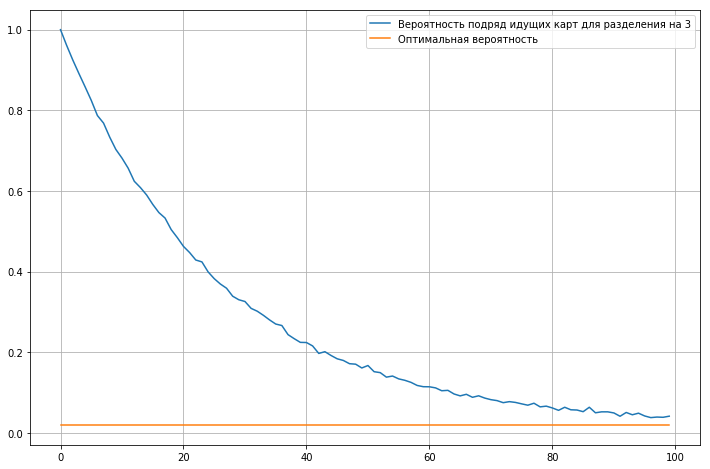
该图显示,即使经过数百次迭代,连续纸牌的概率也比理想概率高大约两倍。
绘图代码 import random def two_split_shuffle(a): s1 = random.randint(1,len(a)-1) s2 = random.randint(1,len(a)-1) s_min = min(s1, s2) s_max = max(s1, s2) p1 = a[:s_min] p2 = a[s_min:s_max] p3 = a[s_max:] return p3 + p2 + p1 def shuffle_n(a, f, n): for _ in range(n): a = f(a) return a def next_stat(a): c_next = 0 c_total = 0 for i in range(len(a)-1): c_total += 1 c_next += a[i] == (a[i+1]-1) return c_next * 1.0 / c_total def expected(f, n = 100): s = 0 for _ in range(n): s += f() return s / n def get_expected_next_stat(shuf, n, cards): return expected(lambda: next_stat(shuffle_n(range(cards), shuf, n))) cards = 52 x = range(100) y = map(lambda i: get_expected_next_stat(two_split_shuffle, i, cards), x) import matplotlib.pyplot as plt %matplotlib inline plt.figure(figsize=(12,8)) plt.plot(x, y, label = u' 3') plt.plot(x, [1./(cards-1)] * len(x), label = u' ') plt.grid() plt.legend()
通常,我们可以假设60次迭代是最佳数量,少则肯定是不好的。 我在30秒内进行了16-17次迭代。 这意味着正常的洗牌大约需要两分钟 。
我和我的朋友从来没有那么多洗牌。 这意味着我们的游戏在很大程度上受到上一游戏平衡的影响。
小心:)