C ++和数值方法：近似牛顿-科茨积分

Newton-Cotes方法是基于以下内容的近似积分技术的组合：

• 将积分间隔分成相等的间隔；
• 多项式在选定间隔上的被积数近似值；
• 找到获得的弯曲梯形的总面积。

本文将介绍几种Newton-Cotes方法：

• 梯形法
• 辛普森的方法；
• 龙伯格法。

梯形法

梯形法是最简单的方法。 例如，采用以下积分：



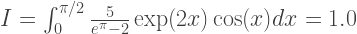
近似精度取决于积分间隔被划分为的段数N。 因此，间隙长度：





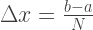
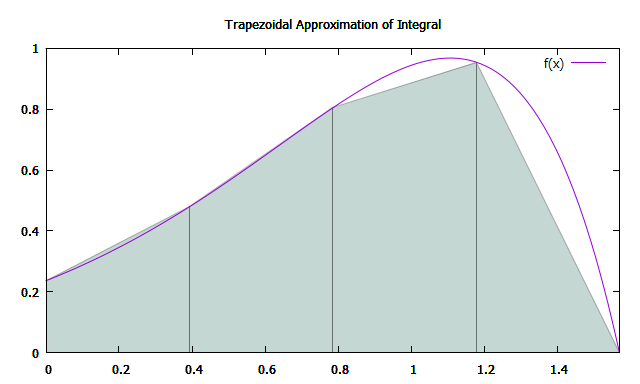
梯形的面积可以通过以下公式计算：



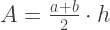
综上所述，积分的近似值由以下公式计算：



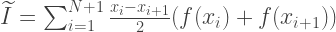
通过梯形法计算积分的函数应采用4个参数：

• 整合部门的边界；
• 积分函数
• 分区的间隔数N。

double trapezoidalIntegral(double a, double b, int n, const std::function<double (double)> &f) { const double width = (ba)/n; double trapezoidal_integral = 0; for(int step = 0; step < n; step++) { const double x1 = a + step*width; const double x2 = a + (step+1)*width; trapezoidal_integral += 0.5*(x2-x1)*(f(x1) + f(x2)); } return trapezoidal_integral; } 

辛普森法

辛普森方法包括将函数f（x）的二次插值多项式与插值节点a，b和m =（a + b）/ 2（抛物线p（x））进行积分。为提高精度，将积分间隔划分为N个相等间隔是有意义的（ （类似于梯形方法），在每个方法上都应用Simpson方法。



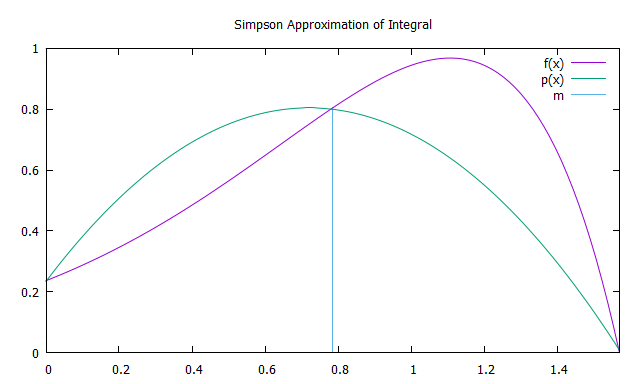
抛物线的面积可以通过将6个等宽的矩形的面积相加得出。 它们中的第一个的高度应等于f（a），从第三到第五的高度-f（m），第六个的高度-f（m）。 因此，Simpson方法的近似值可通过以下公式找到：

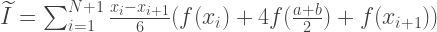
 double simpsonIntegral(double a, double b, int n, const std::function<double (double)> &f) { const double width = (ba)/n; double simpson_integral = 0; for(int step = 0; step < n; step++) { const double x1 = a + step*width; const double x2 = a + (step+1)*width; simpson_integral += (x2-x1)/6.0*(f(x1) + 4.0*f(0.5*(x1+x2)) + f(x2)); } return simpson_integral; } 

龙伯格法

令T（x）为梯形法在步骤x处获得的积分近似值。 我们得到3个这样的近似值，每次计算将步长减小2倍。



现在我们构造一个相对于y轴对称的抛物线，穿过点T（1）和T（1/2），以便推断x趋于0的x值。



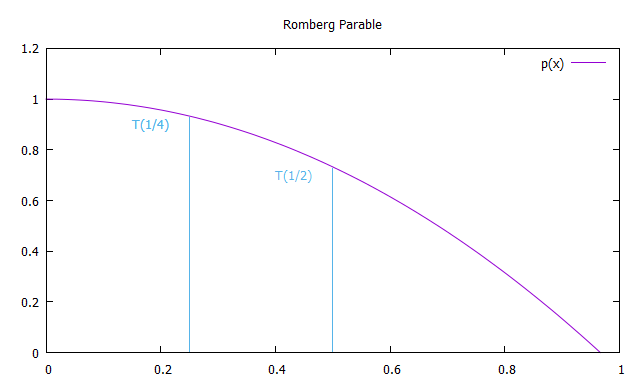
因此，Romberg逼近的第一列R（n，0）的每个成员等于通过梯形方法获得的解，并且R（n，1）的第二列的每个解决方案等效于辛普森方法。 因此，通过Romberg方法进行近似积分的公式为：






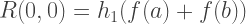
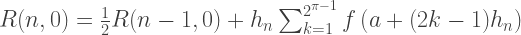
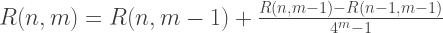
C ++实现：

 std::vector<std::vector<double>> rombergIntegral(double a, double b, size_t n, const std::function<double (double)> &f) { std::vector<std::vector<double>> romberg_integral(n, std::vector<double>(n)); romberg_integral.front().front() = trapezoidalIntegral(a, b, 1, f); double h = ba; for(size_t step = 1; step < n; step++) { h *= 0.5; double trapezoidal_integration = 0; size_t stepEnd = pow(2, step - 1); for(size_t tzStep = 1; tzStep <= stepEnd; tzStep++) { const double deltaX = (2*tzStep - 1)*h; trapezoidal_integration += f(a + deltaX); } romberg_integral[step].front() = 0.5*romberg_integral[step - 1].front() + trapezoidal_integration*h; for(size_t rbStep = 1; rbStep <= step; rbStep++) { const double k = pow(4, rbStep); romberg_integral[step][rbStep] = (k*romberg_integral[step][rbStep-1] - romberg_integral[step-1][rbStep-1])/(k-1); } } return romberg_integral; }