就RGB和色温而言，太空中月亮和太阳的颜色

看来现代科学的太空中的月亮和太阳的颜色问题是如此简单，以至于在我们这个世纪，答案完全没有问题。 我们谈论的是从太空精确观察时的颜色，因为大气会由于瑞利光的散射而引起颜色变化。 您会说：“肯定是在百科全书中的某个地方，有关它的详细信息已经有很长的篇幅了。” 好吧，现在尝试在Internet上搜索有关它的信息。 发生了吗 很可能没有。 您会发现，关于月球的颜色偏淡，而太阳的颜色偏红的事实，您会发现最多。 但是，您将找不到有关这些色彩是否为人眼可见的信息，尤其是RGB或至少色温中的颜色含义。 但是，您会发现一堆照片和视频，其中太空中的月亮绝对是灰色的，大部分在美国阿波罗计划的照片中，太空中的太阳被描绘成白色甚至蓝色。

尤其是我的个人观点不过是政治干预科学的结果。 毕竟，太空中月亮和太阳的颜色直接与美国人飞往月球的飞行有关。

我搜索了许多科学文章和书籍，以寻找有关太空中月球和太阳颜色的信息。 幸运的是，事实证明，即使它们没有直接解决RGB的问题，也有关于太阳辐射的光谱密度和月球在整个光谱中的反射率的完整信息。 这足以获得RGB值中的准确颜色。 您只需要仔细计算实际上我做了什么。 在本文中，我将与您分享计算结果，当然，我将详细介绍计算本身。 您将以真实的色彩看到太空中的月亮和太阳！

我在Mathcad程序中进行了计算，因此，代码片段将使用内置的编程语言，这对于所有伪代码都是可以理解的。

同时，我将详细介绍什么是RGB颜色模型，我认为大家都很熟悉。 这个问题也不是完全简单的。 例如，尝试回答以下两个问题。 让颜色设置为rgb（120,80,100） 。
1）哪些RGB值的颜色比指定的颜色深2倍？
2）与指定亮度相同的灰色RGB值是多少？
似乎在思考，在第一种情况下除以2，即rgb（60,40,50） ，在第二种情况下求平均，即rgb（100,100,100） 。 ，正确的答案是：1） rgb（86.56.71） ; 2） rgb（92.92.92） 。 您会发现为什么答案就是这样。

还讨论色温及其计算方法。

XYZ色彩空间

XYZ是一种主颜色模型，由CIE（国际照明委员会）国际照明组织在1931年从严格的数学意义上定义。CIEXYZ模型是几乎在技术领域中使用的所有其他颜色模型的主模型。 XYZ颜色设置如下：

$$

$$X = \ int _ {390 \，nm} ^ {830 \，nm} I（\ lambda）\，{\上线{x}}（\ lambda）\，d \ lambda \\ Y = \ int _ { 390 \，nm} ^ {830 \，nm} I（\ lambda）\，{\上线{y}}（\ lambda）\，d \ lambda \\ Z = \ int _ {390 \，nm} ^ { 830 \，nm} I（\ lambda）\，{\上线{z}}（\ lambda）\，d \ lambda$$

在哪里 $$$I（\ lambda）$ -在390至830 nm的波长范围内（这是根据2006年的数据，在1931年，此范围从380至780 nm ）; $$${\上划线{x}}（\ lambda）$ ， $$${\上线{y}}（\ lambda）$ ， $$${\ overline {z}}（\ lambda）$ -颜色匹配功能。 此外，对我们而言重要的是，Y坐标对应于信号的视觉亮度。

我从以下位置下载了这些颜色匹配功能： [ 1 ]。 在那里，为2度和10度视场定义了色彩匹配功能。 我决定对这两种情况进行计算，比较结果，并确保如人们所料，颜色坐标略有不同。 自然地，我以提供的最大分辨率（即0.1 nm的步长）使用函数的数据。 颜色匹配函数的图形如下：



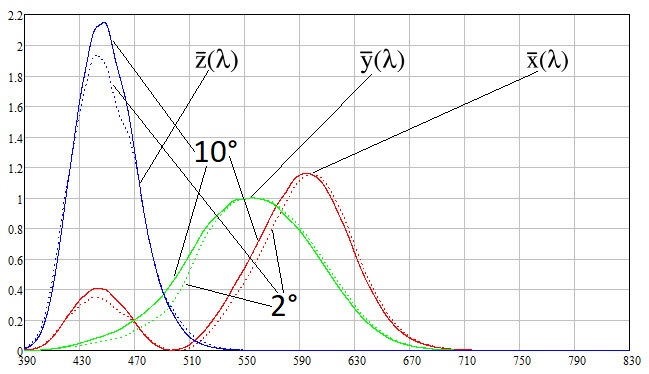
从图中可以看出，在710 nm以上的位置，在观察接近白色的颜色时，在710 nm以上的范围内的光谱密度几乎没有贡献，因此该功能可以忽略不计。 尽管我们知道可见光在780 nm范围内，但是我们必须了解这是单色辐射。 我有一个事实，那就是在计算中我不得不在某些情况下推断出缺失的月球反射率数据，而只是针对色彩匹配功能很小的范围。 因此，可能的外推误差不会导致计算出的颜色出现明显的误差。

我通过梯形法则计算上述积分：


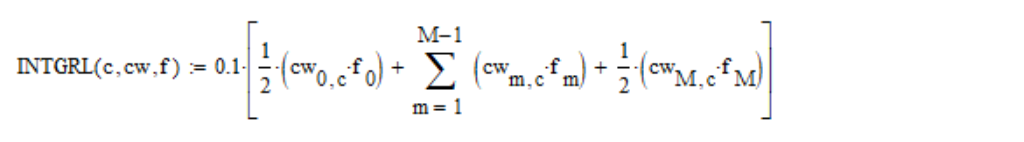
其中c-是色彩空间的坐标号（分别为X，Y，Z为1、2、3）； cw-是色彩匹配功能表； f-光谱密度； M =（830-390）/0.1=4400-网格步数。

正确的色彩匹配功能具有以下所有属性：所有三个曲线下的面积都相同：

$$

$$\ int _ {390 \，nm} ^ {830 \，nm} \，{\上划线{x}}（\ lambda）\，d \ lambda \，= \ int _ {390 \，nm} ^ {830 \，nm} \，{\上划线{y}}（\ lambda）\，d \ lambda \，= \ int _ {390 \，nm} ^ {830 \，nm} \，{\上划线{z}} （\ lambda）\，d \ lambda$$

这样做是为了使均匀光谱具有相同的XYZ坐标值。 检查此属性是否成立：


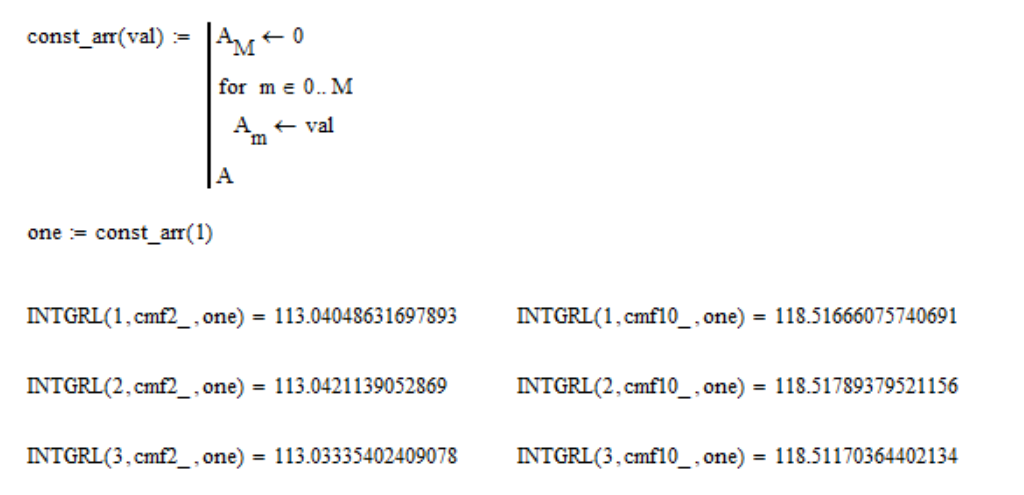
其中“一个”-是1的数组； cmf2_和cmf10_-分别是2度和10度视野的颜色匹配功能表。 如您所见，该属性的执行精度约为0.01％ ，这非常好。 但是，仍然要对功能进行规范化：

亮度归一化

考虑一下数码相机的工作。 数码相机的主要元素是矩阵，由光传感器组成。 当图像投影到矩阵上时，电荷在其每个光电传感器中累积，该电荷与光电传感器的辐射能成比例。 光电传感器捕获图像元素的亮度，而不携带任何有关其颜色的信息。 有关颜色的信息，微型过滤器覆盖在顶部的光电传感器矩阵。 这些滤镜执行颜色匹配功能。 每个像素由几个光电传感器组成，这些光电传感器以各种滤光器的数量组合在一起。

因此，根据功能 $$$I（\ lambda）$ 我们应该取一个像素的辐射能量的光谱密度。 这样的光谱密度可以表示为

$$

$$I（\ lambda）= coef \ cdot照明度（\ lambda）\ cdot反照率（\ lambda）$$

其中照明度 -是光源的光谱密度 ； 反照率 -被摄物体表面的反射 率 ; coef-是一定的常数，由曝光时间，光圈，从光源到要拍摄的物体的距离以及其他因素决定。 反射率是指可见的反照率 ，其定义为平行光线所照射的平面元素的亮度与垂直于光线的绝对白色表面的亮度之比。

现在想象一下，我们正在做光度计的工作，摄影师用它来设置相机的快门速度和光圈。 换句话说，我们需要选择一个coef值，以使图像的亮度正常，不要太暗，不要太亮。 想象一下，在被摄物体的背后有一块绝对是白色的屏幕。 根据定义，这种屏幕的反射率在所有波长下均等于1。 设置coef的值，以使此屏幕的视觉亮度Y等于1。为什么是1？ 因为在RGB颜色模型中，最大可能的亮度值为1，这是通过rgb（255,255,255） ，即白色获得的。 我待会再讲。 由于正常主体的颜色比绝对白色的屏幕要暗，因此图像的亮度将是正常的。 基于这些考虑，我们得到coef的以下表达式：

$$

$$coef = \ frac {1} {\ int _ {390 \，nm} ^ {830 \，nm}光照（\ lambda）\，{\上划线{y}}（\ lambda）\，d \ lambda}$$

应该注意的是，这样的归一化不能保证每个RGB坐标的值都小于或等于255。例如，如果用红色光源拍摄绝对白色的屏幕，则RGB颜色将熄灭。规模。

因此，我按如下方式计算XYZ颜色空间的坐标值：


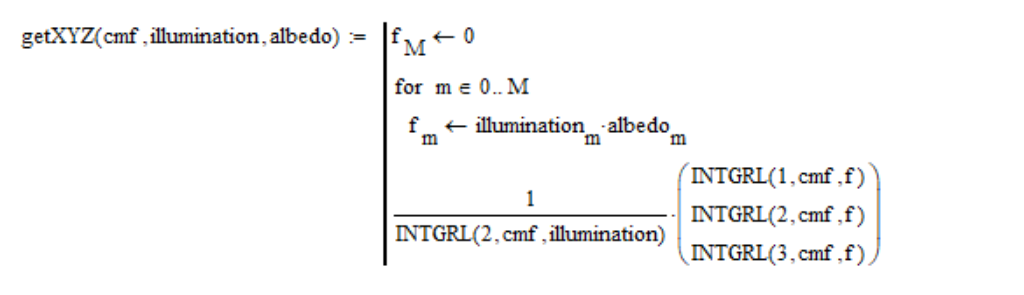
我们需要以某种方式表达太阳的颜色。 我们无法直接拍摄它，在我们的数学模型中，我们没有预见到这种极端情况。 显然，我们需要拍摄太阳照射下的绝对白色的表面。 由于来自太空的太阳具有淡红色调，因此，正如我所说，绝对白色的屏幕的颜色超出了范围。 因此，我们必须使表面变暗。 我凭经验发现，我们必须拍摄白度为0.91的白皮书。 更多反照率无法获取，开始超出范围。 因此，为了获得太阳的颜色，我只需在上述公式中将所有波长的反照率值设置为0.91：

sRGB色彩空间

使用RGB模型的最常见色彩空间是sRGB。 因此，当他们不加说明地谈论RGB时，sRGB颜色空间是使用RGB模型表示色谱的标准。 该标准由国际色彩协会（ICC）于1996年创建，目的是统一在监视器，打印机和Internet站点中使用RGB模型。 让我们分析这个标准，其描述可在[ 2 ]中找到。

XYZ到sRGB的转换分为三个阶段。 首先，将XYZ坐标转换为线性RGB坐标，然后将线性坐标转换为非线性RGB坐标，最后将非线性坐标转换为8位RGB坐标，事实上，这是坐标的坐标。 sRGB色彩空间。

XYZ坐标到线性RGB坐标的转换如下：



而相反的是：



我想知道这些奇怪的数字是从哪里来的？ 它们来自ITU-R BT.709 [ 3 ]的建议。 用XYZ_to_RGB表示第一个方阵，用RGB_to_XYZ表示第二个方阵 。 显然，它们是相互相反的。 ITU-R BT.709建议书规定了对第二矩阵的要求。 根据这些要求，您可以唯一地计算第二个矩阵，并且第一个等于第二个矩阵的逆矩阵。

我们介绍以下功能：

$$

$$XYZ（R，G，B）= RGB \ _to \ _XYZ \ cdot {\开始{bmatrix} R \\ G \\ B \ end {bmatrix}} \\ W（R，G，B）= XYZ_1（R ，G，B）+ XYZ_2（R，G，B）+ XYZ_3（R，G，B）\\ xy（R，G，B）= \ frac {1} {W（R，G，B）} \ cdot {\开始{bmatrix} XYZ_1（R，G，B）\\ XYZ_2（R，G，B）\结束{bmatrix}}$$

然后，ITU-R BT.709建议书的要求采用以下形式：

$$

$$xy（1,0,0）= {\开始{bmatrix} 0.64 \\ 0.33 \结束{bmatrix}}，\; xy（0,1,0）= {\开始{bmatrix} 0.30 \\ 0.60 \结束{bmatrix}}，\; xy（0,0,1）= {\开始{bmatrix} 0.15 \\ 0.06 \结束{bmatrix}} \\ xy（1,1,1）= {\开始{bmatrix} 0.3127 \\ 0.3290 \ end {bmatrix }}$$

当我们有RGB_to_XYZ矩阵的9个未知元素时，我们有8个方程， 即缺少一个方程。 遗漏的方程式是隐式给出的，我必须自己猜一下。 该方程式的实质是，对于白色，视觉亮度Y应等于1：

$$

$$XYZ_2（1,1,1）= 1$$

我找到了这些方程有理数的精确解：


如果将我的结果中的数字四舍五入到小数点后四位小数，您将获得国际色彩协会标准中的那些怪异数字。 在计算中，我没有使用四舍五入的矩阵，而是使用了上面提到的精确矩阵（就双精度浮点数而言）。

因此，基于颜色匹配函数（cmf），光谱辐射密度（照度）和反射率（反照率）的表，RGB的线性坐标计算如下：



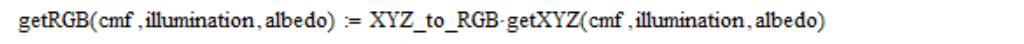
我还使用在2度和10度视场上平均的线性坐标RGB：



根据RGB的线性坐标，使用以下公式计算视觉亮度Y（默认情况下，Mathcad数组从零元素开始编号）：


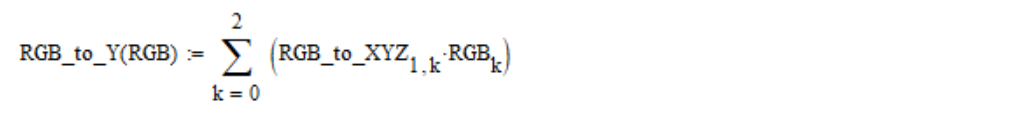
我们继续拆卸标准。 使用非线性函数lin2bit将RGB的每个线性坐标转换为非线性，然后转换回bit2lin，其定义如下：


这些函数的图形如下所示：



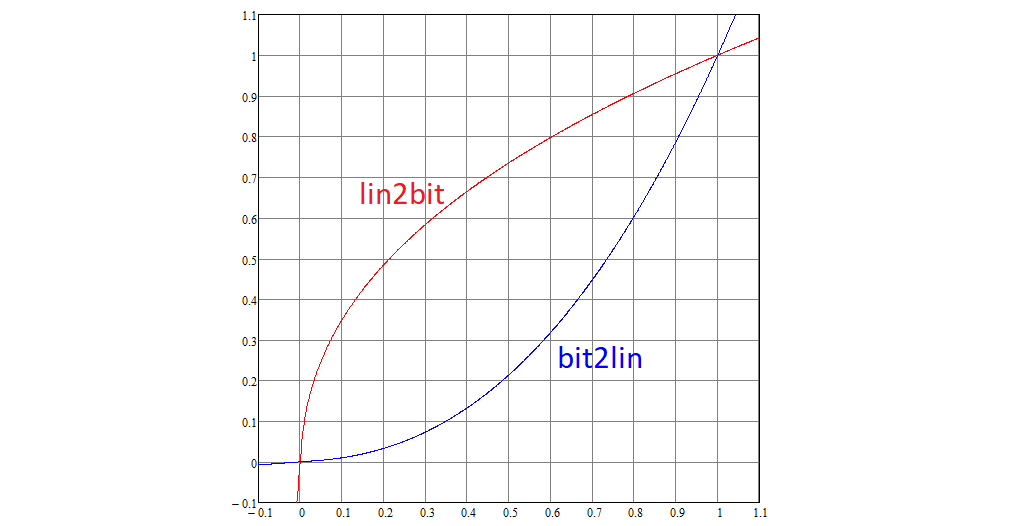
请注意，0转换为0，1转换为1。

最后，RGB的非线性坐标通过乘以255转换为8位，然后四舍五入为整数。

因此，我定义了以下函数，用于将线性RGB坐标转换为8位并返回：

现在我们准备从引言中解决问题。 我提醒情况。

让颜色设置为rgb（120,80,100） 。
1）RGB颜色比指定颜色深2倍的RGB值是多少？
2）与给定亮度相同的灰度的RGB值是多少？

解决方案：

答案：1） rgb（86.56.71） ; 2） rgb（92.92.92） 。

色温

光源的色温 （以开尔文（Kelvin）度量）由位于色卡上与所考虑的辐射源位于同一位置的黑体的温度确定。 如果光源没有落在普朗克曲线上（该曲线由在不同温度下黑体的色点集确定），则将使用相关色温对其进行表征。 该值也用开尔文测量，该温度由黑体的温度确定，黑体的颜色应尽可能接近光源的颜色。 为了在以（u，v）坐标构造的色表上找到辐射源的相关色温，确定普朗克曲线上最靠近辐射源的点（即最短的几何距离）。 此时黑体的温度将对应于所考虑光源的相关色温[ 4 ]。

对于温度为T的黑体，在单位波长间隔内辐射表面每单位面积的辐射功率用普朗克定律表示：

$$

$$R（\ lambda，T）= \ frac {2 \ pi h c ^ 2} {\ lambda ^ 5} \ frac {1} {e ^ {h c / \ lambda k T} -1}$$

因此，我按以下方式计算黑体辐射的光谱密度（在cmf2颜色匹配函数表的零列中为纳米的波长值）：



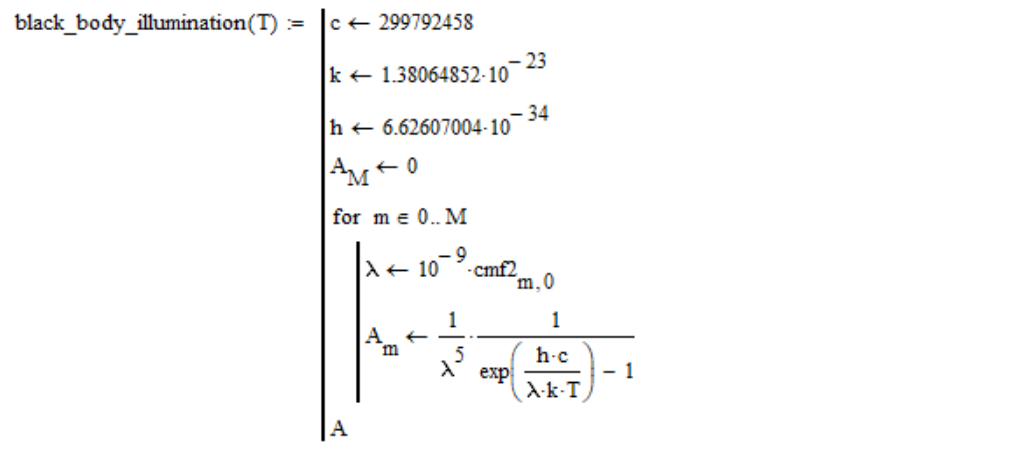
请注意，我跳过了恒定因子，因为随着亮度的进一步标准化它仍然会减小（光源的亮度不会影响色温）。

然后，我计算RGB的线性坐标：



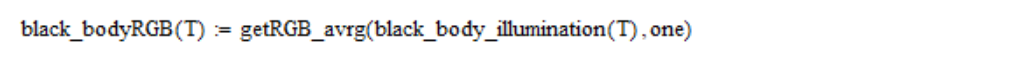
RGB线性坐标转换为（u，v）坐标，如下所示：



在平面（u，v）上 ，计算考虑的颜色的点与给定温度T的黑体的颜色之间的几何距离：



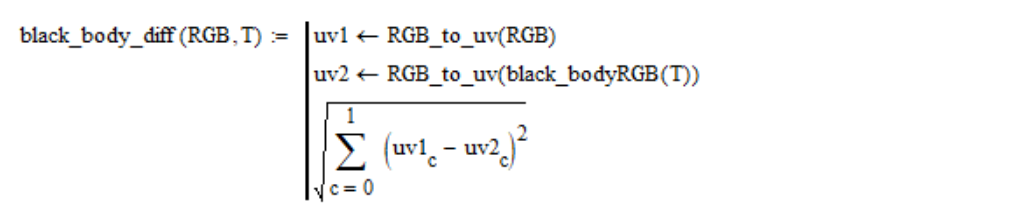
例如，对于标准白光源，此距离对温度的依赖性如下所示：



这种依赖性最小的T值是所考虑的光源的色温。

太阳的辐射光谱密度

我从这里下载了在没有大气的情况下太阳辐射的光谱密度数据： [ 5 ]。 来自太空的与太阳相对应的光源，将来我将称为E490。 为了进行计算比较，我考虑使用标准光源D65 。 该光源代表白光。 我看它是为了显示如果太阳是白色的月亮会是什么样子。 从此处下载的标准光源D65 I的辐射光谱密度数据： [ 6 ]。

如下所示，光源D65和E490的色温分别为6467K和5912K。 光源D65，E490和相应温度的绝对黑体的光谱辐射密度如下：



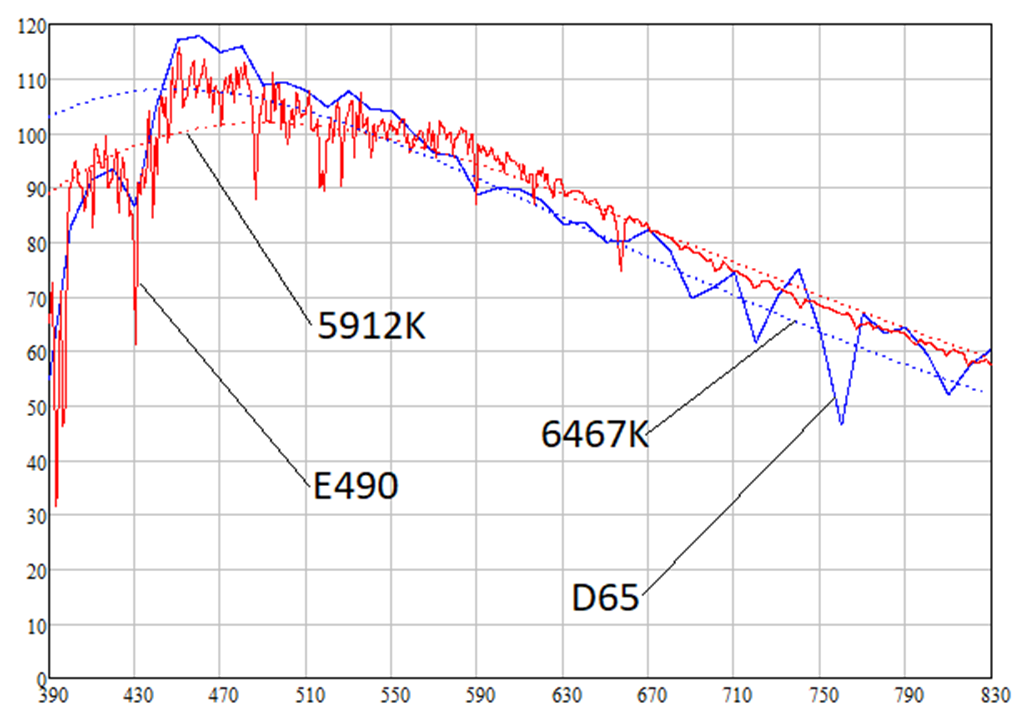
您可以看到，在更长的波长（即在红光的波长（620-770 nm））下，太阳辐射的光谱密度高于白光源的光谱密度。 这意味着太阳具有淡红色的色调。 实际上，计算得出了光源D65，E490和对应温度的黑体的以下颜色（正如我所说，认为反射率为0.91的白皮书）：



请注意，太阳的sRGB和黑体温度5912K的坐标完全匹配。 这没有任何解释，只是发生了。

最后一张图中的圆圈的颜色是太空中太阳的真实颜色。 人眼清楚地看到了太阳的红色调。 因此，来自太空的太阳是白色的事实是一个很大的神话！ 应该注意的是，由于某种原因，在阿波罗照片和视频上没有观察到这种色彩。 在真实照片中，可见的红色调肯定会出现在美国国旗和太空服的白色表面上。 如下所示，太阳的这种颜色对太空中月亮的“红色”做出了重要贡献。

月亮是不同的还是相同的颜色？

阴谋论的反对者提出了月亮颜色不同的说法。 据称，月亮在某些地方是灰色的，在某些地方是棕色的，而阿波罗号则在月亮是灰色的地方着陆。 但是此版本直接与科学数据相矛盾。 文章[ 7 ]明确指出：

月球上的颜色差异非常小。

舍甫琴科还在他的书中写道[ 8 ]：

多年来，美国著名的研究人员T. McCord一直朝着这个方向努力。 他获得了月球表面各部分10-20 km的200多个光谱。 获得的所有曲线在外观上基本相似。

所以，不，月亮的颜色没有不同，但相同。

颜色数据根据舍甫琴科

舍甫琴科在他的书中[ 8 ]给出了反射率对波长的以下依赖性。



在计算中，我应用了该数据的分段线性插值。 我通过在690-820 nm间隔上直接继续该段接收到了在820-830 nm间隔上的丢失数据。

颜色数据符合LRO

在[ 9 ]中给出了月球表面反射率对照明条件和观察条件的依赖性，该条件在321nm至689nm的波长范围内。 模型参数是基于对“月球侦察轨道器”（LRO）所获得数据的分析而计算的。 照明和观察条件由三个参数i （入射角）， e （反射角）和g （相位角）确定。 下图显示了这些角度：



相角可以用方位角表示 $$$\ varPsi$ 使用余弦的球面定律如下：

$$

$$g = \ arccos \左（\ cos \左（i \右）\ cos \左（e \右）+ \ sin \左（i \右）\ sin \左（e \右）\ cos \左（ \ varPsi \ right）\ right）$$

在计算中，我采用了传统的角度值i = g = 30°， e = 0°。 对于这样的角度，可以获得反射率对波长的以下依赖性（图lro30）：


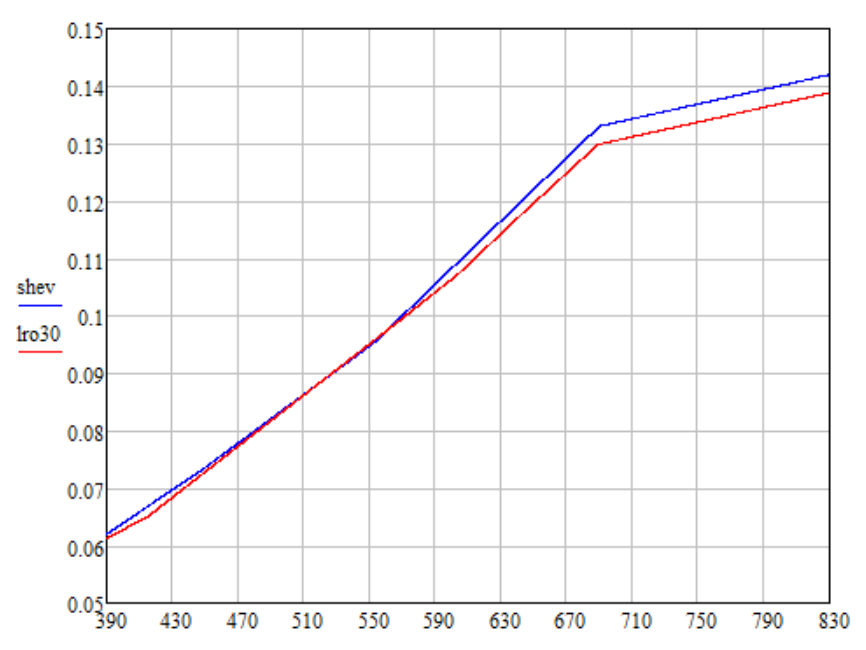
我对LRO数据在689-830 nm的范围内进行了线性外推，以使830 nm和689 nm点处的值之比与Shevchenko数据（谢夫图）相同。 我还对Shevchenko的数据进行了标准化处理，方法是乘以0.8315，以使根据Shevchenko和LRO得出的颜色亮度相同。

根据“ Kaguya”的颜色数据

在[ 10 ]中，介绍了由日本第二颗月球人造卫星获得的数据。 不幸的是，可见光波长范围内的反射率分辨率很低，因此在计算中不使用它。

但是这项工作很有趣，因为它谈到了Kaguya数据与Apollo 16任务数据之间的巨大差异。 这是科学界公开谈论与美国人飞往月球有关的前后矛盾的罕见情况之一。

计算结果

此外，我将使用以下表示法：
D65-标准白光源D65；
E490-在没有大气层的情况下来自太阳的光源；
W-0.91-具有反照率0.91的白皮书；
LRO（30°） -传统角度的LRO数据i = g = 30°， e = 0°；
谢夫 -舍甫琴科的数据；
林 （2°） -具有2度视野的RGB线性坐标；
林 （10°） -RGB的线性坐标，具有10度视野；
林 （平均） -线性坐标RGB，在2度和10度视野中取平均值；
sRGB（100％） -sRGB的坐标，从线性坐标RGB获得，在2度和10度视场中取平均值；
sRGB（200％） -sRGB的坐标，从RGB的两倍线性坐标获得，在2度和10度视场中取平均值；
sRGB（300％） -sRGB的坐标，从RGB的三重线性坐标获得，在2度和10度视场中取平均值；
sRGB（400％） -sRGB的坐标，从RGB的四倍线性坐标获得，在2度和10度视场中求平均值；
cl。 温度 -从RGB线性坐标获得的色温，在2度和10度视野中取平均值；

D65

	W-0.91	LRO（30°）	谢夫
林 （2°）	0.9076,0.9120,0.8968	0.1177,0.0931,0.0688	0.1202,0.0931,0.0697
林 （10°）	0.9084,0.9122,0.8929	0.1165.0.0916.0.0687	0.1188,0.0917,0.0696
林 （平均）	0.9080,0.9121,0.8948	0.1171,0.0924,0.0688	0.1195,0.0924,0.0697
sRGB（100％）	RGB（244,245,243）	RGB（96.86.74）	RGB（97.86.75）
sRGB（200％）	--	英镑（133,119,104）	英镑（134,119,104）
sRGB（300％）	--	RGB（160,144,125）	RGB（161,144,126）
sRGB（400％）	--	RGB（182,164,143）	人民币（184,164,144）
cl。 温度	6467千	4928千	4891千

E490

	W-0.91	LRO（30°）	谢夫
林 （2°）	1.0005,0.8892,0.8490	0.1283.0.0909.0.0649	0.1310,0.0909,0.0657
林 （10°）	1.0021,0.8888,0.8483	0.1272.0.0895.0.0650	0.1297.0.0895.0.0659
林 （平均）	1.0013,0.8890,0.8486	0.1277,0.0902,0.0649	0.1303.0.0902.0.0658
sRGB（100％）	RGB（255,242,237）	RGB（100.85.72）	RGB（101.85.73）
sRGB（200％）	--	英镑（138,118,101）	英镑（140,118,102）
sRGB（300％）	--	RGB（166,142,122）	RGB（168,142,123）
sRGB（400％）	--	RGB（189,162,139）	RGB（191,162,140）
cl。 温度	5912K	4550千	4512K

下图显示了使用E490光源（例如，当何时）时 ，月球的表面颜色sRGB（100％） ， sRGB（200％） （两倍亮度）， sRGB（300％） （三倍亮度）， sRGB（400％） （四倍亮度）从太空观察），根据LRO和Shevchenko。



如您所见，根据LRO数据和舍甫琴科的数据，太空中的月球均为棕色。 舍甫琴科原来比LRO稍微红一点（非常明显）。

照片中的月亮颜色

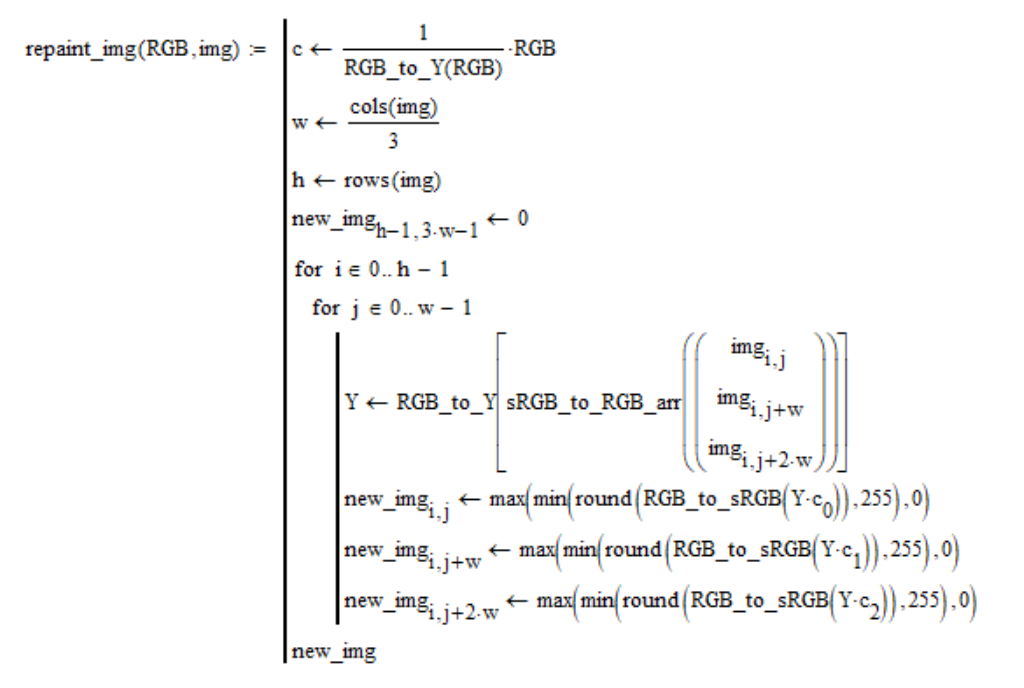
在本节中，我们将为照片着色。 给出图像img和线性坐标RGB中的颜色。 图像的每个像素都被给定颜色的像素替换，该像素的亮度与源像素的亮度相同。 Mathcad程序中的图像表示为单个sRGB坐标矩阵，该矩阵通过从左到右缝合三个“ R”，“ G”，“ B”矩阵获得。 考虑到这一点，着色过程如下：

出于兴趣，我拍摄了描述美国程序月球表面的阿波罗相册照片，并用从计算中获得的颜色进行了重新粉刷。 我只给出结果，并得出结论，这些真实的照片或假照片都是您自己制作的。

图片AS11-44-6552着色的结果：



中间是原始照片。 根据舍甫琴科的数据，在左侧，按照LRO数据以传统角度i = g = 30°， e = 0°为照片上色，而在右侧，则将照片涂成彩色。 第一行对应于标准光源D65，即第一行显示了月球表面的颜色，如果太阳是白色的话，该颜色将获得。 最下面一行对应于光源E490，即最下面一行显示从太空看到的月球表面的自然色。

如您所见，太阳的红色调对月球表面的“红色”做出了重要贡献，月球表面最终看起来是棕色的，而根本不是灰色的。

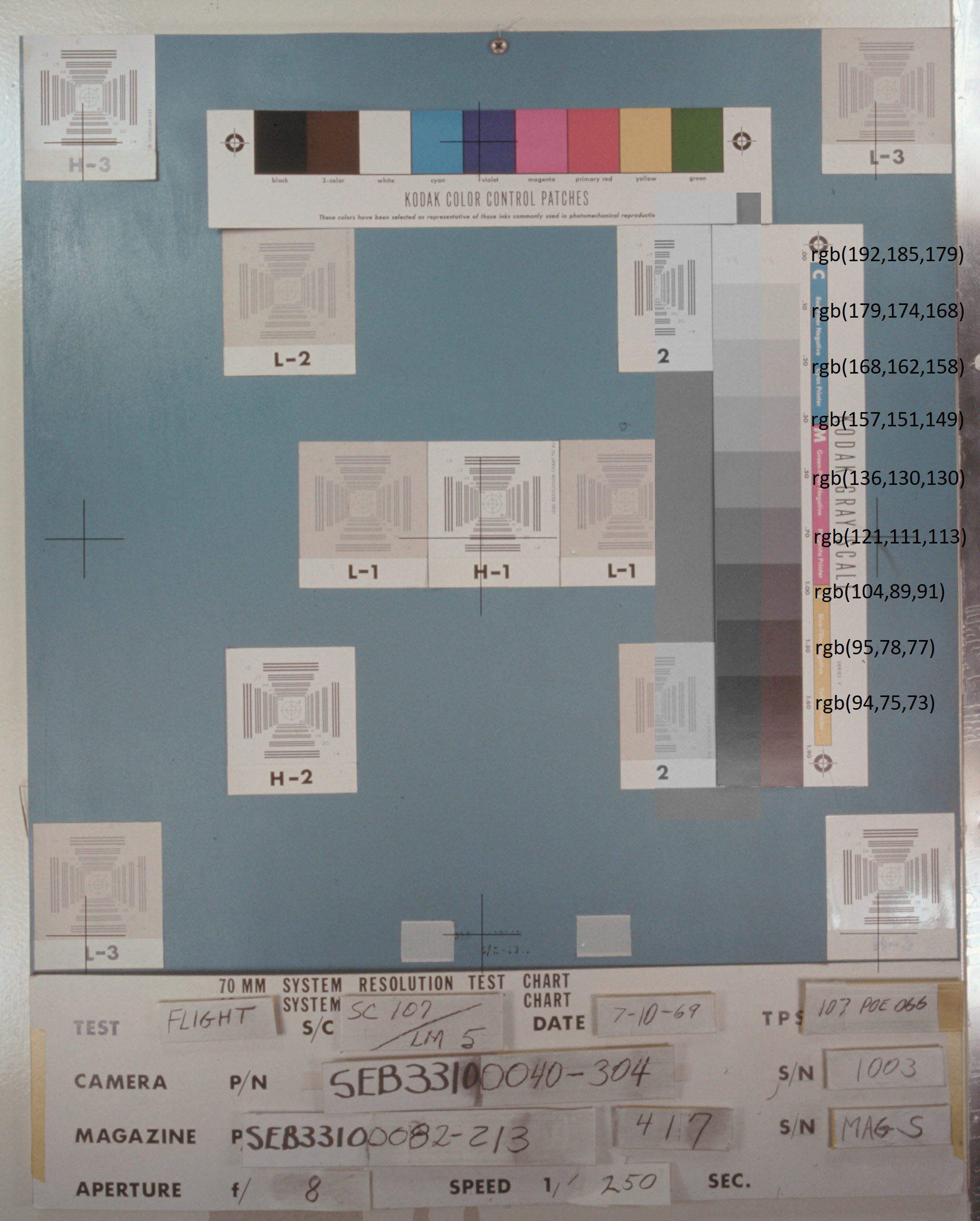
NASA照片中月亮的灰色可以用以下事实来解释：由于某种原因，电影“消失了”变成蓝色，但是如果我们分析相册末尾的灰色渐变图片，则该版本会立即消失。 照片as11-44-chart显示了上面最后一张照片的快照。 我将亮度与照片中相同的真实灰色放置在灰色渐变的左侧，并写下了sRGB坐标值。 结果是以下图像：



如您所见，这部电影不仅没有以蓝色“消失”，甚至在与蓝色相反的方向上稍微“消失”了。 这样的偏差不能变成棕色到灰色。

彩色照片AS11-40-5903的结果：



在原始照片中，某些地方的月球表面不仅呈灰色，甚至略带蓝色。 图片as11-40-chart显示了相应的灰色渐变图片：



电影“消失了”，不是“蓝色”，而是“红色”。 甚至在那之后，由于某种原因，NASA照片中的月球表面还是灰色的。

彩色照片AS11-37-5455的结果：



这是“ Apollo”程序的罕见照片之一，月球表面虽然没有完全着色，但具有棕色。 他们说，阴谋论的反对者喜欢把它展示出来，看起来是棕色的。 但是the俩已经悄悄出现在这里。 让我们分析照片as11-37-chart ，其中显示了相应的灰色渐变图片：



这部电影只是棕色的“左”。 这就是NASA照片中月球表面呈褐色的全部原因。

月球表面颜色对照明和观察条件的依赖性

使用[ 9 ]中给出的LRO数据，我们研究了月球表面的颜色如何随光照和观察条件而变化。 考虑光源E490（来自太空的太阳）和不同的角度i ， e ， $$$\ varPsi$ 。 下图显示了结果，其中上排是具有三倍亮度的颜色，而下排是减小到相同亮度Y = 0.5的颜色。



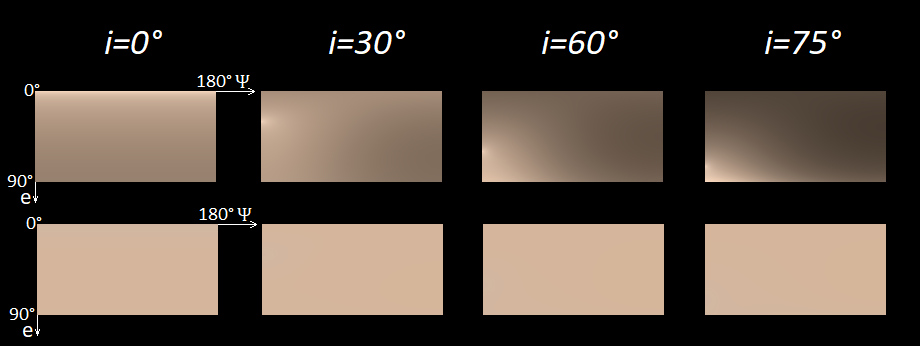
从图片可以看出，只有亮度发生变化。 在最下面一行中，人眼到处的颜色几乎相同。 尽管如果仔细观察，在i = 0°的情况下，当e接近零时，您会看到灰度方向上的非常微小的偏差。

月亮土色

NASA网站上有一张非常奇怪的照片，即这张月球土壤样本No.1的照片。 10005 。



考虑到照明是由白色光源产生的，照片上的月球土壤看起来是棕色，甚至太棕色。 白平衡的正确性可以通过放入框架的白皮书的颜色来检查。

也许这与阿波罗17号宇航员发现的橙色地面相同？ 不行 文件[ 11 ]明确指出，该样品是由阿波罗11号宇航员采集的。

现在让我们听听尼尔·阿姆斯特朗（阿波罗11号宇航员）在1970年对帕特里克·摩尔[ 12 ]的采访中所说的话。

当您近距离查看材料时，就像在您的手中一样，您会发现它实际上是木炭灰色，而我们永远找不到任何与该颜色完全不同的东西。

事实证明，尼尔·阿姆斯特朗（Neil Armstrong）不惧怕这个谎言。

文学作品

1。 色彩与视觉研究实验室-从CIE（2006）LMS功能转变而来的新CIE XYZ功能
2。 国际色彩协会-互联网的标准默认色彩空间：sRGB
3。 ITU-RBT.709建议书-用于生产和国际节目交换的HDTV标准的参数值
4。 RobertsonR。“相关色温和分布温度的计算”。 Soc。 Am.58，1528（1968）。
5， 2000 ASTM标准地球外光谱参考E-490-00
6。 CIE标准光源D65
7 “确定月球土壤的物理机械性能的第一个结果”，M。：1970年。 教授 博士 技术 科学VG Bulycheva，第2 8.（“确定月球土壤的物理机械特性的第一个结果”，M。：1970年。苏联的Gosstroy，由Dr. Sc。
8。 舍甫琴科VV，《月球及其观测》，1983年，第11页。 91-92。 （舍甫琴科诉V.V.，《月亮及其观察》，1983年，第91-92页。）
9。 Hapke，B.，B.Denevi，H.Sato，S.Braden和M.Robinson（2012），月球相位曲线的波长依赖性，如月球侦察轨道飞行器广角相机所见，J。 决议117，E00H15
10。 大竹 等。 （2010），使用SELENE（Kaguya）多波段成像仪数据推导月球表面的绝对反射率，太空科学。 修订版154、57-77
11。 美国宇航局（NASA）的朱迪思·H·阿尔顿（Judith H.
12 英国广播公司 尼尔·阿姆斯特朗（Neil Armstrong）与帕特里克·摩尔（Patrick Moore）对话（1970）