我们把线性回归方程变成矩阵形式

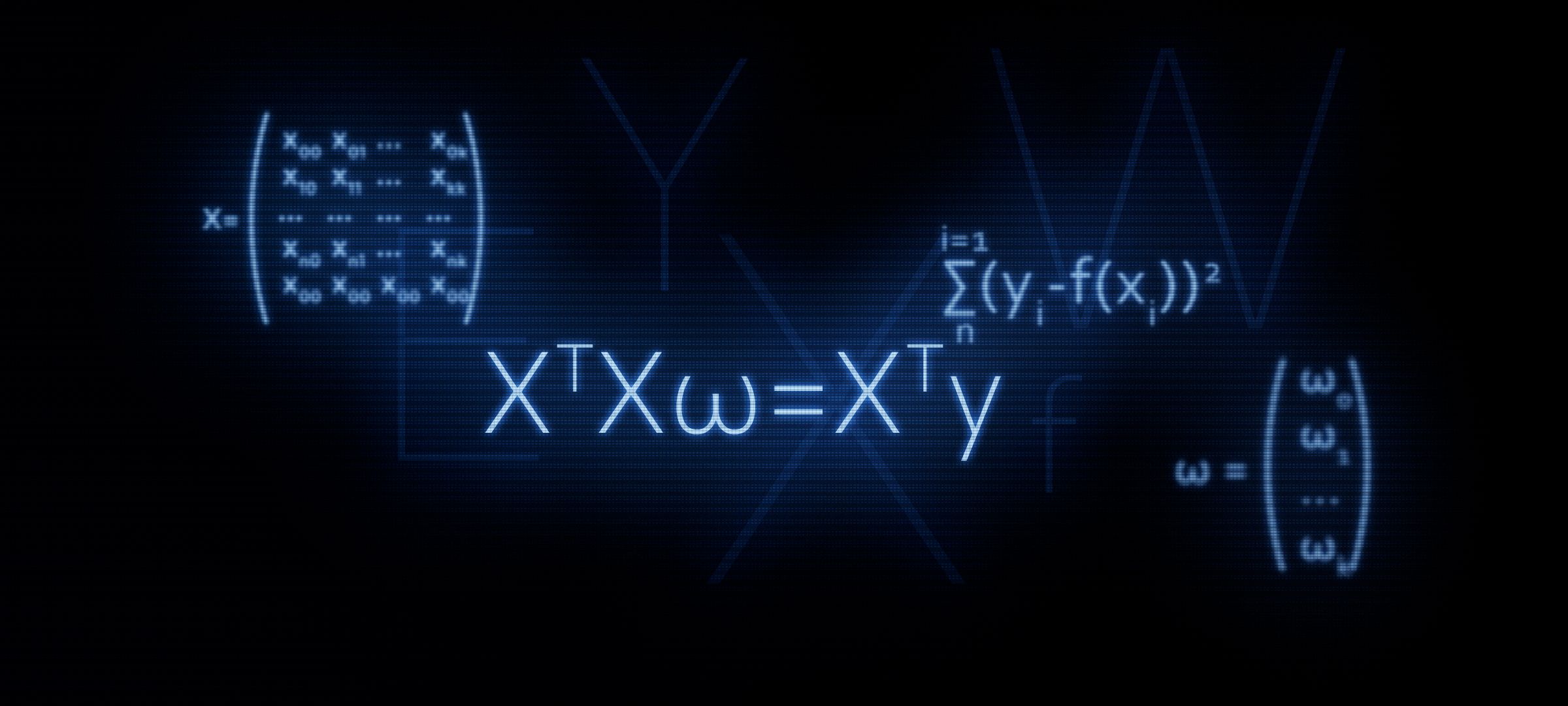
本文的目的是为新手数据专家提供支持。 在上一篇文章中，我们用手指研究了三种用于求解线性回归方程的方法：解析解，梯度下降，随机梯度下降。 然后，对于解析解，我们应用公式 $$$X ^ T X \ vec {w} = X ^ T \ vec {y}$ 。 在本文中，如标题所示，我们将证明使用此公式是合理的，换句话说，我们将独立派生该公式。

为什么需要更多地注意公式才有意义 $$$X ^ T X \ vec {w} = X ^ T \ vec {y}$ ？

在大多数情况下，是通过矩阵方程式开始进行线性回归。 同时，很少有关于公式如何得出的详细计算。

例如，在Yandex机器学习课程中，当向学生介绍正则化时，他们建议使用sklearn库中的函数，而未提及有关算法矩阵表示的任何内容。 此时某些听众可能希望更详细地了解此问题-在不使用现成函数的情况下编写代码。 为此，我们必须首先用矩阵形式的正则化器表示方程。 本文将允许那些希望掌握这种技能的人使用。 让我们开始吧。

基准线

目标

我们有许多目标值。 例如，目标可以是资产的价格：石油，黄金，小麦，美元等。 同时，通过目标指标的多个值，我们表示观察的数量。 例如，这种观察可能是该年的每月油价，也就是说，我们将有12个目标值。 我们开始介绍该符号。 我们将每个目标值指定为 $$$y_i$ 。 我们共有 $$$n$ 观察，这意味着我们可以想象我们的观察为 $$$y_1，y_2，y_3 ... y_n$ 。

回归器

我们假设存在某种程度上可以解释目标指标值的因素。 例如，美元/卢布对的汇率受油价，美联储汇率等的强烈影响。这些因素称为回归系数。 同时，目标指标的每个值都必须与回归指标的值相对应，也就是说，如果我们在2018年的每个月有12个指标，那么同一时期我们也必须有12个回归指标。 表示每个回归变量的值 $$$x_i：x_1，x_2，x_3 ... x_n$ 。 就我们而言 $$$k$ 回归器（即 $$$k$ 影响目标价值的因素）。 因此我们的回归变量可以表示为：对于第一个回归变量（例如，石油价格）： $$$x_ {11}，x_ {12}，x_ {13} ... x_ {1n}$ ，对于第二个回归指标（例如，美联储汇率）： $$$x_ {21}，x_ {22}，x_ {23} ... x_ {2n}$ 为 $$$k$ “回归者： $$$x_ {k1}，x_ {k2}，x_ {k3} ... x_ {kn}$

目标对回归变量的依赖性

假设目标依赖 $$$y_i$ 来自回归者” $$$我$ 可以通过以下形式的线性回归方程来表示“第四个”观测值：

$$

$$f（w，x_i）= w_0 + w_1 x_ {1i} + ... + w_k x_ {ki}$$

在哪里 $$$x_i$ -“ $$$我$ th的回归值从1到 $$$n$ ，

$$$k$ -回归数从1到 $$$k$

$$$w$ -角度系数，表示回归变量发生变化时，计算出的目标指标平均发生变化的量。

换句话说，我们适合所有人（除了 $$$w_0$ ），我们确定“我们的”系数 $$$w$ ，然后将系数乘以回归器的值” $$$我$ -“观察，结果我们得到了一定的近似值” $$$我$ “目标”。

因此，我们需要选择这样的系数 $$$w$ 为此，我们的近似函数的值 $$$f（w，x_i）$ 将位于尽可能接近目标值的位置。

估计近似函数的质量

我们将通过最小二乘法确定近似函数的质量估计。 在这种情况下，质量评估功能将采用以下形式：

$$

$$Err = \ sum \ limits_ {i = 1} ^ n（y_i-f（x_i））^ 2 \ rightarrow min$$

我们需要选择系数$ w $的此类值 $$$错误$ 将是最小的。

我们将方程式转换成矩阵形式

矢量视图

首先，为了使您的生活更轻松，您应注意线性回归方程式，并注意第一个系数 $$$w_0$ 没有与任何回归器相乘。 此外，当我们将数据转换为矩阵形式时，上述情况将使计算复杂化。 在这方面，建议为第一系数引入另一个回归器。 $$$w_0$ 等于一 或更确切地说，每个“ $$$我$ 该回归变量的“值”等于1-因为当乘以1时，计算结果将保持不变，并且从矩阵乘积的规则的角度来看，我们的痛苦将大大减少。

现在，为了简化材料，假设我们只有一个“ $$$我$ “观察。然后，想象回归器的值” $$$我$ 作为矢量的观察 $$$\ vec {x_i}$ 。 向量 $$$\ vec {x_i}$ 有尺寸 $$$（k \乘以1）$ 那就是 $$$k$ 行和1列：

$$

$$\ vec {x_i} = \开始{pmatrix} x_ {0i} \\ x_ {1i} \\ ... \\ x_ {ki} \ end {pmatrix} \ qquad$$

所需系数可以表示为向量 $$$\ vec {w}$ 有尺寸 $$$（k \乘以1）$ ：

$$

$$\ vec {w} = \开始{pmatrix} w_0 \\ w_1 \\ ... \\ w_k \结束{pmatrix} \ qquad$$

“的线性回归方程 $$$我$ -th“观察将采取以下形式：

$$

$$f（w，x_i）= \ vec {x_i} ^ T \ vec {w}$$

线性模型的质量评估函数将采用以下形式：

$$

$$Err = \ sum \ limits_ {i = 1} ^ n（y_i- \ vec {x_i} ^ T \ vec {w}）^ 2 \ rightarrow min$$

请注意，根据矩阵乘法的规则，我们需要对向量进行转置 $$$\ vec {x_i}$ 。

矩阵表示

向量相乘的结果是： $$$（1 \乘以k）\ centerdot（k \乘以1）= 1 \乘以1$ 如预期的那样。 该数字是近似值“ $$$我$ -th“ target。但是我们不需要估计目标的一个值，而是全部。为此，我们编写所有内容” $$$我$ 矩阵回归 $$$X$ 。 所得矩阵的维数 $$$（n \乘k）$ ：

$$$$ display $$ X = \开始{pmatrix} x_ {00}＆x_ {01}＆...＆x_ {0k} \\ x_ {10}＆x_ {11}＆...＆x_ {1k} \\ ...＆...＆...＆... \\ x_ {n0}＆x_ {n1}＆...＆x_ {nk} \ end {pmatrix} \ qquad $$显示$$

现在，线性回归方程将采用以下形式：

$$

$$f（w，X）= X \ vec {w}$$

表示目标指标的值（全部 $$$y_i$ ）每个向量 $$$\ vec {y}$ 尺寸 $$$（n \乘以1）$ ：

$$

$$\ vec {y} = \开始{pmatrix} y_ {0} \\ y_ {1} \\ ... \\ y_ {n} \ end {pmatrix} \ qquad$$

现在，我们可以以矩阵格式编写方程式，以评估线性模型的质量：

$$

$$Err =（X \ vec {w}-\ vec {y}）^ 2 \ rightarrow min$$

实际上，从这个公式我们可以进一步获得我们已知的公式 $$$X ^ T X w = X ^ T y$

怎么做？ 方括号被打开，进行了区分，结果表达式被转换等，这就是我们现在要做的。

矩阵转换

展开括号

$$$（X \ vec {w}-\ vec {y}）^ 2 =（X \ vec {w}-\ vec {y}）^ T（X \ vec {w}-\ vec {y}）$

$$$=（X \ vec {w}）^ TX \ vec {w}-\ vec {y} ^ TX \ vec {w}-（X \ vec {w}）^ T \ vec {y} + \ vec { y} ^ T \ vec {y}$

准备微分方程

为此，我们进行了一些转换。 在随后的计算中，如果向量 $$$\ vec {w} ^ T$ 将在等式中每项工作的开头进行介绍。

转换1

$$$\ vec {y} ^ TX \ vec {w} =（X \ vec {w}）^ T \ vec {y} = \ vec {w} ^ TX ^ T \ vec {y}$

这是怎么发生的？ 要回答这个问题，只需查看相乘矩阵的大小，然后在输出处看到一个数字即可 $$$const$ 。

我们编写矩阵表达式的维数。

$$$\ vec {y} ^ TX \ vec {w}：（1 \倍n）\ centerdot（n \倍k）\ centerdot（k \倍1）=（1 \倍1）= const$

$$$（X \ vec {w}）^ T \ vec {y}：（（n \乘以k）\ centerdot（k乘以1））^ T \ centerdot（n乘以1）=（1 \乘以n） \ centerdot（n \乘以1）=（1 \乘以1）= const$

$$$\ vec {w} ^ TX ^ T \ vec {y}：（1 \乘k）\ centerdot（k \乘n）\ centerdot（n \乘1）=（1 \乘1）= const$

转换2

$$$（X \ vec {w}）^ TX \ vec {w} = \ vec {w} ^ TX ^ TX \ vec {w}$

我们写类似于转换1

$$$（X \ vec {w}）^ TX \ vec {w}：（（（n \次k）\ centerdot（k \次1）））^ T \ centerdot（n \次k）\ centerdot（k \次1 ）=（1 \乘以1）= const$

$$$\ vec {w} ^ TX ^ TX \ vec {w}：（1 \乘k）\ centerdot（k \乘n）\ centerdot（n \乘k）\ centerdot（k \乘1）=（1 \乘以1）= const$

在输出中，我们得到一个必须微分的方程：
$$$Err = \ vec {w} ^ TX ^ TX \ vec {w}-2 \ vec {w} ^ TX ^ T \ vec {y} + \ vec {y} ^ T \ vec {y}$

我们区分评估模型质量的功能

通过矢量区分 $$$\ vec {w}$ ：

$$

$$\ frac {d（\ vec {w} ^ TX ^ TX \ vec {w}-2 \ vec {w} ^ TX ^ T \ vec {y} + \ vec {y} ^ T \ vec {y}） } {d \ vec {w}}$$

$$$（\ vec {w} ^ TX ^ TX \ vec {w}）'-（2 \ vec {w} ^ TX ^ T \ vec {y}）'+（\ vec {y} ^ T \ vec {y }）'= 0$

$$$2X ^ TX \ vec {w}-2X ^ T \ vec {y} + 0 = 0$

$$$X ^ TX \ vec {w} = X ^ T \ vec {y}$

问题原因 $$$（\ vec {y} ^ T \ vec {y}）'= 0$ 应该不应该，但是我们将更详细地分析确定另外两个表达式中的导数的操作。

差异1

我们揭示了区别： $$$\ frac {d（\ vec {w} ^ TX ^ TX \ vec {w}）} {d \ vec {w}} = 2X ^ TX \ vec {w}$

为了确定矩阵或向量的导数，您需要查看它们的内部。 我们看：

$$$ inline $ \ vec {w} ^ T = \开始{pmatrix} w_0＆w_1＆...＆w_k \ end {pmatrix} \ qquad $ inline $

$$$\ vec {w} = \开头{pmatrix} w_0 \\ w_1 \\ ... \\ w_k \结束{pmatrix} \ qquad$

$$$ inline $ X ^ T = \开始{pmatrix} x_ {00}＆x_ {10}＆...＆x_ {n0} \\ x_ {01}＆x_ {11}＆...＆x_ {n1} \\ ...＆...＆...＆... \\ x_ {0k}＆x_ {1k}＆...＆x_ {nk} \ end {pmatrix} \ qquad $ inline $$$ $ inline $ X = \开始{pmatrix} x_ {00}＆x_ {01}＆...＆x_ {0k} \\ x_ {10}＆x_ {11}＆...＆x_ {1k} \\ ...＆...＆...＆... \\ x_ {n0}＆x_ {n1}＆...＆x_ {nk} \ end {pmatrix} \ qquad $ inline $

表示矩阵的乘积 $$$X ^ TX$ 通过矩阵 $$。 矩阵 $$此外，它是对称的。 这些属性对我们进一步有用，请记住它们。 矩阵 $$有尺寸 $$$（k \乘以k）$ ：

$$$ inline $ A = \开始{pmatrix} a_ {00}＆a_ {01}＆...＆a_ {0k} \\ a_ {10}＆a_ {11}＆...＆a_ {1k} \\ ...＆...＆...＆... \\ a_ {k0}＆a_ {k1}＆...＆a_ {kk} \结束{pmatrix} \ qquad $ inline $

现在，我们的任务是将向量正确乘以矩阵，而不是得到“两次二乘五”，因此我们将集中精力并格外小心。

$$$ inline $ \ vec {w} ^ TA \ vec {w} = \开始{pmatrix} w_0＆w_1＆...＆w_k \ end {pmatrix} \ qquad \ times \ begin {pmatrix} a_ {00}＆a_ {01}＆...＆a_ {0k} \\ a_ {10}＆a_ {11}＆...＆a_ {1k} \\ ...＆...＆...＆... \ \ a_ {k0}＆a_ {k1}＆...＆a_ {kk} \结束{pmatrix} \ qquad \ times \开始{pmatrix} w_0 \\ w_1 \\ ... \\ w_k \结束{pmatrix} \ qquad = $内联$

$$$ inline $ = \开始{pmatrix} w_0a_ {00} + w_1a_ {10} + ... + w_ka_ {k0}＆...＆w_0a_ {0k} + w_1a_ {1k} + ... + w_ka_ {kk} \ \结束{pmatrix} \次\开始{pmatrix} w_0 \\ w_1 \\ ... \\ w_k \结束{pmatrix} \ qquad = $ inline $

$$$= \开始{pmatrix}（w_0a_ {00} + w_1a_ {10} + ... + w_ka_ {k0}）w_0 \ mkern 10mu + \ mkern 10mu ... \ mkern 10mu + \ mkern 10mu（w_0a_ {0k} + w_1a_ {1k} + ... + w_ka_ {kk}）w_k \ end {pmatrix} =$

$$$= w_0 ^ 2a_ {00} + w_1a_ {10} w_0 + w_ka_ {k0} w_0 \ mkern 10mu + \ mkern 10mu ... \ mkern 10mu + \ mkern 10mu w_0a_ {0k} w_k + w_1a_ {1k} w_k + .. 。+ w_k ^ 2a_ {kk}$

但是，我们得到了复杂的表达！ 实际上，我们得到了一个数字-标量。 而现在，我们已经做到了真正的差异化。 必须为每个系数找到获得的表达式的导数 $$$w_0 w_1 ... w_k$ 并在输出处获取尺寸向量 $$$（k \乘以1）$ 。 以防万一，我将描述操作步骤：

1）区分 $$$w_o$ 我们得到： $$$2w_0a_ {00} + w_1a_ {10} + w_2a_ {20} + ... + w_ka_ {k0} + a_ {01} w_1 + a_ {02} w_2 + ... + a_ {0k} w_ {k}$

2）区分 $$$w_1$ 我们得到： $$$w_0a_ {01} + 2w_1a_ {11} + w_2a_ {21} + ... + w_ka_ {k1} + a_ {10} w_0 + a_ {12} w_2 + ... + a_ {1k} w_ {k}$

3）区分 $$$w_k$ 我们得到： $$$w_0a_ {0k} + w_1a_ {1k} + w_2a_ {2k} + ... + w _ {{k-1）} a _ {{k-1）k} + a_ {k0} w_0 + a_ {k1} w_1 + a_ {k2} w_2 + ... + 2w_ka_ {kk}$

在输出中，承诺的大小向量 $$$（k \乘以1）$ ：

$$

$$\开始{pmatrix} 2w_0a_ {00} + w_1a_ {10} + w_2a_ {20} + ... + w_ka_ {k0} + a_ {01} w_1 + a_ {02} w_2 + ... + a_ {0k} w_ {k} \\ w_0a_ {01} + 2w_1a_ {11} + w_2a_ {21} + ... + w_ka_ {k1} + a_ {10} w_0 + a_ {12} w_2 + ... + a_ {1k} w_ { k} \\ ... \\ ... \\ ... \\ w_0a_ {0k} + w_1a_ {1k} + w_2a_ {2k} + ... + w _ {（k-1）} a _ {（k -1）k} + a_ {k0} w_0 + a_ {k1} w_1 + a_ {k2} w_2 + ... + 2w_ka_ {kk} \ end {pmatrix}$$

如果仔细看一下向量，您会注意到向量的左元素和右元素可以按照这样的方式进行分组，从而可以将向量与显示的向量区分开 $$$\ vec {w}$ 大小 $$$（k \乘以1）$ 。 举个例子 $$$w_1a_ {10}$ （向量顶行的左元素） $$$+ a_ {01} w_1$ （向量顶行的右元素）可以表示为 $$$w_1（a_ {10} + a_ {01}）$ 和 $$$w_2a_ {20} + a_ {02} w_2$ -怎么 $$$w_2（a_ {20} + a_ {02}）$ 等 在每一行上。 组别：

$$

$$\开始{pmatrix} 2w_0a_ {00} + w_1（a_ {10} + a_ {01}）+ w_2（a_ {20} + a_ {02}）+ ... + w_k（a_ {k0} + a_ { 0k}）\\ w_0（a_ {01} + a_ {10}）+ 2w_1a_ {11} + w_2（a_ {21} + a_ {12}）+ ... + w_k（a_ {k1} + a_ {1k }）\\ ... \\ ... \\ ... \\ w_0（a_ {0k} + a_ {k0}）+ w_1（a_ {1k} + a_ {k1}）+ w_2（a_ {2k } + a_ {k2}）+ ... + 2w_ka_ {kk} \结尾{pmatrix}$$

取出向量 $$$\ vec {w}$ 在输出中，我们得到：

$$$$显示$$ \开始{pmatrix} 2a_ {00}＆a_ {10} + a_ {01}＆a_ {20} + a_ {02}＆...＆a_ {k0} + a_ {0k} \\ a_ {01} + a_ {10}＆2a_ {11}＆a_ {21} + a_ {12}＆...＆a_ {k1} + a_ {1k} \\ ...＆...＆.. 。＆...＆... \\ ...＆...＆...＆...＆... \\ ...＆...＆...＆...＆.. 。\\ a_ {0k} + a_ {k0}＆a_ {1k} + a_ {k1}＆a_ {2k} + a_ {k2}＆...＆2a_ {kk} \结束{pmatrix} \次\开始{pmatrix} w_0 \\ w_1 \\ ... \\ ... \\ ... \\ w_k \ end {pmatrix} \ qquad $$ display $$

现在，让我们看一下结果矩阵。 矩阵是两个矩阵的和 $$$A + A ^ T$ ：

$$$$显示$$ \开始{pmatrix} a_ {00}＆a_ {01}＆a_ {02}＆...＆a_ {0k} \\ a_ {10}＆a_ {11}＆a_ {12}＆ ...＆a_ {1k} \\ ...＆...＆...＆...＆... \\ a_ {k0}＆a_ {k1}＆a_ {k2}＆...＆ a_ {kk} \结束{pmatrix} + \开始{pmatrix} a_ {00}＆a_ {10}＆a_ {20}＆...＆a_ {k0} \\ a_ {01}＆a_ {11}＆ a_ {21}＆...＆a_ {k1} \\ ...＆...＆...＆...＆... \\ a_ {0k}＆a_ {1k}＆a_ {2k} ＆...＆a_ {kk} \结束{pmatrix} \ qquad $$显示$$

回想一下，我们注意到矩阵的一个重要属性 $$-是对称的。 基于此属性，我们可以放心地说 $$$A + A ^ T$ 等于 $$$2A$ 。 通过显示逐元素乘积可以很容易地验证 $$$X ^ TX$ 。 我们不会在这里这样做，希望的人可以自己进行验证。

让我们回到我们的表情。 进行转换后，结果如我们所愿：

$$

$$（A + A ^ T）\次\开始{pmatrix} w_0 \\ w_1 \\ ... \\ w_k \ end {pmatrix} \ qquad = 2A \ vec {w} = 2X ^ TX \ vec {w}$$

因此，我们应对了第一次分化。 我们转到第二个表达式。

差异化2

$$$\ frac {d（2 \ vec {w} ^ TX ^ T \ vec {y}）} {d \ vec {w}} = 2X ^ T \ vec {y}$

让我们沿着人迹罕至的道路走吧。 它会比上一个短很多，所以不要离屏幕太远。

我们揭示了按元素的向量和矩阵：

$$$ inline $ \ vec {w} ^ T = \开始{pmatrix} w_0＆w_1＆...＆w_k \ end {pmatrix} \ qquad $ inline $

$$$ inline $ X ^ T = \开始{pmatrix} x_ {00}＆x_ {10}＆...＆x_ {n0} \\ x_ {01}＆x_ {11}＆...＆x_ {n1} \\ ...＆...＆...＆... \\ x_ {0k}＆x_ {1k}＆...＆x_ {nk} \ end {pmatrix} \ qquad $ inline $

$$$\ vec {y} = \开始{pmatrix} y_0 \\ y_1 \\ ... \\ y_n \ end {pmatrix} \ qquad$

有一阵子，我们从演算中删除演绎器-它发挥的作用不大，然后我们将其放回原处。 将向量乘以矩阵。 首先，我们将矩阵相乘 $$$X ^ T$ 在向量上 $$$\ vec {y}$ ，这里我们没有任何限制。 获取大小向量 $$$（k \乘以1）$ ：

$$

$$\开始{pmatrix} x_ {00} y_0 + x_ {10} y_1 + ... + x_ {n0} y_n \\ x_ {01} y_0 + x_ {11} y_1 + ... + x_ {n1} y_n \\ ... \\ x_ {0k} y_0 + x_ {1k} y_1 + ... + x_ {nk} y_n \ end {pmatrix} \ qquad$$

执行以下操作-将向量相乘 $$$\ vec {w}$ 到所得向量。 在输出中，一个数字将等待我们：

$$

$$\开始{pmatrix} w_0（x_ {00} y_0 + x_ {10} y_1 + ... + x_ {n0} y_n）+ w_1（x_ {01} y_0 + x_ {11} y_1 + ... + x_ {n1 } y_n）\ mkern 10mu + \ mkern 10mu ... \ mkern 10mu + \ mkern 10mu w_k（x_ {0k} y_0 + x_ {1k} y_1 + ... + x_ {nk} y_n）\ end {pmatrix} \ qquad$$

然后，我们对其进行区分。 在输出中，我们得到一个尺寸向量 $$$（k \乘以1）$ ：

$$

$$\开始{pmatrix} x_ {00} y_0 + x_ {10} y_1 + ... + x_ {n0} y_n \\ x_ {01} y_0 + x_ {11} y_1 + ... + x_ {n1} y_n \\ ... \\ x_ {0k} y_0 + x_ {1k} y_1 + ... + x_ {nk} y_n \ end {pmatrix} \ qquad$$

它像什么吗？ 好吧！ 这是矩阵的乘积。 $$$X ^ T$ 在向量上 $$$\ vec {y}$ 。

这样，第二次区分成功完成。

而不是结论

现在我们知道平等是如何产生的。 $$$X ^ T X \ vec {w} = X ^ T \ vec {y}$ 。

最后，我们描述了一种转换主要公式的快速方法。

根据最小二乘法估算模型的质量：
$$$\ sum \ limits_ {i = 1} ^ n（y_i-f（x_i））^ 2 \ mkern 20mu = \ mkern 20mu \ sum \ limits_ {i = 1} ^ n（y_i- \ vec {x_i} ^ T \ vec {w}）^ 2 =$

$$$=（X \ vec {w}-\ vec {y}）^ 2 \ mkern 20mu = \ mkern 20mu（X \ vec {w}-\ vec {y}）^ T（X \ vec {w}-\ vec {y}）\ mkern 20mu = \ mkern 20mu \ vec {w} ^ TX ^ TX \ vec {w}-2 \ vec {w} ^ TX ^ T \ vec {y} + \ vec {y} ^ T \ vec {y}$

我们区分结果表达式：
$$$\ frac {d（\ vec {w} ^ TX ^ TX \ vec {w}-2 \ vec {w} ^ TX ^ T \ vec {y} + \ vec {y} ^ T \ vec {y}） } {d \ vec {w}} =$$$$2X ^ TX \ vec {w}-2X ^ T \ vec {y} = 0$

$$$X ^ TX \ vec {w} = X ^ T \ vec {y}$

$$$\ leftarrow$ 作者的先前工作-“我们解决了简单线性回归方程”
$$$\ rightarrow$ 作者的下一个作品-“咀嚼逻辑回归”

文学作品

互联网资源：

1） habr.com/en/post/278513
2） habr.com/ru/company/ods/blog/322076
3） habr.com/en/post/307004
4） nabatchikov.com/blog/view/matrix_der

教科书，任务集：

1）关于高等数学的讲义：完整课程/ D.T. 书面-第四版。 -M.：Iris Press，2006年
2）应用回归分析/ N. Draper，G。Smith-第2版。 -M .：《金融与统计》，1986年（英语）
3）解决矩阵方程的任务：
function-x.ru/matrix_equations.html
mathprofi.ru/deistviya_s_matricami.html