即使是远离物理学的人,也知道任何信号的最大可能数据速率等于真空中的光速。 用字母“ c”表示,每秒几乎30万公里。 真空中的光速是基本的物理常数之一。 爱因斯坦的狭义相对论(SRT)得出的结论是,不可能在三维空间中达到超过光速的速度。
通常,当声称STO禁止信息以高于光速的速度进行传输时,会隐含一个假设,即“将信息附加到光子并进行传输”不再是其他方式。 但是,还有另一种方法并不矛盾,而是“规避”了禁止SRT的方法。 众所周知的物理假设-全息原理(今天广泛使用的理论物理学工具)表明了一个有趣的事实:“可以将发生在三维空间中的现象投影到遥远的“屏幕上,而不会丢失信息”-伦纳德·苏斯金德
“不丢失信息”是指,如果我们了解到我们的信息宇宙实际上仅存在于具有单个时间坐标的全息地平线(屏幕)的2D表面上,并且物理学的基本定律是自然的,则不需要进行投机投影操作。有损失的信息编码方式。 然后得出结论:如果我们知道宇宙的极其简单的全息代码-在屏幕上编码和移动信息的自然机制,那么可能会出现新的可能性之一-我们可以检测出无需进行传输和接收信息的机制限速灯。 将所有内容放在一起进行合成就像解决一个巨大的难题。 为了生成宇宙的全息代码,其搜索思想是利用全息图的主要属性:全息图的每个最小部分都包含有关整个对象的信息。 基于这一事实,我们为三维空间中任何点的相干振荡提供了一个非常简单的公式,并将其加载到常规计算机动态模拟器(甚至适合3D MAX之类的程序)中,并在常规计算机屏幕上,我们可以看到球形表面的两半,突起的动力学以及标准模型基本粒子的众多特性。
请注意:一个极其简单的参数公式会生成三代的投影动力学-基本粒子的整个动物园:48个费米子和12个玻色子,并且被物理学家-理论家和实验者的巨大努力所获得的实验数据所证实,几乎一百年来的理论和实践研究。 可视化科学数据的方法使您可以在常规计算机上看到不可见的物体-一个点的相干振荡的一个周期,该周期由其半径矢量标识:
在这种基本的,有前景的“全息背景”下,机电设备的出现是自然的,因为它使用了与全息图完全相同的基本特性:相干性,干涉性和转子点相干振荡的相同公式。 如果将全息宇宙的假设转化为工作理论,则只有在实验中以及在其实际应用中更好地反复证实其预测的情况下,全息全息的假设才能转化为工作理论。 随着实验基础的出现-物理金字塔的顶部,实际上是该理论一部分的假设被暂时从批评中删除,直到实验的实际实施和进行测量。
一个不寻常的陀螺仪的设计看起来像这样:一个带有磁体的球形转子悬浮在带有电磁体的定子的抽空球形腔内。 在计算机系统的控制下,转子可以被迫在64个方向中的任意一个方向上绕质心的一个固定点旋转,并且每个周期同时绕三个轴旋转。
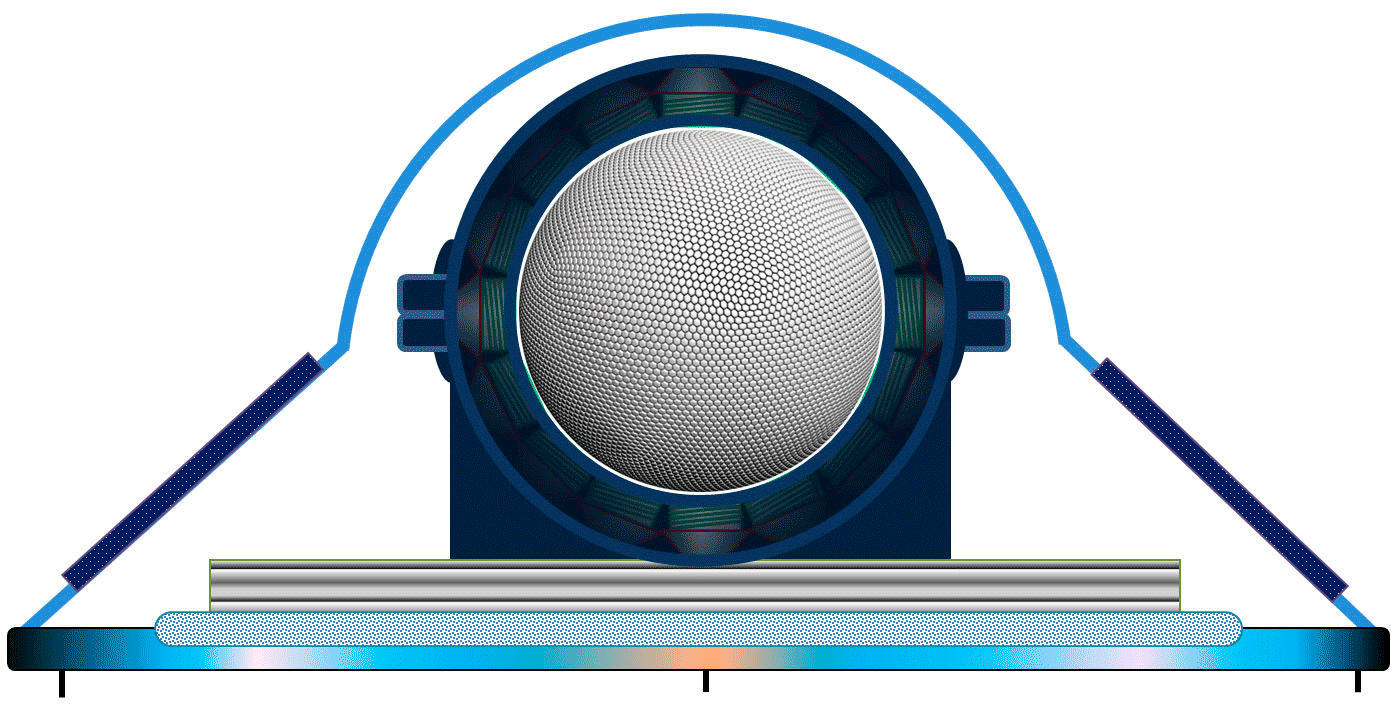
如果在普通的静止陀螺仪中,转子在一个周期内绕一个轴旋转一圈,那么在不寻常的陀螺仪中,处于真空中的球形转子在与加速观测器相关的笛卡尔坐标的三个固定轴上绕一圈。 转子质量元素(使用此旋转算法)产生相干振荡,并且加速度与半轴的方向相关。 加速度的结和波腹形成六个相同且沿直径方向的组的静止干涉图样。

我们有六组旋转加速度,根据全息原理,它们由熵的梯度表示。 更准确地说,我们谈论的是根据熵衡量的信息量,进而,可以将定向的加速度(熵梯度)组投影到球形2D屏幕的六个相对侧上,而固定温度梯度为背景而不会造成损失信息。 在观察者不可见的情况下,我们通常以六个白色圆圈在普朗克空间天文台的照片中显示熵梯度。 使用计算机系统控制转子的运动,我们可以改变方向并成对移动投影(六个中的四个),但是现在它们由信息本身(熵梯度)表示,它在屏幕上相对于具有单个时间坐标的固定温度梯度的背景。
随着物质的运动,这种熵的变化导致熵力的出现。 由于根据全息原理的守恒定律,屏幕上不会丢失任何一点,因此有可能在传输信息的同时接收信息,因此测量熵力就足够了,相对于固定定子,将其应用于转子的质心。 熵力是球形全息屏幕的静止温度梯度与定向加速度(物质加速度的一阶导数)引起的运动熵梯度相互作用的结果。
Fentr =ΔTΔS;
其中Fentr-熵力ΔT-屏幕上的温度梯度, ΔS-熵梯度与质量元素的受控加速度相关。
如果预期的未补偿熵在封闭系统中表现出来(理论上不考虑物质的相干状态应与动量守恒定律相抵触),则全息理论是有效的,并且所有的观测者,接收者和发射者都是信息位于具有单个时间坐标的屏幕的同一表面上,并且可以在它们之间实现交换信息。 以上意味着我们需要考虑不寻常的陀螺仪的立即实际实施。 一个不寻常的陀螺仪作为实验装置将能够回答以下问题:“全息原理证明了我们的“ 3D +1”维时空的物理原理等同于超维表面上具有2D +1维的物理原理。 ? 换句话说,我们可以对全息假说进行“划分”。
现在简要介绍一下内容-我们回答“为什么信息传输取决于一致性?”这个问题,我们使用独特且极其简单的公式研究计算机建模。 如果从屏幕上接收信息对我们来说很重要,我们可以先阅读最重要的信息-屏幕上的全局温度梯度。 描述我们收到的信息的一种方法是使用热力学。 加速度和温度密切相关。 刚体的质量要素在相干振荡期间的加速度在周期中的空间中是不动的,并且沿直径方向定向,因此在球形转子中,我们有六个相等的组。 根据全息原理,我们进行了投机操作,将它们投影到屏幕上(不丢失信息)。 另外,我们可以通过加速度来表示熵的增量。 由于可以从屏幕上的热力学推导牛顿第二定律(根据Verlinde的步骤),因此这意味着在六个加速度投影中的四个成对移动时,会产生一个定向的熵力,这是我们在背景下猛加的结果温度梯度的总和,指的是转子的质心。 测得的熵力-有关全局温度梯度的信息,无需限制光的距离和速度即可读取。 不能用根本不同的方式来完成此操作,因为该物质的其余部分处于去相干状态(没有相干性),并且屏幕上的信息均匀模糊,并且不集中在某个区域。 尽管采取了即时措施,但由于违反了过去的信息无法在屏幕上更改,因此没有违反因果关系原则。 不违反信息保存法。 因此,我们有一个真正的设备,可以以相干振荡的频率(例如166 Hz)获得信息,而不受任何扫描方向的光的距离和速度的限制。 异常陀螺仪转子的相干振荡使您可以直接从全息屏幕接收信息。
总而言之,我们可以假定费米悖论的解决方案是,如果我们的全息宇宙中存在智能文明,那么它们将不会使用电磁方法相互交换信息。 无需在此特定搜索方向上进行投资。 我们假设使用全息屏幕作为交流渠道,使他们可以交换信息而不受光的距离和速度的限制。