C＃中的不安全通用数学

不幸的是，要把我刚开始的丑陋的名字适当地翻译成俄语并不容易。 令我惊讶的是，官方MSDN文档将其称为“泛型”“模板”（我想类似于C++模板）。 在引起我注意的第4版"CLR通过C# "CLR ”中， 彼得翻译的杰弗里·里希特 （ Jeffrey Richter ）将泛型称为“泛化”，它更好地反映了这一概念。 本文将讨论C#不安全的广义数学运算 。 考虑到C#并非旨在用于高性能计算（尽管当然可以，但它不能与相同的C/C++竞争），因此BCL数学运算并未引起太多关注。 让我们尝试使用C#和CLR简化基本算术类型的工作。

问题陈述

免责声明 ：本文将包含许多代码片段，其中一些我将通过与Andrey Shchekin的精彩资源SharpLab （ Gi r tHub ）的链接进行说明。

大多数计算以一种或另一种方式归结为基本操作。 加法，减法（求反，求反），乘法和除法可以通过比较和检查相等性的操作来补充。 当然，所有这些动作都可以轻松，简单地在C#的任何基本算术类型的变量上执行。 唯一的问题是C#应该在编译时就知道对特定类型执行了操作，而且似乎不可能写出一种有效地（透明地）相加两个整数和两个浮点数的方法。

让我们指定对执行一些简单数学运算的假设通用方法的期望：

1. 方法必须具有通用的类型限制，以防止我们尝试添加（或乘，除）两个任意类型。 我们需要一些通用类型约束。
2. 为了保证实验的纯度，接受和返回的类型必须相同。 例如，二进制运算符必须具有(T, T) => T形式的签名(T, T) => T
3. 该方法应至少部分优化。 例如，无处不在的拳击是不可接受的。

那邻居呢？

让我们看一下F# 。 我不擅长F# ，但是大多数C#限制是由CLR限制决定的，这意味着F#会遇到相同的问题。 您可以尝试声明一个显式的广义加法和通常的加法，并查看F#类型推断系统的含义：

 let add_gen (x : 'a) (y : 'a) = x + y let add xy = x + y add_gen 5.0 6.0 |> ignore add 5.0 6.0 |> ignore 

在这种情况下，两种方法都将变成非通用的，并且生成的代码将是相同的。 给定F#类型系统的刚性，其中不存在int -> double形式的隐式转换，在首次使用double类型的参数（用C#术语）调用这些方法之后，使用其他类型的参数调用方法（即使由于类型转换而可能导致精度损失）更多会失败。

值得注意的是，如果用相等运算符=替换+运算符， 图片会略有不同 ：两种方法都变成了通用的（从C#的角度来看），并且调用了F#可用的特殊辅助方法来执行比较。

 let eq_gen (x : 'a) (y : 'a) = x = y let eq xy = x = y eq_gen 5.0 6.0 |> ignore eq_gen 5 6 |> ignore eq 5.0 6.0 |> ignore eq 5 6 |> ignore 

Java呢？

我很难谈论Java ，但是据我所知，重要类型不是我们惯用的形式，但仍然有原始类型。 为了在Java使用基元Java有一些包装器 （例如，基元按值long的引用Long ），它们具有一个通用的基类Number 。 因此，您可以使用Number来部分概括操作，但这是一种引用类型，不太可能对性能产生积极影响。

如果我错了，请纠正我。

C++ ？

C++是作弊者的一种语言。
C++为某些人认为... 不自然的功能铺平了道路。
从广义上讲， 模板 （aka模板）与概括（泛型）相反，是template 。 声明模板时，可以显式限制此模板可用的类型。 因此，例如在C++ ，以下代码有效：

 #include <iostream> template<typename T, std::enable_if_t<std::is_arithmetic<T>::value>* = nullptr> T Add (T left, T right) { return left + right; } int main() { std::cout << Add(5, 6) << std::endl; std::cout << Add(5.0, 6.0) << std::endl; // std::cout << Add("a", "b") << std::endl; Does not compile } 

不幸的是， is_arithmetic允许使用char和bool作为参数。 另一方面，尽管整数类型的实际大小取决于平台/编译器/月相，但是char在C#术语中可以等同于sbyte 。

动态打字语言

最后，考虑几种动态类型化（和解释性 ）的语言，这些语言通过计算得到了增强。 在这种语言中，计算的一般化通常不会引起问题：如果参数类型适合于有条件地执行加法运算，则将执行该操作，否则将失败并显示错误。

在Python （3.7.3 x64）中：

 def add (x, y): return x + y type(add(5, 6)) # <class 'int'> type(add(5.0, 6.0)) # <class 'float'> type(add('a', 'b') # <class 'str'> 

在R （3.6.1 x64）中

 add <- function(x, y) x + y # Or typeof() vctrs::vec_ptype_show(add(5, 6)) # Prototype: double vctrs::vec_ptype_show(add(5L, 6L)) # Prototype: integer vctrs::vec_ptype_show(add("5", "6")) # Error in x + y : non-numeric argument to binary operator 

相反，在C＃世界中：我们限制数学函数的广义类型

不幸的是，我们不能这样做。 在C#基本类型是按值类型，即 尽管从System.Object （和System.ValueType ）继承的结构却没有太多共同点。 一个自然而合理的限制是where T : struct 。 从C# 7.3我们具有where T : unmanaged约束，这意味着T是非 , null 。 除了我们需要的原始算术类型之外， char ， bool ， decimal ， 任何 Enum以及所有字段都具有相同unmanaged类型的任何结构都可以满足这些要求。 即 此类型将通过测试：

 public struct Coords<T> where T : unmanaged { public TX; public TY; } 

因此，我们不能编写仅接受所需算术类型的通用函数。 因此，本文标题中的Unsafe -我们将不得不依靠程序员使用我们的代码。 如果程序员将不兼容类型的对象作为参数传递，则尝试调用假设的通用方法T Add<T>(T left, T right) where T : unmanaged将导致无法预测的结果。

第一次实验，天真： dynamic

dynamic是可以帮助我们解决问题的第一个显而易见的工具。 当然，将dynamic用于计算绝对是没有用的- dynamic等效于object ，并且带有dynamic变量的被调用方法被编译器转换为可怕的反射。 作为奖励-包装/拆装我们的按值类型。 这是一个例子 ：

 public class Class { public static void Method() { var x = Add(5, 6); var y = Add(5.0, 6.0); } private static dynamic Add(dynamic left, dynamic right) => left + right; } 

只需查看Method方法的IL ：

 .method public hidebysig static void Method () cil managed { // Method begins at RVA 0x2050 // Code size 53 (0x35) .maxstack 8 IL_0000: ldc.i4.5 IL_0001: box [System.Private.CoreLib]System.Int32 IL_0006: ldc.i4.6 IL_0007: box [System.Private.CoreLib]System.Int32 IL_000c: call object Class::Add(object, object) IL_0011: pop IL_0012: ldc.r8 5 IL_001b: box [System.Private.CoreLib]System.Double IL_0020: ldc.r8 6 IL_0029: box [System.Private.CoreLib]System.Double IL_002e: call object Class::Add(object, object) IL_0033: pop IL_0034: ret } // end of method Class::Method 

加载5 ， 打包 ，加载6 ，打包，称为object Add(object, object) 。
选择显然不适合我们。

第二个实验，“在额头上”

好吧， dynamic不是适合我们的，但是我们类型的数量是有限的，并且它们是预先知道的。 让我们用分支撬棍武装自己并将其写下来：如果我们的类型是 ，让我们计算一下，否则-这是例外。

 public static T Add<T>(T left, T right) where T : unmanaged { if(left is int i32Left && right is int i32Right) { // ??? } // ... throw new NotSupportedException(); } 

III，这里我们遇到一个问题。 如果您了解我们正在使用的类型，则仍然可以对它们应用操作，那么需要将结果条件int转换为未知类型T ，这不是很简单。 return (T)(i32Left + i32Right)不会编译-无法保证T为int （即使我们知道它是int ）。 您可以尝试两次转换return (T)(object)(i32Left + i32Right) 。 首先，打包数量，然后在T解包T 仅当类型在包装之前和包装之后匹配时 ，此方法才起作用。 您不能打包int ，但可以将其解压缩为double ，即使存在隐式转换int -> double 。 此代码的问题是即使在if情况下，巨大的分支和大量的拆包程序也是if 。 这个选项也不好。

反射和元数据

好吧，玩就够了。 每个人都知道C#存在可以被覆盖的运算符。 那里有+ ， - ， == !=等。 我们要做的就是提取与运算符相对应的T型静态方法，例如，加法-仅此而已。 好吧，是的，还是几个包，但是没有分支，也没有问题。 可以使用T类型缓存整个对象，并且通常可以以各种方式加速该过程，从而将一种数学运算减少为调用单个反射方法。 好吧，像这样：

 public static T Add<T>(T left, T right) where T : unmanaged { // Simple example without cache. var method = typeof(T) .GetMethod(@"op_Addition", new [] {typeof(T), typeof(T)}) ?.CreateDelegate(typeof(Func<T, T, T>)) as Func<T, T, T>; return method?.Invoke(left, right) ?? throw new InvalidOperationException(); } 

不幸的是，这不起作用 。 事实是算术类型（但不是decimal ） 没有这种静态方法。 所有操作都是通过IL操作（例如add 。 正反射不能解决我们的问题。

System.Linq.Expressions

John Skeet的博客（由Marc Gravell撰写）中介绍了基于Expressions的解决方案。
这个想法很简单。 假设我们有一个支持操作+的类型T 让我们创建一个这样的表达式：

 (x, y) => x + y; 

之后，缓存后，我们将使用它。 构建这样的表达式非常容易。 我们需要两个参数和一个操作。 因此，让我们写下来。

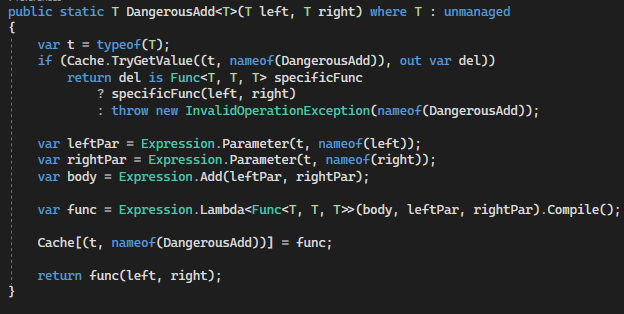
 private static readonly Dictionary<(Type Type, string Op), Delegate> Cache = new Dictionary<(Type Type, string Op), Delegate>(); public static T Add<T>(T left, T right) where T : unmanaged { var t = typeof(T); // If op is cached by type and function name, use cached version if (Cache.TryGetValue((t, nameof(Add)), out var del)) return del is Func<T, T, T> specificFunc ? specificFunc(left, right) : throw new InvalidOperationException(nameof(Add)); var leftPar = Expression.Parameter(t, nameof(left)); var rightPar = Expression.Parameter(t, nameof(right)); var body = Expression.Add(leftPar, rightPar); var func = Expression.Lambda<Func<T, T, T>>(body, leftPar, rightPar).Compile(); Cache[(t, nameof(Add))] = func; return func(left, right); } 

有关表达式树和委托的有用信息已发布在中心上

从技术上讲，表达式使我们能够解决所有问题-任何基本操作都可以简化为调用通用方法。 可以使用更复杂的表达式以相同的方式编写任何更复杂的操作。 这几乎足够了。

我们违反了所有规则

是否可以使用CLR/C#的功能实现其他目标？ 让我们看看通过不同类型的加法生成代码的年份 ：

 public class Class { public static double Add(double x, double y) => x + y; public static int Add(int x, int y) => x + y; // Decimal only to show difference public static decimal Add(decimal x, decimal y) => x + y; } 

相应的IL代码包含相同的指令集：

 ldarg.0 ldarg.1 add ret 

这是用于add算术基本类型的附加操作码。 在此位置的static decimal decimal.op_Addition(decimal, decimal)调用static decimal decimal.op_Addition(decimal, decimal) 。 但是，如果我们编写一个将被概括但完全包含此IL代码的方法怎么办？ 好吧，约翰·斯基特警告说，这不值得 。 就他而言，他考虑了所有类型（包括decimal ），以及它们的nullable为nullable类似物。 这将需要非常不平凡的IL操作，并且必然会导致错误。 但是我们仍然可以尝试执行基本操作。

令我惊讶的是， Visual Studio不包含IL项目和IL文件的模板。 您不仅可以在IL采用和描述部分代码，还可以将其包含在程序集中。 自然，开源会为我们提供帮助。 ILSupport项目包含IL项目的模板，以及可以添加到*.csproj以在项目中包含IL代码的一组指令。 当然，要在IL描述所有内容非常困难，因此该项目的作者使用了带有ForwardRef标志的内置MethodImpl属性。 此属性使您可以将方法声明为extern ，而不描述方法的主体。 看起来像这样：

 [MethodImpl(MethodImplOptions.ForwardRef)] public static extern T Add<T>(T left, T right) where T : unmanaged; 

下一步是使用IL代码在*.il文件中编写该方法的实现：

 .method public static hidebysig !!T Add<valuetype .ctor (class [mscorlib]System.ValueType modreq ([mscorlib]System.Runtime.InteropServices.UnmanagedType)) T>(!!T left, !!T right) cil managed { .param type [1] .custom instance void System.Runtime.CompilerServices.IsUnmanagedAttribute::.ctor() = (01 00 00 00 ) ldarg.0 ldarg.1 add ret } 

没有地方明确引用类型!!T ，我们建议CLR添加两个参数并返回结果。 没有类型检查，一切都取决于开发人员的良心。 出人意料的是，它可以工作并且相对较快。

有点基准

诚实的基准可能建立在一些相当复杂的表达式上，将其“正面”计算与这些危险的IL方法进行比较。 我写了一个简单的算法，将先前计算并存储在double精度数组中的数字平方求和，然后将最终数量除以数字数。 为了执行该操作，我像正常人一样使用C#运算符+ ， *和/ ，使用Expressions构建的函数以及IL函数。

 BenchmarkDotNet=v0.12.0, OS=Windows 10.0.18362 Intel Core i7-2700K CPU 3.50GHz (Sandy Bridge), 1 CPU, 8 logical and 4 physical cores .NET Core SDK=3.1.100 [Host] : .NET Core 3.1.0 (CoreCLR 4.700.19.56402, CoreFX 4.700.19.56404), X64 RyuJIT Job-POXTAH : .NET Core 3.1.0 (CoreCLR 4.700.19.56402, CoreFX 4.700.19.56404), X64 RyuJIT Runtime=.NET Core 3.1 

我们的不安全代码慢了大约2.5倍（就一次操作而言）。 这可以归因于以下事实：在“前额”计算的情况下，编译器将a + b编译为add op代码，在不安全的方法的情况下，将调用静态函数，该函数自然较慢。

而不是结论：when true != true

几天前，我从 Jared Parsons看到了这样一条推文 ：

在某些情况下，以下内容将显示“ false”
布尔b = ...
如果（b）Console.WriteLine（b.IsTrue（））;

这是该条目的答案，它显示了bool验证代码true ，看起来像这样：

 public static bool IsTrue(this bool b) { if (b == true) return true; else if (b == false) return false; else return !true && !false; } 

检查似乎多余，对不对？ Jared提出了一个反例，演示了 bool行为的一些特征 。 这个想法是bool是byte （ sizeof(bool) == 1 ），而false匹配0 ， true匹配1 。 只要您不摆动指针， bool表现就可以明确且可预测。 但是，正如Jared所示，您可以使用2作为初始值来创建bool值，并且部分检查将正确失败：

 bool b = false; byte* ptr = (byte*)&b; *ptr = 2; 

我们可以使用不安全的数学运算来达到类似的效果（这不适用于Expressions ）：

 var fakeTrue = Subtract<bool>(false, true); var val = *(byte*)&fakeTrue; if(fakeTrue) Assert.AreNotEqual(fakeTrue, true); else Assert.Fail("Clause not entered."); 

是的，是的，我们在true分支内检查条件是否为true ，并且我们期望实际上不是true 。 为什么会这样呢？ 如果不检查就从0 （ =false ） 1 （ =true ）减去，那么对于byte这将等于255 。 当然， 255 （我们的fakeTrue ）不是1 （真正的true ），因此将执行assert。 分支的工作方式不同。

if发生反转：插入条件分支； 如果条件为false ，则在if块结束之后发生到该点的转换。 验证由brfalse / brfalse_S 。 它将堆栈上的最后一个值与零进行比较。 如果值为零，则为false ，我们跳过if块。 在我们的例子中， fakeTrue不等于零，因此检查通过，并且执行继续在if块内进行，在该块中，我们将fakeBool与真实值进行比较，得到否定的结果。

UPD01：
在使用shai_hulud和blowin在评论中讨论之后，我在基准测试中添加了另一种方法来实现一个分支，例如if(typeof(T) == typeof(int)) return (T)(object)((int)(object)left + (int)(object)right); 。 尽管事实上JIT应该优化检查，至少在T是一个struct ，这种方法的运行速度仍然慢一个数量级。 优化转换T > int > T或是否使用装箱/拆箱并不明显。 基准测试的结果不受MethodImpl标志的明显影响。

UPD02：
注释中的xXxVano显示了一个按类型使用分支的示例，并使用Unsafe.As<TFrom, TTo>()将T <->转换为特定类型。 与通常的分支和通过object自定义类似，我为所有算术类型编写了三个带有分支的操作​​（加，乘和除），之后添加了另一个基准（ UnsafeBranchSum ）。 尽管事实上所有方法（表达式除外）都会生成几乎相同的asm代码（据我对汇编器的有限了解，我可以判断），但出于某种未知的原因，与直接求和（ DirectSum ）和使用泛型和IL代码。 对于这种影响，我没有任何解释，因为花费的时间与N成正比增长，这表明尽管有JIT的魔力，但每个操作都有某种恒定的开销。 方法的IL版本缺少此开销。 , IL - , / / , 100% ( , ).
, , - .