
量子计算机和量子计算是一个新的流行语 ,与人工智能 , 机器学习和其他高科技术语一起被添加到我们的信息空间中。 同时,我无法在Internet上找到会令我困惑的“量子计算机的工作原理”之谜。 是的,有很多出色的作品,包括在《哈布雷》(见《 资源清单》 )上的评论,通常会出现在评论中,这些评论甚至更具参考价值和有用性,但正如他们所说的那样,头部中的图片并没有加在一起。
最近,同事们问我:“您了解量子计算机的工作原理吗? 您能告诉我们吗?”然后我意识到,将完整图片折叠在脑海中的问题不仅是我的。
结果,人们试图将有关量子计算机的信息汇编成一个一致的逻辑方案,在该逻辑方案中,从根本上讲,无需深入研究量子世界的数学和结构 ,就可以解释量子计算机是什么,其工作原理以及面临的问题。科学家在其创建和运营中。
目录
免责声明
(到内容)
作者不是量子计算专家,本文的目标读者是同一位IT专家,而不是量子专家 ,他们也想在脑海中收集一张名为“量子计算机的工作原理”的图片。 因此,有意简化了本文中的许多概念,以便在“基本”级别更好地理解量子技术,但并没有因信息内容和充分性的丧失而大大简化 。
在某些地方,本文使用了其他来源的材料,本文末尾列出了这些材料的清单 。 尽可能插入指向原始文本,表格或图片的直接链接和参考。 如果某个地方我忘了某事(或某人),请写-我会改正。
引言
(到内容)
在本章中,我们将简要介绍量子时代是如何开始的,这是量子计算机概念的动力,量子计算机的思想家(哪些国家和公司)目前是该领域的主要参与者,并简要讨论了量子计算发展的主要方向。
一切如何开始
(到内容)

量子时代的参考点被认为是1900年,当时普朗克(M. Planck)首次提出了这样的假设 :能量的发射和吸收不是连续的,而是在单独的量子(部分)中进行的。 当时许多杰出的科学家-玻尔,爱因斯坦,海森堡,薛定ding提出并提出了这个想法,最终促成了量子物理学等科学的创造和发展。 在网络上,关于量子物理学作为一门科学的发展有很多很好的材料,在本文中,我们将不做详细介绍,但是有必要指出我们进入新量子时代的日期。
量子物理学将许多发明和技术带入了我们的日常生活,没有它们,现在很难想象我们周围的世界。 例如,现在从家用电器(激光水平仪等)到高科技系统(视力矫正激光器,hello meklon )到处都使用的激光器。 逻辑上假设某人迟早会提出为什么不使用量子系统进行计算的想法。 因此在1980年发生了。
维基百科显示,科学家尤里·马宁(Yuri Manin)于1980年率先表达了量子计算的思想。 但是直到1981年,他们才真正开始谈论它,当时著名的R.Feynman在麻省理工学院举行的第一届计算物理学会议上的报告中指出,不可能有效地在经典计算机上对量子系统的演化进行建模。 他提出了能够进行这种模拟的量子计算机的基本模型。
在网络上有这样的工作 ,其中在学术上和细节上都对量子计算的发展进行了时间顺序的研究 ,但我们将简要介绍一下:
量子计算机历史上的里程碑:
如您所见,从构想之初到在2个量子比特的计算机中首次实现它已经过去了17年(从1981年至1998年),而从量子比特的数量增加到53年已经过去了21年(从1998年到2019年)。 从11到11的时间(从2001年到2012年),Shore算法的结果(我们将进一步讨论)从15改进到21。而且,仅在三年前,我们才意识到Feynman所说的,并且学习模拟最简单的物理系统。
量子计算的发展缓慢。 科学家和工程师面临着非常复杂的任务,量子态非常短暂且脆弱,为了使它们保持足够长的时间来进行计算,人们必须花费数千万美元建造石棺,其中温度要保持在绝对零以上,并且要防止温度升高。外部影响。 此外,我们将更详细地讨论这些任务和问题。
领先者
(到内容)

本部分的幻灯片摘自文章《 量子计算机:一个大的提升游戏》。 俄罗斯量子中心 Alexei Fedorov的研究员在Yandex上作了演讲 。 我将允许自己直接引号:
目前所有技术上成功的国家都在积极参与量子技术的发展。 在这些研究中投入了大量资金,正在创建支持量子技术的特殊程序。

量子竞赛不仅涉及国家,而且还涉及私营公司。 近年来,谷歌,IBM,英特尔和微软总共投资了约5亿美元用于量子计算机的开发,并建立了大型实验室和研究中心。
在Habré和Web上有很多文章,例如, 在这里 , 这里和这里 ,其中更详细地考虑了各国在量子技术发展方面的当前状况。 现在对我们而言,最主要的是,所有领先的技术发达国家和参与者都朝着这个方向投入大量资金用于研究,这为摆脱当前技术僵局提供了希望。
发展方向
(到内容)

目前(我可能是错的,正确的)所有领先参与者的主要努力(或多或少有显著成果)集中在两个方向:
- 旨在解决一个特定的特定问题(例如优化问题)的专用量子计算机 。 产品的一个例子是D-Wave量子计算机。
- 通用量子计算机 -能够实现任意量子算法(肖尔,格罗弗等)。 来自IBM,Google的实现。
量子物理学为我们提供的其他发展媒介,例如:
当然也需要研究的领域,但是目前似乎有某种或多或少的重要成果。
此外,您可以在这里 , 这里和这里阅读有关量子技术发展的路线图 ,例如,谷歌“ 量子技术的发展 ”。
基础知识。 量子物体和量子系统
(到内容)

从本节中了解的最重要的事情是
量子计算机 (与传统计算机相反)使用量子对象作为信息载体,并且量子对象必须连接到量子系统才能执行计算。
什么是量子物体?
量子对象是表现出量子性质的微世界(量子世界)的对象:
- 具有两个边界级别的特定状态
- 在测量之前,它一直处于状态叠加状态
- 与其他物体纠缠在一起以创建量子系统
- 执行克隆禁止定理(无法复制对象的状态)
让我们更详细地分析每个属性:
具有两个边界级别的特定状态(最终状态)
现实世界中的经典例子是硬币。 她处于“侧面”状态,该状态具有两个边界级别:“鹰”和“尾巴”。
在测量之前,它一直处于状态叠加状态
抛硬币,它飞行并旋转。 在旋转时,无法说出其“侧面”状态位于哪个边界层。 但是,如果我们猛然抨击并观察结果,状态的叠加将立即崩溃为两个边界状态之一-“头”和“尾”。 在我们的案例中,砸硬币是一个维度。
与其他物体纠缠在一起以创建量子系统
硬币很难,但请尝试。 想象一下,我们扔了三枚硬币,使它们彼此紧紧地旋转,例如硬币的杂耍。 在每个时刻,不仅它们中的每一个处于状态的叠加,而且这些状态相互影响(硬币碰撞)。
执行克隆禁止定理(无法复制对象的状态)
当硬币在飞行和旋转时,我们决不能创建与系统分离的任何硬币的旋转状态的副本。 该系统自身存在,并且非常嫉妒提供任何信息。
关于“叠加”这一概念的几句话,几乎在所有文章中,叠加都被解释为“同时处于所有状态”,这是正确的,但有时太令人困惑了。 状态的叠加也可以认为是这样的事实,即量子对象在每时每刻都有一定的概率塌陷到其每个边界能级中,并且这些概率合计自然等于1 。 此外,在考虑量子比特时,我们将对此进行更详细的介绍。
对于硬币,这可以从视觉上想象出来-取决于初始速度,抛掷的角度,硬币飞行的环境状态,在每个时刻获得“鹰”或“尾巴”的可能性是不同的。 而且,如前所述,可以将这种飞行硬币的状态想象为“同时处于其所有边界状态,但实施它们的可能性不同”。
满足以上属性并且我们可以创建和管理的任何对象都可以用作量子计算机中的存储介质。
再进一步,我们将讨论量子位作为量子对象的物理实现的当前事务状态,以及科学家现在以这种身份使用的东西。
因此,第三个属性表明,可以纠缠量子对象以创建量子系统。 什么是量子系统?
量子系统是具有以下性质的纠缠量子物体的系统:
- 量子系统处于由其组成的物体的所有可能状态的叠加中
- 在进行测量之前,不可能知道系统的状态
- 在测量时,系统会实现其边界状态的可能变体之一
(并领先一点)
量子程序的推论 :
- 量子程序在输入处具有系统的给定状态,在内部具有叠加,在输出处具有叠加
- 在测量后的程序输出中,我们对系统可能的最终状态之一(加上可能的错误)进行了概率实现
- 任何量子程序都具有烟囱结构(输入->输出。没有循环,您无法在过程的中间看到系统的状态。)
量子计算机与常规计算机的比较
(到内容)

现在让我们将传统计算机与量子计算机进行比较。
逻辑层

在普通计算机上,这有点。 众所周知的确定性位 。 它可以取0或1的值。它可以很好地满足常规计算机的逻辑单元的作用,但是完全不适合描述量子对象的状态,正如我们已经说过的那样,在假设其边界状态的情况下,这种状态很普遍 。
为此,发明了一个量子比特 。 在其边界状态下,它实现类似于0和1的状态| 0>和| 1> ,并且叠加起来表示在其边界状态 |0>和|1>的概率分布 :
a|0> + b|1>, , a^2+b^2=1
在这种情况下,a和b表示概率的幅度 ,而其模块的平方实际上表示如果量子位因当前的测量而塌陷,则实际上精确获得边界状态|0>和|1>,值的概率 。
身体水平
在当前的技术发展水平上,常规计算机的物理实现是一个半导体晶体管 ,对于一个量子,正如我们所说的,它是任何量子对象 。 在下一节中,我们将讨论现在用作量子位的物理载体的东西。
储存介质
对于常规计算机,这是电流 -量子的电压电平, 电流的存在与否等- 量子对象的恰好状态 (极化方向,自旋等),可能处于叠加状态。
运作方式
为了在常规计算机上实现逻辑电路,我们都使用了众所周知的逻辑运算 ;对于量子位的运算,我们必须提出一种完全不同的运算系统,称为量子门 。 门是单量子位和两个量子位,具体取决于要转换的量子位数量。
量子门的例子:
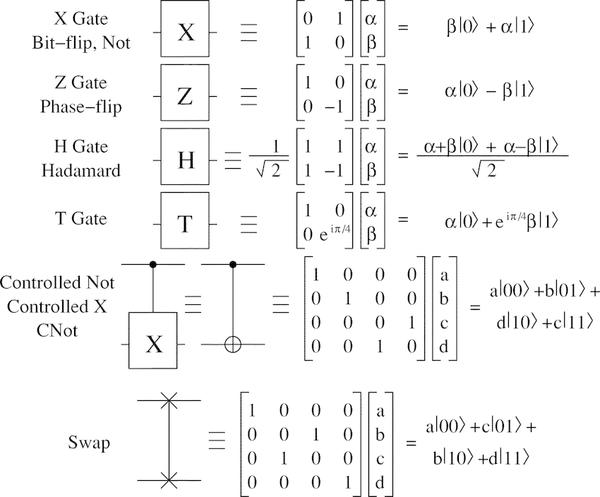
通用门的概念是存在的 ,它足以执行任何量子计算。 例如,通用套件包括Hadamard阀,相移阀,CNOT阀和π⁄8阀。 在他们的帮助下,您可以对任意一组量子位执行任何量子计算。
在本文中,我们将不对量子门系统进行详细介绍;例如,有关量子门和量子位的逻辑运算的详细信息,请参见此处 。 要记住的主要内容:
- 量子对象上的运算需要创建新的逻辑运算符(量子门)
- 量子阀为单量子位和二量子位
- 有通用的门组,您可以用它们执行任何量子计算
对接
一个晶体管对我们完全没有用,要进行计算,我们需要将许多晶体管彼此连接起来,也就是说,要用数百万个晶体管创建一个半导体芯片,我们已经在其上构建了逻辑电路, ALU,并最终获得了经典形式的现代处理器。
一个量子位对我们也完全没用(嗯,如果只是从学术角度来说),
为了进行计算,我们需要一个量子位系统(量子对象)
正如我们已经说过的那样,它们是通过纠缠量子位来创建的,从而使它们的状态发生变化。
演算法
人类迄今为止积累的标准算法完全不适合在量子计算机上实现。 是的,一般而言,没有必要。 基于量子位上的门逻辑的量子计算机需要创建完全不同的算法,即量子算法。 在最著名的量子算法中,可以区分三种:
原理
最重要的区别是工作原理。 对于标准计算机,这是一个严格确定的数字原理 ,基于以下事实:如果我们设置系统的某些初始状态并将其通过给定算法,则无论我们执行此计算多少次,其计算结果都将相同。 实际上,这种行为正是我们对计算机的期望。
量子计算机以模拟,概率原理运行 。 在给定的初始状态下,给定算法的结果是该算法最终实现的概率分布的样本加上可能的错误。
量子计算的这种概率性归因于量子世界的非常概率性。 老爱因斯坦说: “上帝不会与宇宙玩骰子 。”但到目前为止(在目前的科学范式中)所有的实验和观察都证实了相反的观点。
量子位的物理实现
(到内容)

正如我们已经说过的,量子位可以由量子对象表示,即实现上述量子属性的物理对象。 也就是说,粗略地说,具有两个状态并且这两个状态处于叠加状态的任何物理对象都可以用来构建量子计算机。
“如果我们可以将一个原子置于两个不同的级别并对其进行控制,那么这里就是您的一个量子比特。 如果我们可以用离子来做,那就是量子比特。 与当前相同。 如果我们同时顺时针和逆时针运行它,这是一个量子比特。” (C)
这篇文章有一篇精彩的评论 ,其中详细介绍了当前各种qubit的物理实现,但是我们只列出最著名和最常见的:
在所有这些多样性中,最复杂的第一种基于超导体产生量子位的方法。 Google , IBM , Intel和其他领先厂商都使用它来构建他们的系统。
好吧,还请阅读安德鲁·戴利(Andrew Daley)2014年 对量子位可能的物理实现的评论 。
基础知识。 量子计算机的工作原理
(到内容)

本节的材料(任务和图片)摘自“仅此而已。 量子计算机是如何工作的 。 ”
因此,让我们假设我们有以下任务:
一共有三个人: (A)ndrey,(B)olodya和(C)异端 。 有两辆出租车(0和1) 。
还众所周知:
- (A)ndrey,(B)olodya-朋友
- (A)恩德雷(C)异端-敌人
- (B)奥洛迪亚(C)异端-敌人
任务:乘出租车让人们坐下,以便最大(朋友)和最小(敌人)
分数: L =每个住宿选项的(朋友数量)-(敌人数量)
重要说明:假设没有启发式方法,也没有最佳解决方案。 在这种情况下,仅通过彻底搜索选项即可解决该问题。
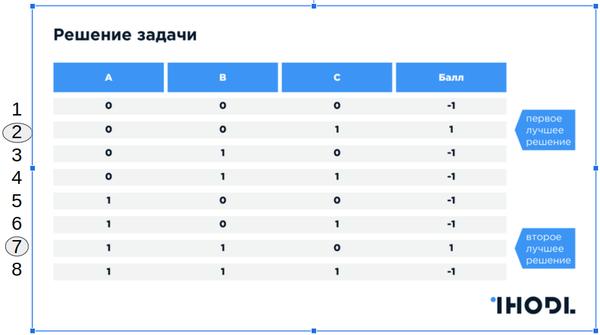
普通计算机上的解决方案
如何在常规(超级)计算机(或群集)上解决此问题-显然, 我们需要循环搜索所有可能的选项 。 如果我们有一个多处理器系统,那么我们可以并行计算多个处理器上的解决方案,然后收集结果。
我们有2个可能的住宿选择(出租车0和出租车1)和3人。 解的空间为2 ^ 3 = 8 。 您甚至可以在计算器上浏览8个选项,这不是问题。 现在我们将使任务复杂化-我们有20个人和两辆公共汽车,解决方案空间为2 ^ 20 = 1,048,576 。 让我们将人数增加2.5倍-乘坐50人并乘两列火车,现在的决策空间为2 ^ 50 = 1.12 x 10 ^ 15 。 常规(超级)计算机已经开始出现严重问题。 我们会将人数增加2倍,而100人将为我们提供1.2 x 10 ^ 30种可能的选择。
在合理的时间内,一切都无法算作这项任务。
我们连接一台超级计算机
目前功能最强大的计算机是Top500的第一名,它是Summit ,容量为122 Pflops 。 假设对于一个选项的计算,对我们来说100个操作就足够了,然后为100个人解决问题,我们需要:
(1.2 x 10 ^ 30100)/ 122x10 ^ 15 /(60 60 24 365)= 3 x 10 ^ 37年。
如我们所见, 随着源数据维数的增加,解的空间根据幂定律增长 ,一般情况下,对于N位,我们有2 ^ N个可能的解,它们的N相对较小(100),给我们提供了一个不可读的空间(在当前技术水平上)决定。
有其他选择吗? 您可能已经猜到了,是的。
但是,在继续介绍量子计算机如何以及为何能够有效解决此类问题之前,让我们先回顾一下概率分布是什么。 别担心,这篇评论文章将不会有硬性数学,我们将为您提供一个带袋和球的经典示例。
相当多的组合学,概率论和奇怪的实验者
拿一个袋子放1000个白色和1000个黑色的球 。 我们将进行实验-取出球,记下颜色,将球放回包中,然后将球混入包中。
我们进行了10次实验, 抽出10个黑球 。 也许吧 挺好的 这个样本能给我们一些合理的概念,说明袋子中的真实分布吗? 显然不是。 您需要做的是正确的, 重复实验一百万次,并计算出黑白球坠落的频率。 例如,我们得到49.95%的黑色和50.05%的白色 。 在这种情况下,我们采样所依据的分布结构已经或多或少清晰了(我们取一个球)。
您需要了解的主要内容是, 实验本身具有概率性质 ,对于一个样本(球),我们无法识别出真正的分布结构,因此需要重复多次实验并对结果取平均值。
在我们的书包中添加10个红色和10个绿色的球 (错误)。 重复实验10次。 中拉5红5绿 。 也许吧 是的 我们可以说一些关于真实分布的问题-不。 需要做什么-好吧,您了解。
为了了解概率分布的结构,有必要从该分布中反复采样单个结果,并对结果取平均值。
我们将理论与实践联系起来
现在,让我们代替台球,将1000个2号球,1000 7号球和10个其他球放入袋中。 想象一个经过简单步骤训练的实验者(拿一个球,写下数字,将球放回包中,将球混入包中),他在150微秒内完成了操作。 好吧,这样的实验者可以辅助(不是毒品广告!!!)。 然后在150秒内,他将能够进行100万次实验,并为我们提供平均结果。
他们坐在实验者的手中,把袋子给了,转身走,等待了150秒-收到:
数字2-49.5%,数字7-49.5%,其余数字为1%。
是的,没错, 我们的包是一台量子计算机,其算法可以解决我们的问题 ,球是可能的解决方案。 由于有两个正确的解决方案,因此量子计算机将为我们提供所有这些可能的解决方案的可能性均等,以及0.5%(10/2000)的错误 ,我们将在后面讨论。
要获得量子计算机的结果,您需要对相同的输入数据集重复运行量子算法,并对结果求平均值。
量子计算机的可扩展性
现在,假设对于一个有100个人参与的问题(我们记得这个决策空间2 ^ 100 ),只有两个正确的解决方案。 然后,如果我们取100个量子位,并编写一个算法来计算这些量子位的目标函数(L,请参见上文),我们将得到一个袋子,其中包含1000个球,第一个正确答案的编号,1000个第二个正确答案的编号,以及10个球与其他数字。 而我们的实验人员将在同样的150秒内估算出正确答案的概率分布 。
相对于解空间(2 ^ N)的维数,可以将量子算法的执行时间(带有一些假设)视为常数O(1)。
恰恰是量子计算机的这一特性-关键在于执行时间相对于决策空间复杂度的恒定性,而决策空间的复杂度根据幂定律而增长。
量子位和平行世界
这是怎么发生的? 是什么让量子计算机如此快速地进行计算? 这完全与量子位的量子性质有关。
瞧,我们说过,当量子比特被观察到时,它就实现了它的两个状态之一 ,但是在“生命自然”中,它处于状态的叠加状态 ,也就是说,它同时处于两个边界状态(有可能)。
拿(A)Ndrey并想象他的状况(车辆为0或1)作为一个量子比特。 然后,我们(在量子空间中)有两个平行的世界 ,一个(A)坐在出租车0中,另一个世界在出租车1中。 同时在两个出租车中 ,但有机会在观察时在每个出租车中找到它。
拿(B)olod并把他的状态想象为一个量子比特。 出现了另外两个平行世界。 但是,尽管这两个世界(A)和(B)没有任何相互作用。 创建连接的系统需要做什么? 没错,您需要连接(混淆)这些量子位。 我们将(A)与(B)混淆,我们得到了两个量子位(A,B)的量子系统,该量子系统在其内部实现了四个相互依赖的并行世界。 加(C)erge并得到一个三个量子位(ABC)的系统,该系统实现了八个相互依赖的并行世界。
量子计算的本质(在耦合的量子位系统上实现一系列量子门)是这样的事实,即计算同时在所有并行世界中进行。
无论我们拥有2 ^ 3或2 ^ 100多少个量子算法 , 量子算法都会在有限的时间内在所有这些并行世界上执行并给出结果,这是该算法答案的概率分布中的一个示例。
为了更好地理解,我们可以想象一个量子计算机在一个量子水平上启动2 ^ N个并行决策过程 ,每个决策过程都在一个可能的选项上工作,然后收集工作结果,并以解的叠加形式给出答案 (答案的概率分布),从我们每次(在每个实验中)都采样一次。
请记住,我们的实验人员进行实验所需的时间(150μs) ,当我们谈论量子计算机的主要问题和退相干时间时,这将派上用场。
量子算法
(到内容)
如上所述,基于二进制逻辑的常规算法不适用于使用量子逻辑(量子门)的量子计算机。 对他来说,他必须提出新的方法,以充分利用计算的量子本质所固有的潜力。
当今最著名的算法是:
与经典计算机不同,量子计算机不是通用的。
迄今为止,仅发现了少量的量子算法。 (C)
感谢oxoron链接到Quantum Algorithm Zoo ,据作者( Stephen Jordan ) 所说 ,这里是量子算法世界最好的代表已经聚集并继续聚集的地方。
在本文中,我们不会详细分析量子算法,Web上有很多关于各种复杂程度的优秀材料,但是您仍然需要简要介绍一下三个最著名的材料。
肖氏算法。
(到内容)
最著名的量子算法是Shor算法 (由英国数学家Peter Shor于1994年发明),旨在解决将数字分解为素因数的问题(分解问题,离散对数)。
当他们写道您的银行系统和密码将很快被黑客入侵时,以该算法为例。 考虑到当今使用的密钥长度不少于2048位,上限的时间尚未到来。
迄今为止, 结果并不算适中。 使用Shore算法的最佳分解结果是数字15和21 ,该数字远小于2048位。 对于表中的其余结果,使用了不同的计算算法 ,但是即使根据该算法的最佳结果(291311)也与实际应用相去甚远。
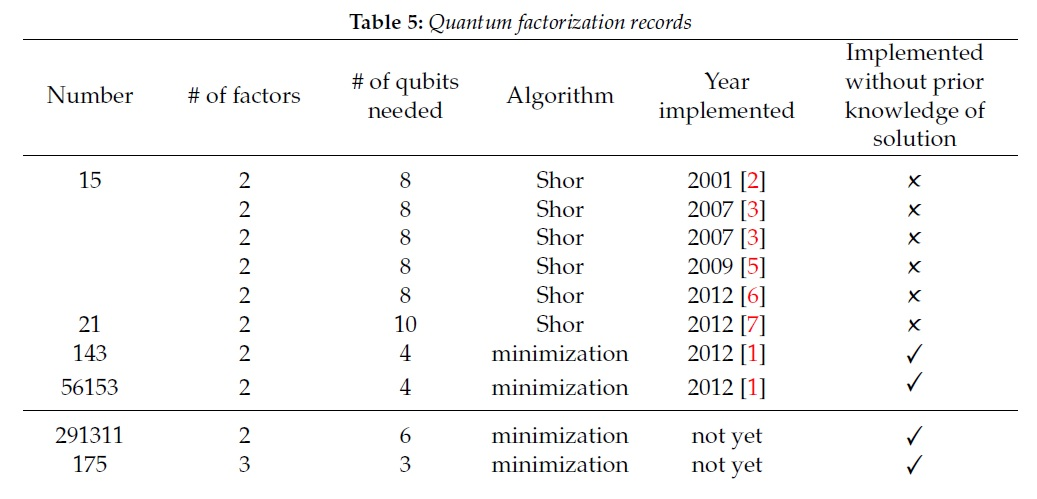
例如,您可以在此处阅读有关Shore算法的更多信息。 关于实际实施- 在这里 。
当前估计要分解2048位数字所需的复杂性和功能之一是一台具有2000万量子位的计算机。 我们安静地睡觉。
格罗弗算法
(到内容)
Grover算法是用于解决枚举问题的量子算法 ,也就是说,找到方程F(X) = 1 ,其中F是n个变量的布尔函数 。 它是由美国数学家洛夫·格罗弗 ( Lov Grover)在1996年提出的 。
Grover的算法可用于查找数字序列的中位数和算术平均值 。 另外,它可以通过在许多可能的解决方案中穷举搜索来解决NP完全问题。 尽管通常不提供“ 多项式解决方案 ”,但与传统算法相比,这可以显着提高速度 。 (C)
您可以在此处或此处阅读更多内容。 在箱子和球的示例中也对算法进行了很好的解释,但是不幸的是,由于我无法控制的原因,该站点无法从俄罗斯向我开放。 如果您的网站也被阻止,那么请进行以下简要介绍:
Grover的算法。 想象一下,您有N个带编号的封闭盒。 除了球所在的球以外,它们都是空的。 您的任务:找出球所在的盒子的编号(这个未知的数字通常用字母w表示)。

如何解决这个问题? 以最愚蠢的方式,轮流打开盒子,迟早您会碰到一个带球的盒子。 , ? N/2. , 100 , 100 , , .
. , , (Oracle). — « 732», « 732 ». , , « , »
, , , : N SQRT(N) !
.
-
( )
— ( — ) — [ ]( https://ru.wikipedia.org/wiki/%D0%9A%D0%B2%D0%B0%D0%BD%D1%82%D0%BE%D0%B2%D1%8B%D0%B9 %D0%B0%D0%BB%D0%B3%D0%BE%D1%80%D0%B8%D1%82%D0%BC), 1992 , , . _
— , F(x1, x2, … xn) ( 0, 1 ) ( 0, 1). , , . ()
. :
( — ) , . , . : «» «» – , «», «» — . , , – . ()
( )

, . ( ) :
“ ”, .
:
( )
N+1 .
, , ( ) . , , — .
, (-273.14 ) - , () .
, , .
.
, . — IBM IBM Q System One Google Sycamore . , (2) 200 .
Sycamore, — 1 200 , — 130 . 150 . ? .
?
, 150 N — .
:
150 . — .
...
( )

, , 100% , - . , . :
, , , . , , . , , , .
— () , , , . — “ ?” — 5050, .
, ( ) - . . N 1 .
— . , 100 , 80 , 20.
— , . .
. , — IBM IBM Q System One Google Sycamore :
— . 1-Fidelity. , 2- .
2016 NQIT .
( )

, . () , , .
1- , , 12-, , , . , , , , .
, , , “ ” “” . .
:
, , . , , . - , .
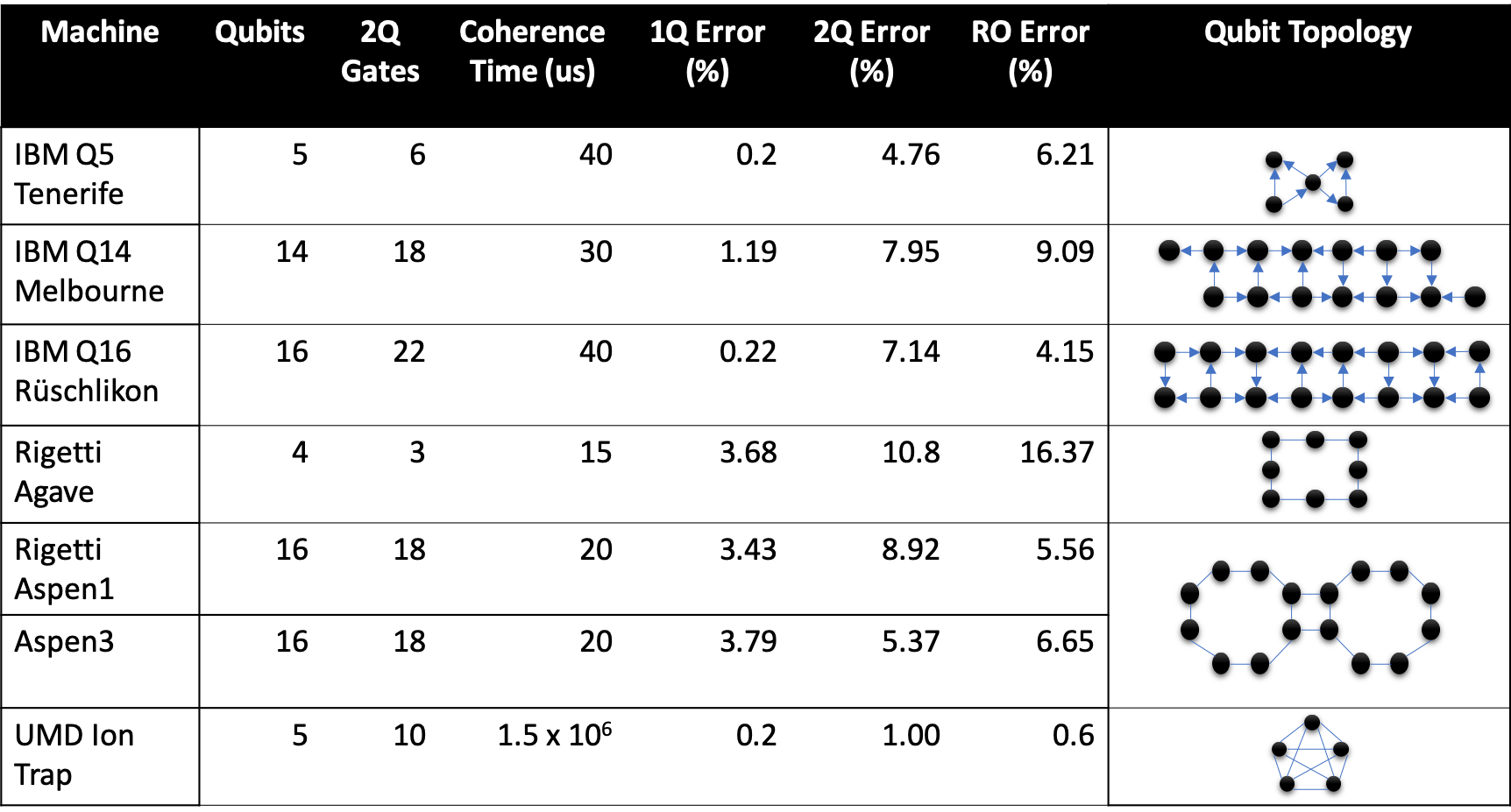
:
( )
— . 150 :
, 0.5 , :
We measure a qubit coherence time in excess of 0.5 s, and with magnetic shielding we expect this to improve to be longer than 1000 s
, , .
, , , .
, , , 1 4 1 6.
( )
, :
, , ( ) , . ( ), , .
D-Wave
( )

2000- D-Wave 2000Q. : D-Wave Systems
Google 53- , D-Wave, , . , 53 , 2048 ? ...
( ):
D-Wave ( ), , .
, , , (, ), Scott Aaronson . , ,
D-Wave. , 2014 IBM , D-Wave . , 2015 Google NASA , , , . Google , , .
, D-Wave, . , . , — . , D-Wave ASIC .
( )
. , :
- , 232 264 (8-16 )
- N 2^N , .. 2^(3+N) 32- 2^(4+N) 64- .
- N 2^N x 2^N
:
()
, Summit ( Top-1 Top-500 ) 2.8 .
— 49 ( Sunway Taihu Light )
.
. :
— 49 - 39 "" ( ) 2^63 — 4 4
50+ . - Google 53- .
.
(到内容)

:
́ ́ — , .
, , , , , . .
, “ ”. , 50+ , , , . .
, . , Google, Sycamore .
Google
(到内容)

54- Sycamore
, 2019 Google Nature « ». 54- «Sycamore».
Sycamore 54- , 53-. , , 54- , . , 53- .
, .
IBM , Google . , 2,5 , , . .
, , Scott Aaronson . Scott's Supreme Quantum Supremacy FAQ! , . FAQ, , , .
Google? , :
, , , . : (.. 1- 2- — — , 20, 2D n=50-60 ). , 0, {0,1}, n- () . , , .
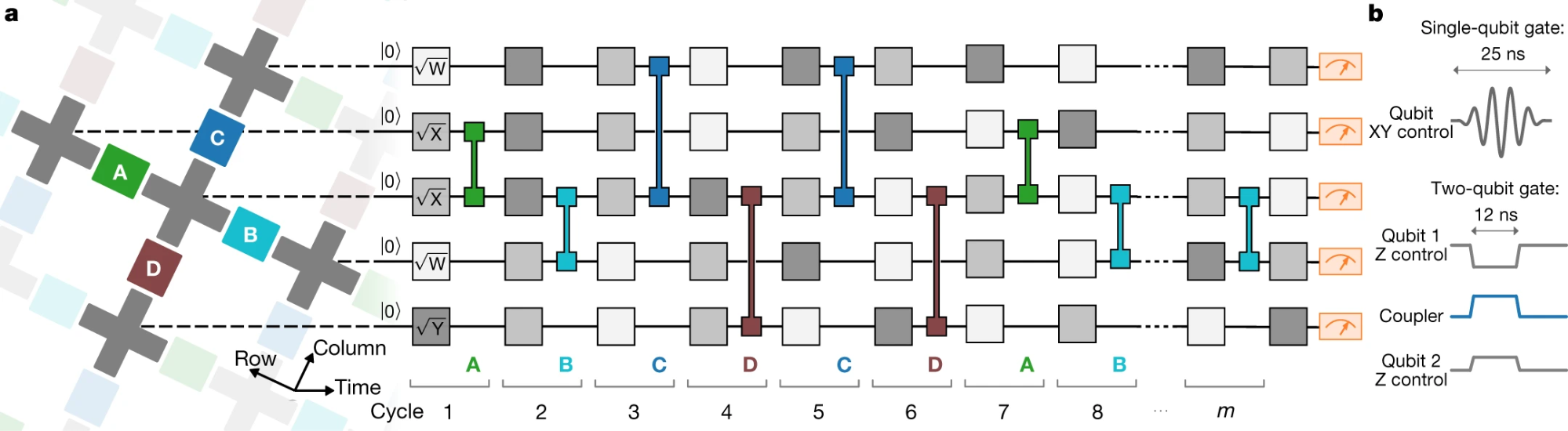
:
Google 53- , .
— Google , , , , , . , 2048- .
总结
(到内容)

— , .
(-) :
:
:
:
( ), , - , .
— , , . .
结论
(到内容)
, , , , D-Wave Google .
(, , ..) , , , , .. , .
, - .
() Kruegger
(到内容)

@Oxoron , “ ”
@a5b - “ ” , , .
, .
(到内容)

[The National Academies Press]