诗歌是一个非常美丽的,通常经过深思熟虑的音节,我们在日常生活中不使用它,但喜欢那样享受它。 数学也可以这样说。 在影片《 Pi》中,主人公称数学为“自然语言”,在影片“心灵游戏”中,主人公称其为“特殊艺术形式”。 在日常生活中,我们可以完全忘记它。
即使在二维维度上,奇怪的吸引子的外观也是异常且有吸引力的。 通过Plotly,您可以在三个维度上构建它们,并使其非常容易获得可以“扭曲”并可以通过其“飞行”(即“触觉”)的3D模型。

一切如何开始
这一切都始于很久以前,2007年,在大学的某个地方,我熟悉了自组织理论,并且我第一次在书中看到了洛伦兹吸引子,其黑白插图。 然后,在我看来,奇怪的是,某些东西会沿着这种不寻常的轨迹运动。 对我来说甚至更陌生的想法似乎是,世界上几乎所有事物都可以用一个理论来描述。
总的来说,一切都像往常一样-我的世界观发生了变化,生活在继续,时间在过去。 现在,最近一次,我遇到一个
链接 ,看到了:
 图片来自chaoticatmospheres.com
图片来自chaoticatmospheres.com“美丽。”我想。 所有这些都可以在Matplotlib中构建的想法也浮出水面,但是我已经事先知道,没有什么壮观的方法可以起作用。 就在最近的两周前,我认识了Plotly,并立即意识到可能会有所收获。
立即进行的首次尝试失败。 事实证明,“奇异吸引者图库”的某些图像上的公式包含错误。 但是,画廊的作者诚实地警告说,他不是数学家,就像本文的作者一样。
简短的“ google”使得找到此
代码成为可能,该
代码非常有用,由Michael Tyka创建。 这个很棒的人为Blender制作了一个完整的插件,使您可以构建60个吸引器的模型(!)。 实际上,它们可以在3D打印机上打印,并且鉴于有蜡打印技术,因此很容易获得用于铸造青铜的模具。
可视化代码
好吧,除了是一名业余数学家外,我还是一名业余程序员。 因此,请勿严格根据代码的质量进行判断。
结果,应该出现一个名为
Lorenz Mod 1的奇异吸引子的3D模型:

应当立即指出,为了求解微分方程组,从SciPy模块中选择了
odeint函数,在我看来这是创建工作代码的最简单,最快的方法。 但是,所有方程都可以通过通常的欧拉方法求解。
为了表示代码中的系数,出于习惯,我使用了LaTeX中采用的希腊字母的名称。 在使用Jupyter笔记本时,这有时非常有用,因为公式可以很快变成代码,并且代码可以很快变成公式。
如果您不熟悉Python生态系统,但希望确保代码能够运行,那么最好安装最新版本的Python
Anaconda发行版,而conda的Plotly软件包是内置的发行软件包管理器。
鉴于数量众多的奇异吸引子,似乎不可能全部构建它们。 因此,在本文中,我将仅介绍我设法构建的那些最有趣的东西。
Chen-Lee吸引者

蔡氏吸引器

库尔吸引子

达德拉吸引者

李德全吸引器

财务吸引人

四翼吸引子

哈德利吸引者
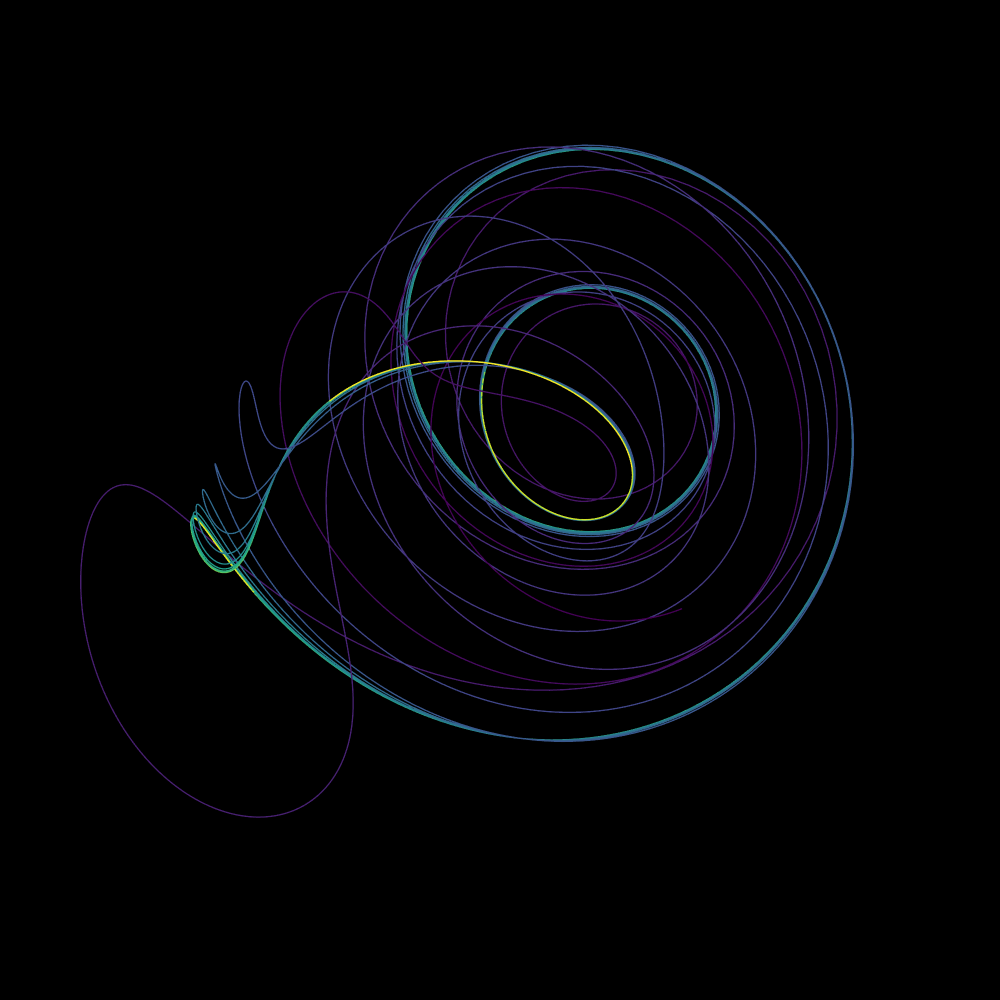
Halvorsen吸引子

柳尘吸引人

Lorenz Mod 2吸引器

修改后的蔡氏混沌吸引子

牛顿莱普尼克吸引器

鼻胡吸引器
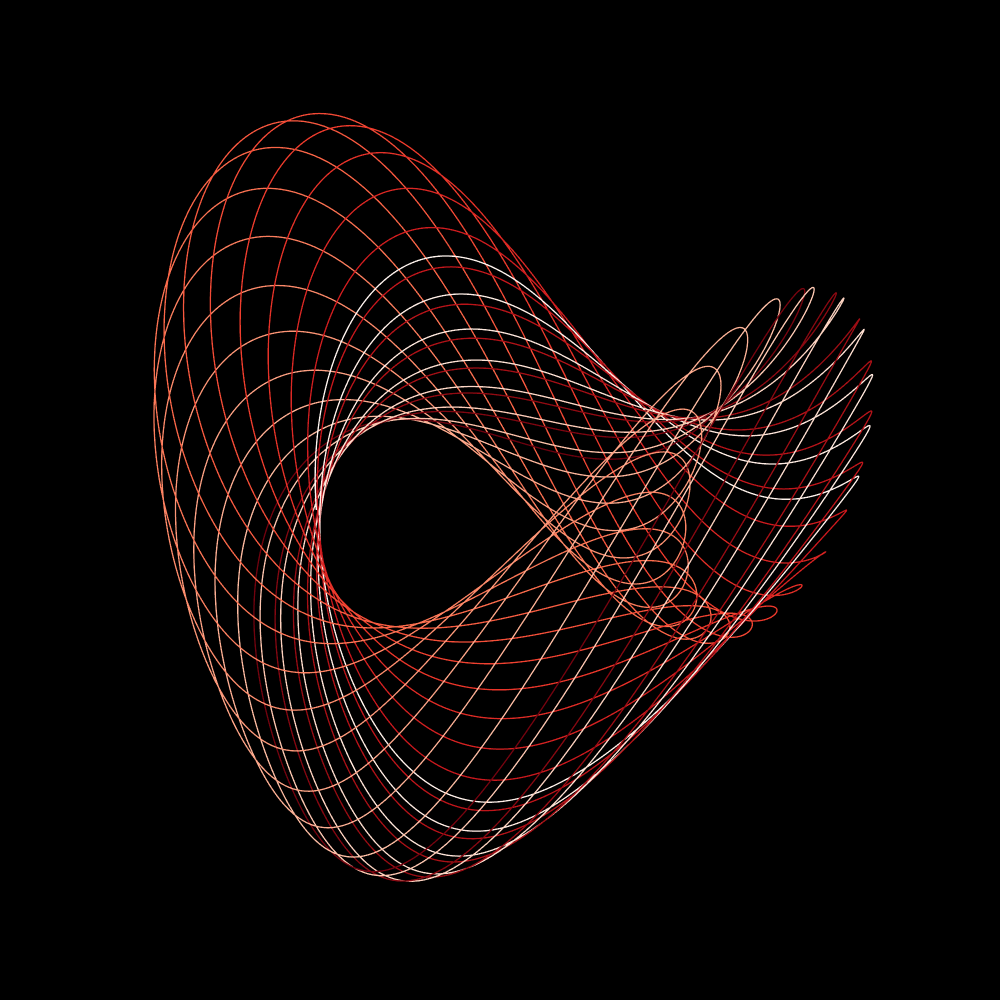
罗斯勒吸引器

萨卡里亚吸引人

托马斯吸引器

三涡旋统一混沌系统吸引子(TSUCS1)

王孙吸引子

总结
火,水,地球,天空,太阳,月亮,星星-所有这些都是最古老的诗意精华。 很多时候,我设法找到数学上同样漂亮的东西。 但是很多时候我什至不了解如何用数学语言和普通语言来谈论所有这些。 我不懂,但我想学习。
但是我100%意识到,现代的可视化工具提供了一个绝佳的机会来表达您对当前正在做的事情的态度,并有机会展示这对您有多么重要以及您有多有趣。 一言不发。