爱因斯坦-波多尔斯基-罗森的悖论现已在世界上许多实验室和科研机构中得到积极研究。 正在撰写大量科学文章。 在近科学界引起了很多炒作。
尽管很矛盾,但只有一个障碍。 在量子力学本身中,EPR悖论没有任何悖论! 不是克!
那么为什么要对其进行如此仔细的研究呢?
是的,以太与它有什么关系?
寻找新的物理学
答案很简单-在研究EPR悖论时,人们正在积极寻找新的物理学。 准确地说-随着应用物理学的发展,人们正在寻找新的基础物理学。
在我们的世界中尤其如此,在这个世界中,球是由阴谋论统治的,这些阴谋论暗示着某个地方的爬行动物或犹太人正在隐藏真实的物理学!
到19世纪末,当许多物理学家认为几乎所有事物都是开放的时,它一直与之形成对立。
现在,恰恰相反,即使是保守的物理学家也认为基础物理学还远远不够完善。
自然地,寻找新物理的兴趣现在变得巨大!
有一件事情有待理解:如何确定在哪里寻找新物理学的黄金脉络?
一种选择是找出理论上的不一致之处并尝试从中进行挖掘。
以麦克斯韦的电动力学理论为例。 该理论与所有公认的理论非常吻合,没有什么可寻找的。 而且不要看。 好吧,除了统一的理论。 下午着火了,您不会找到有关基础电动力学的新文章。 虽然适用-一堆。
STO和GO的协调
但是,电动力学很难在手指上很好地显示出来,因此让我们简单一些。
让我们看看狭义相对论与古典力学(主要是伽利略的相对论)的吻合程度如何。
伽利略的相对论尤其谈到了速度的相对论。
狭义相对论特别声称光速是绝对的。
冲突似乎很明显。 但是我们(以爱因斯坦的名义)宣称STR是GO的广义理论,其中伽利略的相对论只是一个特例。
确实,如果在洛伦兹变换中我们将光速指向无穷大

,则得到伽利略变换。 换句话说,对于比光速低得多的速度,伽利略的变换将是有效的。
因此,在经典力学和特殊力学的交界处寻找新的物理学是不值得的。 而且关于这个主题的新鲜文章很少。 这并不意味着在服务站中已经挖完所有东西。 例如,您可以在tachyons(速度高于光速的粒子)领域中搜索一个新的,是的,它们正在寻找。
量子力学与经典力学的连贯性
但是,量子力学和经典力学的一致性又如何呢?
古典力学特别声称,粒子在这里和现在都存在。
量子力学声称粒子是波,在时间,空间,甚至对我们自己身上都是模糊的。
在这里,冲突也很明显。 但是您也可以走出去:我们宣布KM为经典(牛顿)力学的广义理论。
确实,如果在Schrödinger方程的解中,我们将(简化的)普朗克常数拍到零

然后我们得到牛顿定律。 好吧...几乎。
换句话说,如果我们在比德布罗意波长大得多的距离上工作,则可以使用牛顿方程。 好吧...几乎。
实际上,这还不够。 最不可理解的是-我们不知道除了波动函数的崩溃之外,量子力学中还需要改变什么,以便获得牛顿力学。

两种理论之间最明显和最简单的矛盾之一就是薛定inger猫悖论。
薛定ding悖论指出,如果我们采取一个放射性原子,并在其旁边放置一个辐射探测器作为雷管(毒药或炸弹)。 该设备旁边的那只猫:
- 根据经典力学-它将会是OR生存或死亡
- 根据量子力学-如果带有设备的猫在不可穿透的盒子中-那么-同时还活着和死了,只有信息的发布才会迫使您切换到OR / OR模式
似乎已经找到,去挖了新物理学的金矿,但并不是那么简单。
事实是,矛盾之处在于袋鼠世界悖论(实际上是罗素茶壶的复杂悖论)。
他声称,当我们闭上眼睛并关闭电器时,周围的一切都会变成袋鼠。 但是,如果我们打开电器或睁开眼睛,一切都会变成我们所看到的。
矛盾的是,这些世界在原则上既不能被证明也不能被反驳,通常会被奥卡姆的剃刀丢弃。
这意味着,尽管我们发现了量子力学与牛顿力学之间的差异-无处可查-不能进行任何一个实验来证明或否定其中一个版本。
寻找新的物理学和以太
实际上,以太的黄金时代已经消亡了一个多世纪。 以太起了对光,电场和磁场的解释的辅助作用。 但是在19世纪下半叶,当麦克斯韦(Maxwell)添加安培方程组并将电和磁的基本方程组合并为一个系统时,以太星的光芒最为明亮。这产生了电磁学理论。
求解这些微分方程,特别是,发现存在电磁波并且这些波以恒定速度运动

在哪里

-磁性和

-真空的介电常数。 不久之后,结果证明该速度与即将测量的光速非常相似,由此得出的结论是光是麦克斯韦的电磁波。
但是,该语句本身有两个缺点:
- 当我们谈论波浪时,是指这些波浪在其中传播的环境。 海浪-在水上,声音-在空中。 电磁波在什么地方传播?
- 匀速波的运动显然与伽利略速度的相对性相反。
如果第一个是更哲学的问题,那么在第二种情况下,某些事情是不正确的。
要么是伽利略是对的(速度的相对原理太矛盾了),要么是麦克斯韦是对的(尽管更直观地更正确-diff-ur的解决方案或显而易见的原理?!),或者两者都是对的(改变diff-ur仍然非常困难装在伽利略号下)。

发光醚的理论消除了所有张力-首先,事实证明,电磁波在醚上传播,并且光速相对于固定醚是恒定的,但是醚本身的运动是相对的。 也就是说,事实证明麦克斯韦和伽利略都是正确的。 好吧...理论上。
是的,实践并没有停滞不前。 越来越精确的测量结果没有显示出光速的任何偏差,也没有检测到空风。
洛伦兹意识到以太隐藏并改变了时空,似乎没有以太风,光速是恒定的。
爱因斯坦在1905年只删除了不必要的本质,并在洛伦兹变换的基础上创建了相对论的特殊理论。 因此,以太失去了一半的功能。
最终,随着量子力学的发展,发光醚不久就不必要地死亡了,这是在1924年发现波粒对偶性。光不再需要介体,e / m波在光子本身中传播。
在非本地搜索新物理学
同样,我们正在寻找经典力学和量子力学之间的差异,但是我们可以通过实验进行确认并尝试找到一种解释。
这些是违反本地性的实验。 科学家非常确定世界是局部的(没有远程交互作用,粒子使用光子和其他规范玻色子之类的助手相互通信)。
另一方面,量子力学的某些结果显然是非局部的。
偏光的非局部效应
不,我们不会看复杂的东西,例如EPR悖论。 为了实现这一点,我们将使用一个更简单的实验-即光偏振效应的非线性。 为此,我们不需要大型的工具或机构。 到照相器材商店购买2个线性偏振滤镜就足够了。 就是这样。
为了获得经验,我们将两个滤镜彼此平行放置并用手电筒照明。 如果滤光片是理想的,那么穿过第一个滤光片的整个光束将毫无损失地穿过第二个滤光片。 如果出现停电,则将其作为常数系数单独考虑。

因此,如果第二个并行滤波器的极化相对于第一个滤波器成一定角度(反之亦然),则根据量子力学的最终透射系数为

也就是说,如果角度为零,则100%的光线通过,如果90°-光线被完全遮挡-0%的光线通过。 如果角度为45°,则光束的一半会通过50%。 等等

实践表明(19世纪初发现的马鲁斯律法)与理论非常吻合。
现在最重要的是:
如果每个粒子单独做出决策而又不与任何人交流,则这些决策不能使用局部性来解释。如果可以-继续,请填写文章并获得诺贝尔奖!
我们可以借助局部性来解释线性依赖性,以便在0°时通过100%,在45°时通过50%,在90°时通过0%。 但是,在任何其他角度下,这些值都不会收敛。
现在将有聪明的人说,让光子感应极化角,并根据公式将投下很多。 塔基(Taki)必须将实验复杂化,以实现更精确的匹配:完全独立,完全没有沟通...
爱因斯坦-波多尔斯基-罗森悖论中的非局部性
EPR悖论本身声称,可以通过违反海森堡不确定性原理同时测量量子性质,这意味着量子力学是不完整的。
玻姆建议通过纠缠的光子或电子来验证这一悖论的实验。
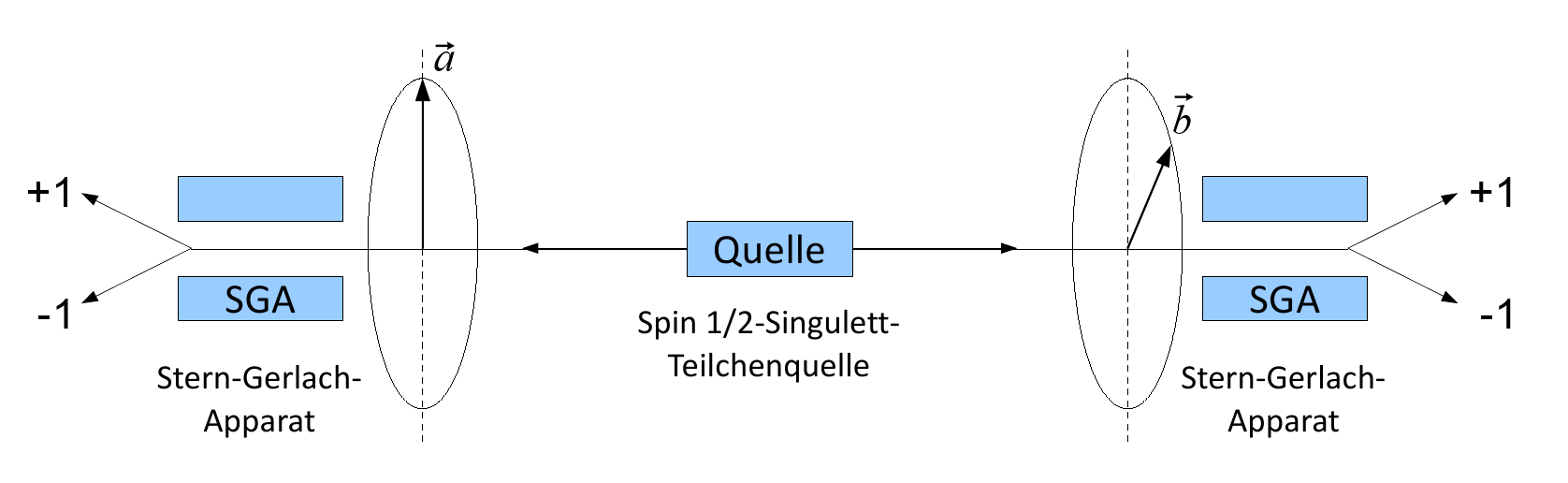
想象一个实验,其中2个电子从中心线性散射,并且都通过2个平行的自旋计。
首先,我们将了解如果电子是普通的而不是纠缠的,将会发生什么。
一切都很简单。 自旋电子将通过第一米

在50%和50%的情况下

。 通过第二-一样多。
如果我们转动仪表,将会得到什么结果?
我们将平均获得50%

和50%的病例

。 琐碎的
现在让我们复杂化并尝试查找依赖项。
让我们知道一个自旋的粒子通过了第一米

。 如果不是,则忽略通过第二个粒子的结果。 问题是万一第一个流量计是第二个流量计,它将通过第二个流量计

? 显然-概率为50%将显示旋转

并有50%的概率

。
为了方便起见,我们引入相关指数,该指数等于两个选项的概率差的模数:

我们的相关性为零。
该设备还有另一个自由度:旋转流量计可以彼此独立旋转。 如果具有自旋的粒子穿过第一米会发生什么

第二个仪表相对于第一个仪表旋转90°。 显然-平均为50%

和50%的病例

。 同样,相关性为零。
通常,无论您走到哪里,都不会产生关联。
但是,当我们发送纠缠的电子时,它变得更加有趣。
纠缠的粒子非常简单:它们始终相对于彼此反向旋转。
如果第一个旋转

,那么第二个纠缠的电子必然具有

旋转。
如果第一个旋转

然后第二个-

。
也就是说,相关性为100%。
但是,如果我们将第二个卡尺旋转90°会怎样? 如果第一个旋转

,那么第二个纠缠的电子的平均值为50%

和50%的病例

。 事实证明,相关性为零。
如果将第二个卡尺旋转45°会发生什么? 如果第一个旋转

那么第二个纠缠的电子将有25%的机会

和75%的机会

。 50%相关。
在一般情况下,我们从理论和实践中得出,相关程度取决于旋转仪的相互角度:

就是说,实际上,我们得到了与光子通过滤波器相同的非线性方程。
您可以尝试使用隐藏参数来描述局部非线性,但是会违反Bell对于隐藏随机参数的不等式。
贝尔在Clauser-Horn-Shimoni-Holt公式中的理论说,对于四个随机变量,不等式将始终为真:

其中K是没有模数的相关性(可能为负)。
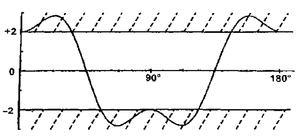
仅对于这些实验,不等式将在某些角度(接近0°和90°)处被克服,这意味着它们不能用随机的隐藏参数来解释。
结论
在古典力学和量子力学的交汇处,古典主义失去了干性。 而且它甚至使我们认为,即使在自然环境中,我们也不了解自然的地方。