三位物理学家想计算中微子的变化过程。 结果，他们发现了一些最常见的数学对象之间的意外关系。
8月的一天，早餐后的第二天早晨，数学家
陶涛（Terence Tao）打开了一封电子邮件，该电子邮件由他不熟悉的三位物理学家撰写。 三位一体向她解释说，她偶然发现了一个简单的公式，如果该公式正确，它将描述线性代数的一些最基本和最重要的对象之间的意外关系。
加州大学洛杉矶分校的教授陶（陶）说，这个公式“看起来好得难以置信”，他是
菲尔兹奖的获得者 ，
菲尔兹是世界领先的数学家之一。 他说：“很短很简单的事情早就应该在教科书中出现了，” “因此，起初我想-不，这不可能。”
然后他想了一点。
物理学家-国家加速器实验室的
斯蒂芬·帕克 （
Stephen Park） 。 费米，芝加哥大学的
张西宁和布鲁克海文国家实验室的
彼得·丹顿 （
Peter Denton）在两个月前获得了这一数学身份，试图应对称为
中微子的基本粒子的奇怪行为。
他们注意到，难以计算的“
本征矢量 ”描述了中微子在物质中的传播方式，等同于称为“本征值”的术语组合，这些术语更易于计算。 此外，他们意识到本征矢量和本征值之间的这种关系（在数学，物理学和工程学中非常普遍，自从18世纪以来就已经进行了研究）似乎具有更普遍的意义。
尽管物理学家无法相信他们已经发现了与此类基本数学有关的新事实，但无论是在书中还是在文章中，他们都找不到这种关系。 因此，尽管他们的网站上已要求不要在这种情况下打扰他，但他们还是决定趁机联系陶。
帕克说：“令我们惊讶的是，他在两个小时后回答，并说他从未见过这样的东西。” 除此之外，在陶的回答中，有三个独立的证明这一身份的证据。
张西宁，彼得·丹顿和斯蒂芬·帕克的方程式公开一周半后，物理学家和陶（Park称其为“数学的消防水带”）在互联网上发表了一篇论文，报道了一个新公式。 现在，这项工作已经由《数学物理通讯》杂志的专家进行了评估。 在发表于《高能物理杂志》（Denton，Park和Zhang）上的另
一篇论文中，使用该公式简化了描述中微子行为的方程。
专家说，该公式可能有更多的应用方法，因为在大量任务中，需要计算特征向量和特征值。 俄亥俄州大学粒子物理学专家
约翰·比克姆说：“它的用途广泛。” “谁知道她可以打开什么门。”
数学家也有同样的想法。 耶鲁大学数学家
Van Wu表示：“这既令人惊讶又有趣。” “我不怀疑仅使用有关特征值的信息就可以计算特征向量。”
Vu和Tao在2009年证明了相似的身份（这就是Denton，Park和Zhang决定与Tao联络的原因），但是，新公式显然不遵循旧公式。 尽管今年5月在数学工作中偶然出现了类似的公式，但其作者并未将其与特征向量和特征值相关联。
从某种意义上说，物理学家提出了一个关于数个世纪以前的数学对象的新想法，这并不奇怪。 自从人们开始指望10个手指以来，自然就启发了数学研究。 Vu说：“要使数学蓬勃发展，它必须与自然联系起来。” “别无他法。”
转型技巧
特征向量和特征值之所以如此普遍，是因为它们表征线性变换：拉伸，压缩，旋转或以其他任何方式均等地更改同一对象的所有部分的操作。 这些转换由称为矩阵的数字矩形阵列表示。 一个矩阵将对象旋转90度； 另一个则将其上下翻转并将其减半。
将此矩阵应用于给定的对象将使其相对于平面镜像，并将其高度加倍。 矩阵的特征向量描述了除缩放外，对象不变的方向。 矩阵的特征值描述了对象沿着这些特征向量缩放的程度。
特征向量A平行于垂直轴。 其特征值是2，因为对象的高度加倍。
特征向量B在反射平面中。 它的特征值是1，因为对象不会随其变化。
特征向量C垂直于反射平面。 其特征值为-1，表示相对于平面的反射。
通过删除矩阵的行和列，可以创建较小的矩阵。 它们的特征值以及原始矩阵的特征值可用于计算原始矩阵的特征向量。矩阵通过更改对象的“向量”（指向对象的每个物理位置的数学箭头）来实现此目的。 矩阵的特征向量是在应用矩阵后继续指向与以前相同方向的那些向量。 假设我们采用一个矩阵，该矩阵将对象绕x轴旋转90度：特征向量沿x轴定向，因为当所有其他点绕它们旋转时，该轴上的点不会旋转。
类似的矩阵可以使对象绕x轴旋转并压缩两次。 矩阵将对象的特征向量压缩或拉伸的程度，相应的特征值描述-在这种情况下为1/2（如果特征向量不变，其特征值为1）。
陶ence特征向量和特征值是独立的，通常必须从矩阵本身的行和列开始分别计算它们。 学生学习如何针对简单矩阵进行此操作。 但是新公式与现有方法不同。 “这种身份的有趣之处在于，您无需知道矩阵中包含的任何值即可计算某些东西，”陶说。
同一性应用于执行特征向量（与虚数相反）的真实变换的
Hermitian矩阵 ，因此适用于现实中发生的情况。 该公式根据此矩阵及其“较小矩阵”的特征值来表示埃尔米特矩阵的每个特征向量，该较小矩阵是通过从原始矩阵中删除行和列而获得的。
陶说，回想起来，这个公式似乎是合理的，因为次矩阵的特征值本身就编码了隐藏的信息。 但是，“例如，我个人从未想过这种事情。”
他说，与任务无关的工具很少出现在数学中。 但是，他认为特征向量和特征值的互连必不可少。 他说：“真是太美了，我确定该公式会在不久的将来找到应用。” “到目前为止，我们对她只有一种用途。”
狼人粒子
这种应用与中微子有关：中微子是已知基础粒子中最奇怪，研究最少和最秘密的。 每秒有数万亿个这样的粒子通过人体，但是由于它们实际上没有显示出它们的存在，因此它们的许多特性仍然未知。
有趣的是，该理论声称，正是中微子和反中微子的行为差异导致
宇宙中的物质超过反物质 。 如果两个对立面在“大爆炸”之后以相等的数量出现，它们将相互消灭，除了光，太空中将什么也没有留下。 中微子与反中微子之间的差异可能导致物质的严重过量。 约克大学和费米实验室的物理学家
黛博拉·哈里斯 （
Deborah Harris）说：“如果它们的行为有所不同，它将使我们对宇宙为何充满物质有所了解。”
邓波研究了
DUNE实验（深地下中微子实验，深地下中微子）。实验）以衡量此类差异。
该实验将测量从伊利诺伊州费米实验室向距离南达科他州的源头1300公里的地下探测器发出的中微子的特征，该实验利用了三种不同类型的中微子的事实：电子，介子和tau。 但是，每种类型都是量子力学混合物，中微子会振荡，随时随地改变其类型。 当中微子从费米实验室传播时，它们的混合物发生变化，因此介子中微子可以变成电子或tau中微子。
这些振荡由极其复杂的3x3矩阵描述。 基于特征向量和特征值，物理学家可以计算出一个表达式，该表达式描述介子中微子到达南达科他州时将变成电子中微子的可能性。 他们还计算出介子中微子成为电子反中微子的可能性。
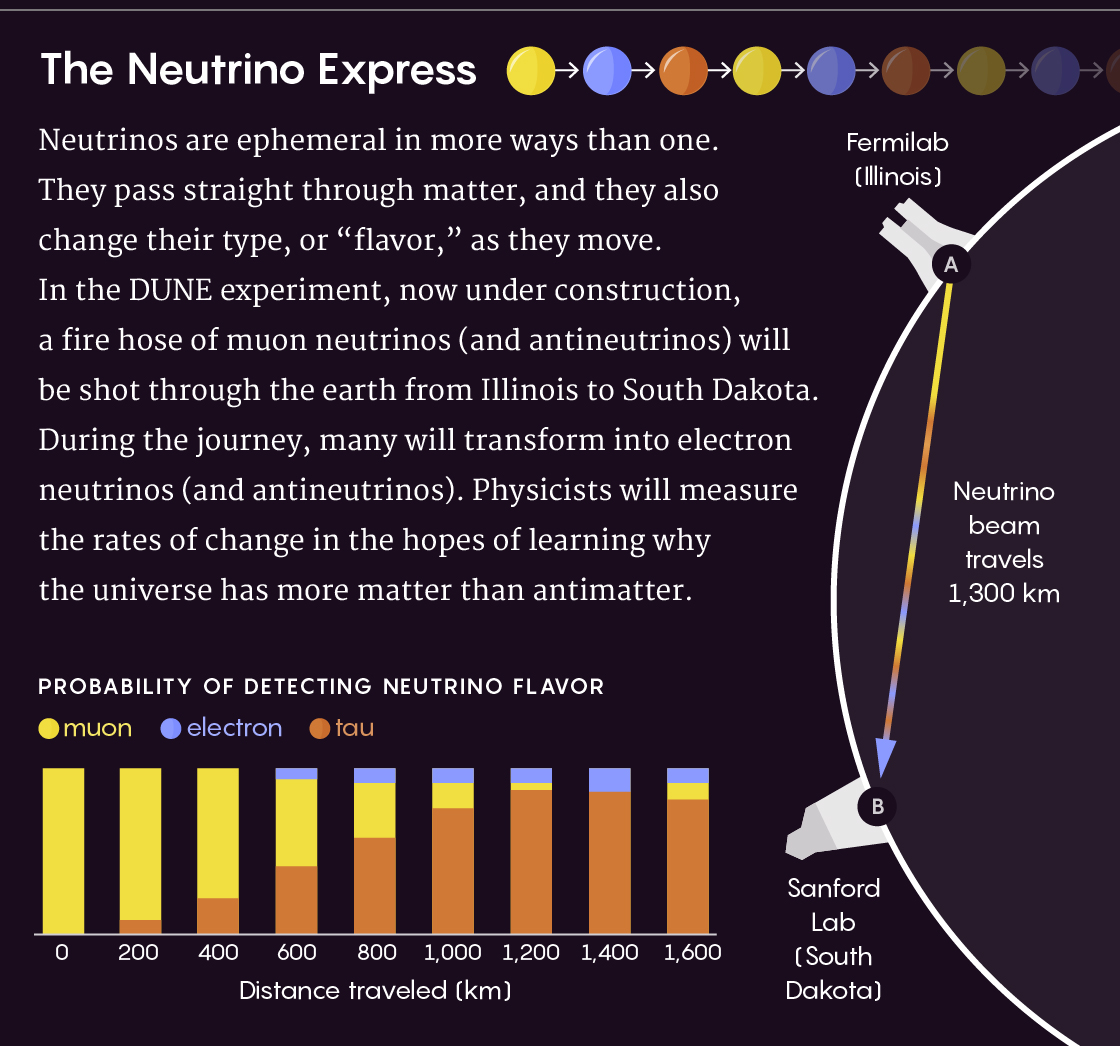中微子的短暂颗粒不仅会穿过物质，而且还会动态改变其类型。 在DUNE实验中，将发射中微子束，其中的许多中微束会在从源到目标的途中改变其类型。 这些变化将由物理学家来衡量。
该图显示了根据各种中微子的行进距离（以千米为单位）检测到中微子的概率。 黄色-介子色，蓝色-电子色，棕色-tau。这些表达式包含未知数：“
违反CP不变性的阶段”，它表明中微子和反中微子振荡的定律是如何彼此不同的。 通过测量和比较实际的振荡比，使用DUNE的科学家可以计算出未知数。 如果扰动阶段足够大，这将有助于解释为什么宇宙充满了物质。
似乎这些困难还不够，一个奇怪的效应使中微子矩阵更加复杂，而这种先决条件是物理学家林肯·沃尔芬斯坦于1978年首次
发现的 。 中微子很少以通常的意义与物质发生相互作用，但是德军总部发现，它们穿过物质的通道与空白空间不同，仍然改变了它们的传播方式。 有时穿透物质的中微子会与原子中的电子相互作用，从而实质上改变原子的位置：电子中微子会转变为电子，反之亦然。
这样的替代将新术语引入矩阵，影响电子中微子，这大大简化了数学。 正是
Mikheev – Smirnov – Wolfenstein的这种影响（由1985年苏联物理学家Stanislav Mikheev和Alexey Smirnov预测并在理论上进行了研究，基于在Wolfenstein中恒定密度的介质中中微子振荡的情况）促使Park，Zhang和Denton找到简化计算的方法。
用于计算特征值的表达式比用于特征向量的表达式更简单，因此Park，Zhang和Denton以此为起点。 在此之前，他们开发了一种新的特征值近似计算方法。 基于此，他们注意到以前工作中特征向量的长表达式等于这些特征值的组合。 将所有这些放在一起，“您可以轻松，快速地计算出物质中的中微子振荡”。
关于他们如何看待公式所遵循的模式，物理学家并不完全确定。 帕克说，他们只是注意到该模式的个别表现并对其进行了概括。 他还承认自己擅长解决难题。 他是另一个
重要规律的合著者，该
规律于1986年发现，它促进了粒子物理学领域的计算，并且至今仍在激发科学家新发现。
然而，中微子的奇怪行为可能导致与矩阵有关的新思想出现，这一事实震惊了很多人。 帕克说：“人们解决线性代数的时间非常非常长。” “我仍在等待某人向我发送一封电子邮件，上面写着：如果您查看
柯西的这项鲜为人知的作品，那么在第三附录的注释中就有这个公式。”
细微差异
实际上，已经知道了一个类似的公式，但是没有人注意到它，因为它被掩盖了。
9月，陶涛收到了另一封意外的电子邮件，这次是来自澳大利亚墨尔本大学数学研究生张继元的。 张指出，在陶和三位物理学家的作品出现之前，他在五月与策展人
彼得·弗雷斯特 （
Peter Forester）撰写的
作品中存在一个等效的公式。 Zhang和Forrester从事纯数学领域（随机矩阵理论）的研究。 他们应用了此公式，并探索了与陶先生及其同事在1999年解决问题相关的问题。
Forester向我们解释说，该公式在2001年的
工作中首次以另一种形式出现，该词由现任伊利诺伊大学香槟分校分校的数学家
Julia Baryshnikova撰写，Forester和Zhang的工作基于该公式。 但是这些数学家不是将特征的对象描述为特征向量，而是将其作为计算在解决问题过程中出现的某些次要矩阵的特征值所必需的术语。
佛雷斯特称张在他的工作中的公式与陶和三位物理学家所用的公式“相同”。 陶称这些公式“几乎完全相同”，它们以与兔子/鸭错觉的两个侧面相同的方式相互指代。 他说：“有些人在寻找兔子，其他人只在寻找鸭子。”
丹顿在一封电子邮件中写道，以前存在的公式“接近我们的结果，但并不完美”。 他补充说：“鉴于本征向量在许多问题上的重要性，我们仍然认为我们的结果与其他问题相去甚远，因此认为它是新的。”
在几个世纪后的一个夏天，在这个地区出现这种突然的兴奋也许并不奇怪。 陶说：“有许多同时发现数学的例子。” -结果悬而未决。 人们只是在正确的地方开始寻找他们。”