我曾经写过
一篇文章 ,其中描述了一个简单的数学模型,描述了神经网络的演化及其在具有2为底和黄金比例的数字系统中加数字的能力的选择,结果证明黄金比例效果更好。 因此,我的初次体验非常糟糕,因为我没有考虑到与以下事实有关的许多重要细微差别:对于神经元不应该考虑错误,而对于一些信息,所以我决定改进我的实验,并介绍更多调整。
- 我决定在具有从1.2到2均匀分布的底数而不是两个以前已知的底数的数字系统中检查15对(训练样本)和1000(测试样本)向量的100对样本。
- 我还不仅从距底数与黄金比率的距离进行了线性回归,还从距基数本身,向量中的坐标数和响应向量中的坐标平均值进行了线性回归,以考虑误差对基准的非线性依赖性。
- 我还通过Kolmogorov-Smirnov准则ANOV检查了一些样本的正态性,但是这些准则表明样本极有可能偏离高斯,因此我决定进行加权线性回归,而不是通常的线性回归。 但是,ANOVA尽管显示F值比以前小一些(在700-800范围内,而不是800-900范围内),但结果仍具有统计学上的显着性,这意味着应该进行更多的测试。 在进行这些测试时,我绘制了回归残基和正常QQ分布密度的直方图-这些残基的分布函数图。
这两个图是:
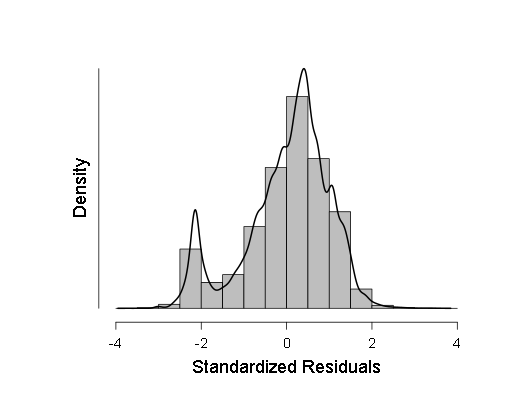
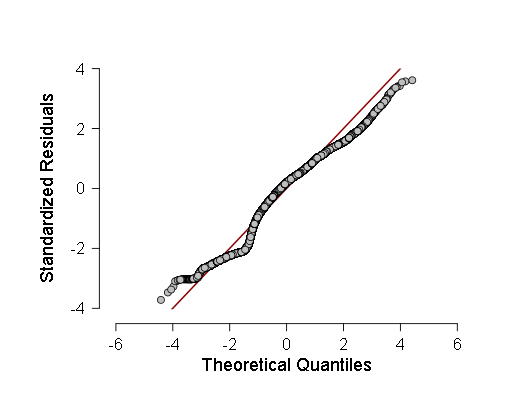
可以看出,尽管在残差分布中与正态分布的偏差在统计上是显着的(并且在左侧,即使在直方图上也可以看到很小的第二模式),但实际上它与高斯非常接近,因此,可以(谨慎和较大的置信区间)依靠此线性回归。
现在介绍如何生成样本以测试它们上的神经网络。
这是头文件代码: #include <stdio.h> #include <stdlib.h> #include <math.h> int main(void); void calculus(double a, double x, bool *t, int n);// x a t n . void calculus(double a, double x, bool *t, int n) { int i,m,l; double b,y; b=0; m=0; l=0; b=1; int k; k=0; i=0; y=0; y=x; // t . for (i=0;i<n;i++) { (*(t+i))=false; } k=((int) (log((double)2))/(log(a)))+1;// , . while ((l<=k-1)&&(m<nk-1)) // x a ( ), { m=0; if (y>1) { b=1; l=0; while ((b*a<y)&&(l<=k-1)) { b=b*a; l++; } if (b<y) { y=yb; (*(t+kl))=true; } } else { b=1; m=0; while ((b>y)&&(m<nk-1)) { b=b/a; m++; } if ((b<y)||(m<nk-1)) { y=yb; (*(t+k+m))=true; } } } return; }
接下来,让我们谈谈我如何进行加权线性回归。 为此,我只计算了神经网络结果的标准偏差,然后将其划分为单位。
这是我用来执行此程序的源代码: #include <stdio.h> #include <stdlib.h> #include <math.h> int main(void) { int i; FILE *input,*output; while (fopen("input.txt","r")==NULL) i=0; input = fopen("input.txt","r");// . double mu,sigma,*x; mu=0; sigma=0; while (malloc(1000*sizeof(double))==NULL) i=0; x = (double *) malloc(sizeof(double)*1000); fscanf(input,"%lf",&mu); mu=0; for (i=0;i<1000;i++) { fscanf(input,"%lf",x+i); } for (i=0;i<1000;i++) { mu = mu+(*(x+i)); } mu = mu/1000; while (fopen("WLS.txt","w") == NULL) i=0; output = fopen("WLS.txt","w"); for (i=0;i<1000;i++) { sigma = sigma + (mu - (*(x+i)))*(mu - (*(x+i))); } sigma = sigma/1000; sigma = sqrt(sigma); sigma = 1/sigma; fprintf(output,"%10.9lf\n",sigma); fclose(input); fclose(output); free(x); return 0; };
接下来,我将所得的权重添加到表中,在表中,我将减少程序所得的所有数据以及变量的值以计算回归,然后在JASP中对其进行计算。 结果如下:
结果
线性回归
接下来,我有一个标准化回归残基分布密度的直方图:

以及标准回归残差的正态分位数图:

然后,我将在其过程中获得的回归系数的平均值应用于变量,并进行了统计分析,以使用费马引理,贝叶斯定理和拉格朗日定理从数字系统的基数(与这些变量有多少关系)中找到误差函数的最可能最小值。如下:
事实是样本中数字系统的基数分布显然是均匀的,因此,如果区间(1,2; 2)中的某个基数是均方误差的最小值,那么根据费马引理,它将具有零导数,则值的概率密度为该函数将是无限的。
现在介绍如何应用贝叶斯定理。 我计算了beta分布的置信区间(这是在n个“成功”和m个“失败”且概率密度为条件下,实验中“成功”的概率分布
)计算得出的误差的分布函数的值(这是随机变量不大于自变量的概率),源于以下事实:如果随机变量不大于自变量,则为``成功'',如果大于,则为``失败''。 然后,使用贝叶斯定理,我们应用计算出的误差的分布函数的beta分布,并计算其在每个计算出的误差中的[分布函数]置信区间为99%。
我们传递给拉格朗日定理。 拉格朗日定理指出,如果函数f(x)在区间[a; b]上是连续可微的,那么至少在该区间的一点上,它的导数等于
。 我如何应用该定理:事实是概率密度是分布函数的导数,因此我取了最大值,它恰好需要从最小误差到剩余误差的一定间隔。 然后,我使用以下公式计算这些值在98%(使用Bonferroni校正)中的置信区间:
其中F1是分布函数的置信区间的左端,F2是右边,x_i,x_1是作为分布函数的参数计算出的误差。 接下来,程序搜索具有最大左端和最大右端的间隔(以使该间隔中的值是最大值),然后在与该间隔中计算出的误差相对应的基数中查找最大值和最小值。 这些最大值和最小值是错误函数自下而上的参数,介于函数本身的最小值之间,概率为98%。
这是头文件代码: #include <stdio.h> #include <stdlib.h> #include <math.h> int main(void); double Bayesian(int n, int m, double x);// - n "" m "", " " " " , : double Bayesian(int n, int m, double x) { double c; c=(double) 1; int i; i=0; for (i=1;i<=m;i++) { c = c*((double) (n+i)/i); } for (i=0;i<n;i++) { c = c*x; } for (i=0;i<m;i++) { c = c*(1-x); } c=(double) c*(n+m+1); return c; } double Bayesian_int(int n, int m, double x);// - ( ): double Bayesian_int(int n, int m, double x) { double c; int i; c=(double) 0; i=0; for (i=0;i<=m;i++) { c = c+Bayesian(n+i+1,mi,x); } c = (double) c/(n+m+2); return c; } // : void Bayesian_99CI(int n, int m, double &x1, double &x2, double &mu); void Bayesian_99CI(int n, int m, double &x1, double &x2, double &mu) { double y,y1,y2; y=(double) n/(n+m); int i; for (i=0;i<1000;i++) { y = y - (Bayesian_int(n,m,y)-0.5)/Bayesian(n,m,y); } mu = y; y=(double) n/(n+m); for (i=0;i<1000;i++) { y = y - (Bayesian_int(n,m,y)-0.995)/Bayesian(n,m,y); } x2=y; y=(double) n/(n+m); for (i=0;i<1000;i++) { y = y - (Bayesian_int(n,m,y)-0.005)/Bayesian(n,m,y); } x1=y; }
这是该程序工作的结果,当我给她数字系统的基础和回归结果时:
x (- [1.501815; 1.663988] y (- [0.815782; 0.816937]
(在这种情况下,“(-”只是集合论中符号“属于”的一种表示法,方括号表示间隔。)
因此,在我看来,就传输信息中的错误而言,数字系统的最佳基础是从1.501815到1.663988,即黄金分割率完全落入其中。 没错,我在计算最小值时做出了一个假设,而在不同数字系统中计算了信息量时又做了一个假设:首先,我假设来自基数的误差函数是可连续微分的;其次,均匀分布数的概率为1, 2到2在特定的数字中将具有数字1,在小数点后的某个数字之后将大致相同。
如果我做的事情完全错误,或者完全是错误的,我很乐意提出批评和建议。 我希望这种尝试会更加成功。
UPD 我对文章进行了两次编辑,以澄清“纯粹科学”部分中的某些地方,并格式化代码。
UPD2。 在与了解生物信息学的人(IPPI RAS的FBB MSU研究生课程的毕业生)进行咨询之后,决定将“大脑”一词替换为“神经网络”,因为它们之间存在很大差异。