亚历山大·库什内罗夫（Alexander Kushnerov）
12/18/2019
即使是经验丰富的工程师，有时也会发现很难对电路进行布线，从而使走线（或电线）不会干扰其正常运行。 在第一近似中，将导线连接到每个节点的节点的布局和数量以及分支之后导线的长度影响布线的质量。 如果我们将电线的长度视为延迟，则异步数字电路的正确操作可能不取决于某些电线的延迟。 将来，我们会将这种电线称为安全的，并将这种电线的分支称为完全安全（FGP）。 在本文中，我们将展示由十二个晶体管组成的通用电路如何使某些分支完全安全。
考虑图1所示的所谓“蝴蝶”方案[1]，[2]。 1.该电路产生不相交的脉冲p和q，可用于控制功率晶体管。 图中的缓冲区 1表示安全电线。 假定所有其他导线的延迟为零。 脉冲之间的间隔由缓冲区wy和wz的延迟设置。 将来，我们将不再使用缓冲区来指示元素的延迟。 本文所有电路中的电线和分支在Workcraft [3]中进行了安全性（输出持久性）测试。 通过解决CSC冲突，从电路中获得了信号转换图（STG）。 这些插图显示了简化的STG，其中已删除了缓冲信号。 图中的时序图（TD） 根据相应的STG来构造图1中的示例。
图 1.“蝴蝶”电路，其STG和TD（假设导线中的延迟为零）。从理论[1]，[2]中可以知道，RS触发器的电路对交叉耦合中的导线延迟很敏感。 这就是为什么图1中的交叉链接中的缓冲区是 1失踪。 因此，两个触发元件必须彼此保持最小距离。 如果很难做到这一点，则可以用一个有反馈的复杂元素替换两个元素。 例如，蝶形电路中的元素x和xb可以如图所示进行替换。 2.另外，我们在复杂元素的输出处获得FGP。
图 2.图1所示电路的一种变型。 图1及其STG是在导线的延迟为零的假设下得出的。图中方案的实现 1和图。 2分别需要16和20个晶体管。 另外，图中的图。 2的速度较慢，因为反相器wb1，wb2和元件2 OR-AND内部的反相器必须每个周期切换两次。 性能低下通常是FGP的代价。 但是，此规则也有例外。 例如，在图 图3示出了具有两个FGP的异步计数触发器（AST）[4]的方案。
图 3.在导线延迟为零的假设下，AST及其STG。图中电路的缺点 3是大量导线，并且大多数导线相交。 这会使布局复杂化，尤其是在带走线的层数有限或被其他化合物占据的情况下。 因此，您需要在导线数量，晶体管数量和FGP数量之间寻找折衷方案。 具有一个FGP的这种折衷方案的一个示例是图1中所示的AST。 4.这是对[5]电路的小修改。 请注意，如图所示。 2，使用混合基准。 为了在没有指示器的情况下实现此AST（wi2，wi4和g5的XOR），需要26个晶体管。 仅比图1中的AST多两个晶体管。 3。
图 4.当线路中的延迟为零时，请妥协AST及其STG。请注意，图2中所有带有反馈的元素。 2和图。 4是广义C元素（gC）的特例。 给出为[6]：
y=S（x）+y\上线R（x） 在哪里
S（x） 和
R（x） 安装和重置功能是否满足条件
S（x）R（x）=0 。 gC元素的特殊情况也是NCL元素，它们在数据处理方案中使用。 注意，最大的NCL元件具有四个输入，并在28个晶体管上实现[7]。 这可以通过以下事实来解释，即，随着晶体管数量的增加，导线变得相对较长，并且导线中的延迟开始影响元件的操作。
考虑图1所示的晶体管电路。 5.它实现了五个变量[8]，[9]的功能
f（x）=x1x3+x2x4+x5（x1x4+x2x3） 。 表1显示了SDNF和SKNF函数
f（x） 及其双重功能
φ（x）=\上线f（\上线x） 。 从该表可以明显看出，通过互换
x2 和
x3 在
f（x） 我们得到
φ（x） 反之亦然。 万一
x2=x3=y ，我们得到了自我对偶功能
f（x，y）=\上线f（ overlinex， overliney）=x1x4x5+y（x1+x4+x5） 。
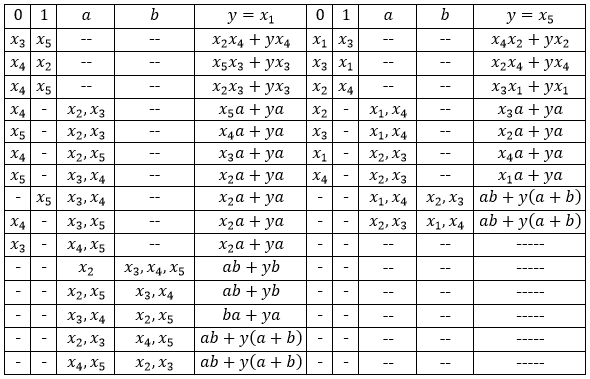
图 5.实现五个变量功能的方案。表1.图中电路的逻辑功能形式 5，
注意
x2=x3=y 意味着必须同时切换相应的四个晶体管。 即使分支y之后的导线具有相同的延迟，这也是不够的，因为晶体管的开关力矩由其栅极电压决定。 从这个角度出发，对图1中的电路进行分析。 [10]中制作了5个。 但是，由于仅考虑了两输入C元素的实现，因此该分析并不完整。 要进行全面分析，您必须首先找到用于组合输入的所有选项，或更正式地讲，可以从中获取较少数量的变量的所有函数。
f（x） 。 这种搜索以某种简化的形式执行，其结果显示在附录中。 大多数功能都有几种变体。 从他们那里，有必要选择那些提供无竞争方案的方案[11]。 表2列出了所获得的所有功能，每种功能的变体数量以及附录中相应表格的数量。带星号的数字表示双重功能。
表2.由图1中的电路实现的gC元素 5，
函数2和2 *，5和5 *，7和7 *是对偶的，可以通过互换a和c从函数4 *获得函数4。 请注意，除了功能6 *外，所有其他功能均为阈值。 这可以通过以下事实来解释：
f（x） 是等渗的（正整数），并且对于四个或更少的变量，等渗函数与伪阈值重合[12]。 本文中的功能1 *，3 *和6 *具有哪些选项的问题仍然悬而未决。
以功能2和2 *的情况为例。 根据其中一个选项（附录中的表P3）
x1=x4=a 和
x2=x3=b 。 让路
y 从入口断开
x5 并从逆变器输入中去除信号。 这使您可以构建如图1所示的细胞输送器分配器[13]。 6.该单元中的元素是不同的，但是由于合并了输入，因此它们都实现相同的自对偶功能。 注意，图1中的电路中的交联元件是相同的。 图1中， 3和图。 6是完善实施的基础结构的特例[2]。 因此，必须有规则将基本设计电路转换为gC元件电路，反之亦然。
图 6.细胞输送器分配器。从技术角度来看，应将晶体管“串接到”多晶硅总线上。 图1中的电路的这种实现。 在[14]中给出5。 要设置初始状态，可以使用p-MOS和n-MOS晶体管，它们在反相器中与晶体管形成分压器。 借助某些STG转换，可以提高电路的抗干扰性[15]。
致谢
作者非常感谢Svetlana Frolova（OmSU）扫描本文[1]，也感谢Sergey Bystrov的启发。
应用程式
MuPAD用于获得本节中介绍的结果。 让输出y仅连接到输入之一。 表A1显示了这种情况
S（x）R（x）≠0 。 获得其功能
S（x）R（x）=0 ，您可以合并一些变量或为它们分配常量。 表A2中给出了组合两个变量的情况下的功能。 其他选项不给
S（x）R（x）=0 。 由于表A1中的前四个函数与变量的排列重合，因此我们将仅考虑第一个和第五个。 案例
y=y（∀） 和
y=（∀）+y 没意思，因为在第一种情况下，我们只能重置gC元素，但无法安装，在第二种情况下，反之亦然。 使用变量进行操作可以从表P1获得四个和三个变量的功能，分别在表P3和表P4中给出。
表A1。 五个变量的功能。
表A2。 四个变量的功能。
表P3。 从表A1获得的四个变量的功能。
表A4。 从表A1获得的三个变量的功能。
文学作品
[1] V. I. Varshavsky，M。A. Kishinev，A。R. Taubin和B. S. Zirlin，“异步逻辑电路分析。 二。 工作状态的可达性和电线延迟的影响。 苏联科学院。 技术控制论，没有。 4页。 1982年第84-97页。
[2] Varshavsky，V. I.（ed。），计算机和离散系统中异步过程的自动控制，Nauka，1986年。
[3]
workcraft.org 。
[4] RC Todd，“逻辑系统”。 9月28日专利US3609569 1971年。
[5] EA Vittoz，“分频逻辑结构”。 专利US3829714，8月13日。 1974年。
[6] J. Cortadella，M。Kishinevsky，A。Kondratyev，L。Lavagno和A. Yakovlev，异步控制器和接口的逻辑综合，Springer，2002年。
[7] A. Kondratyev，“具有完成检测功能的多轨异步流及其设计方法和系统。” 2月25日，专利US6526542。 2003。
[8] JJ Gibson，“采用场效应晶体管的逻辑电路”。 4月15日专利US3439185 1969年。
[9] R. Miller，开关电路理论。 第I卷，《组合方案》，《科学》，1970年。
[10] K. van Berkel，“当心等时叉”，《综合》，第一卷。 13号 2，第 第103-128页，1992年。
[11] P. Kudva，G。Gopalakrishnan，H。Jacobson和SM Nowick，“多输入变化下无危害的定制CMOS复杂门网络的合成”，设计自动化会议，1996年。
[12] GW Fagerlin，列举五个变量的伪可分函数。 理学硕士 论文，伊利诺伊大学，1968年。
[13] V. I. Varshavsky，A。Yu。Kondratiev，N。M. Kravchenko和B. S. Tsirlin，“异步发行人”。 1990年7月10日获得专利SU1598142。
[14] SW Cheng，IEEE Conf。中的“ H-tree CMOS逻辑电路”。 电子，电路与系统专业，2008年。
[15] A. Taubin，A。Kondratyev，J。Cortadella和L. Lavagno，“行为转换以提高异步规范中的抗扰度”，在IEEE Symp中。 在异步上。 电路与系统，1999年。