关于奇怪的问题（再次）和晶体管的选择

找到一切的理由，您将了解很多。

我的一位年轻同事（以下称为MMK）设计的设备中出现了另一个谜。 该设备专为18650系列电池的传入控制而设计（不，Ilon Mask可以安然入睡，我们公司不会生产电动汽车，这是用于其他产品的），并在相当著名的BQ29700芯片上实现，该芯片与许多类似的电池控制器不同，只有两个有关管理密钥和控制电流的单独结论（“我的朋友，关于悬挂装置，请不要忘记”）。 该方案完全按照制造商的建议实施（请参阅KDPV），完全没有问题，但是……有。



接下来是小型工程调查的经验，然后是琐碎的（可能是无聊的）道德。

在继续描述问题之前，让我们先讨论一下实际推荐的方案。 首先，请注意琴键在下肩（中性线）而不是上琴键的事实。 为什么这样 答案-因为微电路是按这种方式设计的-不被接受，因为它提出了一个问题-为什么采用这种方式设计。


下一个问题是为什么要有两个晶体管：每个人都知道答案-因为我们需要一个双向开关，而内置二极管的存在使得不可能在单个晶体管上实现。

但是下一个问题更有趣-为什么晶体管通过喷嘴相互连接，看来您可以将它们与另一端连接（因为它们被称为自己决定）。


好了，现在关于问题本身了-组装好的设备无法正常工作。 外部症状和既定事实：

1. 安装测试电池（BAT）后，电压不会流到外部端子（或者不会流到较低的负极）。
2. 晶体管T1（充电键）导通，晶体管T2在栅极（输出Dout）处截止为低电平。
3. 在+和-端子（充电模拟器）上施加外部4.2V电压后，两个晶体管均导通，而在去除外部电压后，它们保持导通状态并可以测试电池。
4. 从插槽中取出电池后，请转到步骤1。

通常，似乎在安装电池后，微电路认为有必要对其进行充电（至少以少量充电），然后才准备使其用作电源。 好吧，首先，这是一个相当奇怪的行为，其次，为什么在文档中没有对此进行描述，因此该假设看起来令人怀疑。 MMK采取了一种久经考验的现代方法来查找故障原因-在Internet和e2e论坛上进行搜索时，发现了一个类似情况的问题，TI大师给出了一个奇怪的答案（在我看来），该芯片旨在用于焊接电池，并且插件将不被接受。 毕竟，还有些垃圾被插入了焊接电池，所以我们将使用旧方法寻找原因-实验（测量也是实验）并了解其结果

我们走得更远-电池上的电压是正常的，设备的框图中没有触发器（尽管现代框图，如描述一样，是一首单独且令人沮丧的歌曲的主题），但是其中一个键是闭合的，因此电流传感器起作用了，没有别的了。 同时，在框图中有一个逻辑节点，描述涉及触发器（但在稍有不同的方面）和一个内部计数器。 进一步认为，当放电过程中发生过电流情况时，电路会进入缺陷模式，并在除去负载或施加充电电压后从缺陷模式返回正常模式，这与我们的情况非常相似。

为了进行测试，我们将电阻器R1的下端连接到Vss引脚（这很重要，MMK悬空悬空，在这种情况下还不够），并且...效果消失了。插入电池后，两个晶体管都打开了，输出电压被提供给外部端子。

Pnp：断开电源但仍未断开电源仍会产生一些细微的影响，我没有将它们考虑在内。

因此，电流限制仍然有效，但令人恐惧-现在，当插入电池时，我们已断开负载。 接下来，我们连接和断开一个小的负载，电流流动，这是很正常的，没有截止。

这意味着，或者在插入电池时，电流流过比允许电流大得多的电流，或者电路错误地决定超过电流。 您可以连接示波器并查看，但是最好考虑一下，因为您仍然必须考虑一下。

立即做出决定-从连续连接到插入电池的过程有什么区别-弹跳的存在。 如果我们考虑到电池上的电压是通过滤波器R2C1提供给微电路的，而+端上的电压是直接通过电阻R1来提供的，那么当输入BAT仍可工作且输入V-已经为零时，可能会出现这种情况。 然后，微电路确定按键上的所有电压均已下降，然后超过了电流，并且放电按键被关闭-一切似乎合乎逻辑。

同时，应注意的是，由于微电路内部存在延迟，因此过电流检测器的操作应较长，最长10 ​​ms，并且电源滤波器的时间常数330 * 0.1 * 10 **-6 = 33μs是矛盾的。 但这是与电容器充电相关的时间常数，但不会通过电阻器放电（因为当电池在电路板的第二接触垫上嘎嘎作响时，不会为零，而是断裂），而是通过微电路。 然后，在消耗电流为1 mA的情况下，电容器两端的电压从4.2 V将在0.1 * 10-6 * 1.6 / 1 * 10 **-3 = 0.16 ms内降至2.8 V，而在30 ms内已经有5.5μA的电流就足够了决定过电流。

这种行为还有另一个可能的原因，例如可以通过简单地向微电路加电来重置（安装）触发器（不，这个假设似乎被切换电阻器驳斥了，尽管并非一切都如此明显），这将导致相同的结果。 没有设备图，框图不够丰富，因此最终选择取决于个人喜好。

通常，确定上述微电路行为的原因（通常不完全，所提出的机制只是可能的一种，尽管似乎是合理的，但我们唯一可以确定的是它与电流控制有关），没有发现任何缺陷，很奇怪论坛上的答案不再是一个奇怪的问题（尽管它并没有变得更加有益）。 如何精确地处理这种现象-有很多方法，一种不差一种，MMK选择了最简单的一种-将电阻器的下端留在新的位置并关闭电流控制。 如果我们确定已经校准了负载，并且没有人会在不应该使用的地方安装镊子，则该解决方案是可以接受的（但这在这里比较困难。但是，我们仍然没有受到使用镊子的“技术熟练的傻瓜”的保护，这是-缺少接地开关）。

现在是标题中所反映的Marleson芭蕾舞的第二部分。 我们修复了缺陷，插入电池并观察设备输出端的电压，连接4欧姆的标称负载，...其上的电压从4.2V急剧下降至2.0V，电池仍产生4.1V。 因此，在两个串联的晶体管上，2.1V的压降太大了，我们会明白的。

好吧，这里没有谜语，控制电压显然不够，这使我可以平稳地转到文章的第二部分。 首先，我们在晶体管上打开日期，然后在此处看到-在场效应晶体管的数据表中应该看到什么。

严格来说，我们应该至少看到两组两个参数：栅极-源极电压和源极电流，以及绝对任意点。 假设场效应晶体管的传递函数为

$$

$$是（微克）= Iso *（1-微克/乌格斯）** 2$$

，两个电压/电流对足以找到两个未知数。 我们写两个方程

$$

$$I1 =（Iso / Ugso ** 2）*（Ugso-Ugs1）** 2$$

和

$$

$$I2 =（Iso / Ugso ** 2）*（Ugso-Ugs2）** 2$$

，然后将第一个除以I2，得到

$$

$$（I1 / I2）* Ugso ** 2 / Iso =（Ugso-Ugs1）** 2 / I2$$

。 然后，在条件（I2 >> I1）&&（Ugso！= 0）下，我们得到的答案是Ugso = Ugs1的一半。

现在很明显，我们仍然在选择常识性常识点方面受到限制，并且它们中的第一个应该在晶体管的开口点附近，以使电流足够小。 通常，这是一个电流为250μA的点，对应于栅极电压的两个值-最小值和最大值（也有一个典型值，但几乎没有）。 但是，这两个含义到底意味着什么：

1.我们可以确保，当栅极处的电压小于或等于最小值时，我们将永远不会获得更明显的电流。

2.我们可以确保，当栅极处的电压大于或等于最大值时，我们将永远不会获得比所示电流小的电流（当然，只要电路的外部元件能够为其提供晶体管）。



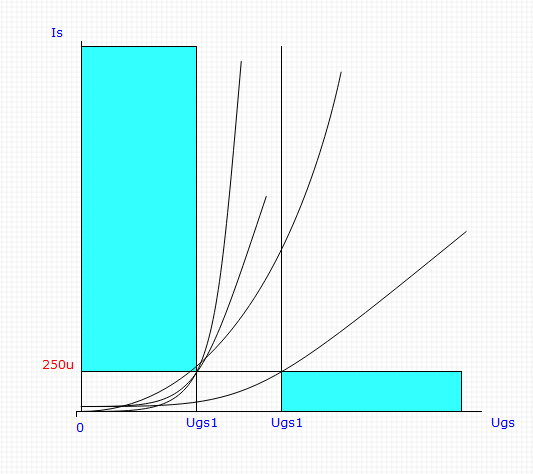
在上述两个条件之上，我们不能保证任何事情，请注意禁令规定的时间表。 它所有未填充的部分都是可能的传输特性区域。 特别是，对于在所示范围内的电流值的任何假设都是正确的，我用黑色表示了其中的一些。

所有关于常识的相同考虑，逻辑上选择一个具有较大电流的第二点，通常表示栅极处的最大电压，在该点处流过一定的较大电流，通常接近最大工作电流，再次注意公式2。那么我们可以计算出未知参数

$$

$$Iso = I2 * Ugso ** 2 /（Ugso-Ugs2）** 2$$

我们可以为漏极上任何电压下的电流写一个表达式

$$

$$是（Ugs）= I2 * Ugs1 ** 2 /（Ugs1-Ugs2）*（Ugs1-Ugs）** 2 / Ugs1 ** 2$$

简化，我们得到

$$

$$是（微克）= I2 *（微克1-微克）** 2 /（微克1-微克2）** 2$$

很容易看出，Ug€[Ugs1 ... Ugs2]的最后一个表达式随Ugs1的增加而减小，因此，为了计算在一定栅极电压下的最小（保证的）漏极电流，我们应取Ugs1的最大值。

细心的读者会放弃-如果不难，那么证明在哪里，公式中的参数同时出现在分子和分母中，因此您的陈述并不明显-绝对正确。 我们能回答他什么：

1. 取一个特定的晶体管，计算边缘和中间的值，并指出最小的精确位置。 该方法是一般的，因为它不能证明没有特定的内部点可以使计算得出的值甚至更少。
2. 绘制不同阈值的漏极电流图，并提供视觉验证。 该方法稍好一些，但它仅是说明性的，还需要进行其他分析，因此可以轻松地立即转到方法3。
   
   
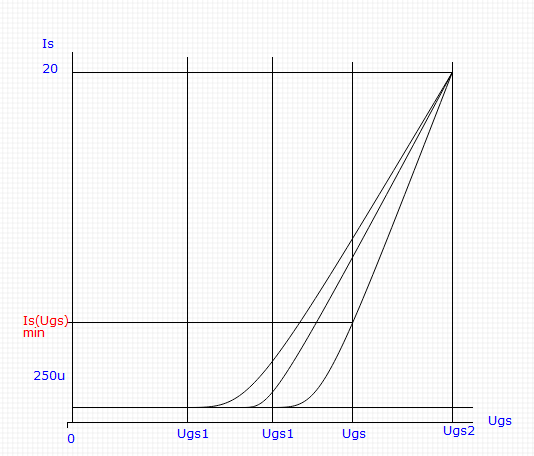
3. 为了分析表达式，我们针对变量Ugs1对其进行了派生，经过一系列简化后得到

   $$

   $$是'（Ugs1）= 2 * I2 *（Ugs1-Ugs）*（Ugs-Ugs2）/（Ugs1-Ugs2）** 3$$
   。 我们看到五个因素（常数除外），每个因素对我们的条件都是负的，这意味着导数为负，并且函数在范围的右边界达到最小值，等等。

考虑以下特定示例，基于这种电池放电的截止电压为2.6V，即在栅极上达到给定电压的事实，晶体管必须提供1C = 1A的放电电流。

所选的MMK晶体管是2.0V-4.0V栅极的初始开路电压，因此，计算2.6V的保证电流根本没有任何意义，它可以取任何值，包括零，无需说明。 细心的读者会问一个问题-毕竟，流过晶体管的电流确实流过了，知道负载后，就可以计算出它的值了（它不是那么小，大约为0.5A）。 我会回答-我们有一个充满电的电池，电压为4.2V，我们有一个晶体管的阈值电压低于最大值，但这并非总是如此。 工程师必须依靠最坏的情况，而无权要求最好的。

选择另一个晶体管时要考虑到批评，但根据库存的主要标准：初始电压1.4V-2.6V，在2.6V时，我们得到的保证电流为250μA，这显然是不够的。 让我们尝试降低要求并提高到2.8V，然后考虑20A在4.5V下，我们得到I（2.8）= 20 *（2.8-2.6）** 2 /（2.8-4.5）** 2 = 20 * 0.2 ** 2 / 1.7 ** 2 = 0.22A，这还不够。 对于3.0V的计算显示了0.8A的电流值，只有在3.2V时才获得所需的1A。 当然，我们可以期望在2.0V的平均阈值，然后在2.6V时有1.12A的电流，一切都很好，但是，正如我上面所说，“希望”一词不应该包含在工程师的词汇中。

现在考虑TI推荐的SCD16406晶体管，其初始电压为1.4V-2.2V，并且具有相同的极限值。 然后我们在2.6 V时得到的保证电流等于20 *（2.6-2.2）** 2 /（2.2-4.5）** 2 = 0.6 A，这很奇怪，就是这样-截止电平为2.8 V，有了这个电压根据要求，1.36A意味着TI一切正常。 如果MMK更加注意阅读最终的技术文档（RTFMF），也将拥有它。 同时，我不得不指出，我认为该公司对选择晶体管以实现推荐电路中的密钥的问题没有给予足够的重视，尽管否则将不会有此职位，因此我们正在寻找所有方面的亮面（以及特征）。

最后，还有另一个问题-为什么在文档中它们给出了阈值电压的最小值，因为我们根本没有使用它来计算保证电流。 答案是确定保证不导通晶体管的阈值。 如果对通过断开的晶体管的250μA电流感到满意，则可以通过将栅极电压设置为等于下限阈值来接收该电流。 如果需要较小的电流，则应该对Io值进行类似的计算，并使用通用公式确定漏极电流变得非常小的栅极电压。

对于最后考虑的晶体管
Io = I2 ** U1 ** 2 /（U1-U2）** 2 = 20 * 1.4 ** 2 /（3.1）** 2 = 4.08A
然后值（1-U1 / U0）** 2与1的差异为0.00025 / 4.08〜0.5 * 10 **-5，我们取等于2 * 10 **-3的平方根，这意味着我们需要降低栅极上的电压2 * 10 **-3 * 1.4，即0.006V，这样晶体管漏极中的电流就完全停止了（由于晶体管的放大特性，该部分电流）。 一般规则如下-Ugs1（最小）-0.1V在绝大多数情况下足以完全关闭晶体管，尽管您仍然应该看一下该参数的测量模式，正如Winnie所说，“您可以期望猪提供一切”。

哦，是的，我向人们保证，这是道德。这是当然的：工程师与其他所有人的不同之处在于他用手思考，但是普通的（在大脑的帮助下）思考和关注细节在工程实践中同样重要。 是的，这是微不足道的，但还是如此。