也许很难将测地线穹顶称为不寻常或新颖的东西。 在本文中,我将大致讨论这些设计,它们的结构,并举例说明如何考虑该主题。 代码也将是。
我不会引用维基百科。 为什么选择圆顶作为我的家?
- 在相等的体积下,球体的表面积将小于任何其他形状的表面积。 这对运行过程中的材料消耗和能量消耗都有积极影响。
- 我喜欢球体的外观。
- 从某种意义上说,这是一个有趣的工程项目,甚至是挑战。 这是困难的,困难的,因此很有趣!
这些测地线总体上如何布置? 乍一看,这似乎是边缘的某种交织,很难抓住系统。 我们将尝试解决这个问题。
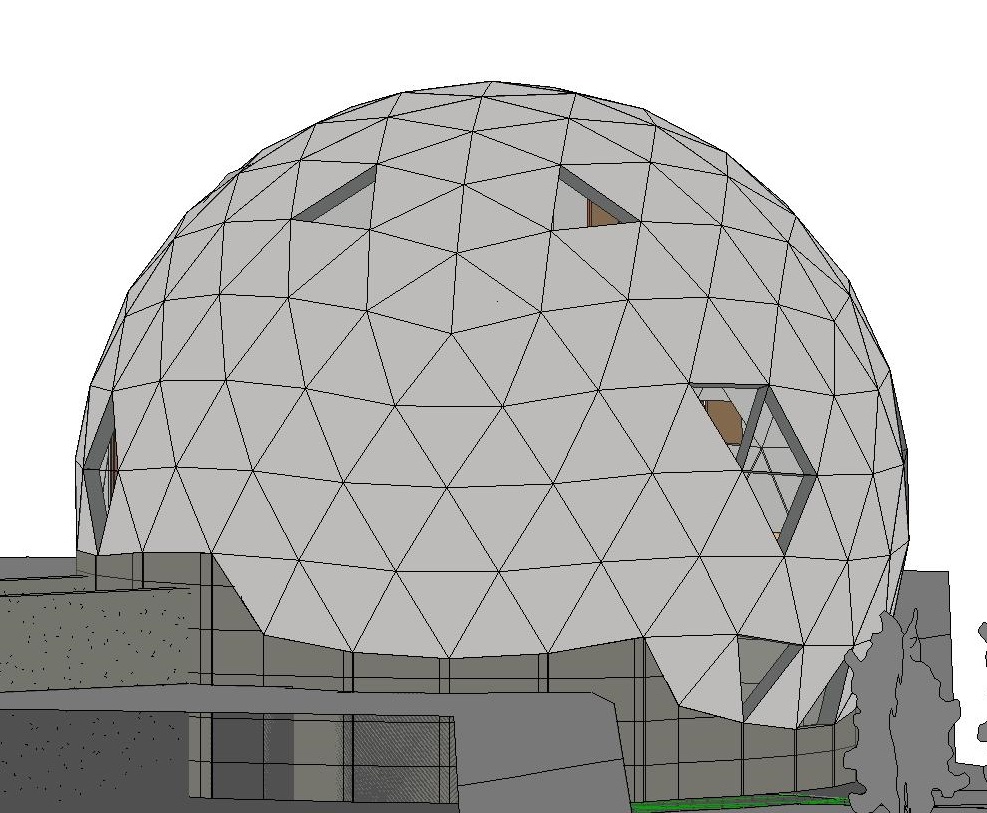
这种结构的基础是二十面体或八面体。 通常是规则的多面体。
就我而言,它恰好是二十面体,并且使用频率更高。 接下来,我们取一个面并将其替换为几个三角形,这些三角形的顶点位于一个球体上,该球体的中心与二十面体的中心重合。 听起来不太好。 让我们离题。
有一个很棒的计算器
www.acidome.ru ,它可以让您实时扭曲测量员。 以二十面体为基础,将频率设置为1(部分球体1/1)。

这是我们的主要二十面体。 频率是我们将断裂二十面体的每个边缘的数量。 我们设置3.4、5,没有任何事情变得清楚。 切换到屋顶模式并寻找五边形。 在那些我们具有二十面体顶部的地方-将有一个五边形。 在三个五边形之间是二十面体的面。

如果仔细查看测地线并知道要寻找的内容(通常是五边形),则结构的规则性将变得可见。 在蒙特利尔的生物圈中,您可以尽职调查找到五边形并计算频率。 我们的频率等于两个五边形之间的边数。
“大”三角形本身以及在二十面体顶部的顶点也具有结构。 在酸组屋面上,这是可见的颜色。 三角形相对于“大”三角形的中心对称放置。 它们类型的数量小于三角形的总数。 在5个唯一三角形出现的情况下9。

在设计房屋的过程中,我面临着在迪纳摩建造球体的任务。 此工具使您可以教Autodesk Revit处理复杂的表单。 这样的可视化编程环境。
谷歌搜索,我什至发现了一个在Dynamo中构建测地线球体的草图。 他建立了这个领域,但不是那个。
就是这个 当我们将二十面体的一个边缘分成小三角形时,这可以通过多种方式完成。 在acidome中,“拆分方法”开关是造成这种情况的原因。
找到的草图使用等弦方法建立了球体。 这是什么意思? 我们以二十面体的大三角形为单位,将其每个边缘分成所需数量的零件,将边缘上的点彼此连接,并获得一个平坦的三角形网格。 然后,我们将此网格投影到球体上。 一切都会好起来的,但是这些三角形本身的大小完全不同。 中央最重要的。 可以理解,“大”三角形的中心在我们与球体的最大距离处。 这是不好的,因为在这种情况下更难于优化材料的消耗。 将会有更多的浪费。
分割(具有相等弧度)的另一种方法假设我们建立在弧度的“大”三角形之上,并且已经将它们分为相等的部分。 方法不同,简单的投影无法做到。
该草图不适合。 我试图修复它,最后我不得不全神贯注地从事这项业务。
事实证明,除了视觉环境外,Dynamo还内置了Python。 我以前没有遇到过这种语言,但是我们的语言在哪里消失了? 最后,它只是一个工具。
然后会有几段代码,请注意,这是我在python中的问候世界,目标不是建立最有效的解决方案,而是建立正确的领域。
等弧线的方法。
我们采用二十面体的其中一个面,并从该三角形的角构建弧线。
for k, edge in enumerate(curves):

然后,我们将弧划分为相等的部分,并将弧上的点与新弧连接起来。 所有弧都有一个中心-球的中心。 点不是全部连接在一起,而是同一个名称。 在图片中看起来比在代码中简单。
for edge_index, point_list in enumerate(points): edge_arcs = [] for point_index, point in enumerate(point_list): next_edge_index = edge_index + 1 if len(points) == next_edge_index: next_edge_index = 0 end_point_index = n - point_index - 2 arc = Arc.ByCenterPointStartPointEndPoint(center_point, points[next_edge_index][end_point_index], point) if arc.SweepAngle > 90: arc = Arc.ByCenterPointStartPointEndPoint(center_point, point, points[next_edge_index][end_point_index]) arc_points_count = n - point_index - 1; pp = Arc.PointsAtEqualSegmentLength(arc, arc_points_count) for po in pp: on_arc_points.append(po) edge_arcs.append(arc) edges_arcs.append(edge_arcs)

糟糕,弧线不相交! 不太流畅的谷歌搜索使我读了一本书,证实了我的假设,即必须使用由圆弧交点形成的三角形的中心作为测地线边缘的顶部。 我也抽烟了酸组的来源,但是我不记得是否在那里找到了证实。 我记得那很有趣。
必须以某种方式找到这些中心。 这是三角形的中心,并不难,但是有必要了解这些三角形在点堆中的位置。 在我看来,连接最接近的点是最简单的选择。
for point in on_arc_points: distance = []

现在我们需要互连在不同阶段收集的点,这些点是测地线球的边缘的顶点。 在图片中,这些点清晰可见,但是当它们在阵列中时,一切都会变得更加复杂。 有几种选择,但是由于任务是花费最少的精力来获得有效的脚本,所以结果出来了:
段已准备就绪。 解决这个问题可能有某种正确的方法,但我自己铺了一条路。

然后该段展开,将其复制几次,然后复制,然后获得一个完整的球体。 这是其中之一:
v = Vector.ByTwoPoints(sphere_center, curves[0].StartPoint) for face_triangle in face_triangles: geodesic_sphere.append(Geometry.Rotate(face_triangle, sphere_center, v, 72))
该脚本很丑陋,我复制了几次,因为导出到Revit存在问题。 以为施工有问题。 结果,在迪纳摩论坛上,印度人提示了乌克兰人,一切都成功了!
现在,您可以构建任何频率和任何直径的球体。 将大小与酸组结果进行比较表明,所有内容都可以高精度收敛。 重复性好。

我还开始优化尺寸以最大程度地减少作物。 由于所有尺寸都在我手中,所以并不是那么困难。 结果,在5的频率下,球体的半径为5.65米,这样的尺寸使我可以有效地使用宽度为125 cm的材料,例如OSB板,金属板,绝缘材料,干式墙。 通过良好的优化,剪裁的数量将降至最低。 通过计算材料上三角形的布局可以达到最佳结果,但是我没有这样做。
此外,它更容易实现,因为Revit制作了复杂的形状并允许以与正方形平行相同的成功进行加工。
当然,困难并没有就此结束,但这是一个完全不同的故事。