
(
c )“银河星系”
分形不仅是美丽的自然现象。 根据
研究 ,分形结构的检查可以提高60%的抗应力性,这是根据生理参数测得的。 在短短一分钟内考虑大脑额叶皮层中的分形时,α波的活动就会增加-就像在冥想期间或感到轻微睡意时。
分形生物设计对人有镇定作用也就不足为奇了。 我们喜欢看云,看壁炉里的火焰,看公园的树叶……它是如何工作的? 科学家认为,我们眼睛搜索运动的自然过程是分形的。 当眼睛和分形物体的轨迹尺寸重合时,我们就进入了生理共振状态,因此大脑的某些部位的活动被激活了。
但并非所有分形都同样有用。 在本文中,我们将讨论分形维数及其对健康的影响。
生物分形

(
c )
自然界中分形的例子无处不在:从贝壳到松果。 每个分形都有一个
数学维 D。对于一个人来说,尺寸为1.3-1.5的分形最有用,并且自然界创建的大多数分形对象都具有这样的维。 人眼在
美学上被“调整”为对自然界中发现的这种分形的感知。

(
c )
树木是自然界中分形的典范。 从种子和松果到树枝和树叶,在森林生态系统的各个层面上都可以发现分形。 上图显示了一个“
害羞的树冠 ”-一种现象,当树冠没有接触时,形成森林冠层的局部区域。
从生物学的角度来看,树冠的这种排列是通过自然选择来解释的-叶子尽可能地间隔开,以最大程度地利用资源,尤其是光合作用的阳光。

(
c )
Romanesco意大利白菜采用超高效设计,可让您最大程度地暴露在阳光下,并在植物的细胞结构中运输养分。

(
c )
但是,这种卷心菜的尺寸是2.66。 通常,分数维是分形的关键特征。 此外,它们中的大多数位于直线(尺寸1)和二维曲面(尺寸2)之间的平面中。 指标越高,向三维物体的移动就越大(尺寸3)。
电脑游戏
三维分形是自然界中最稀有的分形之一。 在虚拟现实中认识他们要容易得多。 例如,在Marble Marcher游戏中-一个独特的街机游戏,您需要将球滚动到由单一综合算法创建的空间中的目标。 您在游戏中看到的几乎所有东西都不是由设计师创建的,而是由纯数学创建的。
Yedoma Globula是带有专有引擎的3D沙箱,您可以在其中探索程序生成的分形景观。
分形公式可用于计算机图形学中,以创建逼真的山脉,河流,森林和云层。 一切游戏都进行得更远:除了视觉组件外,游戏玩法的系统构成部分还使用了分形相似性。 几乎没有NPC字符。 您可以扮成一头猪,在绿色的斜坡上徘徊,遇到一棵橡树,然后变成一棵橡树,在独立的旅程中开始游戏。
小配件

(
c )
分形不仅可以在计算机游戏中或放松时用作“有用的东西”。 分形提出了一种减小手机天线尺寸的方法。 分形几何扩展了创建新的,更实用的设备的能力。
现在,分形被用于新一代卫星通信,物联网设备和其他项目中,用于接收,传输和转换无线电波。
建筑学

(
c )
分形甚至可以在不知不觉中被使用。 上图显示了伊朗清真寺圆顶的一部分。
在这里,您会发现许多伊朗学校,文化和宗教建筑天花板的照片,这些照片展示了令人难以置信的复杂分形浮雕和马赛克,装饰着精美的建筑元素。

(
c )
卡修拉荷的德维·贾加丹比神庙(Devi Jagadambi Temple)是分形建筑的典范。 印度和东南亚的许多其他寺庙都具有分形结构:主塔被较小的塔包围,而这些塔又被较小的塔包围。 依此类推,多达八个(有时甚至更多)级别代表了印度神话中的万神殿的各个方面。

(
c )
建筑中的分形并不是世界一部分的独特发明。 哥特式,文艺复兴时期和巴洛克式建筑的精美装饰,尤其是在大教堂中的装饰,经常表现出几个层次的分形复制和缩放。 自十二世纪末以来一直是欧洲建筑的典型代表。 拱形的交织更可能不是美观,而是具有实际重要性:它被设计用来加固窗户和墙壁以抵抗风压。

(
c )
自20世纪末以来,分形几何已被有意识地用于创建有趣且令人赏心悦目的外墙。 照片中-位于墨尔本市区(澳大利亚)的建筑计划中最复杂的建筑之一。 该综合体结合了文化,娱乐和商业项目。
危险的分形

(
c )
通过数学,自然和人为过程生成的大多数分形图像都基于视觉复杂性具有共同的美学品质。 视觉感知测试的参与者
更喜欢分形为精确自然来源的分形,其尺寸为1.3-1.5。 例如:波浪和云的尺寸为1.3,海岸线为1.05。

(
c )
但是,如果我们增加尺寸会怎样? 生成的对象并不总是很漂亮。 上图显示了尺寸为1.75的放电分布图(称为利希滕贝格图),该分布图是由非导电材料上的高压放电产生的。
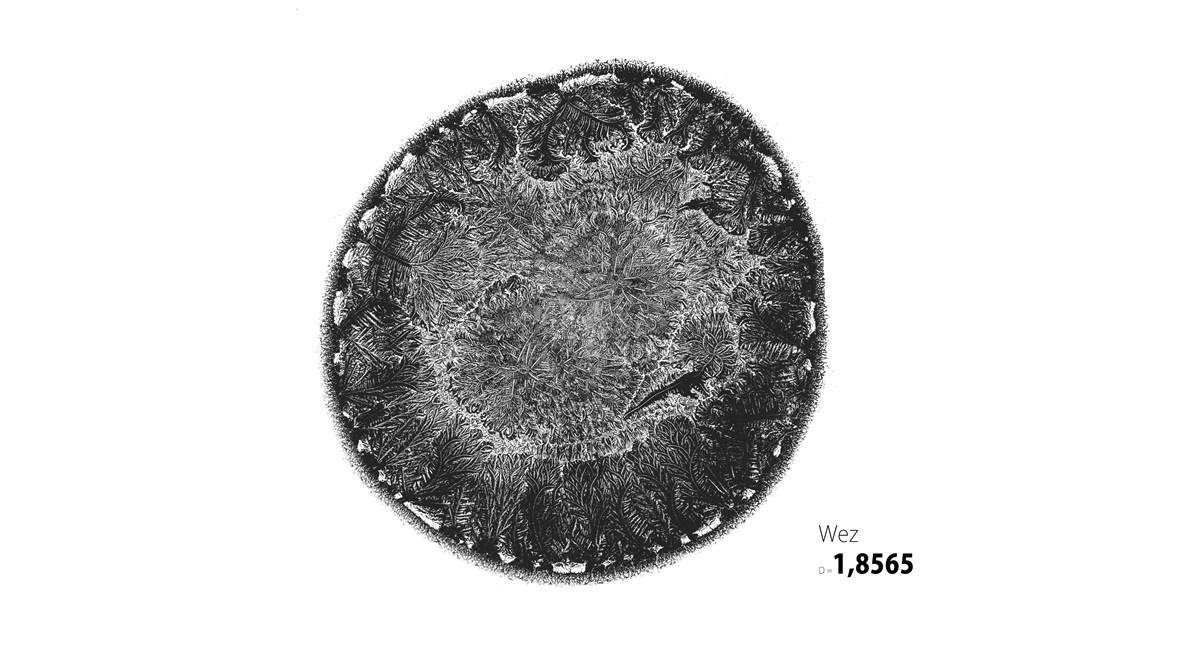
另一个排斥物体是通过显微镜拍摄的尺寸为1.8
的晶体结构的
分形产物 。
演示与软件
也许,像魔幻世界一样,他们没有探索过分形世界的地方。 Hartverdrahtet是2012年4 KB文件演示比赛的当之无愧的赢家。 作者Demoscene Passivist说,用程序生成的分形景观创建演示需要大约两个月的时间。
这是在场景中具有分形效果的最佳项目之一。 不幸的是,演示视频的质量非常差(由于年代久远),但是可以
下载演示并在计算机上运行。
要创建相似或其他分形的世界,不需要特殊的技巧。 有几个优秀的程序,可用来独立研究分形宇宙的特征。
XaoS开源项目 。 一个免费的,开放的,跨平台的工具,用于缩放和探索许多Mandelbrot和许多其他分形。
JWildfire 。 另一个跨平台(包括移动版本)的基于Java的开源程序,用于图像处理。 她以复杂的火状分形生成器而闻名。
曼德堡 Mandelbulb3D 。 出色的免费工具可用于创建三维分形,例如令人敬畏的
Mandelbrot Shell ,神秘的“盒子” Mandelbox等; Mandelbulber的功能和速度更高,但Mandelbulb3D的使用更简单。
在这里您将找到许多其他程序。
结论
分形研究
始于 1975年。 也就是说,事实上,我们才刚刚开始研究这个广阔而未知的领域。 分形不仅限于纯粹的数学,类似于音乐和诗歌的艺术,也不是解决实际问题的实用工具。 它们可以提供更多信息:例如,解释当前科学发展中我们无法理解的现象。 所有分形宇宙学都基于宇宙空间无穷大的理论以及根据分形维数原理(在2到3范围内)的天文物体的分布。