雨中跑步模拟
参赛作品
这一切都始于关于胆量的极具挑衅性的声明,这绝对不符合我对周围世界的想法:“如果在雨中奔跑,你会变得少湿-这是神话。” 换句话说,从该陈述得出结论,众所周知并且普遍接受在雨中奔跑的人比在相同的雨中步行相同距离的同一人湿得多。 但是,一些未经验证的不可靠消息来源则相反,如果您迅速从雨中走出来,您的湿润会更少。
该声明是在Mythbusters电视节目(第001集)中做出的。 我反复检查了几次-神话的措辞恰好是这样的: “一个人会在雨中奔跑而不是走路而变得干燥。”
更新:正如rezdm建议的那样, 有一段视频用不同的措词“在雨中值得跑步吗”
此外,验证的结果是破坏了这个神话,也就是说,正在奔跑的领导者比正在行走的领导者更湿! 就是说,这些未经检验和不值得信赖的消息来源,而且毫无意义。 在那一刻之前,在我的世界中,一切都恰好相反,为了减少潮湿,我试图跑到避难所。
此外,在几个季节之后,这个神话再次得到了证实和反对(第38集)。 但是,在第一和第二种情况下的结果都不太明显:所收集水的差异很小,与统计误差和天平上的测量误差几乎没有很大差异。 在第一个实验中,雨水是通过向悬挂在高机库天花板上的洒水器供水来产生的。 在第二个实验中,他们使用了从天上掉下来的东西。 在第二次实验后,清晰度变得更低。
我更喜欢第一个实验,因为条件是可以控制的,并且这些条件可以维持必要的时间。 在普通降雨的情况下,条件会不断变化-降雨可能会停止,降雨强度可能会改变,或者风会吹来。 我认为,有必要继续进行第一个研究:可以增加距离,可以使用降雨参数来减少统计误差并使结果更具说服力。 神话杀手》是一部出色的电视节目,但在这种特殊情况下,我想收看并重做所有内容。 对降雨的性质对所得湿气的影响这一主题特别感兴趣,因为通常在此类实验中会出现平均降雨,并且毕竟降雨是不同的。
正如通常发生的那样,我勇于克服这种毫无意义的,渴望重新进行实验并忘记了它的愿望。 但是,今年夏天在莫斯科地区,人们似乎对“我应该逃避雨水还是要冷静地走”的想法过于周到。 结果,我决定编写一个小项目,并借助计算机建模探索有趣的地方。 事实证明,在莫斯科地区,该主题现在在12月仍然有意义。
下一部分将描述发生的情况,但是在这里我需要对问题的历史说几句话。 在编写本文时,事实证明,“在雨中行走或奔跑”这个问题困扰了世界上许多极客一段时间。 显然,第一个浪潮是著名的科学普及者Yakov Isidovich Perelman在他的著作“娱乐力学”(他只看到1937年的第4版,但任务是在1930年开始的较早版本)中的第九章“ Treneye i Resistance” “ (是的,毕竟是20世纪初)最后一部分叫做“雨什么时候能变得更好 ?”,但实际上的任务是“在这种情况下,您还要多戴帽子吗?”。 区别在于-在本书中,我们仅谈论帽子从上方感知到的雨水成分,没有谈论垂直方向上与雨水的碰撞。 另外,在这项任务中,我们在雨中同时进行实验,而我们对相同的距离感兴趣。 毫无疑问,决策书中给出了正义,但是该部分的名称以及读者的独立结论可能会导致错误的结论和刻板印象。
佩雷尔曼(Perelman)之后,在远古时代流行的科学期刊上有文章, 而并非如此 ,然后是vidos, 现在翻译甚至在这里成为中心。 另一篇难以逾越的文章是2012年意大利物理学家佛朗哥·博西(Franco Bocci)在《欧洲物理学报》上发表的文章,该文章本身不太可能被很多人阅读,但它在媒体上的报道很多,例如,我认为这很有趣。 还有其他不同程度的研究。 事实证明,此问题的历史可能与问题本身一样有趣,并且可能是另一篇文章的主题。
造型
局限性和假设
建模的本质是对现实感知的有目的的简化和抽象。 本文中介绍的模型也不例外。 进一步的文字可能表明,由于任务的特殊性,身体,认知的局限性以及与作者的宗教,种族,政治,性和其他偏好有关的限制是一种特定的假设或限制(换句话说,那些东西,这不仅太懒惰,而且太懒惰,无法解释为什么我没有制作它们。
限制和假设的示例:单元中的液滴数量为一个(最大强度极限),所有液滴的大小均相同,假定一个人在行走和跑步时不会挥动手臂和腿部(额和水平投影区域始终相同),从鞋子上取水不考虑背面,实验中没有风等
太空与人

空间篇
该模型由两个对象表示,即空间和人。
该空间是一个长方体,分成大小为1x1x1 cm的立方体。
空间的宽度等于人的宽度:在实验中,不考虑有风和侧风的情况,因此,计算人的宽度以外的空间是没有意义的。
该空间的高度比一个人的高度大一个水平的立方体层-即一厘米,在这一层中开始记录液滴,该液滴在下一瞬间将落在一个人身上,或者进一步落入一个未被人占据的空间中。
空间的长度(范围)应等于距离的长度,但这是非常不经济的,因为对于实验而言,您只需要知道一个人上方的空间状态以及他前面的几层空间。 因此,在项目中循环使用该空间,并选择其长度,以便当人们在第一垂直层完全通过该空间时,将更新所有单元格。 换句话说,出现在该人背后紧挨的图层中的下落应该有足够的时间落到地面上,直到该人再次用脸靠近该图层时为止。 因此,在正确选择空间长度的情况下,新鲜的水滴将始终滴落到人身上。
应当注意的是,在实验过程中,空间的长度被确定一次,然后不改变,因此,对于长度的初始设置,选择参数的比例以使在所有情况下长度都足够(最大的人的速度和最小的掉落率)。
可以用不同的方式来想象实验的空间,例如,一个封闭的走廊,但是我更喜欢将它想象成一个矩形的光点,从一个从一侧照到另一侧并随人移动的灯笼。 记录进入点内光线的每个液滴。 这种方法使我们能够将人在雨中奔跑的无限物理空间的概念与实验空间分开-一个虚构的三维网格,在每个实验时刻都检查其每个单元的状态。 在本文中,单词“ space”用于第二种含义。
在程序中,空间由三维字节数组表示。 数组中元素的索引对应于单元在空间中的坐标(长度,高度,宽度),元素本身描述状态。 只能有两种状态-单元中有雨滴或单元为空。
也可以将空间想象成一组水平的降雨层,以及人们在移动时遇到的一系列垂直层。 在程序中,有一些类-包装负责这些表示。
人
项目中的人只是一个矩形框。 对于实验,我们主要感兴趣的是它在水平面上的投影以计算从上方掉落的水滴,并在垂直于运动方向的垂直平面上的投影以计算人向前移动时遇到的水滴。 还使用了负责其在空间中位置的坐标,以及正面和顶部积水的计数器。
为了估计水平投影的面积,最早引用的内容之一是使用紧急部的某些法规 。 在那里,人的水平投影由椭圆表示,其轴向尺寸为0.5 m(人在肩膀上的宽度)和0.25 m(人的厚度)。 这似乎是真的,因此我选择了一个几乎相同面积的矩形(S椭圆= pi * a * b S = 3.14 *(50/2)*(25/2)〜982平方厘米,矩形48 x 20 = 960平方厘米) 如上所示,这些数据用于确定空间的宽度和范围。 我没有找到一个人的垂直投影的定义,因此,对于成长,我的取值略小于平均值-160厘米,人的尺寸很容易在项目中改变,但是实验仅在一组参数上进行。 由于这个问题对我而言似乎并不那么有趣-首先,您不太可能以某种方式影响雨中的这些参数,其次,找出哪种体质最适合在雨中淋湿可能对某人不利。 我将其与限制和假设联系起来。
人体速度:以2.196 km / h为下限; 从这里开始,显然这些数据用于假肢,上限为43.9 km / h- 当前记录的最快行驶速度 。
关于下雨
项目中的降雨是在空间中发生的过程,它具有自己的特征:液滴大小,下降速度,强度。
根据维基百科,雨滴的直径不能小于0.5毫米,因为它将不再是雨,而是细雨,并且不超过6-7毫米,在这种情况下,水滴会分裂成较小的水滴。
根据同一文章,对于小液滴,液滴的滴落速度为2至6 m / s,对于直径为5 mm的液滴,液滴的滴落速度为9至30 m / s。 尺寸为5mm至7mm时,由于这样大的液滴呈降落伞的形式,并且空气阻力增加,因此下降率降低。 液滴的下落速度不仅取决于液滴本身的大小,还取决于其下落的条件-我认为它取决于空气的密度,是否存在上升或下降的气流等。
该项目确定了下降速率与直径长度的线性关系:在直径从0.5到5 mm的范围内,速度从2 m / s线性增加到30 m / s(DropSize * 6.22-1.11),在从5毫米到7 mm的范围内,速度从强度相同((10-DropSize)* 6.22-1.11),超出0.5-7 mm范围时,不进行实验。
实验中使用的线性相关性与现有的世界情况并不矛盾,但是它是有限的,因此是一种假设。 例如,项目中的5毫米下降对应于30 m / s的速度-在现实世界中可能会发生(根据Wikipedia),但在现实世界中,直径为5毫米的下降可能会以9 m / s的速度下降得更慢。 如果某人感兴趣并决定自己进行实验,则可以将依赖关系更改为其他任何依赖关系,甚至可以尝试其中的几种。 在此项目中,由于时间有限,此功能的使用量非常有限。
强度是降雨的另一个有趣且重要的特征。 强度通常以毫米/小时表示。 每小时1毫米意味着一小时内一层1毫米厚的水将掉落在1平方米的水平面上。 不难计算出这层水的体积为一升。 也就是说,一毫米/小时等于一小时每平方米一升。 有时在天气预报中,当他们想要描述灾难的规模时,它们仅表示毫米-这是在整个降雨期间落下的水层的计算高度。 在项目中,以及在文章中,将使用度量单位-每小时毫米。
根据维基百科,降雨强度通常为0.25 mm / h(雨水)至100 mm / h(雨水)-在这些值内进行了实验。
关于空间滴的分布:
我想简单地谈一谈有趣的一点。 在设计阶段,计划将上部水平层填充为如下所示的液滴:一旦计算出在单元格中出现液滴的概率,然后对层中所有单元格进行排序,则基于此概率的随机化器将在单元格中放置或不放置液滴。 将概率计算为该层中所需液滴数与该层中细胞总数的比值。 考虑到已经将空间减小到最小的事实,这种方法似乎很合理。 但是,在开始实验之前,我决定估计每单位空间的液滴数量(发生的概率相同),这就是发生的情况:下面是面积为1平方米,厚度为1厘米的层中液滴数量的图表,具体取决于液滴的大小,每张图表都对应于其强度:

在水平轴上-墨滴的大小,在垂直轴上-墨滴的数量。 垂直轴是对数的,因为液滴数量的分布非常大。 如此大的散布可以通过以下事实来解释:液滴体积与其线性尺寸(直径)的三次方成正比,并且随着液滴尺寸的增加,液滴的下降率也会增加。 因此,液滴直径的变化很小,液滴的数量变化很大(例如,对于80 mm / h的降雨强度,直径为0.8 mm,每层需要大约215滴液滴,当液滴直径加倍时,最大可达1.6 mm每层12滴)。
现在,关于优化:从图表中可以看出,即使具有最小的液滴体积和最大强度,每万个单元的液滴数目也不会超过2 x千,在大多数情况下液滴数目小于100,并且如果液滴的直径大于3 mm,则每层的液滴数目少于一个。 因此,遍历该层的每个单元,从而最终仅出现一个液滴是不经济的。 一种更经济的选择是计算图层中的液滴数量,然后将它们随机散布到整个图层中。 唯一的麻烦是所选单元格已满的情况(在这种情况下,递归看起来不错)。 如果我们将所有存储单元的存储都添加到其中,以便随后进行层的清洁,则可以在CPU使用上略有增加的情况下,节省大量CPU资源。
雨水模拟过程
建模过程发生在一个主要周期中。 此循环的每次迭代都对应一个最小时间间隔(刻度)。 系统的每个报价状态都已更新和固定。 滴答声的持续时间对应于雨滴穿过一层空间(在我们的示例中为1厘米)的持续时间,因此程序中的一个滴答声可以对应于现实生活中的不同时间间隔,具体取决于输入参数(或更确切地说,取决于水滴的下落速度)。 下面描述了每次迭代中发生的动作:
该项目中的降雨过程如下:首先,在顶层随机填充水滴(请参见上文),将其设为第n层。 n- , — n-1, . : n-2 n-1, n-1 n-, n- , . , , , (, , ), , , .
( ) , . , , ( ). . , , , , , ( ) , , .
, , ( ), , , , .
( ), ( ). , . , , . , . — , . , , , , . , , .
, , . , , , .
, , , .
, .
, – « , , , ?» – « ?»
. «», , , , : , ?
. « ?»
. « – , ? ?»
, . : , , , . 1 , .
, , . 2,2 /, 23,04 /, , 43,88 /. . – , .
, , . – , , , . , . , . , , . : (0.6 ), (7 ), 5 () «» (1.4 ). 10 (10 – 100 /). 1, 50 100 (, , ). . , , .

:
对于每场比赛:-收到的水量;-总滴数;-顶部的液滴数量(体积);-前面的液滴数量(体积);-每跳的平均增长;-一口气从上方平均增长;-每组一个水平位移的平均增益(总/仅水平/仅正面)-在不同速度下获得的体积差。-我想到的其他指标。结果与结论
, . , , 12 , 36 1 . 32 529 927 , 2 . , , , .

. , . , : « ?» : . .
, , « , ?» — , , - . :

( 20 /) 1 , 3.2 ~ 26% . , : 0,0005841873 1 1712 , 1 7,06 . – , , , , , . .

20 100 , . 23 / 43 /. , , « , ». : , , , .
, « ?».
, , :

0.6 5 , , 5 – 7 ( 7 , 5). , , .

, – , . , ( ), : , , .
– , .
, 50/ ( ). , :
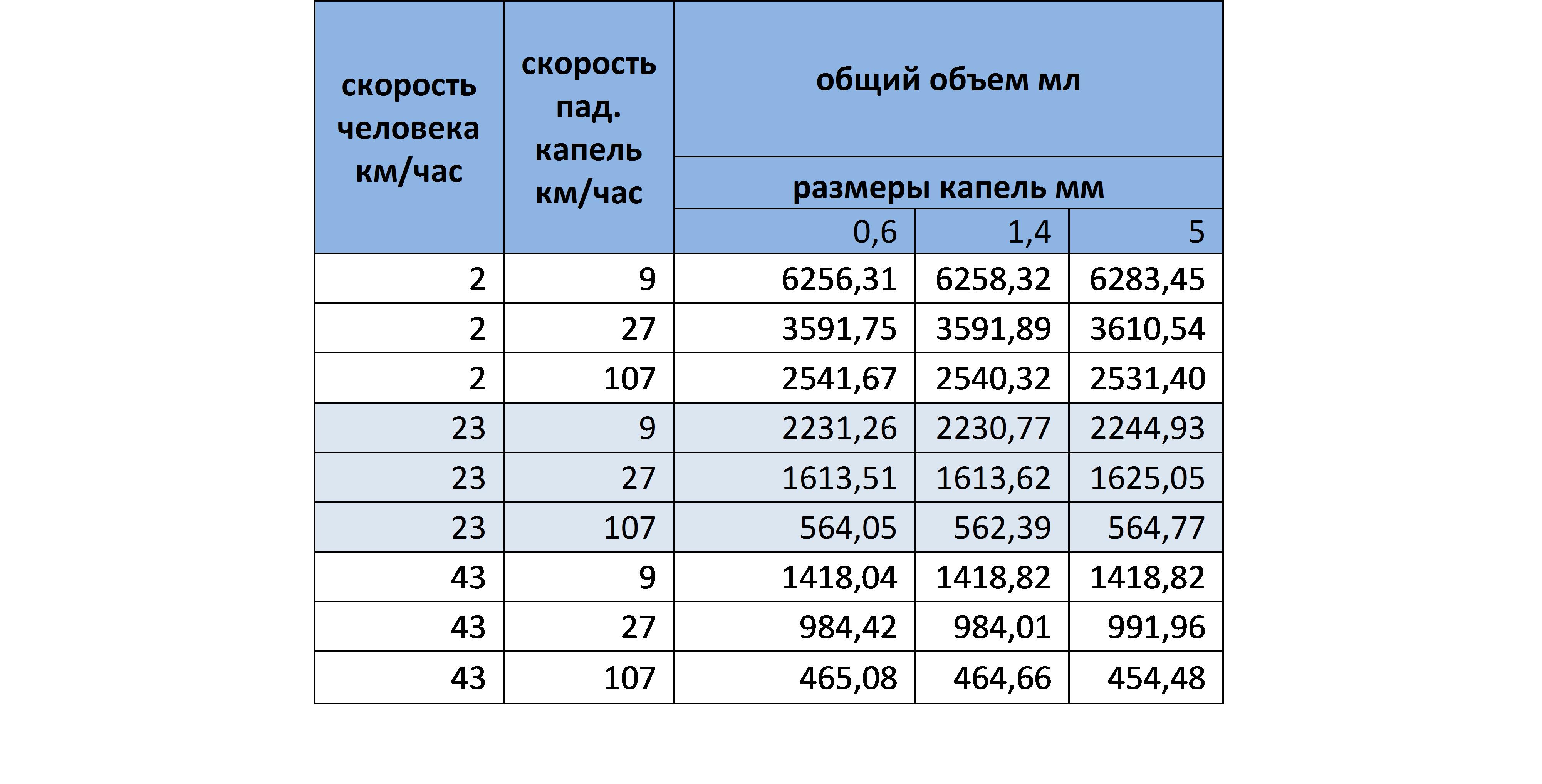
, , , , .
- , . , . , , , , , , .
: « – , ? ?».
, , , , .
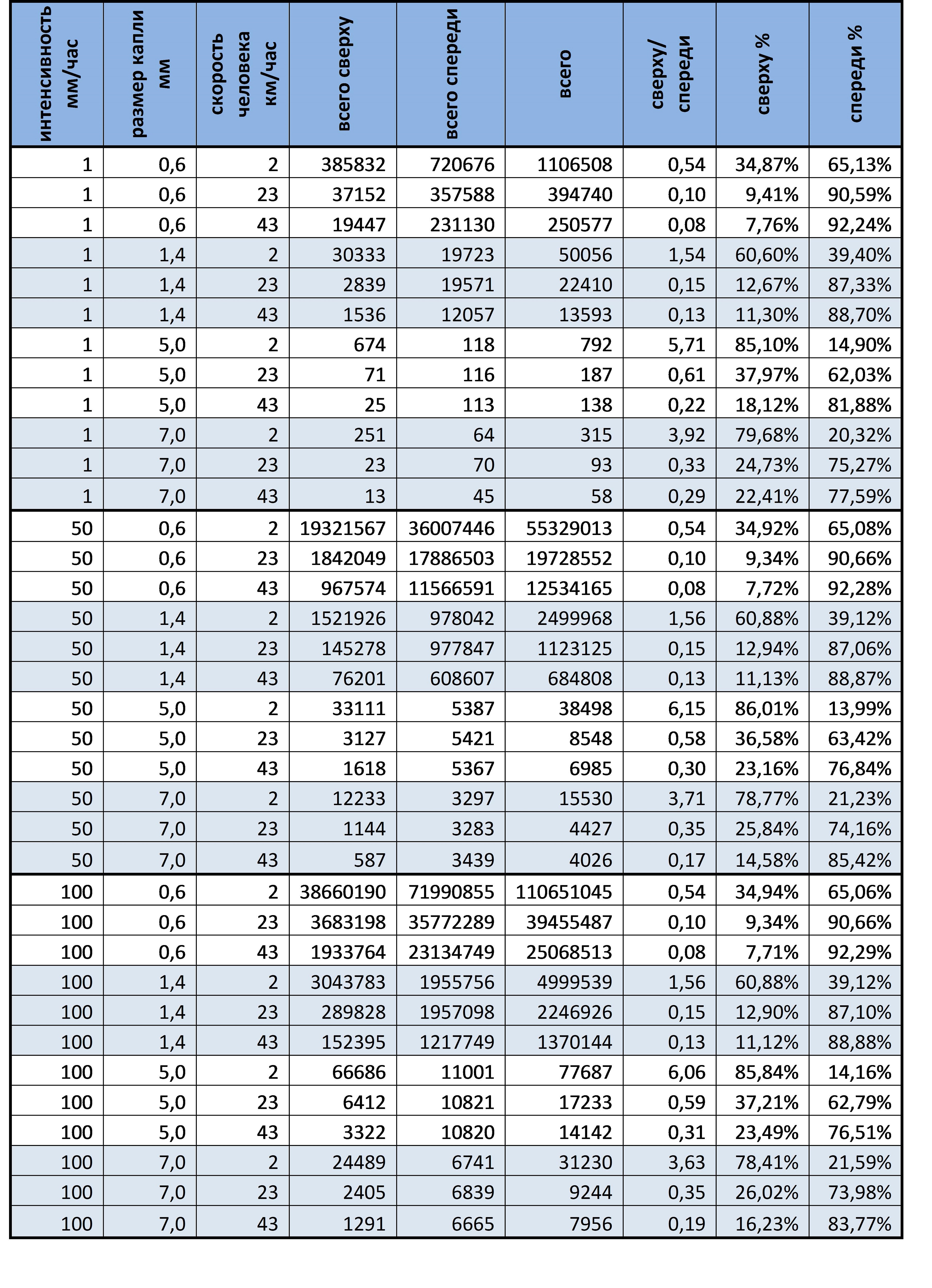
, :
1) – , ( ).
2) , , ( 2 / 50 %).
3) , , , , ( ).

4) , . , ( ):

这意味着滴落率越大,Katya越会影响最终收集的水量。换句话说,如果您陷入倾盆大雨的倾盆大雨中,则越早跑到避难所,弄湿的东西就越少。反之亦然,如果在大街上有毛毛雨,很多小液滴悬在空中,那么就没有奔跑的感觉,这不会对最终结果产生太大影响。
因此,第四个问题的答案是“一个人将从上方还是从正面收集更多的水?” 它的读法是:一个人在雨中行走可以从上方和前方收集更多的水,该比例主要取决于其速度,但是滴落率有很大的影响。 一个人的速度越大,从上方落到他身上的水滴就越少。
仅此而已。 正如古生物学家史考特博士所说,研究自然并做出自己的发现,伙计们。 :)
PS:文本,模型,结果,提出的问题和答案以及在其他任何地方都可能有错误,因此如果有人要检查,仔细检查,重复,补充,反驳,戳戳,我会将项目发布到公共领域鼻子等-欢迎您github.com/sv-kopylov/raindrops-pub.git 。
PPS本文是续篇,现在是有关娱乐计算机建模的系列文章, 这里是第一篇。