表通常包含大量逻辑字段，无法索引所有逻辑字段，并且这种索引的有效性很低。 然而，对于在SQL中使用任意逻辑表达式，多维索引机制是合适的，将在目录下进行讨论。
在SQL中，主要在两种情况下使用逻辑字段。 首先，当您确实需要二进制属性时，例如，在交易表中进行“买卖”。 这些属性很少随时间变化。
其次，记录描述记录的
状态机的
状态 。 可以理解，对应于表记录的逻辑对象经过一系列状态，其状态和它们之间的转换由所应用的逻辑确定。 一个简单的例子是“软删除”技术，当记录没有物理销毁，而是仅标记为已删除时。
如果机器很复杂，那么可能会有很多这样的字段，在
我们的一张表中，有58个（+14已过时）这样的字段（包括标志集），这与众不同。 这不是最初计划的，但是随着产品的发展和外部需求的变化，相应的机器的发展，开发人员的来去去去，分析师的变化……在某个时候，获得一个新的标志也许比了解所有的复杂情况更安全。 此外，历史数据已经积累，其条件必须保持适当。
异位在某些方面，这与进化过程相似，当基因组中存储了大量信息/机制时，乍一看根本不需要，但是却不可能摆脱它们。 另一方面，值得尊重这些机制，因为正是它们使进化的前辈得以生存（包括在
大灭绝期间）并赢得了进化种族。 再次，谁知道进化将引领我们，未来将证明有用。
放置标志不仅意味着添加相应类型的字段，还意味着在自动机的操作中将其考虑在内，它会影响什么状态，以及它所参与的转换。 实际上，它看起来像这样：
- 一个流程或一系列流程，我们称它们为“作者”，以初始状态（可能是其中一种初始状态）创建新记录
- 许多过程，我们称它们为“阅读器”，它们不时读取处于所需状态的对象
- 许多过程称为“处理程序”，监视特定状态，并根据应用的逻辑更改这些状态。 即 操作状态机。
为了选择处于特定状态的记录，很少需要通过布尔字段之一进行过滤。 通常，这是一个完整的表达式，有时不平凡。 似乎您需要为这些字段建立索引，而SQL处理器会找出答案。 但不是那么简单。
首先，可能有很多布尔字段；将它们全部索引会太浪费。
其次，它可能没有用，因为 每个字段的选择性较低，并且联合概率不包括在SQL处理器的统计信息中。
假设在表T1中有两个布尔字段：F1和F2，以及查询
select F1, F2, count(1) from T1 group by F1, F2
发出
即 尽管根据F1和F2，对和错的可能性均相等，但组合（对，错）仅在千分之一中出现。 结果，如果我们分别为F1和F2编制索引
并强制在查询中使用它们 ，则SQL处理器将必须读取两个索引的一半并交叉结果。 读取整个表并计算每一行的表达式可能会更便宜。
而且，即使您收集了已完成请求的统计信息，也没有太大用处。 专门针对负责机器状态的字段的统计信息非常浮动。 实际上，任何时候“处理程序”可能会来并将一半的线路从状态S1传输到S2。
为了使用这样的表达式，多维索引会提示自己，该算法的算法
较早就
提出了，并被证明是相当不错的。
但是首先，您需要弄清楚任意逻辑表达式将如何变成对索引的查询。
析取范式
对多维索引的单个查询是一个限制查询空间的多维矩形。 如果该字段参与了请求，则会为其设置一个限制。 如果不是，则此坐标中的矩形仅受此坐标的宽度限制。 逻辑坐标的容量为1。
此类索引中的搜索查询是＆（连接词）链，例如表达式：v1＆v2＆v3＆（！V4），等效于v1：[1,1]，v2：[1,1]，v3：[1， 1]，v4：[0,0]。 所有其他字段的范围为：[0,1]。
鉴于此，我们的目光立即转向
DNF-逻辑表达式的规范形式之一。 有人认为，任何表达都可以表示为文学连词的析取。 这里的文字是指逻辑字段或其取反。
换句话说，通过简单的操作，任何逻辑表达式都可以表示为多个查询对多维逻辑索引的析取。
但是有一个。 在某些情况下，这种转换可能导致表达式大小成指数增长。 例如，从
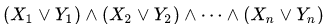
导致2 ** n项的表达式。 在这种情况下，应用程序开发人员应考虑自己所做工作的物理含义，而对于SQL处理器，如果连接数超出合理范围，则您始终可以拒绝使用逻辑索引。
多维索引算法
对于多维索引，使用了基于带有边2的超三次单纯形的自相似编号曲线的属性，
事实证明 ，这种曲线的两个版本具有实际的重要性-Z曲线和Hilbert曲线。
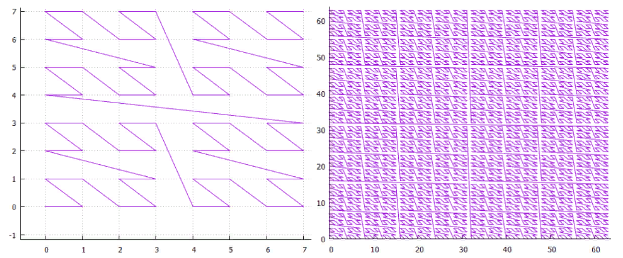图1二维Z曲线，3和6次迭代
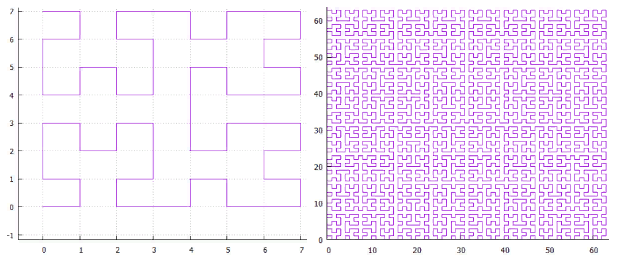图2二维希尔伯特曲线，分别进行3和6次迭代- 侧面为2的N维单纯形具有2 ** n个顶点，它们之间有（2 ** n-1）个过渡。
- 单形的基本迭代将单形的每个顶点转换为较低级别的单形。
- 完成必要的迭代次数后，我们可以构造任何大小的超立方晶格。
- 此外，该晶格的每个节点都将具有其自己的唯一编号-从编号起点开始沿编号曲线的路径。 而且，该格子的每个节点在每个坐标中具有一个值。 实际上， 编号曲线将多维点转换为适合用常规B树索引的一维值 。
- 位于任何级别的单纯形内的所有节点都在同一间隔内，并且此间隔不与同一级别的任何单纯形相交。
- 因此，可以将任何搜索矩形（框）划分为少量的高次子查询，在每个子查询中，可以通过一次搜索/遍历读取索引。
- 为此，我们添加了使用B树进行低级工作的魔力，以免发出无用的请求，并且...算法已经准备就绪。
这是实际的工作方式：
图3二维索引（Z曲线）中的示例搜索图3显示了将原始搜索范围划分为子查询和找到的点。 使用了二维索引，该索引基于范围为100,000,000点[1,000,000，1,000,000]的随机，均匀分布的集合。
逻辑多维索引
既然我们在谈论多维索引，那么该考虑一下多维索引的数量了吗？ 有客观限制吗？
当然，由于B树具有页面组织并且要成为树，因此必须确保至少两个元素适合页面。 如果您将页面设为8K，则存储一项不能超过4K。 在没有压缩的4K中，大约可以容纳1000个32位值。 这是很多事情，超出了任何合理应用程序的限制，我们可以说实际上没有物理限制。
还有另一面，每个额外的维度绝不是免费的，它会占用磁盘空间并减慢工作速度。 从“物理意义”的角度来看，应将同时更改的字段包含在同一索引中，并且对它们的搜索也应同时进行。 连续索引所有内容没有意义。
逻辑字段是不同的。 如我们所见，相同的机制可以包含数十个逻辑字段。 而且存储/读取成本很小。 试图将所有逻辑字段收集在一个索引中，然后看看会发生什么情况，这是一种诱惑。
的确，有一些细微差别：
- 到目前为止，在索引值中，不同坐标的数字混合在一起，键的最低有效数字是坐标的最低有效位。因此，索引期间字段的顺序无关紧要。
- 现在，花了一位来存储一个逻辑字段的值。 即 一些逻辑字段将移至键的末尾，而某些逻辑字段将移至键的开始。 这意味着按部分字段进行过滤将非常有效，而对于某些字段则将非常低效。 实际上，如果我们以最低顺序进行搜索，则必须阅读整个索引才能得到答案。 但这（最有可能）比阅读整个表格回答同样的问题要好。
- 有一个选择问题-所有逻辑字段都是相等的，但有些逻辑字段将比其他逻辑字段更相等。 从一般的角度来看，有必要看一下统计数据的失真，特定场的真假比率与平衡的距离越远，其值出现的时间越长。
- 按编号曲线类型划分的分区消失了，如果较早需要在Z曲线和Hilbert曲线之间进行选择，则单位数据上没有实际差异。
- 空值。 基于NULL不是未知值，但是没有任何值的事实，此类记录不应包含在索引中。 在一维索引中，会发生这种情况。 但是在我们的情况下，可能会发现某些逻辑字段包含值，而某些逻辑字段不包含值。 结果，我们不能将其放在索引中，因为 搜索算法不知道如何使用三元逻辑。 因此，这样的记录应该不可能插入表中（顺便说一下，如果存在多维索引，不一定是逻辑索引）
预期逻辑多维索引在某些情况下可能无法非常有效地工作。 严格来说，如果有太多数据落入搜索区域，则任何索引都可能效率低下。 但是对于逻辑多维索引，这是由于上述对字段顺序的依赖性加重了，而为了获得较小的结果，您必须读取整个索引。 就实际存在的问题而言，只有实验可以证明。
数值实验
建立索引：
- 索引将是128位，即 建立在128个逻辑字段上
- 并将包含2 ** 30个元素
- 索引元素的值将是0到2 ** 30之间的数字
- 索引元素的关键字将是相同的数字，即向左移48位。 逻辑字段48至78将以相同的顺序填充数字的数字
- 结果，我们在键的中间得到30个重要的逻辑字段，其余位将被填充0
- 每个布尔字段具有相等的统计信息true / false
- 在统计上都是独立的。
搜索：
- 每个实验都对应于几个连续逻辑字段的选择以及它们的搜索值分配。 不是因为算法只能在条带中搜索，而是因为可以更清晰地可视化实验结果，所以我们只有两个维度-条带的宽度及其位置
- 共有24个系列的实验。 在每个系列中，我们将寻找相应宽度N（1到24位）的逻辑字段带取值为true的值。
- 在每个系列中，将有一个子系列的实验，其中选定宽度的逻辑字段条带从条带的开始到30个重要逻辑字段的移位S不同。 子系列中的总计（30-N）个实验。
- 在每个实验中，搜索满足条件的所有索引元素，即 在[48 + S，48 + S + N -1]区间中编号的字段将在区间[1,1]中搜索，其余在[0,1]区间中搜索
- 搜索从冷启动开始
- 结果是读取的磁盘页数，包括缓存（4096页缓存）
- 正确操作的控制有两种方式-找到的元素数量必须等于2 **（30-N），并且在找到的值中您可以检查相应的数字
所以
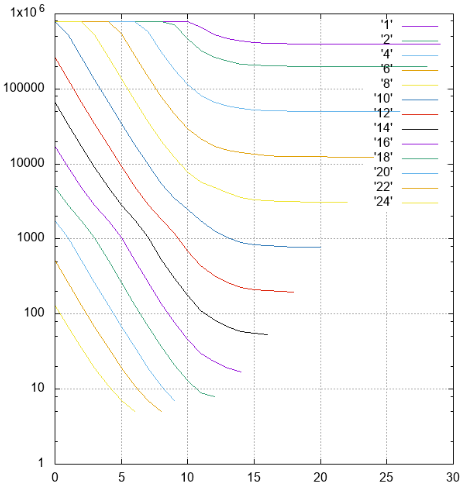图4结果，不同系列中读取的页面数通过Y-推迟读取的页面数。
在X上-条形从最年轻的（48）类别移至高级。 不同宽度的条纹用不同的颜色签名和标记。
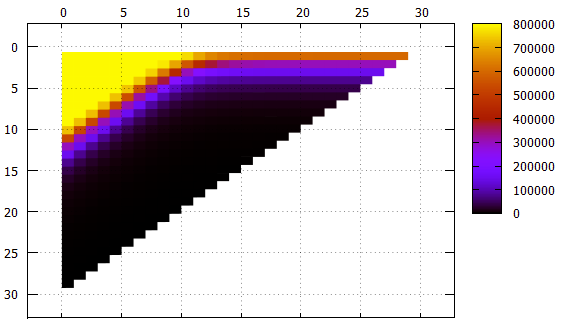图5与图4相同的数据，另一个视图X波段移位
Y-带宽
应该注意的是：
- 尽管这在图片中不直接可见，但是索引可以正常工作，但在找到的元素数量和元素本身的内容中都可见
- 所有宽度不超过10且偏移量为0的条纹都需要连续读取索引
- 具有1到18宽度且随着移位增加的条纹达到整个索引大小的渐近线2 **（-N），这是合乎逻辑的
- 对于渐近线的较宽波段-树的高度，读数不能少
- 在索引表页面上放置了超过1000个元素，这在宽度为10的条带中可见，当移动0不再需要读取整个索引时，可以跳过某些页面
- 低级过滤效果惊人。 考虑一条宽度为10的条带。理想的搜索选项是平移20（总共30个有效字段），如果前缀中根本没有未定义的字段，则可以用单个光束找到数据。 在这种情况下，在搜索过程中将读取大约1/1000的索引-779页。
中间情况是移位10，我们有10个未知字段的前缀和后缀。 页数为2484，仅比理想情况下差三倍。
即使在最坏的情况下，如果偏移量为0（前缀为20个未知字段），您也可以跳过某些页面。
总体而言，即使在这种荒谬的情况下，多维索引算法也可以被认为是有效的。
但是，从逻辑索引的角度考虑，最不成功的选择是-所有独立逻辑字段中的等概率状态。实验真实数据
交易表，总计278,479,918行，来自测试循环之一的数据。
下表中某些查询的结果：
读取/处理单个页面平均需要0.8毫秒。
无需描述特定查询的含义，它们只是为了演示可操作性。 顺便确认一下。
但是，在该技术可以实际应用之前，还有很多工作要做。 因此，待续。