深度强化学习：如何教蜘蛛走路

今天，我将告诉您如何应用强化深度学习算法来控制机器人。 简而言之，我将告诉您如何创建“带有神经网络的黑匣子”，该黑匣子在输入端接受机器人体系结构，并输出可以在输出端对其进行控制的算法。

解决方案的核心是具有优势得分（通过通用优势估算 （GAE））的优势演员评论 （A2C）算法。

精简版包括数学，TensorFlow实现以及关于哪种步行算法的大量演示。

内容：

- 结论

挑战赛

在本文中，我们将教机器人在MuJoCo模拟中行走。 我们将跳过创建机器人模型和环境的Python接口的步骤说明，因为 那里没有什么有趣的。 要了解，只需看一下MuJoCo本身的演示以及Gym OpenAI中MuJoCo环境的来源。

在输入处，代理程序将具有来自MuJoCo的许多数字：相对位置，旋转角度，速度，机器人身体各部分的加速度等。 总共约有800个功能。 我们使用深度学习方法，不会理解它们的实际含义。 最主要的是，在这组数字中，将有足够的信息，以便业务代表可以了解他的情况。

在输出中，我们将期望18个数字-机器人的自由度数，这意味着固定肢体的铰链的旋转角度。

最后，特工的目标是使剧集的总回报最大化。 如果机器人崩溃或经过3000步（15秒），我们将结束该情节。 每一步骤将根据以下公式奖励代理商：

即 代理商的目标将增加其坐标 $$$x$ 并且直到情节结束才堕落。

因此，任务设置为： 查找功能 $$$\ pi：\ R ^ {800} \到\ R ^ {18}$ 为此情节的回报将是最大的 。 听起来不太对吗？ :)让我们看看深度强化学习如何处理此任务。

为什么要进行强化学习？

解决步行机器人运动问题的现代方法包括经典机器人技术，包括最佳控制和轨迹优化两部分 ：LQR，QP，凸优化。 阅读更多： 波士顿动力团队在Atlas上的帖子 。

这些技术是一种“硬编码”，因为它们需要将任务的许多细节直接引入控制算法中。 它们中没有学习系统-优化是“当场”进行的。

另一方面，强化学习（以下简称RL）在算法中不需要假设，从而使该问题的解决方案更加通用和可扩展。

强化学习声明

来源

在RL问题中，我们将主体与环境的相互作用视为一对对（状态，奖励）以及它们之间的过渡- 行动的序列。

定义术语：

• $$$\ pi（a_t | s_t）$ - 政策 ，代理人行为策略，条件概率，
• $$$a_t \ sim \ pi（\ cdot | s_t）$ -从分布中将动作视为随机变量 $$$\ pi$ ，
  我们可以将政策视为一项职能 $$$\ pi：状态\到动作$ ，但我们希望使代理行为随机化，以利于探索 。 即 很有可能我们没有完全执行代理选择的动作。
• $$$\ tau$ -代理跟踪的轨迹，序列 $$$（s_1，s_2，...，s_n）$ 。

代理的任务是使预期收益最大化：

现在我们可以制定RL问题，找到：

在哪里 $$$\ pi ^ *$ 是最优政策。

在OpenAI的材料中阅读更多内容： OpenAI Spinning Up 。

政策梯度

值得注意的是，将RL问题作为优化问题的严格说明使我们有机会使用已知的优化方法，例如梯度下降 。 试想一下，如果我们可以通过模型参数获取预期的收益梯度，那将是多么酷： $$$\ nabla_ \ theta J（\ pi_ \ theta）$ 。 在这种情况下，更新比例的规则很简单：

这正是所有策略梯度方法的想法。 这个梯度的严格结论有些严格。 我们不会在这里写它，但是会保留来自OpenAI的精彩材料的链接。 渐变如下所示：

因此，我们模型的损失将是这样的：

回想一下 $$$R（\ tau）= \ sum_ {t = 0} ^ T r_t$ 和 $$$\ pi_ \ theta（a_t | s_t）$ -这是当她进入时我们模型的输出 $$$s_t$ 。 出现负号是因为我们要最大化 $$$J$ 。 在训练过程中，我们将分批考虑梯度并添加梯度以减少差异 （随机环境造成的数据噪声）。

这是一种称为REINFORCE的有效算法。 而且他知道如何为一些简单的环境找到解决方案。 例如， “ CartPole-v1” 。

考虑代理代码：

class ActorNetworkDiscrete: def __init__(self): self.state_ph = tf.placeholder(tf.float32, shape=[None, observation_space]) l1 = tf.layers.dense(self.state_ph, units=20, activation=tf.nn.relu) output_linear = tf.layers.dense(l1, units=action_space) output = tf.nn.softmax(output_linear) self.action_op = tf.squeeze(tf.multinomial(logits=output_linear,num_samples=1), axis=1) # Training output_log = tf.nn.log_softmax(output_linear) self.weight_ph = tf.placeholder(shape=[None], dtype=tf.float32) self.action_ph = tf.placeholder(shape=[None], dtype=tf.int32) action_one_hot = tf.one_hot(self.action_ph, action_space) responsible_output_log = tf.reduce_sum(output_log * action_one_hot, axis=1) self.loss = -tf.reduce_mean(responsible_output_log * self.weight_ph) optimizer = tf.train.AdamOptimizer(learning_rate=actor_learning_rate) self.update_op = optimizer.minimize(self.loss) actor = ActorNetworkDiscrete() 

我们对此结构有一个小的感知器：（observation_space，10，action_space）[对于CartPole，这是（4，10，2）]。 tf.multinomial允许您选择随机加权的操作。 要采取行动，您需要致电：

 action = sess.run(actor.action_op, feed_dict={actor.state_ph: observation}) 

因此，我们将训练他：

 batch_generator = generate_batch(environments, batch_size=batch_size) for epoch in tqdm_notebook(range(epochs_number)): batch = next(batch_generator) # Remainder: batch item consists of [state, action, total reward] # Train actor _, actor_loss = sess.run([actor.update_op, actor.loss], feed_dict={actor.state_ph: batch[:, 0], actor.action_ph: batch[:, 1], actor.weight_ph: batch[:, 2]}) 

批处理生成器在环境中运行代理并积累数据以进行培训。 批处理的元素是这种元组： $$$（s_t，a_t，R（\ tau））$ 。

编写好的生成器是一项单独的任务，其中主要的困难是与单个模拟步骤（甚至是MuJoCo）相比，调用sess.run（）的成本相对较高。 为了加快工作速度，您可以利用神经网络批量运行并使用许多并行环境这一事实。 与在单个环境中相比，即使顺序地在一个线程中启动它们也将带来明显的加速。

 # Vectorized environments with gym-like interface from baselines.common.vec_env.subproc_vec_env import SubprocVecEnv from baselines.common.vec_env.dummy_vec_env import DummyVecEnv def make_env(env_id, seed): def _f(): env = gym.make(env_name) env.reset() # Desync environments for i in range(int(200 * seed // environments_count)): env.step(env.action_space.sample()) return env return _f envs = [make_env(env_name, seed) for seed in range(environments_count)] # Can be switched to SubprocVecEnv to parallelize on cores # (for computationally heavy envs) envs = DummyVecEnv(envs) # Source: # https://github.com/openai/spinningup/blob/master/spinup/algos/ppo/core.py def discount_cumsum(x, coef): """ magic from rllab for computing discounted cumulative sums of vectors. input: vector x, [x0, x1, x2] output: [x0 + discount * x1 + discount^2 * x2, x1 + discount * x2, x2] """ return scipy.signal.lfilter([1], [1, float(-coef)], x[::-1], axis=0)[::-1] def generate_batch(envs, batch_size, replay_buffer_size): envs_number = envs.num_envs observations = [[0 for i in range(observation_space)] for i in range(envs_number)] # [state, action, discounted reward-to-go] replay_buffer = np.empty((0,3), np.float32) # [state, action, reward] rollout lists for every environment instance rollouts = [np.empty((0, 3)) for i in range(envs_number)] while True: history = {'reward': [], 'max_action': []} replay_buffer = replay_buffer[batch_size:] # Main sampling cycle while len(replay_buffer) < replay_buffer_size: # Here policy acts in environments. Note that it chooses actions for all # environments in one batch, therefore expensive sess.run is called once. actions = sess.run(actor.action_op, feed_dict={actor.state_ph: observations}) observations_old = observations observations, rewards, dones, _ = envs.step(actions) history['max_action'].append(np.abs(actions).max()) time_point = np.array(list(zip(observations_old, actions, rewards))) for i in range(envs_number): # Regular python-like append rollouts[i] = np.append(rollouts[i], [time_point[i]], axis=0) # Process done==True environments if dones.all(): print('WARNING: envs are in sync!! This makes sampling inefficient!') done_indexes = np.arange(envs_number)[dones] for i in done_indexes: rewards_trajectory = rollouts[i][:, 2].copy() history['reward'].append(rewards_trajectory.sum()) rollouts[i][:, 2] = discount_cumsum(rewards_trajectory, coef=discount_factor) replay_buffer = np.append(replay_buffer, rollouts[i], axis=0) rollouts[i] = np.empty((0, 3)) # Shuffle before yield to become closer to iid np.random.shuffle(replay_buffer) # Truncate replay_buffer to get the most relevant feedback from environment replay_buffer = replay_buffer[:replay_buffer_size] yield replay_buffer[:batch_size], history # Make a test yield a = generate_batch(envs, 8, 64) # Makes them of equal lenght for i in range(10): next(a) next(a)[0] 

生成的代理可以在动作空间有限的环境中播放。 此格式不适合我们的任务。 控制机器人的代理必须从 $$$\ R ^ n$ 在哪里 $$$n$ -自由度数。 （ 或者您可以将动作空间划分为多个空白，并获得具有离散输出的任务 ）

对角高斯政策

对角高斯策略方法的本质是使模型产生n维正态分布的参数，即 $$$\ mu_ \ theta$ -垫子 等待和 $$$\ sigma_ \ theta$ -标准偏差。 一旦代理需要采取行动，我们就会从模型中询问这些参数，并从该分布中获取一个随机变量。 所以我们让代理退出 $$$\ R ^ n$ 并使其随机。 最重要的是，在输出端固定了分配类之后，我们可以计算 $$$\日志（\ pi_ \ theta（a_t | s_t））$ 因此政策梯度。

注意：可以固定 $$$\ sigma_ \ theta$ 作为超参数，从而减小输出尺寸。 实践表明，这不会造成太大的伤害，但是相反，它可以稳定学习。

阅读更多有关随机政策的信息 。

代理代码：

 epsilon = 1e-8 def gaussian_loglikelihood(x, mu, log_std): pre_sum = -0.5 * (((x - mu) / (tf.exp(log_std) + epsilon))**2 + 2 * log_std + np.log(2 * np.pi)) return tf.reduce_sum(pre_sum, axis=1) class ActorNetworkContinuous: def __init__(self): self.state_ph = tf.placeholder(tf.float32, shape=[None, observation_space]) l1 = tf.layers.dense(self.state_ph, units=100, activation=tf.nn.tanh) l2 = tf.layers.dense(l1, units=50, activation=tf.nn.tanh) l3 = tf.layers.dense(l2, units=25, activation=tf.nn.tanh) mu = tf.layers.dense(l3, units=action_space) log_std = tf.get_variable(name='log_std', initializer=-0.5 * np.ones(action_space, std = tf.exp(log_std) self.action_op = mu + tf.random.normal(shape=tf.shape(mu)) * std # Training self.weight_ph = tf.placeholder(shape=[None], dtype=tf.float32) self.action_ph = tf.placeholder(shape=[None, action_space], dtype=tf.float32) action_logprob = gaussian_loglikelihood(self.action_ph, mu, log_std) self.loss = -tf.reduce_mean(action_logprob * self.weight_ph) optimizer = tf.train.AdamOptimizer(learning_rate=actor_learning_rate) self.update_op = optimizer.minimize(self.loss) 

培训部分没有什么不同。

现在，我们终于可以看到REINFORCE将如何处理我们的任务。 此后，探员的目标是向右移动。

缓慢但肯定地朝他的目标迈进。

奖励去

请注意，我们的渐变中还有其他成员。 即每一步 $$$t$ 在权衡对数梯度时，我们使用整个轨迹的总奖励。 因此，根据代理人过去的成就来评估其行为。 听起来不对，不是吗？ 所以这个

会变成这个

找到10个差异:)

尽管这些成员的存在不会在数学上破坏任何东西，但它给我们带来了很大的噪音。 现在，在训练过程中，座席将仅注意在特定操作后获得的那些奖励。

由于这种改进，平均奖励有所增加。 其中一位特工学会了使用前肢来实现自己的目标：

通过增加批评减少差异

进一步改进的实质是减少由于介质状态之间的随机过渡而产生的噪声（方差）。

这将帮助我们添加一个模型，该模型将从状态开始预测代理商收到的平均奖励金额 $$$s$ 到轨迹的尽头，即 值函数。

如果我们的政策从特定状态开始游戏，则“价值”功能将显示预期收益。 与Q功能相同，只需修复第一个动作即可。

提出批评

这是使用奖励奖励时的外观：

现在，对数梯度的系数不过是Value函数的样本。

我们用来自特定轨迹的一个样本权衡对数梯度，这不好。 我们可以使用某些模型（例如神经网络）来近似值函数，并从中询问必要的值，从而减少方差。 我们将此模型称为批评家（批评） ，并将与政策并行研究。 因此，梯度公式可以写成：

我们减少了方差，但同时，由于神经网络会产生近似误差，因此将偏差引入了算法。 但是在这种情况下的妥协是好的。 机器学习中的这种情况称为偏差方差折衷 。

评论家将对在环境中收集的奖励性样品进行价值函数回归分析。 作为误差函数，我们采用MSE。 即 损失看起来像这样：

验证码：

 class CriticNetwork: def __init__(self): self.state_ph = tf.placeholder(tf.float32, shape=[None, observation_space]) l1 = tf.layers.dense(self.state_ph, units=100, activation=tf.nn.tanh) l2 = tf.layers.dense(l1, units=50, activation=tf.nn.tanh) l3 = tf.layers.dense(l2, units=25, activation=tf.nn.tanh) output = tf.layers.dense(l3, units=1) self.value_op = tf.squeeze(output, axis=-1) # Training self.value_ph = tf.placeholder(shape=[None], dtype=tf.float32) self.loss = tf.losses.mean_squared_error(self.value_ph, self.value_op) optimizer = tf.train.AdamOptimizer(learning_rate=critic_learning_rate) self.update_op = optimizer.minimize(self.loss) 

现在，训练周期如下所示：

 batch_generator = generate_batch(envs, batch_size=batch_size) for epoch in tqdm_notebook(range(epochs_number)): batch = next(batch_generator) # Remainder: batch item consists of [state, action, value, reward-to-go] # Train actor _, actor_loss = sess.run([actor.update_op, actor.loss], feed_dict={actor.state_ph: batch[:, 0], actor.action_ph: batch[:, 1], actor.weight_ph: batch[:, 2]}) # Train critic for j in range(10): _, critic_loss = sess.run([critic.update_op, critic.loss], feed_dict={critic.state_ph: batch[:, 0], critic.value_ph: batch[:, 3]}) 

现在，该批处理包含另一个值，即由注释者在生成器中计算出的值。
即 批处理的类型是这样的： $$$（s_t，a_t，V ^ \ pi_ \ psi（s_t），\ sum_ {t'= t} ^ T r_ {t'}）$ 。

在周期中，没有什么东西会限制我们从训练评论家到收敛 ，因此我们采取了几步梯度下降的方法，从而改善了Value函数的逼近度并减少了偏差。 但是，此方法需要大批量，以避免重新培训。 关于学习政策的类似说法是不正确的。 它应该从学习环境中获得即时反馈，否则我们可能会发现自己处以罚款政策以采取尚未采取的行动。 具有此属性的算法称为on-policy 。

政策梯度基准

可以证明，在梯度中，可以放很多其他有用的函数 $$$t$ 。 这些功能称为基准 。 （ 这一事实的结论 ）以下功能可以很好地作为基准：

资料来源： GAE纸 。

不同的基线会根据任务给出不同的结果。 通常， 优势函数及其近似值可带来最大的利润。

这背后甚至还有一点直觉。 当我们使用Advantage时，我们会根据代理商认为其执行的操作的平均水平好坏多少的比例对代理商进行罚款。 代理在环境中发挥的越好， 他的标准就越高 。 理想代理将发挥良好作用，并评估其所有动作，使其“优势”等于0，因此坡度等于0。

通过价值函数评估优势

回顾优势的定义：

目前尚不清楚如何明确学习这种功能。 有一个技巧可以解决，它将把Advantage函数的计算减少到Value函数的计算。

定义 $$$\ delta_t ^ V = r_t + V（s_ {t + 1}）-V（s_t）$ -时间差残差（ TD-残差 ）。 不难得出这样的函数近似于Advantage的结论：

这种概念上复杂的更改会引起代码中的变化不大。 现在，评论家将不提交价值函数，而是提交用于策略培训的优势评估。

生成的算法称为Advantage Actor-Critic 。

 def estimate_advantage(states, rewards): values = sess.run(critic.value_op, feed_dict={critic.state_ph: states}) deltas = rewards - values deltas = deltas + np.append(values[1:], np.array([0])) return deltas, values 

可以观察到获得的作用剂有信心的步态和四肢的同步使用：

广义优势估计

相对较新的文章（2018年），“ 使用广义优势估计的高维连续控制 ”，通过值函数提供了对优势的更有效评估。 它进一步减少了方差：

其中：

• $$$\ delta_t ^ V = r_t + V（s_ {t + 1}）-V（s_t）$ -TD残差
• $$$\伽玛$ -折扣系数（超参数），
• $$$\ lambda$ -超参数。

解释可以在出版物本身中找到。

实现方式：

 def discount_cumsum(x, coef): # Source: # https://github.com/openai/spinningup/blob/master/spinup/algos/ppo/core.py """ magic from rllab for computing discounted cumulative sums of vectors. input: vector x, [x0, x1, x2] output: [x0 + discount * x1 + discount^2 * x2, x1 + discount * x2, x2] """ return scipy.signal.lfilter([1], [1, float(-coef)], x[::-1], axis=0)[::-1] def estimate_advantage(states, rewards): values = sess.run(critic.value_op, feed_dict={critic.state_ph: states}) deltas = rewards - values deltas = deltas + discount_factor * np.append(values[1:], np.array([0])) advantage = discount_cumsum(deltas, coef=lambda_factor * discount_factor) return advantage, values 

当使用小批量时，该算法会收敛到某些局部最优值。 在这里，特工用一只爪子当拐杖，其余的则推开：

在这里，特工没有使用跳跃，而只是快速地用四肢指法。 您还可以看到他的举止，如果他犹豫，他会转身继续跑步：

最好的经纪人，他在本文的开头。 稳定的跳跃，在此期间所有四肢都脱出表面。 平衡能力的发展使代理能够在发生错误的情况下全速校正轨迹：

陷阱

机器学习以错误空间的大小而著称，该错误空间可能会产生并获得完全不起作用的算法。 但是RL将问题带到了一个全新的高度。

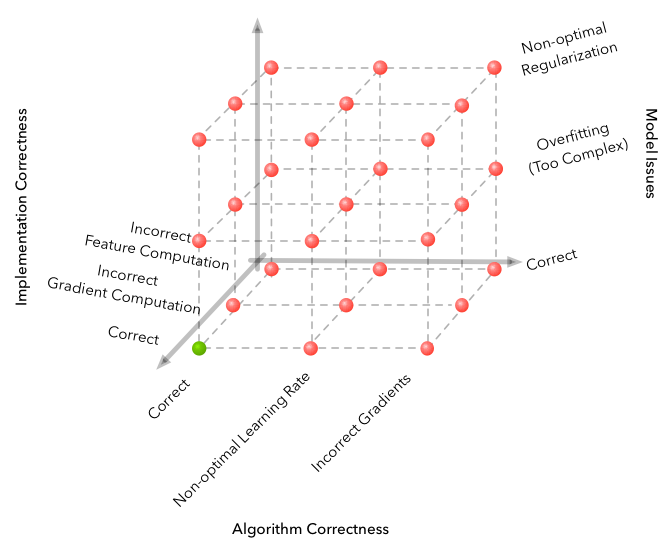
来源

这是在开发过程中遇到的一些困难。

1. 该算法对超参数非常敏感。 将学习率从3e-4更改为1e-4时，学习质量发生了变化。 画面发生了根本性的变化-从完全不收敛的算法到视频中的最佳算法。
2. 批次的大小与DL的其他区域完全不同。 如果在图像分类中，您可以选择32-256个批次的大小，而增加它的结果不会有太大变化，那么最好花几千，3,000个工作来完成我们的任务，再者，从缺乏收敛性到好的算法。
3. 学习最好运行几次，有时随机种子并不幸运。
4. 在如此复杂的环境中学习需要花费大量时间，并且进步也不统一。 例如，学习了8个小时的最佳算法，其中3个算法的结果比随机基线差。 因此，在测试算法时，最好从较小的算法开始，例如健身房的玩具环境。
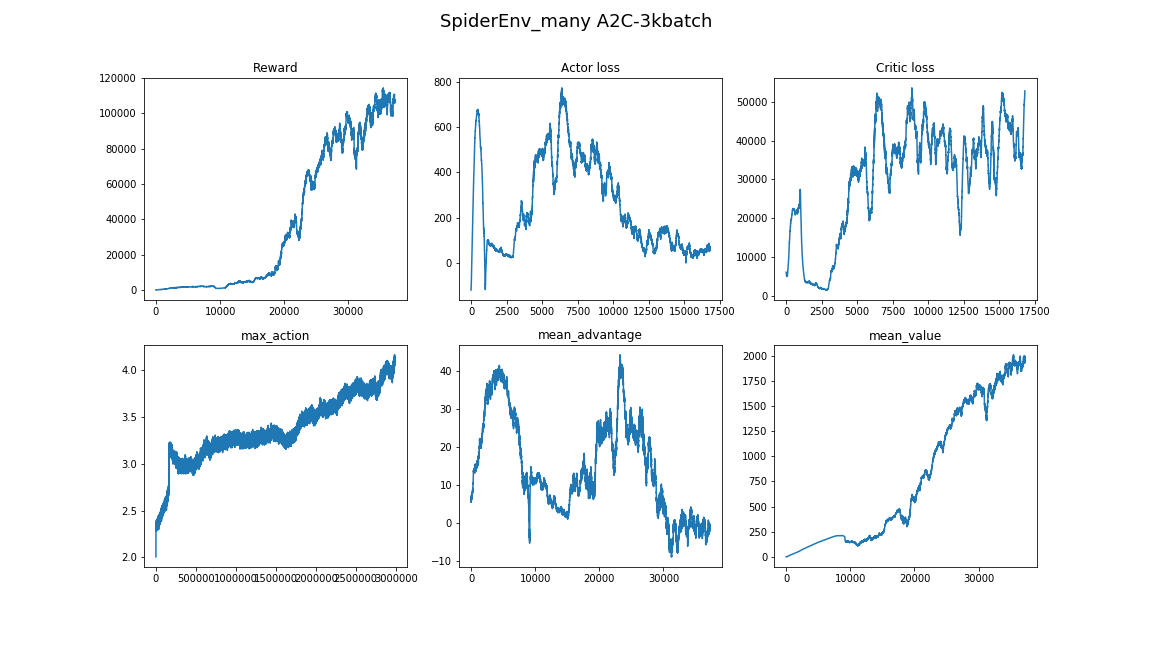
5. 查找超参数和模型体系结构的一种好方法是浏览相关文章和实现。 （主要是不要再培训）

您可以从本文中了解有关Deep RL细微差别的更多信息： 深度强化学习尚不可行 。

结论

最终的算法令人信服地解决了该问题。 找到功能 $$$\ pi：\ R ^ {800} \到\ R ^ {18}$ ，灵活而自信地控制机器人。

逻辑上的继续将是研究A2C，PPO和TRPO算法的近亲。 它们提高了样品效率 ，即 算法的收敛时间，它们能够解决更复杂的问题。 最近在机器人上组装了Rubik's Cube的是PPO +自动域随机化。

在这里，您可以找到文章中的代码： repository 。

我希望您喜欢这篇文章，并从深度强化学习今天能做的事情中得到启发。

感谢您的关注！

有用的链接：

• 欢迎使用Deep RL入门！
• CS 294：深度强化学习，2017年秋季
• CS 285：深度强化学习，决策和控制
• 使用广义优势估计的高维连续控制
• OpenAI基线：强化学习算法的高质量实现

感谢pinkotter ， Vambala和andrey_probochkin ， pollyfom和suriknik为该项目提供的帮助。
特别是， Vambala和andrey_probochkin用于创建一个很酷的MuJoCo环境。