社区计数“什么？” 在哪 什么时候？”（ChGK）或在朋友面前进行过几次握手？

哈Ha！

新年假期是度过美好时光的好时机 与IT休息一下 在您最喜欢的爱好中使用专业技能。 在体育ChGK评分网站上四处寻找 ，我发现了一个出色的API，可让您获取所有锦标赛的所有比赛数据。 因此，我想到了建立专家社区图并在地理位置分散且严格离线的社区中测试六次握手理论的想法。 在katom的图形图片和无用的统计信息下。

首先，有一个简短的教育计划，什么是体育ChGK。

资料检索

我们假设玩家在一张游戏桌上至少玩过一次，就彼此熟悉。 得益于良好的API，下载有关所有锦标赛和所有球队的数据不是问题。

在剧透之下，甚至没有使用美丽的汤，只要求。 带有所有源代码的jupyter笔记本将在本文结尾。

url = 'https://rating.chgk.info/api/tournaments.json/?page={}' df = pd.DataFrame(columns=['name', 'start']) for i in range(1, 7): data = requests.get(url.format(i)).json() for item in data["items"]: df.loc[item["idtournament"]] = (item["name"], item["date_start"]) df.to_csv('tournaments.csv') 

仍然可以下载所有锦标赛的游戏花名册并记住所有熟人。 最初，我计划将联合游戏的事实存储在DataFrame中，但是添加新记录的速度令人沮丧。 因此，我们将从元组（id1，id2）开始设置，其中id1，id2是彼此熟悉的玩家的标识符。 同时，消除重复项。

 df = pd.read_csv('tournaments.csv').set_index('Unnamed: 0') url = 'https://rating.chgk.info/api/tournaments/{}/recaps.json' links = set() for id in df.index: teams = requests.get(url.format(id)).json() for team in teams: t = team["recaps"] for i in range(len(t)): for j in range(i + 1, len(t)): first = int(t[i]["idplayer"]) second = int(t[j]["idplayer"]) if first < second: links.add((first, second)) else: links.add((second, first)) #    sleep(1) clear_output(wait=True) display('Current tournament: ' + str(df.index.get_loc(id) + 1) + '/' + str(len(df))) display('Links total: ' + str(len(links))) 

获取图形并探索连接的组件

因此，数据准备结束了，该创建图表了！ 为此，我们将使用networkx库，该库的功能对于我们的集群已经足够了。

 players = itertools.chain(*links) G = nx.Graph() G.add_nodes_from(players) for t in links: G.add_edge(*t) print(nx.info(G)) 

现在，ChGK社区中有大约20万人，平均而言，一名职业专家与12个人一起玩过：

 Number of nodes: 198145 Number of edges: 1206076 Average degree: 12.1737 

现在是时候确定日期图中有多少个相连的组件了。 Networkx具有一个名为connected_components的强大功能，它可以满足您的需求：

 clusters_l = [len(c) for c in sorted(nx.connected_components(G), key=len, reverse=True)] print(clusters_l[:20]) 

几乎四分之三的玩家都位于一个连接的组件中，其余的则分成非常小的子图。 有八千多个。

 [145922, 153, 124, 74, 72, 56, 50, 47, 42, 40, 39, 39, 38, 38, 37, 36, 36, 36, 36, 35] 

即使在对数尺度上，主要成分的主导地位也令人印象深刻。 在X轴上-分量的数量从最大到最小，在Y轴上-分量的大小（该轴为对数）。

是什么导致人员在连接的组件中分布不均？ 我认为关键是：

• 一小群人第一次来玩游戏，从而形成了4-6人的小团体；
• 如果城市已经有一个大型社区，那么这样的集群将很快与主要社区合并-只有一个人需要为主要集群中的团队效力；
• 如果在ChGK市刚刚出现，该集群的寿命将更长，因为 为来自主集群的团队效力更加困难。

该过程类似于云中雨滴的形成：大雨滴吸引小雨滴并迅速生长。

在处理主要组件之前，让我们看一下位于第一或第九位的组件（我认为主要组件为零）。 我们检验了这些组成部分中的人来自同一城市的假设。 鉴赏家对这座城市没有依恋（在现代世界中这是合乎逻辑的）。 但是，您可以查看他上次参加比赛的球队的本国港口

 for i in range(1, 10): _g = list(sorted(nx.connected_components(G), key=len, reverse=True)[i]) s = pd.Series() p_url = 'https://rating.chgk.info/api/players/{}/tournaments.json' t_url = 'https://rating.chgk.info/api/teams/{}.json' for player in _g: data = requests.get(p_url.format(player)).json() for item in data: team_id = data[item]["tournaments"][0]["idteam"] data = requests.get(t_url.format(team_id)).json() town = data[0]["town"] s.at[len(s)] = town print(' #{}'.format(i)) print(s.value_counts()) 

汇总板：

是的，小型集群几乎完全来自一个城市。 请注意与卢森堡有关的72名坦波夫居民的组成部分。 在第七和第九位的是来自Gorno-Altaysk的组件，由于某种原因它们没有相互连接。 我不难想象，有两个ChGK灰氏族（例如Montecca和Capulet）在争夺城市控制权的斗争。
我想在不久的将来这些组件将合并为主要组件 但会继续战斗 。

连接的主要组成部分

因此，我们进入了主要部分。 我们将获得所需的子图，并查看其统计信息：

 subgraph_v = list(sorted(nx.connected_components(G), key=len, reverse=True)[0]) subgraph = G.subgraph(subgraph_v) print(nx.info(subgraph)) 

事实证明平均连接数更多。

 Number of nodes: 145922 Number of edges: 1070504 Average degree: 14.6723 

每个玩家的最大连接数是多少？

 for t in sorted(G.degree, key=lambda x: x[1], reverse=True)[:10]: print(' {}   {} '.format(t[0], t[1])) 

  42511   818   15051   798   29800   678   23020   666   16581   662   5328   657   29887   651   15811   645   30352   605   1055   602  

坦白说，我对这些数字感到有些震惊。 如果您每次都与一个新团队一起比赛，那么您将需要818/5≈164场比赛才能获得第一名。 难以置信。
我们会记住该评级的前两名专家，并将进一步利用他们的沟通技巧。
让我们估计一个普通专家有多少个最熟识的人：

 _count = 50 values = nx.degree_histogram(subgraph) plt.figure(figsize=(16, 8), dpi=80) plt.plot(range(_count),values[:_count],'ro-') # in-degree plt.xlabel(' ', fontsize=18) plt.xticks(range(0,_count, 5)) plt.ylabel(' ', fontsize=18) plt.title(' ', fontsize=22) plt.show() 

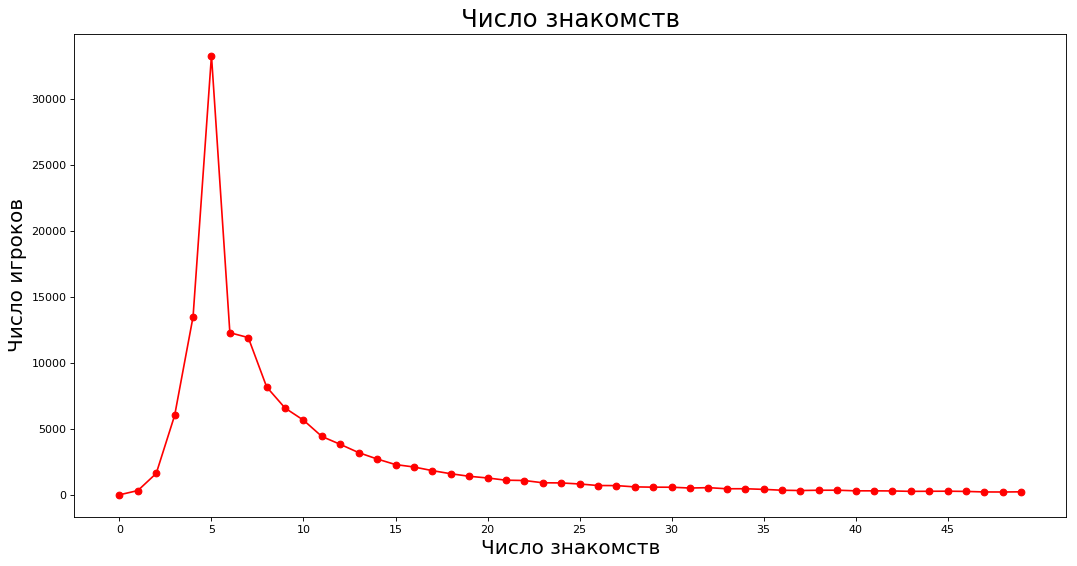
在X轴上-最接近的相识数，在Y轴上-具有相应相识数的专家数。 例如，大约有40,000位专家，每位都有五个熟人。
请注意，时尚界有5位熟人（有趣的是，最多可以有6个人在桌子旁）。 同时，相识数的算术平均值为14.67，中位数为7。事实是，上述评级的绅士们大大高估了平均值。 如果一百个人不参加ChGK比赛，而一个人有800个熟人，那么平均而言，他们将参加ChGK比赛。

到玩家的距离

因为 计算这样一个图形的直径有些困难 ，让我们做起来更容易：列出几个参与者的列表，找出他们与其他专家之间最短距离的最大值。 作为这些玩家，我聘请了几位知名专家，我本人，一位随机玩家和两名熟识最多的专家（请参阅上面的评分）。 这是发生了什么：

 famous_players = {9808: ' ', 5195: ' ', 25882: ' ', 29333: ' ', 118622: ' ', 42511: ' ', 15051: ' ', 118621: ' '} for key in famous_players: print('{}: {} -      ' .format(famous_players[key], nx.eccentricity(subgraph, v=key))) 

  : 12 -        : 12 -        : 12 -        : 12 -        : 13 -        : 12 -        : 13 -        : 13 -       

事实证明，严格意义上的六次握手理论（任何两个人被不超过五个级别的共同朋友分开）的说法是不正确的。 图的直径很可能是13-14。
措辞较弱（ 平均两个人之间的共同朋友最多不超过五个等级）怎么办？

 for key in famous_players: paths = nx.shortest_path_length(subgraph, source=key).values() print('{}: {} -      ' .format(famous_players[key], sum(paths) / len(paths))) 

  : 3.941461876893135 -        : 3.7971107852140182 -        : 3.89353216101753 -        : 3.8634887131481204 -        : 4.1443373857266215 -        : 3.575478680390894 -        : 3.608674497334192 -        : 4.564102739819904 -       

如果我们松开措辞，则理论得以实现-平均在4-5级熟人之间。 我们绘制了多少人直接对随机鉴赏家A. Druzem熟悉，一二三等。 鉴赏家。

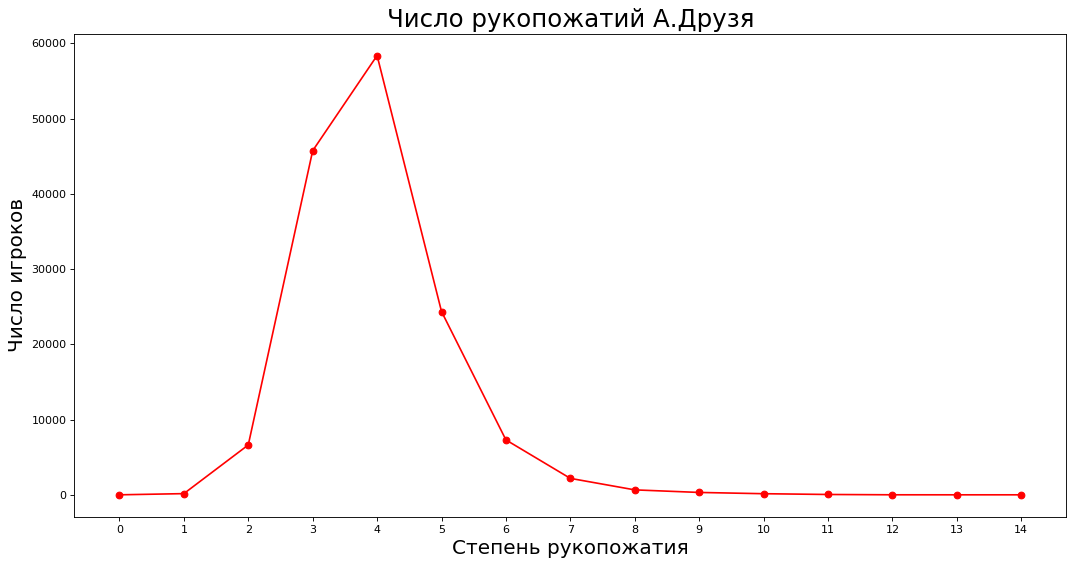
 paths = nx.shortest_path_length(subgraph, source=9808) neighbours = [0] * 15 for k in paths: neighbours[paths[k]] += 1 _count = 15 plt.figure(figsize=(16, 8), dpi=80) plt.plot(range(_count),neighbours[:_count],'ro-') # in-degree plt.xlabel(' ', fontsize=18) plt.xticks(range(_count)) plt.ylabel(' ', fontsize=18) plt.title('  .', fontsize=22) plt.show() 

在X轴上，与A. Druzem的相识程度（直接地通过一个，两个等）在Y轴上，以这种方式熟悉A. Druzem的专家的数量。

社会图

因为 为将近20万人绘制图表不是一个好主意，我们将使其变得更容易：我们将构建Kerch连通性组件以及与作者相关的人员图表。

刻赤成分

 little_v = list(sorted(nx.connected_components(G), key=len, reverse=True)[1]) little = G.subgraph(little_v) plt.figure(figsize=(24, 12), dpi=200) pos = nx.kamada_kawai_layout(little) nx.draw(little, pos=pos, node_size=100, edge_color='gray', node_color=[val for (node, val) in little.degree()], cmap=plt.cm.jet) plt.show() 

您可以看到将组件分为团队。 此外，团队通常在一个或两个社交鉴赏家的帮助下相互联系。 在中心，是与许多其他玩家一起玩耍的专家的核心。

一个人的数量

我们将找到一个人的最亲密的熟人，并查看它们之间的关系。 为了简化图表，我们不会添加该人本人（他已经与每个人建立了联系）

 id = 118622 ego_graph = [n for n in G.neighbors(id)] #ego_graph.append(id) ego_graph = G.subgraph(ego_graph) plt.figure(figsize=(24, 16), dpi=200) pos = nx.kamada_kawai_layout(ego_graph) nx.draw(ego_graph, pos=pos, node_size=100, edge_color='gray', node_color=[val for (node, val) in ego_graph.degree()], cmap=plt.cm.jet) plt.show() 

该图更加密集，可以区分10-15个人的核心。 最大点击大小为13。

结论

• 相较于社交网络，要认识体育ChGK的人要困难得多，您需要离线并至少参加一场比赛。 同时，专家遍布全球。 但是，专家之间的平均距离确实小于5。
• 评级网站使用Snyatkovsky编号 ，该编号与ChGK世界中的Erdös编号类似。 Snyatkovsky先生本人在我们最友善的鉴赏家排名中位居第三。
• 来自我github中一篇文章的代码。
• 提出宝贵意见，作者对《白噪声》和《陷害罗杰·费德勒》，米哈伊尔·阿库洛夫，薇拉·捷伦蒂耶娃和《 火月》表示感谢 。