大家好！ 新年假期即将结束，这意味着我们再次准备与您共享有用的材料。 预期将在“开发人员算法”课程上推出新的课程，因此准备了本文的翻译。
走吧
误差的反向传播方法可能是神经网络的最基本组成部分。 它最早是在1960年代描述的，近30年后，它在Rumelhart，Hinton和Williams的题为
“通过反向传播的错误学习表示法”中得到了推广。
该方法用于使用所谓的链规则（复杂函数的微分规则）有效地训练神经网络。 简而言之，在每次通过网络后，反向传播都会沿相反方向执行一次传递，并调整模型参数（权重和位移）。
在本文中，我想从数学的角度详细考虑学习和优化简单的4层神经网络的过程。 我相信这将有助于读者了解反向传播的工作原理，并了解其重要性。
定义神经网络模型
四层神经网络由输入层中的四个神经元，隐藏层中的四个神经元和输出层中的1个神经元组成。
四层神经网络的简单图像。输入层
在图中，紫色神经元代表输入。 它们可以是简单的标量，也可以是更复杂的-向量或多维矩阵。
描述输入xi的方程式。第一组激活（a）等于输入值。 “激活”是应用激活功能后神经元的值。 有关更多详细信息，请参见下文。
隐藏层
隐藏的神经元的最终值（绿色图中）是使用z
l -I层中的加权输入和L层中的
I激活来计算的。对于第2层和第3层，等式如下：
对于l = 2：
对于l = 3：
W
2和W
3是第2层和第3层的权重，b
2和b
3是这些层的偏移量。
使用激活函数f计算激活a
2和a
3 。 例如，此函数f是非线性的（如
Sigmoid ，
ReLU和
双曲正切 ），并允许网络研究数据中的复杂模式。 我们不会讨论激活功能的工作原理，但是如果您有兴趣，我强烈建议您阅读这篇精彩的
文章 。
如果仔细观察，您会发现所有x，z
2 ，a
2 ，z
3 ，a
3 ，W
1 ，W
2 ，b
1和b
2都没有四层神经网络图中所示的下标。 事实是我们将所有参数值组合到按层分组的矩阵中。 这是使用神经网络的一种标准方法，并且非常舒适。 但是，我将仔细研究方程式，以免造成混淆。
让我们以第2层及其参数为例。 可以将相同的操作应用于神经网络的任何层。
W
1是维数
（n，m）的权重矩阵，其中
n是输出神经元的数量（下一层的神经元），
m是输入神经元的数量（上一层的神经元）。 在我们的情况下，
n = 2和
m = 4 。
在这里，任何权重的下标中的第一个数字对应于下一层的神经元索引（在我们的情况下，这是第二个隐藏层），第二个数字对应于上一层的神经元索引（在我们的情况下，这是输入层）。
x是维度（
m ，1）的输入向量，其中
m是输入神经元的数量。 在我们的情况下，
m = 4。
b
1是维度（
n ，1）的位移向量，其中
n是当前层中神经元的数量。 在我们的例子中，
n = 2。
按照z
2的等式
，我们可以使用W
1 ，x和b
1的上述定义来获得等式z
2 ：
现在，请仔细看一下上面的神经网络的图示：
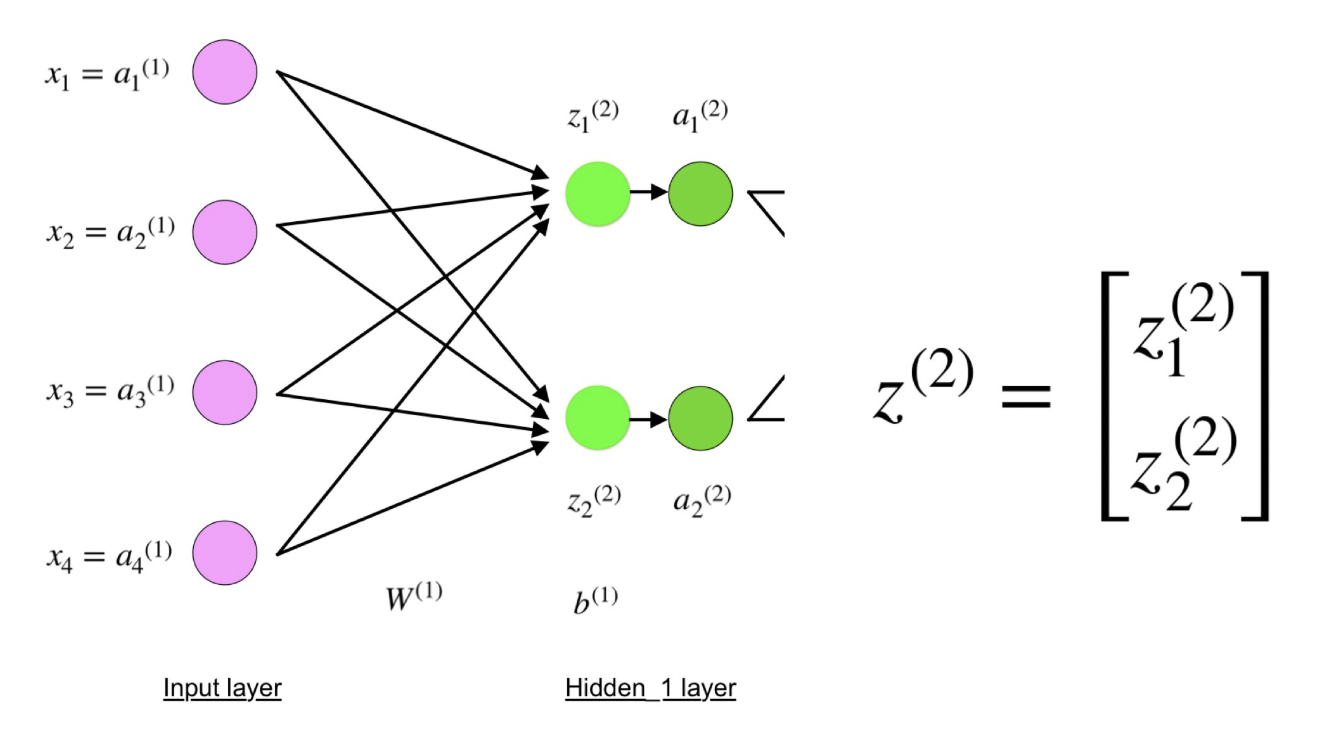
如您所见，z
2可以用z
1 2和z
2 2表示 ，其中z
1 2和z
2 2是每个输入值x
i与相应权重W
ij 1的乘积之和。
这导致z
2的方程式相同，并证明矩阵表示z
2 ，a
2 ，z
3和a
3是正确的。
输出层
神经网络的最后一部分是输出层，它给出了预测值。 在我们的简单示例中，它以染成蓝色的单个神经元的形式表示，并计算如下：
同样，我们使用矩阵表示法简化方程。 您可以使用上述方法来了解基本逻辑。
直接分发和评估
以上等式通过神经网络形成直接分布。 快速概述：
（1）-输入层
（2）-第一个隐藏层中神经元的值
（3）-第一个隐藏层上的激活值
（4）-第二个隐藏层中神经元的值
（5）-第二隐藏级别的激活值
（6）-输出层直接通过的最后一步是相对于预期输出值
y评估预测输出值
s 。
输出y是训练数据集（x，y）的一部分，其中
x是输入（如上一节所述）。
s和
y之间
的估计是通过损失函数进行的。 它可以简单地作为
标准误差 ，也可以复杂地作为
交叉熵 。
我们将此损失函数称为C并表示如下：
其中
成本可以等于标准误差，交叉熵或任何其他损失函数。
基于C的值，模型“知道”需要调整多少参数才能接近
y的预期输出值。 使用反向传播方法会发生这种情况。
误差的反向传播和梯度计算
根据1989年的文章，反向传播方法：
不断调整网络中连接的权重，以最小化网络的实际输出矢量和所需输出矢量之间的差异 。
和
...使创建有用的新功能成为可能，从而将反向传播与较早和较简单的方法区分开...换句话说，反向传播旨在通过调整网络的权重和偏移来使损耗函数最小化。 调整程度由损耗函数相对于这些参数的梯度确定。
一个问题出现了：
为什么要计算梯度 ？
要回答这个问题，我们首先需要修改一些计算概念：
函数C（x
1 ，x
2 ，...，x
m ）在x处的
梯度是 C
相对于
x 的偏导数的
向量 。
函数C的导数反映了相对于函数自变量
x （
输入值 ）变化对函数值（输出值）变化的敏感性。 换句话说，导数告诉我们C.向哪个方向移动。
梯度表示为了最小化C，有必要改变参数
x （在正方向或负方向上）多少。
这些梯度是使用称为链
规则的方法计算的。
对于一个权重（w
jk ）
l，梯度为：
（1）连锁规则
（2）根据定义，m是每l-1层的神经元数量
（3）导数计算
（4）最终价值
可以将一组相似的方程式应用于（b j ） l ：
（1）连锁规则
（2）导数计算
（3）最终价值这两个方程的共同部分通常称为“局部梯度”，其表示如下：
使用链式规则可以轻松确定“局部梯度”。 我现在不会画这个过程。
渐变允许优化模型参数：
在达到停止标准之前，将执行以下操作：
优化权重和偏移量的算法 （也称为梯度下降）
- w和b的初始值是随机选择的。
- Epsilon（e）是学习的速度。 它确定渐变的效果。
- w和b是权重和偏移量的矩阵表示。
- C关于w或b的导数可以使用C关于各个权重或偏移的偏导数来计算。
- 一旦损失函数最小化，则满足终止条件。
我想将本节的最后部分放在一个简单的示例中，在该示例中，我们针对一个权重（w
22 ）
2计算梯度C。
让我们放大上述神经网络的底部：
神经网络中反向传播的可视化表示权重（w
22 ）
2连接（a
2 ）
2和（z
2 ）
2 ，因此计算梯度需要在（z
2 ）
3和（a
2 ）
3上应用链式规则：
从（a
2 ）
3计算C的导数的最终值需要了解函数C。由于C取决于（a
2 ）
3 ，所以导数的计算应该很简单。
我希望这个例子能够对计算梯度的数学原理有所启发。 如果您想了解更多信息，我强烈建议您阅读Stanford NLP系列文章，Richard Socher为其中的反向传播提供了4种出色的解释。
结束语
在本文中，我详细说明了如何使用数学方法（例如计算梯度，链规则等）在后台进行错误的反向传播。 了解该算法的机制将增强您对神经网络的了解，并让您在使用更复杂的模型时感到自在。 祝您在深度学习过程中一切顺利！
仅此而已。 我们邀请所有人参加主题为“细分树：简单快速”的免费网络研讨会。