前几章

30.学习曲线解释：大偏差

假设您在验证样本上的误差曲线如下所示：

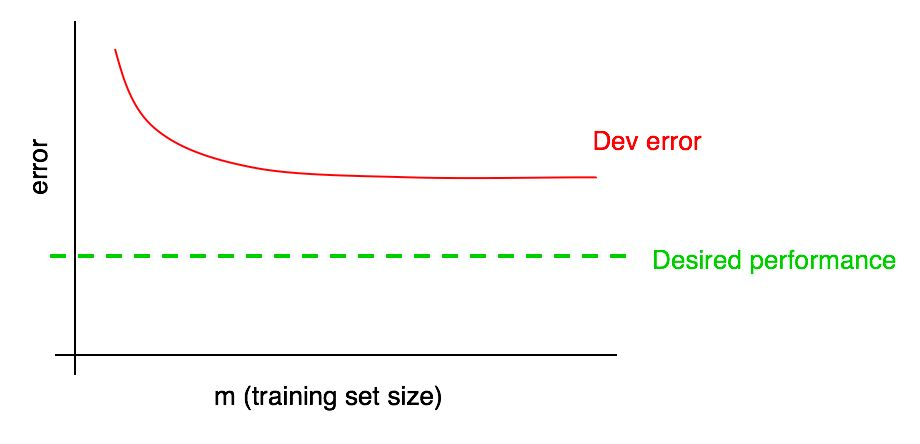
我们已经说过，如果验证样本中的算法错误达到平稳状态，那么仅通过添加数据就不可能达到所需的质量水平。

但是很难想象添加数据时算法质量对验证样本的依赖关系的曲线外推（Dev误差）会是什么样子。 而且，如果验证样本很小，则由于曲线可能存在噪声（点分布较大），因此回答该问题会更加困难。

假设我们在图中添加了误差幅度与测试样本数据量的关系曲线，并得到了以下图片：

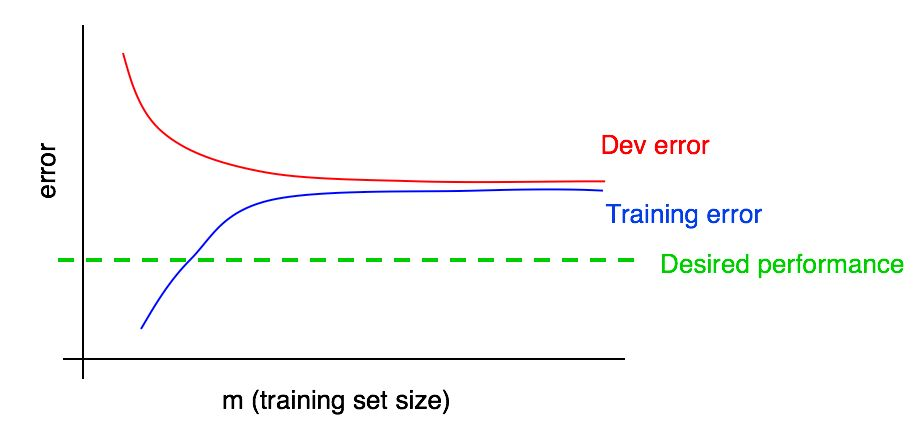
通过查看这两条曲线，您可以绝对确定仅添加新数据不会达到预期的效果（这不会提高算法的质量）。 在哪里可以得出这个结论？
让我们回顾以下两点：

• 如果我们将更多数据添加到训练集中，则训练集中的算法错误只会增加。 因此，图表的蓝线不会改变，或者会爬升，并且会偏离算法的期望质量水平（绿线）。
• 验证样本中的红色误差线通常高于训练样本中算法的蓝色误差线。 因此，在任何可能的情况下，添加数据都不会导致红线进一步减少，也不会使其接近所需的错误级别。 考虑到即使训练样本中的误差也高于期望值，这几乎是不可能的。

考虑到算法误差与验证图上的数据量和训练图上的数据量的依赖关系的两条曲线，可以使您更自信地从验证样本中的数据量推断学习算法的误差曲线。

假设我们以系统中最佳错误级别的形式对算法的期望质量进行了估算。 在这种情况下，以上图表说明了标准“教科书”情况，即学习曲线在高水平可移动偏见下的外观。 在最大的训练样本大小（大概对应于我们掌握的所有数据）的情况下，训练样本中的算法错误与算法的期望质量之间存在较大的差距，这表明可以避免较高的偏差。 另外，训练样本中的误差与验证样本中的误差之间的差距很小，这表明分布很小。

之前，我们仅在图形上方的最右边讨论了在训练和验证样本上训练的算法的错误，这与使用我们拥有的所有训练数据相对应。 针对用于训练的样本的不同大小构造的误差对训练样本的数据量的依赖性曲线为我们提供了对在不同大小的训练样本上训练的算法的质量的更完整描述。

31.学习曲线解释：其他情况

考虑学习曲线：

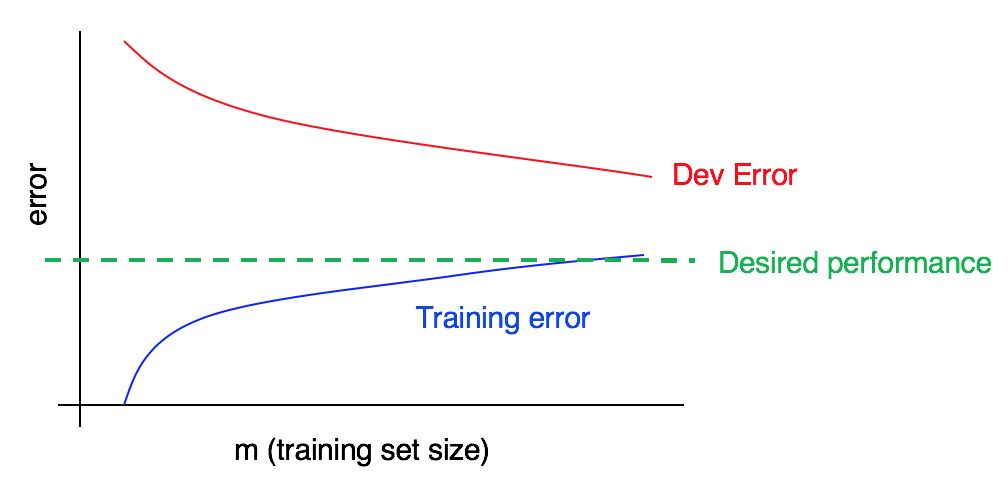
是否存在高偏差或高解析度，或同时存在？

训练数据上的蓝色误差曲线相对较低，验证数据上的红色误差曲线明显高于训练数据上的蓝色误差。 因此，在这种情况下，偏差很小，但是展宽很大。 添加更多的训练数据可能有助于缩小验证样本中的错误和训练样本中的错误之间的差距。

现在考虑以下图表：

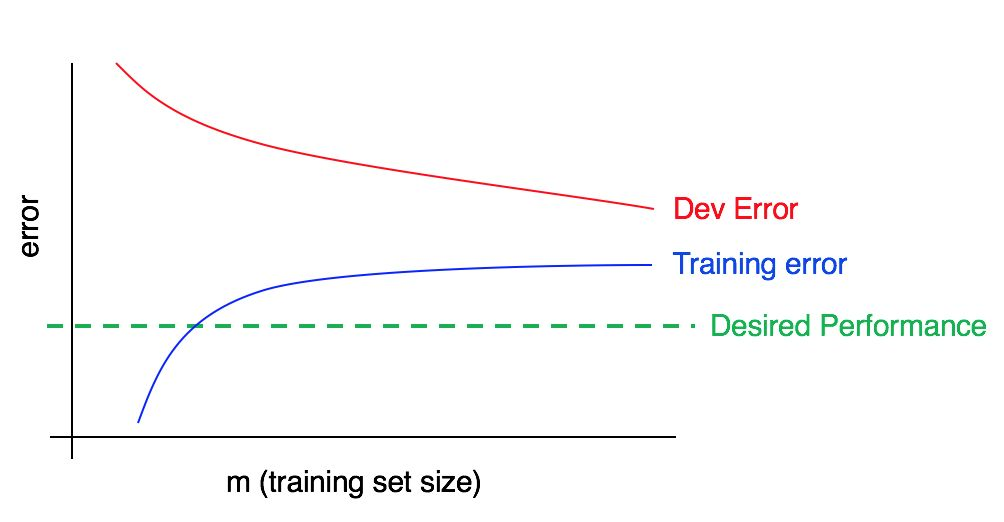
在这种情况下，训练样本中的误差很大；它明显高于对应于所需质量水平的算法。 验证样本中的误差也大大高于训练样本中的误差。 因此，我们正在同时处理较大的偏差和分散。 您应该寻找减少，抵消和分散算法的方法。

32.建立学习曲线

假设您有一个非常小的培训样本，仅包含100个示例。 您使用10个示例的随机选择子集训练算法，然后从20个示例中选择，然后从30个中依次类推到100，从而以10个示例为间隔增加示例数量。 然后使用这10点来建立学习曲线。 您可能会发现，对于较小的训练样本，该曲线看起来很嘈杂（值高于或低于预期）。

当仅使用10个随机选择的示例来训练算法时，可能不会很幸运，这会成为特别“不好”的训练子样本，其中包含较多的歧义/错误标记的示例。 或者相反，您可能会遇到一个特别“不错”的训练子样本。 一个小的训练样本的存在意味着验证和训练样本中的误差值可能会受到随机波动的影响。

如果用于使用机器学习的应用程序的数据严重偏向一类（例如，在cat分类问题中，否定示例的比例远大于肯定示例的比例），或者我们正在处理大量类（例如识别100种不同动物的物种），那么获得特别“代表性不足”或训练不佳的样本的机会也会增加。 例如，如果您的示例中有80％是负面示例（y = 0），而只有20％是正面示例（y = 1），则很有可能10个示例的训练子集将仅包含负面示例，在这种情况下从经过训练的算法中很难获得合理的信息。

如果由于训练样本中学习曲线的嘈杂而难以评估趋势，则可以提出以下两种解决方案：

• 代替只为10个训练示例训练一个模型，而是从包含100个示例的初始样本中替换选择几个（例如3到10个）不同的随机训练子样本。 在每个模型上训练模型，并为每个模型计算验证和训练样本上的误差。 在训练和验证样本上计算并绘制平均误差。

  
  

  作者的评论： 带有替换示例的样本意味着：从100个样本中随机选择前10个不同样本，以形成第一个训练子样本。 然后，要形成第二个训练子样本，请再次再次使用10个示例，但要排除在第一个子样本中选择的那些（再从一百个示例中选择）。 因此，两个子样本中都可能出现一个特定示例。 这将有替换样本与无替换样本区分开来，在无替换样本的情况下，仅从不属于第一个子样本的90个示例中选择第二个训练子样本。 实际上，选择带有或不带有替换的示例的方法应该不是很重要，但是带有替换的示例的选择是很常见的做法。

  
  

• 如果您的训练样本偏向某一类别，或者如果它包含许多类别，请选择“平衡”子样本，该子样本由10个训练样本组成，并从100个样本样本中随机选择。 例如，您可以确定2/10个示例为正，8/10个为负。 总而言之，您可以确保观察到的数据集中每个类别的示例所占的比例与初始训练样本中所占的比例尽可能接近。

  
  

  我不会理会这些方法中的任何一种，除非绘制误差曲线的图形得出结论，即这些曲线过于嘈杂，这使我们无法看到可理解的趋势。 如果您有大量的培训样本-假设有大约10,000个示例，并且您的课程分布不是很偏重，则可能不需要这些方法。

  
  

最后，从计算的角度来看，建立学习曲线可能会很昂贵：例如，您需要训练十个模型，在前1000个示例中，在第二个2000中，依此类推，直到最后一个包含10,000个示例的模型。 对少量数据进行模型训练要比对大样本进行模型训练要快得多。 因此，您可以像上面描述的那样（1000、2000、3000，...，10000）沿线性比例均匀分布训练子样本的大小，而可以训练样本数量非线性增加的模型，例如1000、2000、4000、6000和10,000个示例。 一样，它应该使您清楚地了解模型质量对学习曲线中训练示例数量的依赖性趋势。 当然，仅当训练附加模型的计算成本很高时，此技术才有意义。

延续