🏝️ 🙍🏽 👆🏾 混合排序 🧚 📣 🆑

众所周知，排序可以基于交换，插入，选择，合并和分发。

但是，如果在算法中组合了不同的方法，则它属于混合排序类别。

本文是在EDISON的支持下编写的。

我们从事1C-Bitrix上站点的完成和维护，以及Android和iOS移动应用程序的开发。

我们喜欢算法理论！ ;-)

让我们快速回顾一下排序算法具有哪些类，以及它们各自的功能。

交换排序

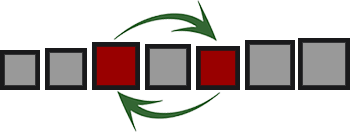
数组中的元素彼此成对比较，并进行无序对交换。

这个班上最有效的代表是传说中的快速排序 。

插入排序

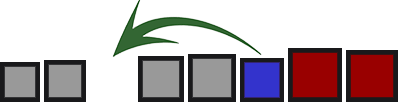
来自数组未排序部分的元素将插入到其在排序区域中的位置。

在此类中，最常用的是通过简单插入进行排序 。尽管此算法的平均复杂度为O（ n ² ），但这种排序对几乎有序的数组非常有效-复杂度达到O（ n ）。此外，这种排序是处理小型阵列的最佳选择之一。

使用二叉搜索树排序也属于此类。

按选择排序

在无序区域中，选择了最小/最大元素，该元素被传送到数组未排序部分的末尾/开始。

使用简单选择进行排序的过程非常缓慢（平均为O（ n ² ）），但是在此类中， 通过堆进行 排序（又称为金字塔排序 ）非常困难，时间复杂度为O（ n log n ）-这非常有价值，无论输入数据如何，都不会发生这种分类的退化情况。顺便说一句，这种分类也不是输入数据的最佳情况。

合并排序

将已排序的区域放入数组中，然后将它们合并，即，将较小的已排序子数组合并为较大的已排序子数组。

如果对两个子数组进行了排序，则将它们组合起来将是易于实现且快速的操作。硬币的另一面是，合并几乎总是需要额外的内存成本O（ n ）-尽管很少有非常复杂的选项用于合并排序，而内存成本为O（1）。

按分布排序

数组的元素被分发并重新分发到类中，直到该数组接受排序状态为止。

根据元素的值（所谓的计数排序 ）或根据单个数字的值（这些已经是按位排序 ）将元素分为几组。

桶分类也属于此类。

按分布排序的特征是它们要么不使用元素之间的成对比较，要么这种比较很小。因此，按分布排序通常比速度快，例如快速排序。另一方面，按分布排序通常需要大量额外的内存，因为需要将一组不断重新分布的元素存储在某个位置。

关于哪种排序最好的争论非常频繁，但是事实是，没有而且不可能在所有情况下都存在理想的算法。例如，在大多数情况下，快速排序确实非常快（但不是最快），但是在发生崩溃的退化情况下也可能遇到这种情况。通过简单的插入进行排序很慢，但是对于几乎有序的数组，它将很容易绕过其他算法。堆排序对任何传入数据都非常快，但是在某些条件下不如其他排序快，并且无法加快金字塔传输的速度。合并排序比快速排序慢，但是，如果数组中有已排序的子数组，则合并它们比通过快速排序进行排序要快。如果数组包含许多重复元素，或者我们对行进行了排序，那么最有可能按分布进行排序是最佳选择。每种方法在最有利的情况下特别好。

尽管如此，程序员继续发明世界上最快的排序方法，综合了不同类中最有效的方法。让我们看看对他们来说有多成功。

由于在本文中提到了许多非平凡的算法，因此我仅简要介绍其工作的基本原理，而不会在本文中增加动画和详细说明。将来会有单独的文章，每种算法都会有卡通插图，并会细化细微差别。

插入+合并

纯粹凭经验得出的结论是，融合和/或插入最常用于杂种中。在大多数排序中，都会找到一种或另一种方法，或者两者都在一起。对此有一个合乎逻辑的解释。

排序发明人通常努力创建并行算法，以同时对数组的不同部分进行排序。处理几个排序的子数组的最好方法是将它们合并-这将是最快的。

现代算法经常使用递归。在递归下降过程中，通常将数组分为两部分；在最低级别上，对数组进行排序。当返回较高级别的递归时，出现的问题是合并以较低级别排序的子数组。

至于插入物，在某些阶段的混合算法中，通常会获得近似有序的子阵列，最好在插入物的帮助下导致最终排序。

该组包含混合排序，其中存在合并和插入，并且这些方法的用法非常不同。

合并插入排序
福特约翰逊算法::福特约翰逊算法

合并+插入

一种非常古老的方式，早在1959年。在Donald Knuth的不朽著作中，“编程的艺术”，第3卷，“排序和搜索”，第5章，“排序”，第5.3节，“最佳排序”，第5.3节，“按最小比较数排序”，以及“通过插入和合并排序”部分对此进行了详细描述。。

排序现在没有实际价值，但是对于那些热爱算法理论的人来说很有趣。考虑了寻找一种以最少数量的比较来对n个元素进行排序的方法的问题。提出了一个非平凡的启发式修改，用于使用Jacobstal数对插入进行排序（这种插入在其他地方都找不到），以最大程度地减少比较次数。迄今为止，众所周知这不是最好的选择，您甚至可以更巧妙地躲避并获得更少的比较。通常，标准的学术排序并没有实际用途，但是对于该类型的鉴赏家来说，很高兴以代数偏向分解此类技巧。

蒂姆·索特::蒂姆索特

插入+合并

Tim Peters发表于15年前

人们经常记得在哈布雷（Habré）上进行这种排序。
命题：在一个数组中，搜索几乎有序的小子数组，以了解使用了插入排序。然后使用合并将这些子数组合并。

TimSort中的合并是最有趣的部分：经典的向上合并针对不同情况进行了进一步优化。例如，已知如果所连接的子阵列的大小大致相同，则合并更有效。在TimSort中，如果大小相差很大，则在执行其他操作后会进行调整（可以说部分元素将从较大的子数组“流”到较小的子数组，然后合并将以标准模式继续）。还提供了各种隐患情况-例如，如果一个子数组中的所有元素都少于另一个子数组中的所有元素。在这种情况下，来自两个子阵列的元素的比较将是空闲的。修改后的合并程序将“注意到”事件的这种不良发展，如果使用二进制搜索“确信”悲观的选择，它将切换到更优化的处理选项。

平均而言，这种排序比QuickSort慢一点，但是，如果传入数组包含足够数量的元素的有序子序列，则速度会显着提高，并且TimSort会领先于其余排序。

块合并排序::块合并排序
Wiki-sort :: Wiki-sort
圣杯排序:: Grailsort

插入+合并+桶

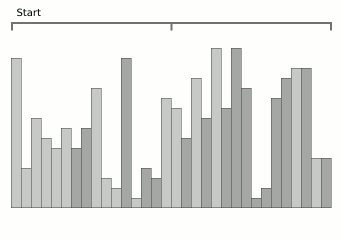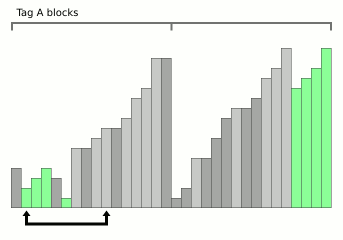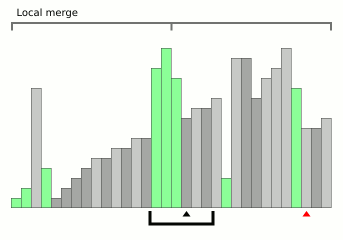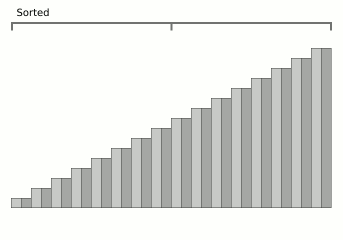Wikipedia中的块合并排序动画。

这是一个非常新颖的算法（2008年），同时也是非常有前途的算法。事实是，合并的相对重要的问题是附加内存的成本。通常，在有合并的地方，内存复杂度也为O（ n ）。

但是WikiSort的设计宗旨是在不使用额外内存的情况下进行合并-在合并排序中，就此而言，这是非常罕见的实例。另外，该算法是稳定的。好吧，如果常规合并排序具有最佳算法速度O（ n log n ），那么在Wiki排序中，此指标为O（ n ）。直到最近，人们还认为原则上不可能将具有这种特征的排序合并在一起，但是中国程序员对此感到惊讶。

该算法很难用几个句子来解释。但是总有一天，我会为他写一个单独的狂欢。

最初，该算法被无名地称为Block Merge Sort，但是在Tim Peters的帮助下，他详细研究了排序（以确定是否应将其某些思想转移到TimSort），这个名字就是WikiSort。

不合时宜的habruiser Mrrl独立地工作了几年，进行合并排序，这将与任何传入的数据同时快速，内存经济且稳定。他的创造性搜索很成功，后来他称开发的算法为“圣杯”的分类（因为它满足了“完美分类”的所有高要求）。该算法的大多数思想与WikiSort中实现的思想相似，尽管这些类型并不相同并且彼此独立地开发。

哈希表排序::哈希表排序

分发+插入+合并

将该数组递归地分成两部分，直到结果子数组中的元素数量达到某个阈值为止。在最低的递归级别上，将发生近似分布（使用哈希表），并且子数组按插入顺序排序。然后递归返回更高的级别，将合并的两半合并在一起。

一个月前，我进一步讨论了该算法。

快速排序为主要

合并并插入后，每个人都喜欢的快速排序牢固地将其置于混合命中游行中的第三位。

这是一种非常有效的算法，但也有退化的情况。一些发明者试图使QuickSort完全不受任何不良输入数据的影响，并建议用其他类型的强力思想对其进行补充。

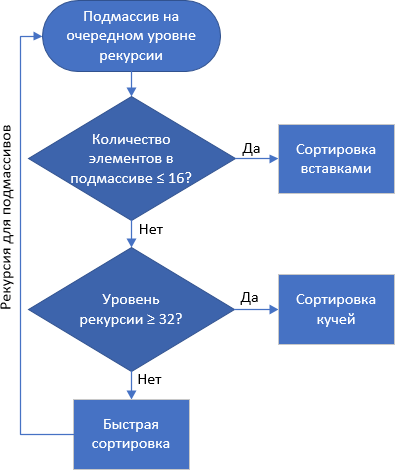
内省排序:: Introsort，内省排序，std ::排序

快速+堆+插入

堆排序比快速排序要慢一些，但与此同时，与QuickSort不同，堆排序没有退化的情况-平均，最佳和最差算法时间复杂度为O（ n log n ）。

因此，大卫·穆瑟（David Musser）提出在快速分拣过程中是安全的-如果嵌套过多，则这被视为对系统的攻击，从而造成了“不良”阵列。切换到按堆排序会发生，这不是兆字节，但处理任何传入数据也不慢。

C ++有一种称为std :: sort的算法，它是自省排序的一种实现。一个小的加法-如果在下一递归级别上，子数组的元素数≤16 ，则将插入排序应用于子数组。

多键排序::多键排序
按位快速排序::基数快速排序

快速+排名

快速排序时，仅将数组元素的值相互比较，但将它们的单个数字进行比较（首先，我们以这种方式对较高的数字进行排序，从最低的数字开始进行排序）。

大概-这是高位按位排序，下一位内部的排序是根据快速排序算法执行的。

散点图:: Spreadsort

快速+合并+桶+排放

快速排序，合并排序，存储桶排序和按位排序的格式塔。

简而言之，不解释。我们将在以下文章之一中详细分析此算法。

其他杂种

树数排序

计数+树

用户AlexanderUsatov 提出的算法。计数排序，计数的键数存储在平衡树中。

J-sort :: J-sort

堆+插入

5年前，我已经写过有关这种排序的文章。一切都非常简单-首先在数组中需要一次构建一个非递增堆，然后执行相反的操作-一次构建一个非递减堆。第一次操作的结果是，最小值将位于数组的第一位，而小的元素整体将明显移至开头。在第二种情况下，最大值将排在最后，大型元素将移向数组的末尾。总的来说，我们得到一个几乎排序的数组，我们用它做什么？没错-整理插入内容。