一篇有趣的经文的翻译，致力于信息理论中概念的可视化。 在第一部分中，我们将研究如何以图形方式表示概率分布，它们之间的相互作用以及条件概率。 接下来，我们将处理固定长度和可变长度的代码，了解如何构建最佳代码以及为什么这样做。 作为补充，可以从视觉上理解辛普森统计悖论。信息论为我们提供了一种描述许多事物的准确语言。 我有多少不确定性？ 关于问题A的答案有多少知识告诉我有关问题B的答案？ 一套信念与另一套信念有多相似？ 当我还是个孩子的时候，我有这些想法的非正式版本，但是信息理论将它们具体化为精确而有力的想法。 这些想法具有广泛的应用，从数据压缩到量子物理学，机器学习以及它们之间的广阔领域。
不幸的是，信息理论似乎令人生畏。 我认为没有任何原因。 实际上，许多关键思想可以用视觉方式解释！
概率分布可视化
在深入研究信息理论之前，让我们考虑一下如何可视化简单的概率分布。 以后我们将需要它们，此外，这些用于可视化概率的技术本身很有用！
我在加利福尼亚。 有时会下雨，但主要是阳光！ 假设有75％的时间是晴天。 在图中很容易描绘：
大多数时候，我穿T恤，但有时我穿雨衣。 假设我有38％的时间穿雨衣。 这也很容易描绘。
如果我想同时可视化两个事实怎么办？ 如果他们不互动，那就很简单-即 是独立的。 例如，如果这样：今天我穿T恤或雨衣并不取决于下周的天气。 我们可以使用一个轴代表一个变量，而另一个代表另一个：
注意贯穿直线的垂直和水平线。 这就是独立的样子！ 由于一周会下雨，我穿雨衣的可能性不会改变。 换句话说，我将穿雨衣且下周下雨的概率等于我将穿雨衣的概率乘以下雨的概率。 他们不互动。
当变量相互作用时，某些变量对的概率可能会增加，而另一些变量对的概率可能会降低。 我穿雨衣和下雨的可能性很高，因为变量之间存在相关性，它们之间的相互影响更大。 与下一天有雨衣而又有一天下雨的可能性相比，下雨天我穿雨衣的可能性更大。
从视觉上看，似乎某些方格以其他概率膨胀，而其他方格变窄，因为几个事件不太可能同时发生：
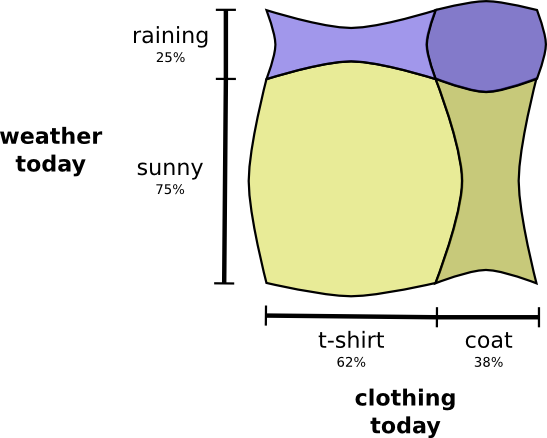
但是，尽管它看起来很酷，但是对于了解正在发生的事情并不是很有用。
取而代之，让我们关注像天气这样的变量。 我们知道晴天和阴雨天气的可能性。 在这两种情况下，我们都可以考虑条件概率。 如果晴天，我穿T恤的可能性有多大？ 如果下雨，我穿雨衣的可能性是多少？
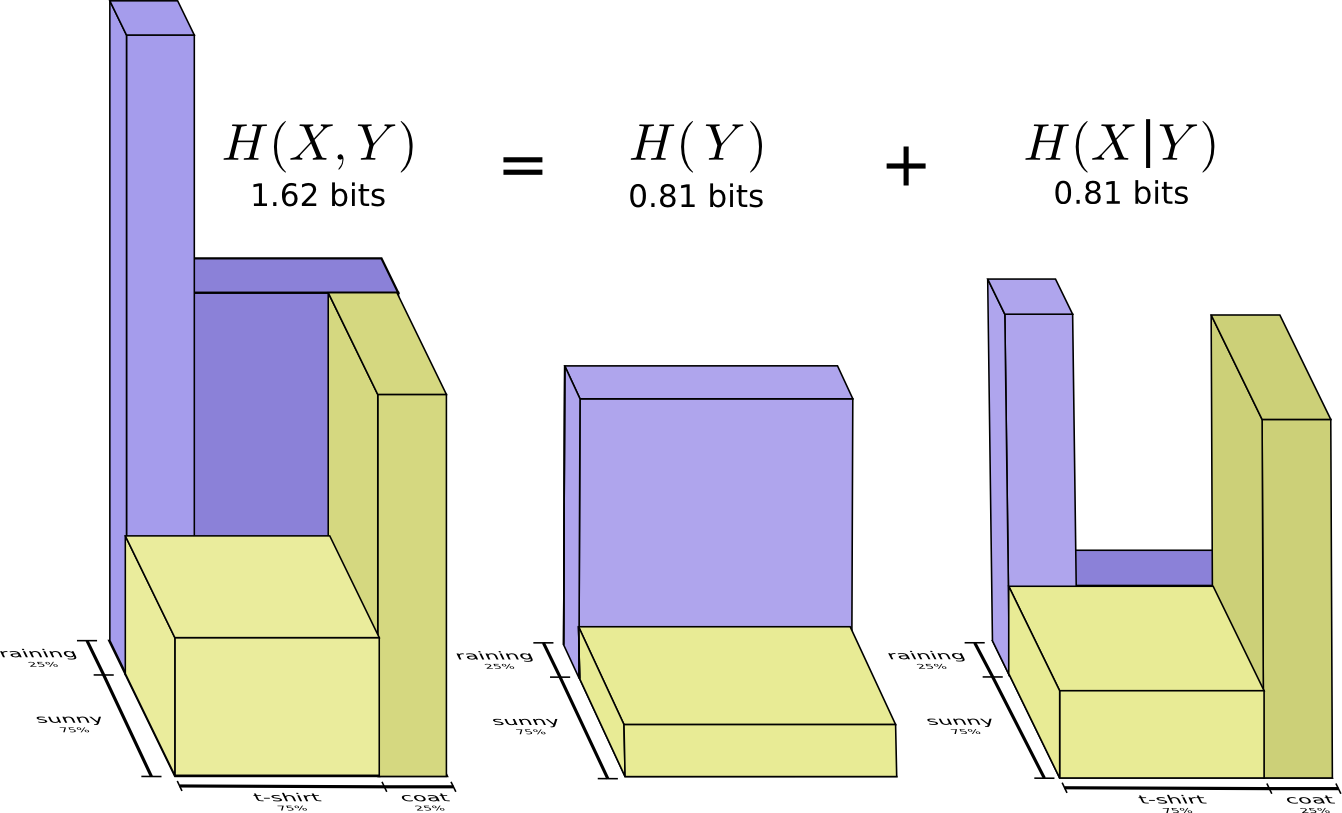
很有可能会下雨25％。 如果下雨，我会穿雨衣的几率为75％。 因此，下雨和我穿雨衣的可能性是75％的25％，大约是19％。 下雨的概率并且我穿着雨衣是下雨的概率乘以如果下雨我会穿雨衣的概率。 我们这样写：
这是概率论最基本身份之一的一个例子：
我们通过将分销分成两部分来考虑分销。 首先，我们看一下天气等变量取某个值的可能性。 然后，我们看一下另一个变量（我的衣服）由于第一个变量而具有该值的可能性。
以哪个变量开头并不重要。 我们可以从我的衣服开始，然后看看由此引起的天气。 这似乎不太直观，因为我们知道天气之间存在因果关系，这会影响我的穿着，反之亦然……但反正仍然有效！
让我们来看一个例子。 如果我们选择随机的一天，则有38％的可能性我会穿雨衣。 如果我们知道我穿着雨衣，下雨的可能性有多大？ 我宁愿在雨中穿雨衣，也不愿在阳光下穿雨衣，但是加利福尼亚的雨很少见，事实证明有50％的机会会下雨。 因此，下雨的几率和我穿雨衣的几率是我将穿雨衣的几率（38％）乘以我穿雨衣的下雨的几率（50％），即约19％。
这为我们提供了可视化相同概率分布的第二种方法。
请注意，标签值与上图中的含义略有不同：现在是T恤和雨衣的极限概率，这是我在不考虑天气的情况下穿这些衣服的概率。 另一方面，现在有两个雨痕和太阳痕，因为它们的概率取决于我将穿T恤或雨衣的事实。
（您可能听说过贝叶斯定理。您可以将其想象为这两种表示概率分布的不同方式之间的过渡方式！）
方框：辛普森悖论
这些用于概率分布的可视化技术真的有用吗？ 我认为是！ 再进一步，我们使用它们来可视化信息理论，但是现在我们使用它们来研究辛普森悖论。 辛普森悖论是一种非常不直观的统计情况。 在直觉上很难理解。 迈克尔·尼尔森（Michael Nielsen）写了一篇出色的论文《
重塑解释》 ，从许多方面解释了这一悖论。 我想尝试使用上一节中开发的技术自己做。
正在测试两种治疗肾结石的方法。 一半的患者接受治疗A，另一半接受治疗B。接受治疗B的患者比接受治疗A的患者更有可能康复。
但是，肾小结石的患者接受治疗A更有可能康复。肾脏大肾结石的患者接受治疗A也更有可能康复！ 怎么会这样
问题的实质是研究没有适当地随机化。 在接受治疗A的患者中，有大肾结石的患者更多，而接受治疗B的患者中，有小肾结石的患者更多。
事实证明，肾结石较小的患者通常更有可能康复。
为了更好地理解这一点，我们可以合并前面的两个图。 结果是三维图，其恢复率分为大小肾结石。
现在我们看到，无论是大块还是小块，治疗A都优于治疗B。治疗B看起来更好，仅是因为使用它的患者通常有更多的康复机会！
代号
现在我们有了可视化概率的方法，我们可以深入研究信息论。
让我告诉你我虚构的朋友鲍勃。 鲍勃非常喜欢动物。 他经常谈论动物。 实际上，他只说四个字：“狗”，“猫”，“鱼”和“鸟”。
几个星期前，尽管鲍勃（Bob）是我的幻想，但他还是搬到了澳大利亚。 另外，他决定只想以二进制格式进行通信。 我从Bob收到的所有（虚构的）消息都看起来像这样：
为了进行交流，Bob和我需要创建一个编码系统-一种以位序列显示单词的方法。
要发送消息，Bob将每个字符（单词）替换为相应的代码字，然后将它们组合在一起以形成编码字符串。
可变长度代码
不幸的是，在虚构的澳大利亚，通信服务非常昂贵。 从鲍勃那里收到的每封邮件，我都要支付5美元。 我是否提到鲍勃喜欢讲话？ 为了不破产，我和鲍勃决定找出是否有可能以某种方式减少平均消息长度。
事实证明，鲍勃并非所有单词的发音都一样。 鲍勃非常爱狗。 他一直在谈论狗。 有时他谈论其他动物-特别是他的狗喜欢追逐的猫-但大多数时候他谈论狗。 这是他说话频率的图表：
这令人鼓舞。 我们的旧代码使用2位代码字，无论使用频率如何。
有一个很好的方法可以形象地看到这一点。 在下图中，我们使用垂直轴来可视化每个单词的概率
和水平轴以可视化相应代码字的长度
。 请注意，结果区域是我们发送的代码字的平均长度，在这种情况下为2位。
我们可以变得更聪明，并使代码的长度可变，从而使常用字的代码字变短。 问题是代码字之间存在竞争-使某些字变得更短，我们被迫使其他字变得更长。 为了最小化消息的长度，理想情况下，我们希望所有代码字都较短，但是最短的应该广泛使用。 因此，生成的代码包含用于普通单词（例如“ dog”）的较短代码字和用于稀有单词（例如“ bird”）的较长代码字。
让我们再次形象化。 请注意，最常见的代码字较短，而最罕见的代码字较长。 结果，我们减小了面积。 这对应于较短的预期码字长度。 现在，平均码字长度为1.75位！
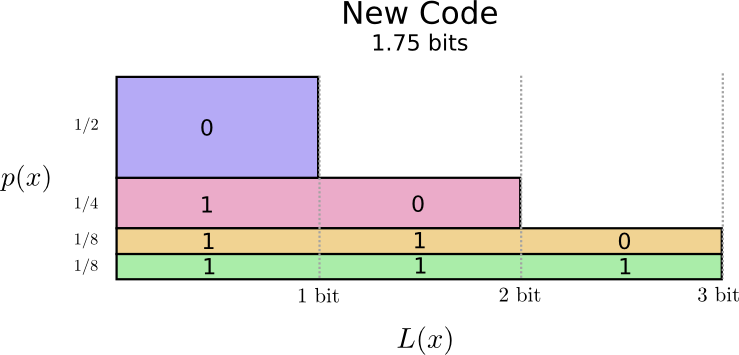
（您可能想知道：为什么不单独将1用作代码字？不幸的是，这在解码编码的字符串时会引起歧义。稍后我们将进一步讨论。）
原来，这段代码是最好的。 没有这种分配的代码可以使我们获得的平均码字长度小于1.75位。
有一个基本的限制。 所说的单词的传输，发生这种分布的事件，要求我们平均传输至少1.75位。 无论我们的代码有多聪明，都不可能实现平均消息长度更短。 我们称此基本极限为
分布熵 -我们将在下面更详细地讨论它。
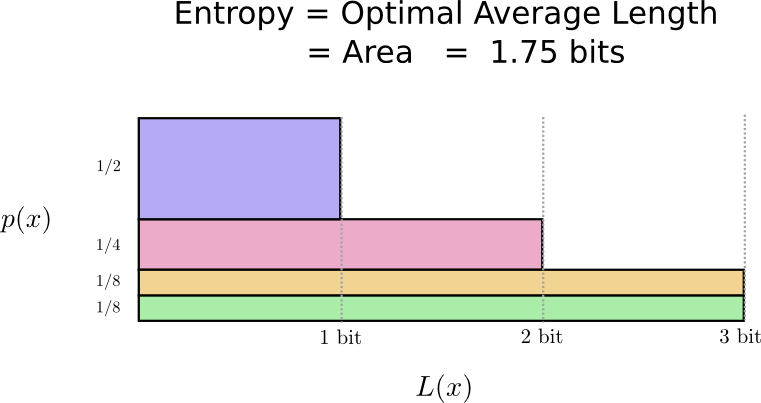
如果我们想了解此限制，则需要了解使某些代码字短而另一些代码字长之间的权衡。 一旦我们弄清楚了，就可以找出最佳的编码系统是什么样的。
码字空间
有两个长度为1位的代码字：0和1。有四个长度为2位的代码字：00、01、10和11。每增加一位，就会使可能的代码字数量加倍。
我们对可变长度代码很感兴趣，其中某些代码字比其他代码字长。 当我们有8个3位长的码字时，我们可能会遇到简单的情况。 可能存在更复杂的混合，例如，两个长度为2的代码字和四个长度为3的代码字。是什么决定了我们可以拥有多少个不同长度的代码字？
回想一下，Bob将他的消息转换为加密的字符串，用他的代码替换每个单词并将其串联。
创建可变长度代码时，有一个细微的问题要小心。 我们如何将编码后的字符串分成代码字？ 当所有代码字都具有相同的长度时，这很容易-只需将字符串分成该长度的段即可。 但是由于存在各种长度的代码字，因此我们需要注意其内容。
我们希望我们的代码具有独特的可解码性。 而且，我们不希望它在确定由哪些代码字构成编码字符串时含糊不清。 如果我们有一个特殊的符号“代码字的结尾”，那将很简单。 但是我们没有这个-我们只发送0和1。我们需要能够查看代码字的序列，并确定每个代码字的结尾。
制作无法明确解密的代码非常简单。 例如，假设0和01都是代码字。 然后不清楚0100111行的第一个代码字是什么-它可以是this或that！ 我们需要的属性是，如果我们看到一个特定的代码字，则不应将其包含在另一个较长的代码字中。 换句话说，任何代码字都不应该是另一个代码字的前缀。 这称为前缀属性，遵守该属性的代码称为
前缀代码 。
表示这种情况的一种有用方法是，每个代码字都需要牺牲可能的代码字空间。 如果采用代码字01，则将无法使用其前缀为任何代码字。 由于模棱两可，我们无法再使用010或011010110-它们已对我们丢失。
由于所有代码字的四分之一都从01开始，因此我们捐赠了所有可能代码字的四分之一。 这是我们付出的代价，以换取我们只有一个码字长度只有2位的事实！ 反过来，这种牺牲意味着所有其他代码字应稍长一些。 不同代码字的长度之间总是存在一种折衷。 简短的代码字要求您牺牲可能的代码字的大部分空间，从而避免了其他代码字的简短性。 我们需要找出的是如何正确妥协！
最佳编码
您可以将其视为有限的预算，可以花费在获取短代码字上。 我们为一个代码字付费，牺牲了部分可能的代码字。
购买长度为0的代码字的成本为1（所有可能的代码字），如果您想拥有长度为0的代码字，则不能再使用其他任何代码字。 长度为1（例如，“ 0”）的代码字的成本为1/2，因为一半可能的代码字以“ 0”开头。 长度为2的代码字（例如“ 01”）的成本为1/4，因为所有可能的代码字中有四分之一以“ 01”开头。 通常，码字的成本随着码字长度的增加而呈指数下降。
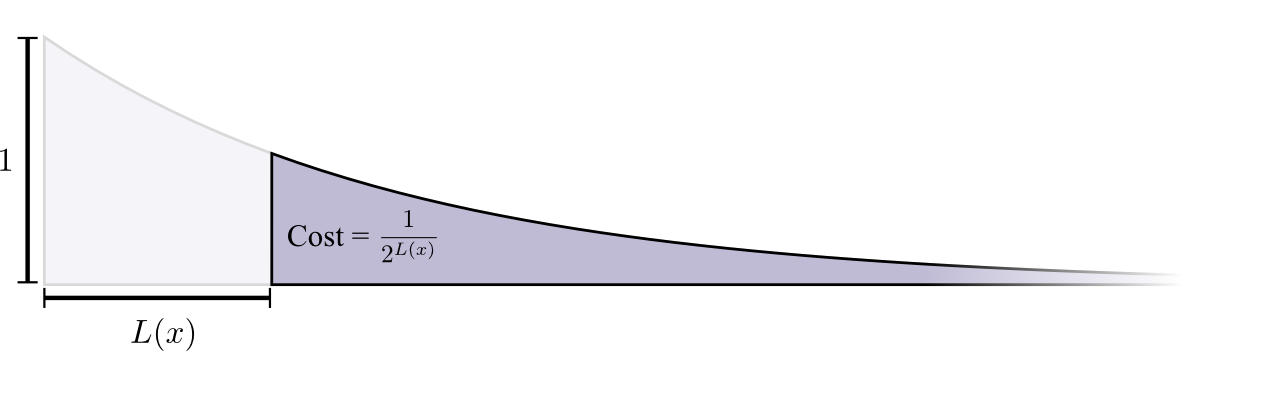
请注意，如果作为（实物）参展商的成本下降，那么这既是高度又是面积！ （
该示例使用了以2为底的指数，但事实并非如此，但是您可以切换到自然指数，从而在视觉上简化了证明。 ）
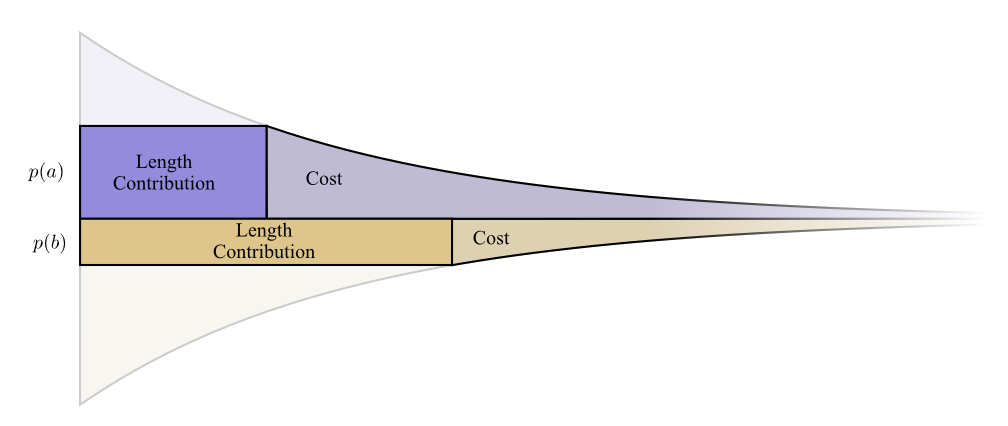
我们需要短码字，因为我们想减少平均消息长度。 每个代码字将平均消息长度增加一个字的概率乘以它的长度。 例如，如果我们需要在50％的时间中发送4位长的代码字，则平均消息长度将比不发送此代码字时长2位。 我们可以把它想象成一个矩形。
这两个值与码字长度相关。 我们支付的价格决定了代码字的长度。 码字的长度决定了它增加消息平均长度的多少。 我们可以这样想象他们。
短码字减少了平均消息长度，但是很昂贵，而长码字增加了平均消息长度，但是很便宜。
使用有限预算的最佳方法是什么？ 每个事件我们应在代码字上花费多少？
正如一个人想对他经常使用的工具进行更多的投资一样，我们也想在常用的代码字上花费更多。 有一种特别自然的方法：按照事件发生的频率分配预算。 因此，如果事件在50％的情况下发生，我们将花费预算的50％为其购买一个短代码字。 但是，如果事件仅在1％的时间发生，则我们仅花费预算的1％，因为我们并不十分担心代码字的长度。
这是很自然的事情，但这是否是最佳选择？ 是这样，我将证明这一点！
以下证据很清楚，应该理解，但这需要一些工作才能完成，这绝对是本文中最难的部分。 读者可以放心地跳过它，接受没有证据的事实，然后继续进行下一部分。让我们看一个特定的示例，在该示例中我们需要确定发生了两个可能的事件中的哪一个。大事记 和
。
成本和长度的界限很漂亮。那有什么意思吗？如果我们稍微改变码字的长度，请考虑一下成本和长度贡献的变化。如果我们稍微增加码字的长度，则消息长度的贡献将与它在边界处的高度成比例地增加，而成本将与它在边界处的高度成比例地降低。
因此，创建较短代码字的成本为 。
我们对每个代码字的长度并不同样担心；它们与我们使用频率的比例成比例。如果是 。
我们使代码字缩短一点的收益是成比例的 。
有趣的是，两个导数是相同的。这意味着我们的初始预算具有一个有趣的功能：如果您有更多的钱，那么投资减少任何代码字同样会很好。我们真正关心的是收益/成本比-这是决定我们应该在哪些方面进行更多投资的原因。在这种情况下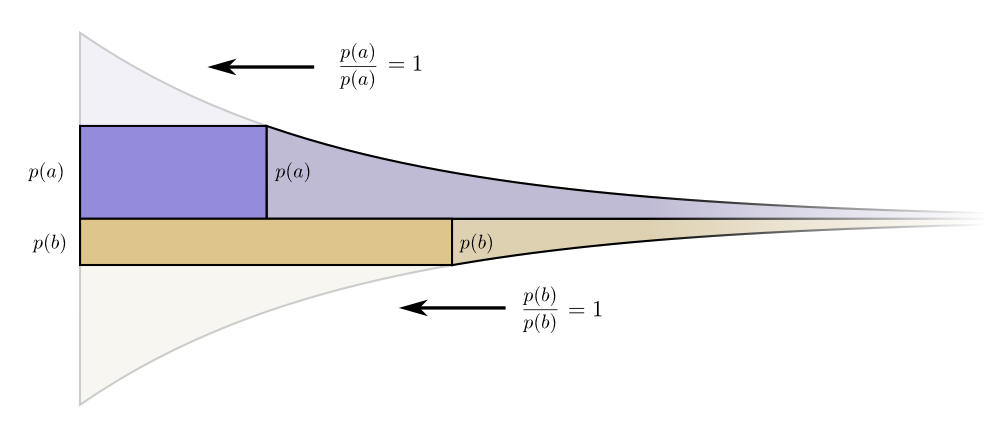
。
它为 。
但是好处是一样的。这导致以下事实：购买的成本/收益比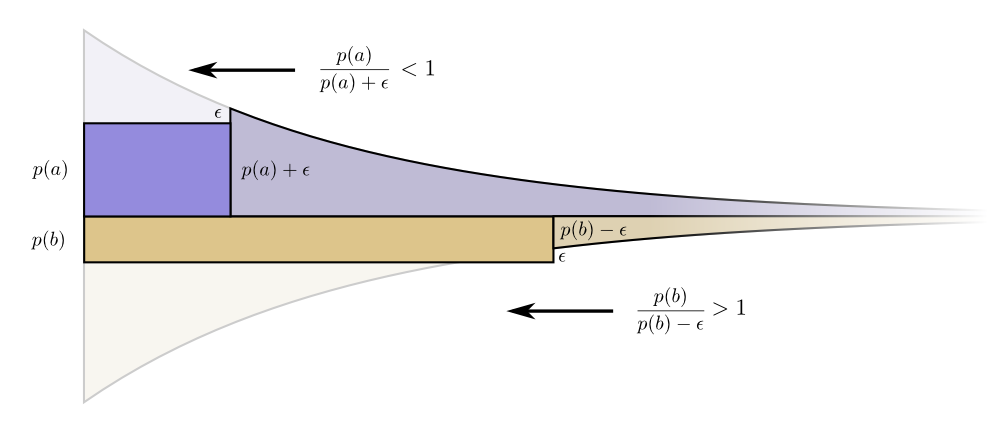
。
投资者高喊：“买入 ！
卖出 ( , , , , . ? , , , . , , , !)
PS , -, , .