如果您在keras.io网站上阅读了有关自动编码器的培训,则其中第一条消息是这样的:在实践中,几乎从未使用过自动编码器,但是在培训中经常会谈论自动编码器,并且有人来了,所以我们决定编写自己的关于它们的教程:
他们的成名主要来自许多在线提供的机器学习入门课程。 结果,该领域的许多新手绝对喜欢自动编码器,但购买力不足。 这就是本教程存在的原因!
但是,可以将其应用于自己的实际任务之一是查找异常,我个人在夜间项目的框架中需要它。
在互联网上,有很多关于自动编码器的教程,还有什么要写的呢? 好吧,说实话,有以下几个原因:
- 感觉实际上这些教程大约是3或4个,其余所有都是用自己的文字重写的;
- 几乎所有内容-在饱受苦难的MNIST'e上,图像尺寸为28x28;
- 以我的拙见,他们对所有这些工作方式没有直觉,而只是愿意重复一遍。
- 最重要的因素-就个人而言,当我用自己的数据集替换MNIST时-所有这些都愚蠢地停止了工作 。
下面描述了我塞满锥体的路径。 如果您从大量教程中采用任何建议的平面(非卷积)模型并愚蠢地将其粘贴,那么令人惊讶的是,没有任何事情不起作用。 本文的目的是理解原因,在我看来,这是对所有这些工作原理的某种直观理解。
我不是机器学习专家,而是在日常工作中使用惯用的方法。 对于经验丰富的数据科学家来说,整篇文章可能都是荒谬的,但是对初学者而言,在我看来,可能会有新的东西出现。
什么样的项目简而言之,尽管文章与他无关。 有一个ADS-B接收器,它从飞行中的飞机上捕获数据,并将飞机的坐标写入基地。 有时,飞机的行为举止不正常-降落前它们会转圈燃烧燃料,或者只是私人航班飞越标准路线(走廊)。 有趣的是,每天要从大约一千架飞机中分离出那些表现不佳的飞机。 我完全承认基本偏差可以轻松计算,但是我很想尝试一下 魔术 神经网络。
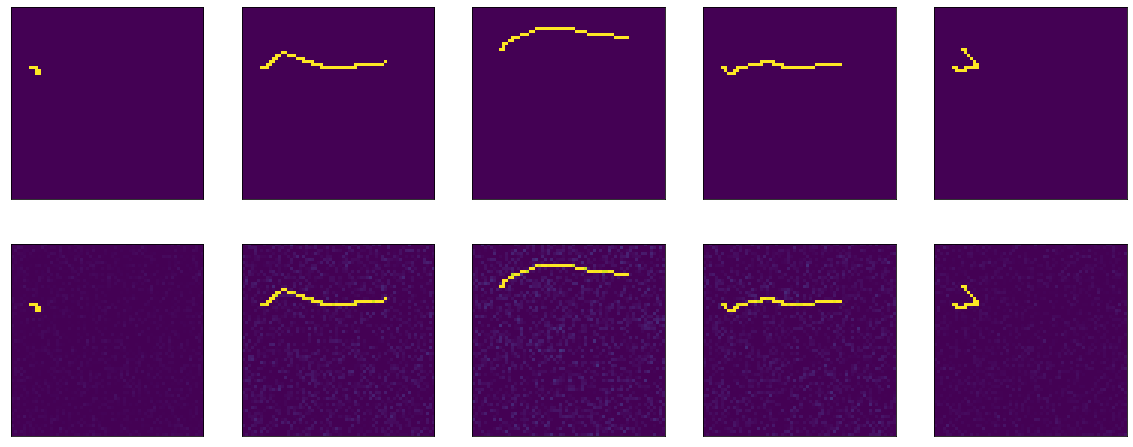
让我们开始吧。 我有4000张黑白图片的64x64像素数据集,看起来像这样:

黑色背景上只有几行,在64x64图片中,大约2%的点被填充。 当然,如果您查看许多图片,那么事实证明大多数线条都非常相似。
我不会详细介绍如何加载和处理数据集,因为同样,本文的目的不是这样。 只是显示一段可怕的代码。
例如,这里是keras.io提出的第一个模型,他们研究了mnist并对其进行了训练:
就我而言,模型的定义如下:
model = tf.keras.Sequential() model.add(tf.keras.Input(shape=(64,64,1))) model.add(tf.keras.layers.Flatten()) model.add(tf.keras.layers.Dense(64*64/10, activation='relu')) model.add(tf.keras.layers.Dense(64*64, activation="sigmoid")) model.add(tf.keras.layers.Reshape(target_shape=(64,64,1)))
我确实直接在模型中进行了展平和重塑,并且我没有“压缩” 25次,而仅压缩了10次,这之间存在细微的差异。这应该不会有任何影响。
作为损失函数-均方误差,优化器不是基本的,让亚当。 在下文中,我们训练20个时代,每个时代100步。
如果您查看指标-一切都在火中。 准确度== 0.993。 如果您看一下培训时间表,那么一切都会有些不愉快,我们到达了第三个时代的高原。
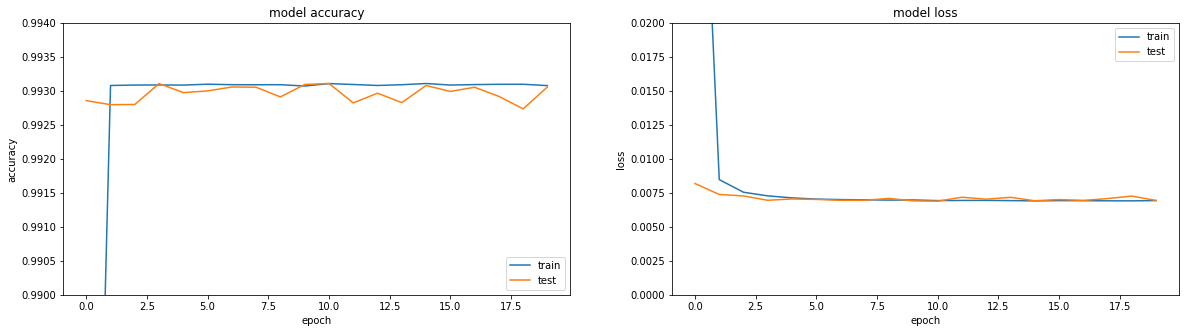
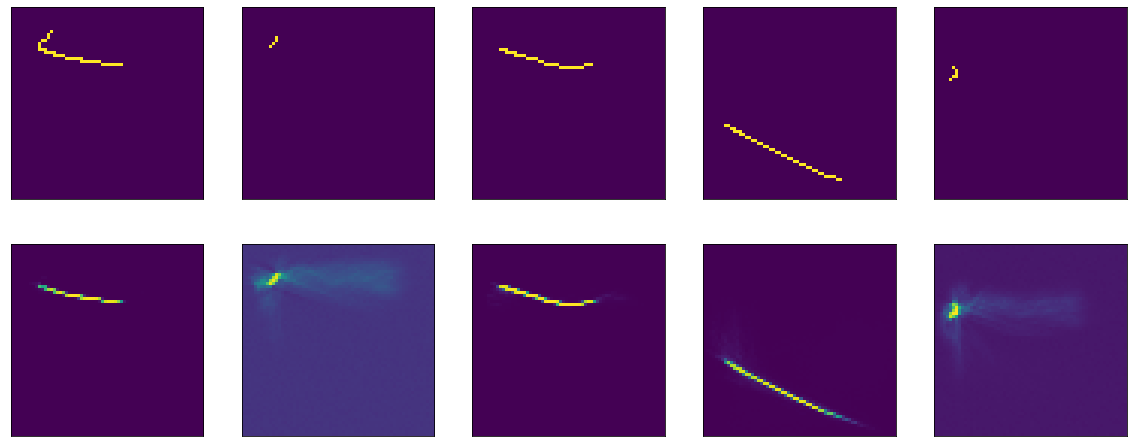
好吧,如果您直接看一下编码器的结果,您会得到一幅通常令人难过的图片(原始图片在最上面,而encoding-decoding的结果在下面):

通常,当您试图找出某项功能无法正常工作的原因时,这是一种将所有功能分解为大块并单独检查每个功能的好方法。 因此,让我们开始吧。
在本教程的原始篇中,将平面数据提供给模型输入,并在输出中获取它们。 为什么不检查我的展平和整形动作。 这是一个无操作模型:
model = tf.keras.Sequential() model.add(tf.keras.Input(shape=(64,64,1))) model.add(tf.keras.layers.Flatten()) model.add(tf.keras.layers.Reshape(target_shape=(64,64,1)))
结果:
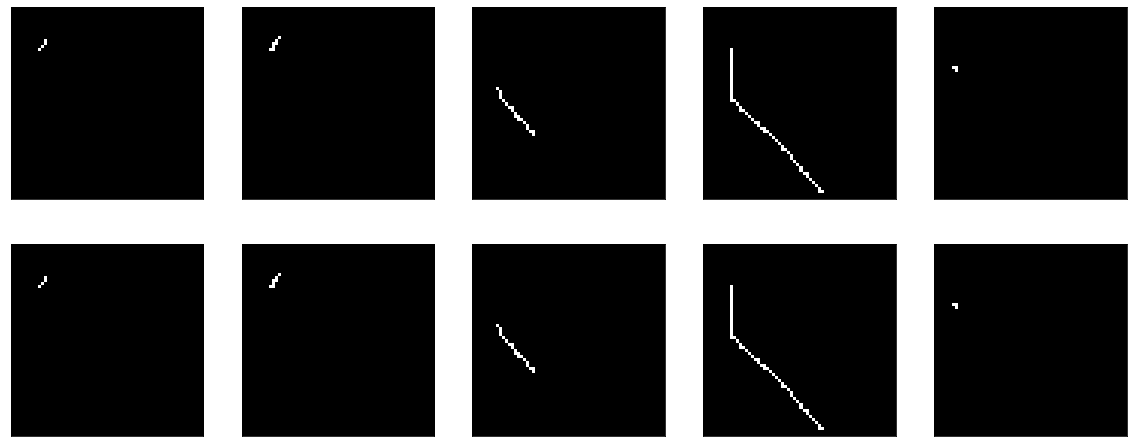
这里没有什么要教的。 好吧,与此同时,它证明了我的可视化功能也可以正常工作。
接下来,尝试使模型不是无操作的,而是尽可能哑巴的-剪掉压缩层,保留输入大小的一层。 正如他们在所有教程中所说的那样,模型学习功能而不只是身份功能非常重要。 好吧,这正是我们将要尝试得到的,让我们将生成的图片传递给输出即可。
model = tf.keras.Sequential() model.add(tf.keras.Input(shape=(64,64,1))) model.add(tf.keras.layers.Flatten()) model.add(tf.keras.layers.Dense(64*64, activation="sigmoid")) model.add(tf.keras.layers.Reshape(target_shape=(64,64,1)))
她正在学习一些东西,准确性== 0.995,然后她又跌跌撞撞地陷入了平稳状态。
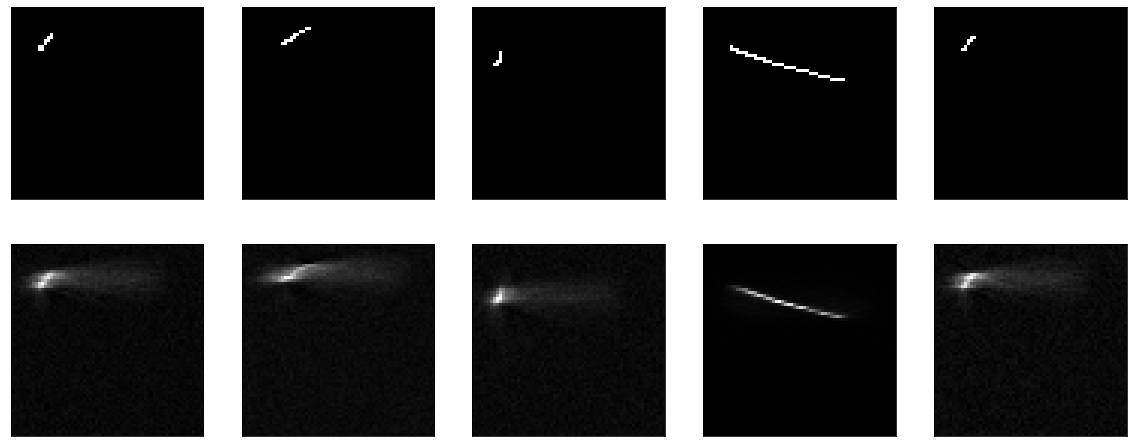
但是,总的来说,显然效果并不理想。 无论如何-在那儿学习什么,将入口传递到出口,仅此而已。
如果您阅读有关密集层的keras文档,它描述了它们的作用: output = activation(dot(input, kernel) + bias)
为了使输出与输入一致,两个简单的条件就足够了:bias = 0和内核-单位矩阵(重要的是不要在此处用单位填充矩阵-这是非常不同的东西)。 幸运的是,从同一个Dense的文档中可以很容易地做到这一点。
model = tf.keras.Sequential() model.add(tf.keras.Input(shape=(64,64,1))) model.add(tf.keras.layers.Flatten()) model.add(tf.keras.layers.Dense(64*64, activation = "sigmoid", use_bias=False, kernel_initializer = tf.keras.initializers.Identity())) model.add(tf.keras.layers.Reshape(target_shape=(64,64,1)))
因为 我们立即设置权重,那么您什么也学不到-马上就好了:
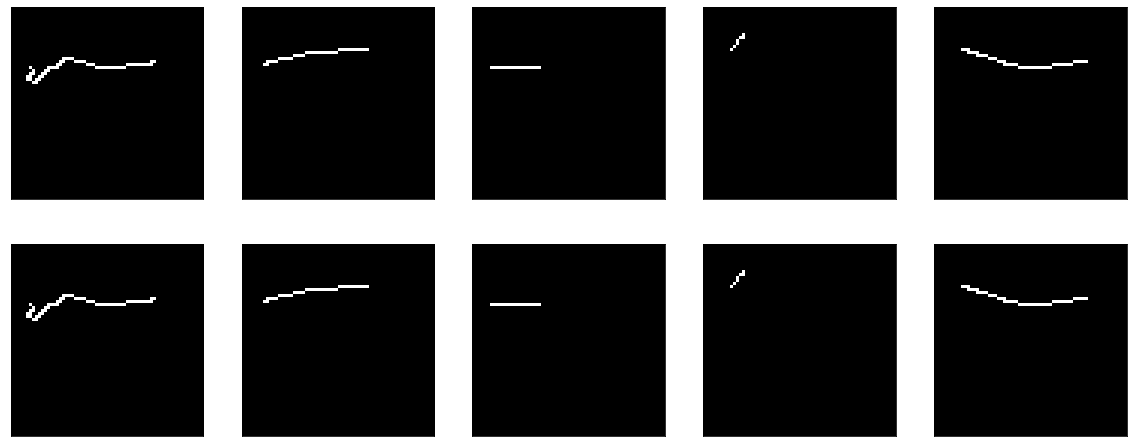
但是,如果您开始训练,那么乍看之下它会令人惊讶地开始-模型以精度== 1.0开始,但是很快就下降了。
训练前评估结果: 8/Unknown - 1s 140ms/step - loss: 0.2488 - accuracy: 1.0000[0.24875330179929733, 1.0] 。 培训内容:
Epoch 1/20 100/100 [==============================] - 6s 56ms/step - loss: 0.1589 - accuracy: 0.9990 - val_loss: 0.0944 - val_accuracy: 0.9967 Epoch 2/20 100/100 [==============================] - 5s 51ms/step - loss: 0.0836 - accuracy: 0.9964 - val_loss: 0.0624 - val_accuracy: 0.9958 Epoch 3/20 100/100 [==============================] - 5s 50ms/step - loss: 0.0633 - accuracy: 0.9961 - val_loss: 0.0470 - val_accuracy: 0.9958 Epoch 4/20 100/100 [==============================] - 5s 48ms/step - loss: 0.0520 - accuracy: 0.9961 - val_loss: 0.0423 - val_accuracy: 0.9961 Epoch 5/20 100/100 [==============================] - 5s 48ms/step - loss: 0.0457 - accuracy: 0.9962 - val_loss: 0.0357 - val_accuracy: 0.9962
是的,还不是很清楚,我们已经有了一个理想的模型-图片以1比1的比例出现,而损耗(均方误差)几乎为0.25。
顺便说一句,这是论坛上的一个常见问题-损失在下降,但准确性没有增长,这怎么可能?
这里值得再次回顾一下密集层的定义: output = activation(dot(input, kernel) + bias)和其中提到的激活一词,我在上面已经成功地忽略了它们。 有了来自单位矩阵的权重并且没有偏差,我们得到output = activation(input) 。
实际上,我们的源代码中的激活功能已经显示为sigmoid,我非常愚蠢地复制了它,仅此而已。 并且在教程中建议在任何地方使用它。 但是你必须弄清楚。
对于初学者,您可以阅读文档中有关其内容的内容: The sigmoid activation: (1.0 / (1.0 + exp(-x))) 。 那个人什么也没告诉我,因为我不是幻象大师,曾经在脑海中建立这样的图表。
但是您可以使用笔进行构建:
import matplotlib.ticker as plticker range_tensor = tf.range(-4, 4, 0.01, dtype=tf.float32) fig, ax = plt.subplots(1,1) plt.plot(range_tensor.numpy(), tf.keras.activations.sigmoid(range_tensor).numpy()) ax.grid(which='major', linestyle='-', linewidth='0.5', color='red') ax.grid(which='minor', linestyle=':', linewidth='0.5', color='black') ax.yaxis.set_major_locator(plticker.MultipleLocator(base=0.5) ) plt.minorticks_on()
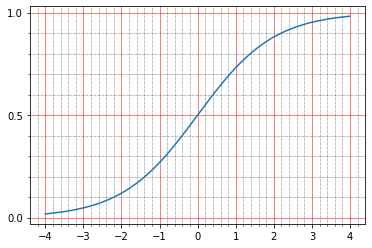
从这里可以清楚地看到,S形为零时,S形为0.5,单位为0.73。 我们得到的点是黑色(0.0)或白色(1.0)。 因此事实证明,恒等函数的均方误差保持非零。
您甚至可以看一下笔,这是所得图像的一行:
array([0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.7310586, 0.7310586, 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 , 0.5 ], dtype=float32)
实际上,这很酷,因为会同时出现几个问题:
- 为什么在上面的可视化图中看不到它?
- 为什么那么精度== 1.0,因为原始图片是0和1。
通过可视化,一切都非常简单。 为了显示图像,我使用了matplotlib: plt.imshow(res_imgs[i][:, :, 0]) 。 而且,像往常一样,如果您转至文档,一切都将写在此处: The Normalize instance used to scale scalar data to the [0, 1] range before mapping to colors using cmap. By default, a linear scaling mapping the lowest value to 0 and the highest to 1 is used. The Normalize instance used to scale scalar data to the [0, 1] range before mapping to colors using cmap. By default, a linear scaling mapping the lowest value to 0 and the highest to 1 is used. 即 库仔细地将我的0.5和0.73标准化为0到1。更改代码:
plt.imshow(res_imgs[i][:, :, 0], norm=matplotlib.colors.Normalize(0.0, 1.0))

这是准确的问题。 首先-出于习惯,我们去了文档,阅读tf.keras.metrics.Accuracy ,看起来它们写得可以理解:
For example, if y_true is [1, 2, 3, 4] and y_pred is [0, 2, 3, 4] then the accuracy is 3/4 or .75.
但是在这种情况下,我们的准确度应该为0。因此,我将自己埋在了源代码中,这对我自己很清楚:
When you pass the strings 'accuracy' or 'acc', we convert this to one of `tf.keras.metrics.BinaryAccuracy`, `tf.keras.metrics.CategoricalAccuracy`, `tf.keras.metrics.SparseCategoricalAccuracy` based on the loss function used and the model output shape. We do a similar conversion for the strings 'crossentropy' and 'ce' as well.
而且,由于某种原因,在本网站的文档中,该段落不在.compile的描述中。
这是来自https://github.com/tensorflow/tensorflow/blob/66c48046f169f3565d12e5fea263f6d731f9bfd2/tensorflow/python/keras/engine/compile_utils.py的一段代码
y_t_rank = len(y_t.shape.as_list()) y_p_rank = len(y_p.shape.as_list()) y_t_last_dim = y_t.shape.as_list()[-1] y_p_last_dim = y_p.shape.as_list()[-1] is_binary = y_p_last_dim == 1 is_sparse_categorical = ( y_t_rank < y_p_rank or y_t_last_dim == 1 and y_p_last_dim > 1) if metric in ['accuracy', 'acc']: if is_binary: metric_obj = metrics_mod.binary_accuracy elif is_sparse_categorical: metric_obj = metrics_mod.sparse_categorical_accuracy else: metric_obj = metrics_mod.categorical_accuracy
y_t是y_true,或者是预期输出, y_p是y_predicted,或者是预测结果。
我们具有以下数据格式: shape=(64,64,1) ,因此事实证明,精度被视为binary_accuracy。 为了如何考虑利益:
def binary_accuracy(y_true, y_pred, threshold=0.5): threshold = math_ops.cast(threshold, y_pred.dtype) y_pred = math_ops.cast(y_pred > threshold, y_pred.dtype) return K.mean(math_ops.equal(y_true, y_pred), axis=-1)
有趣的是,在这里我们很幸运-默认情况下,所有东西都被视为大于0.5且小于等于0.5的单位-零。 因此,对于我们的身份模型而言,准确性达到了百分之一百,尽管实际上数字根本不尽相同。 好吧,很明显,如果我们确实愿意的话,那么我们可以校正阈值并将精度降低为零,例如,仅不需要它。 这是一个指标,不会影响培训,您只需要了解您可以用一千种不同的方式进行计算并获得完全不同的指标即可。 举例来说,您可以使用笔提取各种指标并将我们的数据传输给它们:
m = tf.keras.metrics.BinaryAccuracy() m.update_state(x_batch, res_imgs) print(m.result().numpy())
将给我们1.0 。
在这里
m = tf.keras.metrics.Accuracy() m.update_state(x_batch, res_imgs) print(m.result().numpy())
在相同数据上将给我们0.0 。
顺便说一下,可以使用同一段代码来处理损失函数并了解其工作原理。 如果您阅读了有关自动编码器的教程,则基本上他们建议使用两个损失函数之一:均方误差或'binary_crossentropy'。 您也可以同时查看它们。
我提醒您,对于mse我已经提供了evaluate模型:
8/Unknown - 2s 221ms/step - loss: 0.2488 - accuracy: 1.0000[0.24876083992421627, 1.0]
即 损失== 0.2488。 让我们看看为什么会这样。 在我个人看来,这是最简单,最容易理解的:y_true和y_predict之间的差异逐像素相减,每个结果均平方,然后搜索平均值。
tf.keras.backend.mean(tf.math.squared_difference(x_batch[0], res_imgs[0]))
并在输出:
<tf.Tensor: shape=(), dtype=float32, numpy=0.24826494>
这里的直觉非常简单-大多数空白像素,模型产生0.5,它们得到0.25-平方差。
使用二元交叉中心法,事情会稍微复杂一些,并且有整篇文章介绍了它是如何工作的,但是就我个人而言,我总是更容易阅读源代码,并且看起来像这样:
if from_logits: return nn.sigmoid_cross_entropy_with_logits(labels=target, logits=output) if not isinstance(output, (ops.EagerTensor, variables_module.Variable)): output = _backtrack_identity(output) if output.op.type == 'Sigmoid':
老实说,我花了很长时间在这几行代码上绞尽脑汁。 首先,很明显,两个实现可以起作用:要么sigmoid_cross_entropy_with_logits ,要么最后一行对起作用。 区别在于sigmoid_cross_entropy_with_logits可用于logits(顾名思义,就是doh),而主代码则可用于概率。
谁是登录用户? 如果您阅读了有关该主题的100万篇不同文章,那么他们将提到数学定义,公式等。 实际上,一切似乎都非常简单(如果我错了,请纠正我)。 预测的原始输出为logits。 好吧,或者说对数奇数,是用对数鹦鹉计算的对数赔率。
题外话很小-为什么会有对数赔率是我们需要的事件数与我们不需要的事件数之比(与概率相反,概率是我们需要的事件与总的所有事件数之比)。 例如-我们队的胜利数到失败的数。 还有一个问题。 继续以团队的胜利为榜样,我们的团队可以是输家,并且有机会赢得1/2(一到两),甚至有可能是输家,并且有机会赢得1/100。 方向相反-中陡,比最高山高2/1,然后是100/1。 事实证明,失败者团队的整个范围由0到1的数字以及从1到无穷的酷团队描述。 结果,比较起来很不方便,没有对称性,一般来说用它来工作对每个人都是不方便的,数学出来的丑陋。 如果您采用对数的对数,那么一切都会变得对称:
ln(1/2) == -0.69 ln(2/1) == 0.69 ln(1/100) == -4.6 ln(100/1) == 4.6
在张量流的情况下,这是任意的,因为严格来说,该层的输出在数学上不是对数奇数,而是已经被接受。 如果原始值是从-∞到+∞-,则进行logits。 然后可以将它们转换为概率。 有两个选项:softmax及其特殊情况Sigmoid。 Softmax-取一个logit向量,并将其转换为一个概率向量,甚至使其中所有事件的概率总和变为1。Sigmoid(在tf的情况下)也取一个logits向量,但分别将其分别转换为概率从其余的。
您可以这样看。 有多标签分类任务,有多分类分类任务。 多类-这是如果您需要确定图片中的苹果或橙子,甚至是菠萝。 多标签是指图片中有一个水果花瓶,您需要说的是上面有苹果和橙子,但没有菠萝。 如果我们需要多类-我们需要softmax,如果我们需要multilabel-我们需要Sigmoid。
在这里,我们遇到了多标签的情况-每个像素(类)都必须说出是否已安装。
回到张量流,为什么在二元交叉熵(至少在其他交叉熵函数中几乎相同)中有两个全局分支。 交叉熵总是适用于概率,我们稍后再讨论。 然后有两种简单的方法:要么概率已经输入了输入,要么对数进入了输入-然后将sigmoid应用于它们以获得概率。 碰巧的是,应用Sigmoid和计算交叉熵要比仅从概率计算交叉熵更好(原因的数学输出在sigmoid_cross_entropy_with_logits函数的源中,加上出于好奇,您可以在Google上搜索“数值稳定性交叉熵”),因此即使张量流开发人员也建议不要将概率传递给输入交叉熵函数,并返回原始logit。 好吧,在代码中,检查了损失函数是否最后一层是Sigmoid,然后将其切断并取激活输入而不是其输出进行计算,并将所有要考虑的内容发送到sigmoid_cross_entropy_with_logits 。
好的,整理出来,现在是binary_crossentropy。 有两种流行的“直觉”解释可以衡量交叉熵。
更正式:假设有一个特定的模型,对于n个类,知道它们出现的概率(y 0 ,y 1 ,...,y n )。 现在在生活中,这些类别中的每一个都出现了k n次(k 1 ,k 1 ,...,k n )。 此类事件的概率是每个类别的概率的乘积-(y 1 ^ k 1 )(y 2 ^ k 2 )...(y n ^ k n )。 原则上-这已经是交叉熵的常规定义-一个数据集的概率用另一个数据集的概率表示。 此定义的问题在于它将变成0到1,并且通常很小;比较这些值并不方便。
如果我们从中取对数,则将得出k 1 log(y 1 )+ k 2 log(y 2 ),依此类推。 值的范围从-∞到0。所有这些都乘以-1 / n-,并且从0到+∞的范围也出现了,因为 它表示为每个类别的值之和,每个类别中的更改以非常可预测的方式反映在总体值中。
更简单:交叉熵显示就原始模型而言,需要多少额外的位来表达样本。 如果我们在那里以2为底进行对数,那么我们将直接进行位运算。 我们到处都使用自然对数,因此它们显示的是nat的数量( https://en.wikipedia.org/wiki/Nat_(unit )),而不是位数。
当类数为2时,二进制交叉熵又是普通交叉熵的一种特殊情况。 然后,我们对一个类别y 1的发生概率有了足够的了解,而第二个类别的发生概率为(1-y 1 )。
但是,在我看来,有点打滑了我。 让我提醒您,上一次我们尝试构建身份自动编码器时,他向我们展示了一张漂亮的图片,甚至达到了1.0的精度,但实际上,结果却是可怕的。 为了进行实验,您可以进行更多测试:
1)激活可以完全删除,会有干净的身份
2)您可以尝试其他激活功能,例如相同的relu
没有激活:
model = tf.keras.Sequential() model.add(tf.keras.Input(shape=(64,64,1))) model.add(tf.keras.layers.Flatten()) model.add(tf.keras.layers.Dense(64*64, use_bias=False, kernel_initializer=tf.keras.initializers.Identity())) model.add(tf.keras.layers.Reshape(target_shape=(64,64,1)))
我们得到了完美的身份模型:
model.evaluate(x=val.map(lambda x: (x,x)).batch(BATCH_SIZE, drop_remainder=True))
顺便说一句,训练不会导致任何结果,因为损失== 0.0。
现在有了relu。 他的图如下所示:
import matplotlib.ticker as plticker range_tensor = tf.range(-4, 4, 0.01, dtype=tf.float32) fig, ax = plt.subplots(1,1) plt.plot(range_tensor.numpy(), tf.keras.activations.relu(range_tensor).numpy()) ax.grid(which='major', linestyle='-', linewidth='0.5', color='red') ax.grid(which='minor', linestyle=':', linewidth='0.5', color='black') ax.yaxis.set_major_locator(plticker.MultipleLocator(base=1) ) plt.minorticks_on()
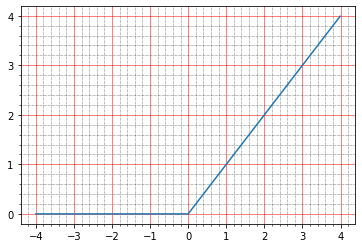
低于零-零,高于-y = x,即 从理论上讲,我们应该获得与没有激活时相同的效果-一个理想的模型。
model = tf.keras.Sequential() model.add(tf.keras.Input(shape=(64,64,1))) model.add(tf.keras.layers.Flatten()) model.add(tf.keras.layers.Dense(64*64, activation='relu', use_bias=False, kernel_initializer=tf.keras.initializers.Identity())) model.add(tf.keras.layers.Reshape(target_shape=(64,64,1))) model.compile(optimizer="adam", loss="binary_crossentropy", metrics=["accuracy"]) model.evaluate(x=val.map(lambda x: (x,x)).batch(BATCH_SIZE, drop_remainder=True))
好的,我们弄清楚了身份模型,即使理论的某些部分变得更加清晰。 现在让我们尝试训练相同的模型,使其成为身份。
为了好玩,我将对三个激活功能进行此实验。 首先-relu,因为它显示得很早(一切都和以前一样,但是kernel_initializer被删除了,所以默认情况下它将是glorot_uniform ):
model = tf.keras.Sequential() model.add(tf.keras.Input(shape=(64,64,1))) model.add(tf.keras.layers.Flatten()) model.add(tf.keras.layers.Dense(64*64, activation='relu', use_bias=False)) model.add(tf.keras.layers.Reshape(target_shape=(64,64,1)))
它学得很棒:
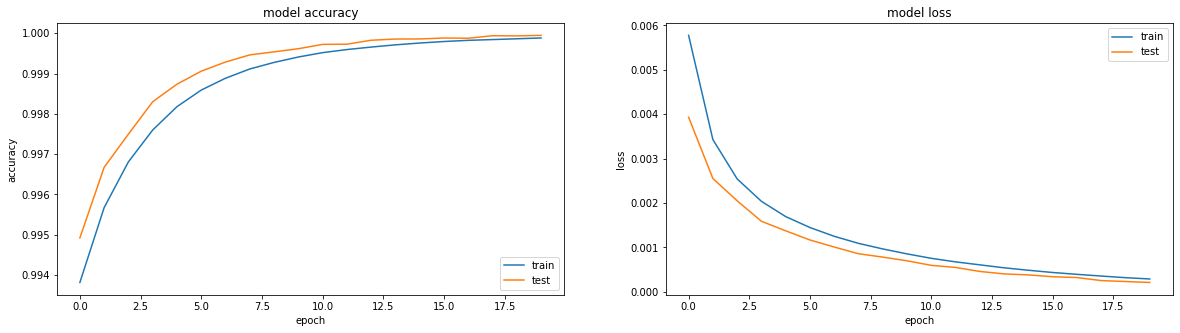
结果是相当不错的,准确性:0.9999,损失(毫秒):经过20个时代的2e-04,您可以进一步训练。

接下来,尝试使用sigmoid:
model = tf.keras.Sequential() model.add(tf.keras.Input(shape=(64,64,1))) model.add(tf.keras.layers.Flatten()) model.add(tf.keras.layers.Dense(64*64, activation='sigmoid', use_bias=False)) model.add(tf.keras.layers.Reshape(target_shape=(64,64,1)))
我之前已经教过类似的东西,唯一的区别是这里禁用了偏见。 他专心研究,在50年代进入了一个稳定的时代,准确性:0.9970,损失:60年代后的0.01。
结果再次令人印象深刻:
好吧,还要检查tanh:
model = tf.keras.Sequential() model.add(tf.keras.Input(shape=(64,64,1))) model.add(tf.keras.layers.Flatten()) model.add(tf.keras.layers.Dense(64*64, activation='tanh', use_bias=False)) model.add(tf.keras.layers.Reshape(target_shape=(64,64,1)))
其结果可与relu相提并论-精度:0.9999,损失:6e-04,经过20个时代之后,您可以进一步进行训练:

事实上,我是否为使乙状结肠显示出可比的结果而感到困扰。 完全出于体育兴趣。
例如,您可以尝试添加BatchNormalization:
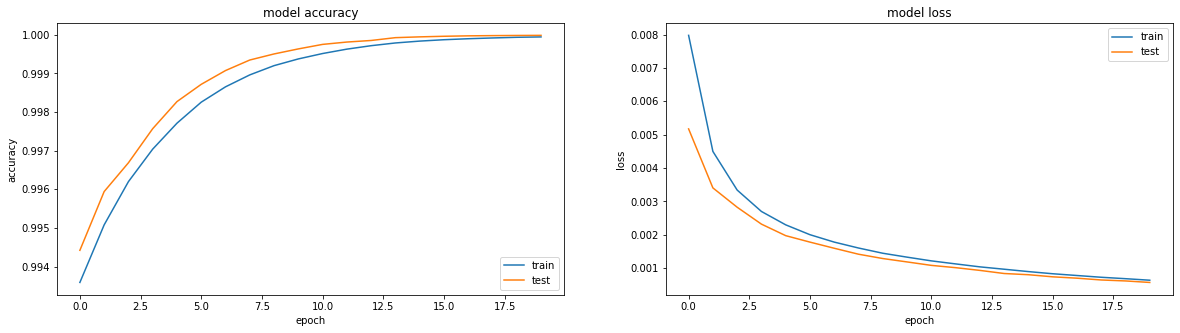
model = tf.keras.Sequential() model.add(tf.keras.Input(shape=(64,64,1))) model.add(tf.keras.layers.Flatten()) model.add(tf.keras.layers.Dense(64*64, activation='sigmoid', use_bias=False)) model.add(tf.keras.layers.BatchNormalization()) model.add(tf.keras.layers.Reshape(target_shape=(64,64,1)))
然后发生某种魔术。 在第13时代,准确性:1.0。 和火热的结果:
III ...在这个悬崖式衣架上,我将完成第一部分,因为文本太模糊,并且尚不清楚是否有人需要它。 在第二部分中,我将了解发生了什么魔术,尝试使用不同的优化器,尝试构建一个诚实的编码器-解码器,将我的头放在桌子上。 我希望有人对此感兴趣并有所帮助。